Merkle–Damgård是一种算法,由Ralph Merkle和Ivan Damgård提出。它通过迭代调用压缩函数来计算消息的哈希值。
应用
拿SHA-2举例,首先我们需要对需要进行哈希运算的输入做填充,然后将填充后的输入划分为等长的分组,每个分组的长度等于压缩函数的输入长度。填充的意思就是在输入中添加特定的字节,使输入的长度变成分组大小的整数倍。

然后,将压缩函数应用于消息的所有分组,在每次迭代过程中,都将上一轮的输出作为压缩函数的第二个输入参数,而将消息的某个分组作为它的第一个输入参数。将压缩函数最终的输出作为消息的摘要。

如果压缩函数本身是抗碰撞的,那么就可以证明Merkle–Damgård结构是抗碰撞的。这样一来,输入长度不固定的哈希函数的安全性就简化为输入长度固定的压缩函数的安全性。
构造
Merkle–Damgård结构的目标是从压缩函数构造一个哈希函数
:
给定任意长度的消息x,使得:
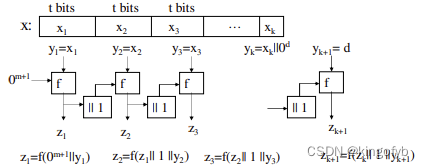
例子:
给定一个压缩函数f:
消息x有1000bits:
是x的前512bits
是
的后488bits
是24的
二进制表示
,
有128bits
,
是h(x)的消息摘要
抗碰撞性
为什么如果压缩函数本身是抗碰撞的,Merkle–Damgård结构就是抗碰撞的呢?
给定压缩函数和Merkle–Damgård结构
:
- 假设我们找到
所以h(x)
h(x'),所以
可以找到碰撞。
- 让
- 让h(x)的中间结果等于
,然后
- 让h(x')的中间结果等于
和
然后,
- 情况1:
(填充位的数量不同),然后
,发现碰撞
- 情况2:
然后k=n,要么
发现碰撞;要么
,
,如果
,发现碰撞;如果
,则发现碰撞,否则返回。一定有一个数字j使得
。
- 情况3:
,跟情况1相似,除了我们可以一直回到其中一个字符串的开头并且有
,碰撞被发现。