6.1.1图的基本概念

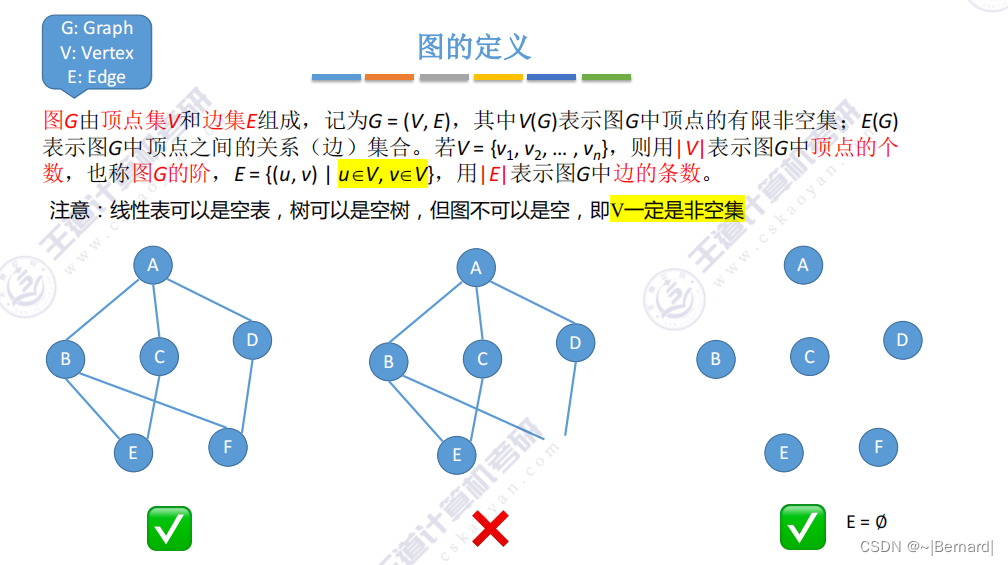
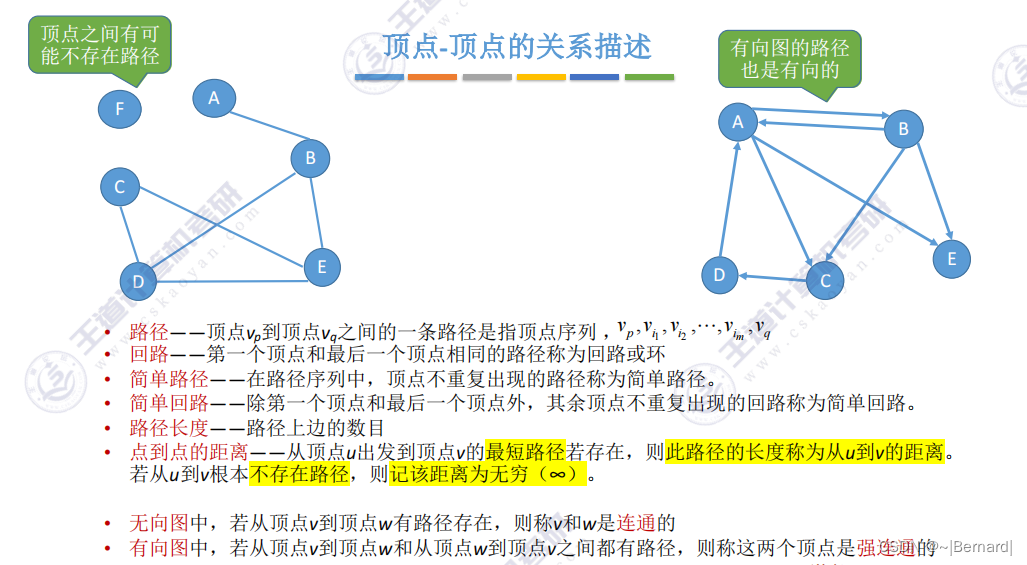
 顶点集一定是非空集，边集可以是空集

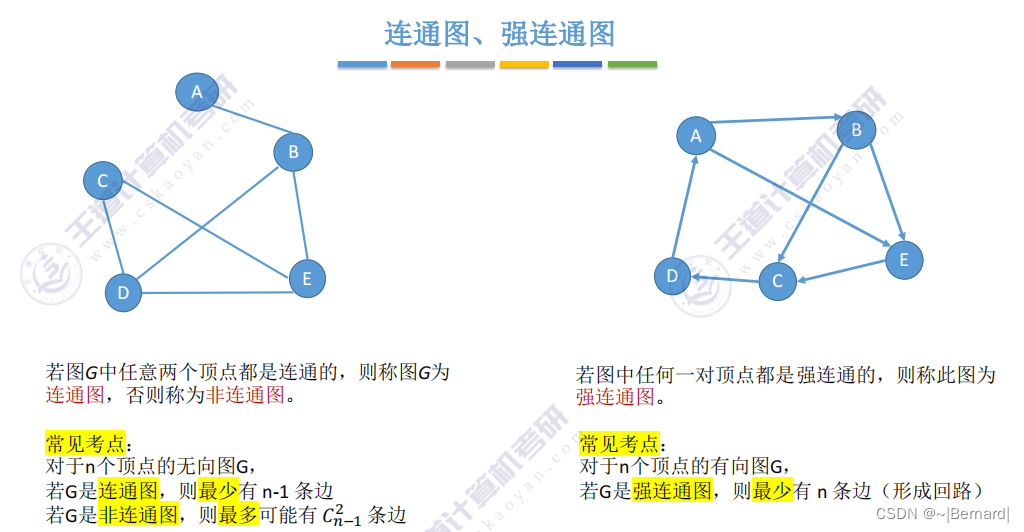
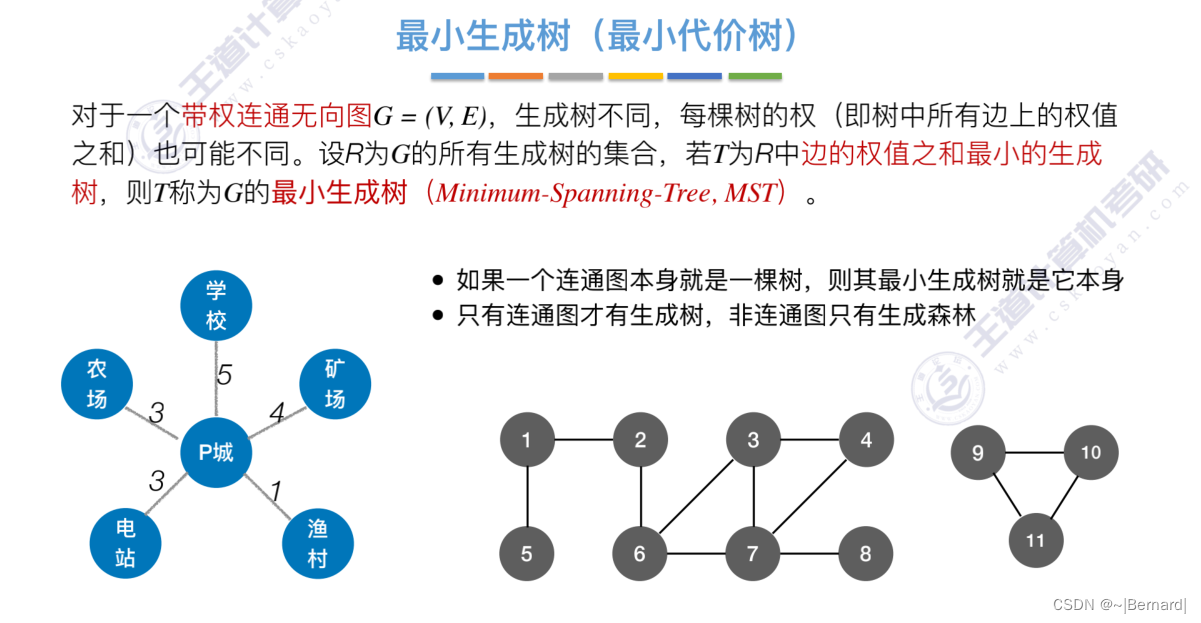
 非连通图：让任意n-1个顶点之间两两相连，另一个顶点与任意一个都不存在路径，则为非连通图的最大边数。

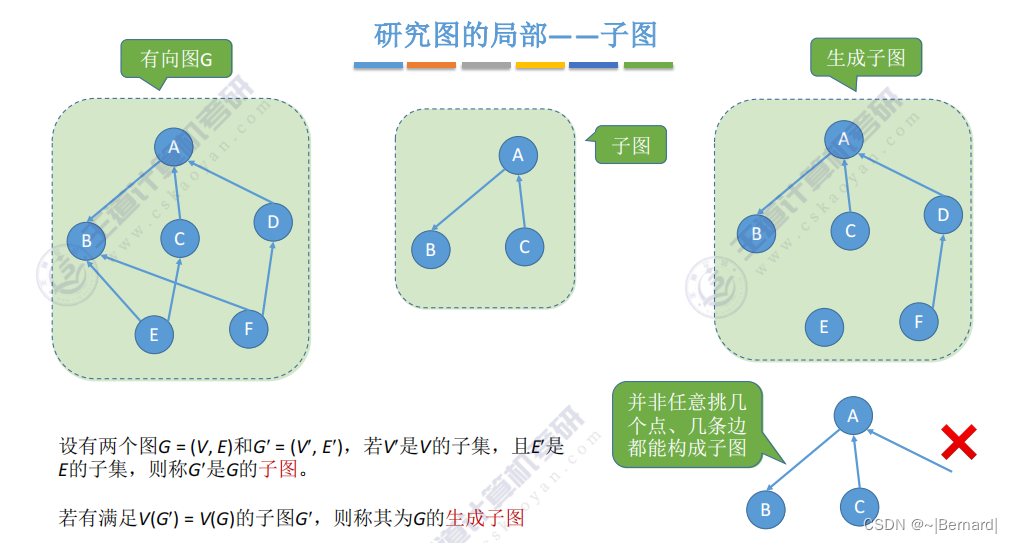
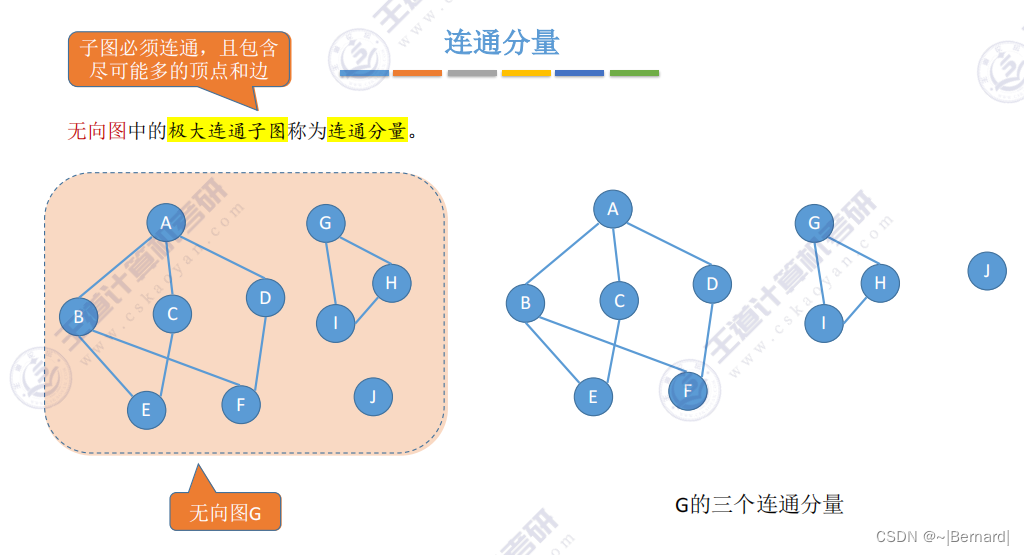
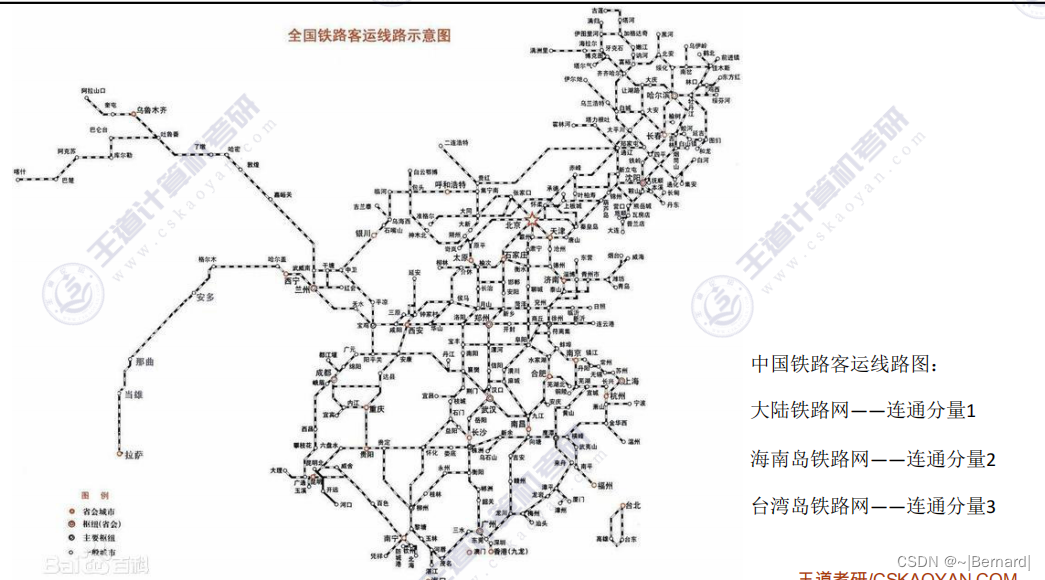
注意长三角地区铁路网不属于连通分量，因为它没有包含尽可能多的边和顶点，只有扩展到整个大路铁路网才是连通分量。

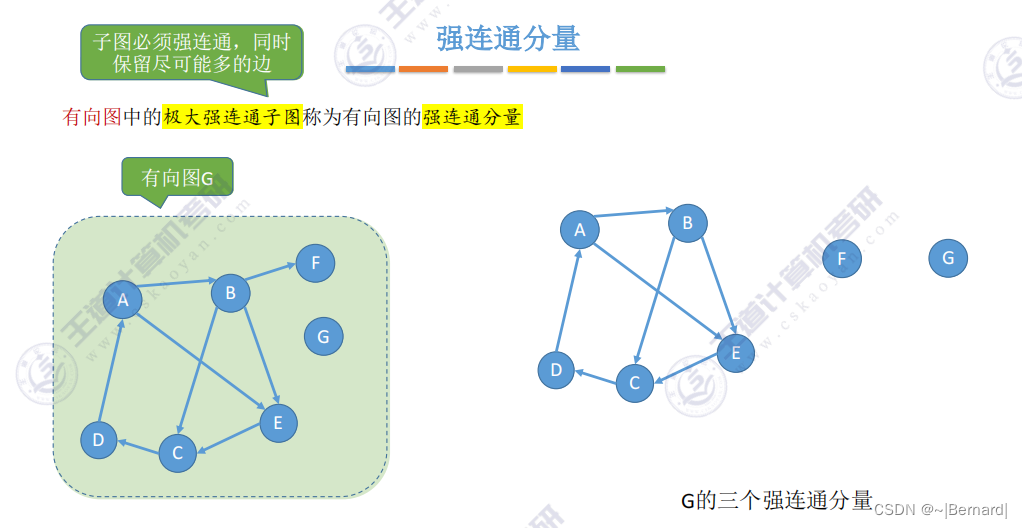
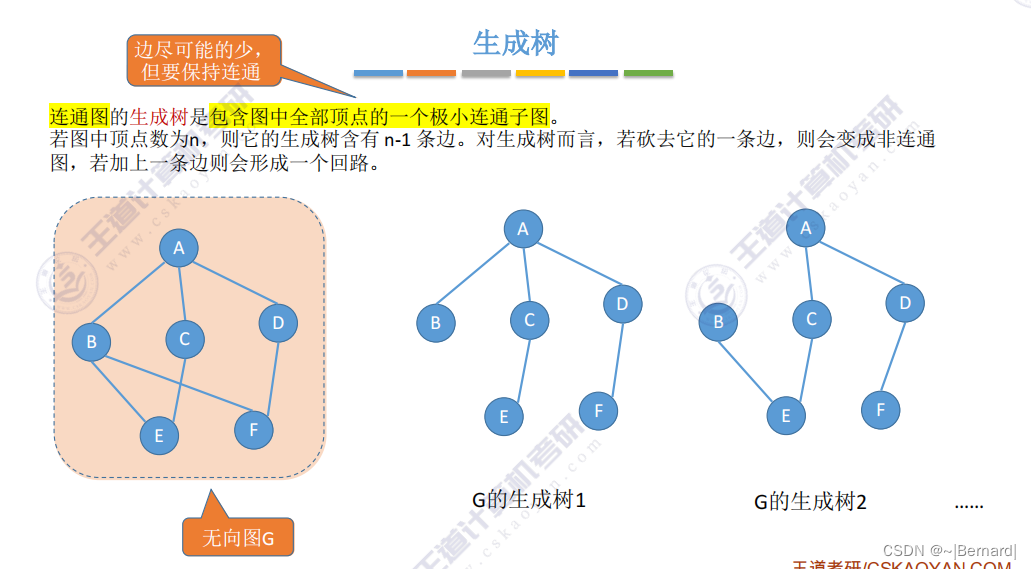
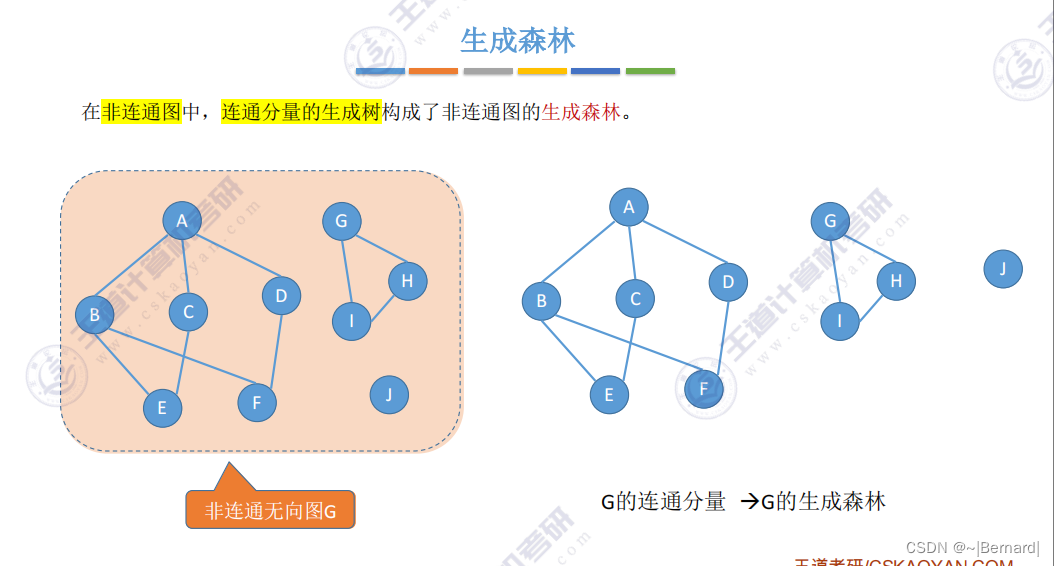
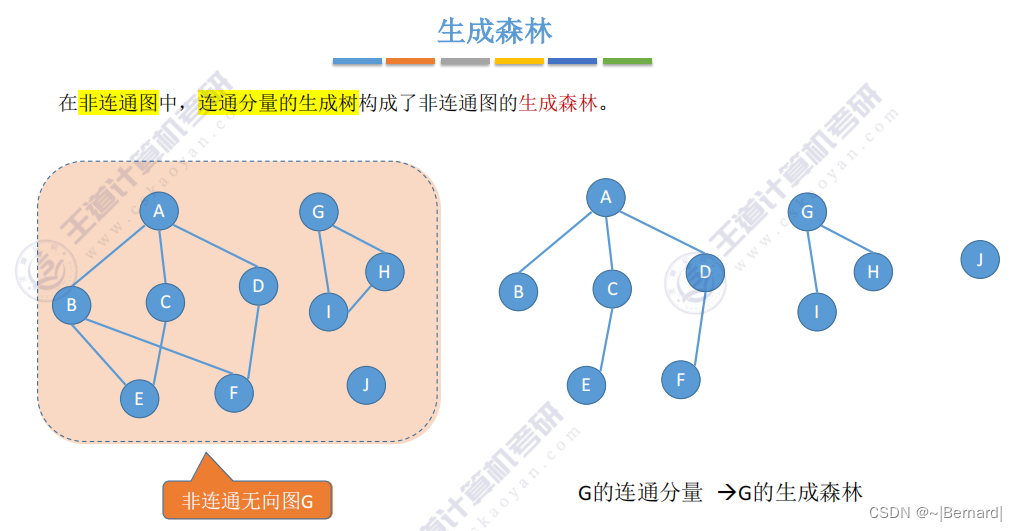
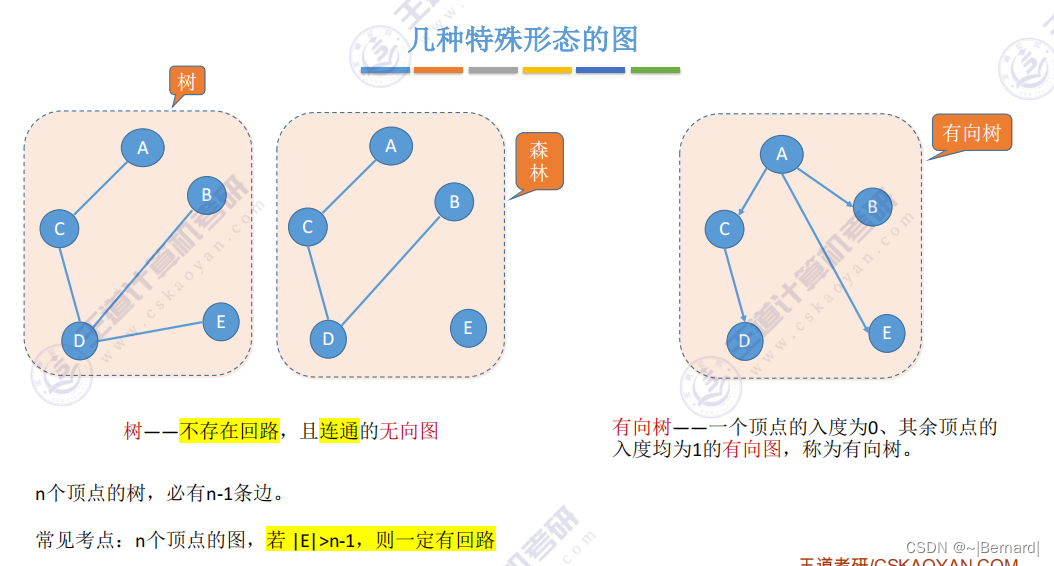
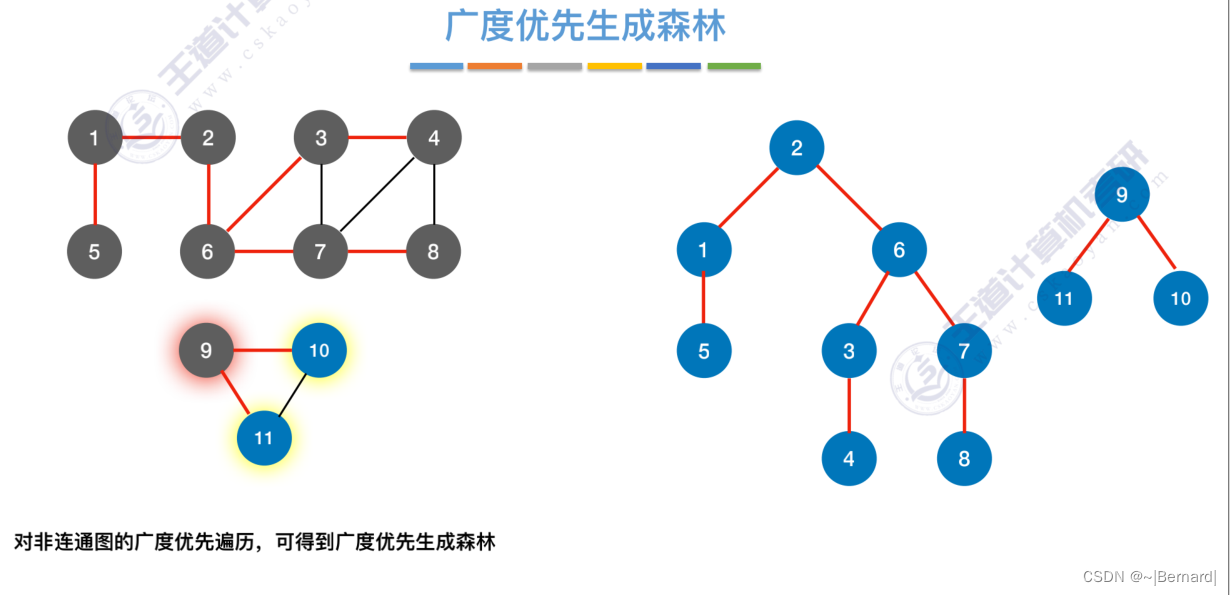
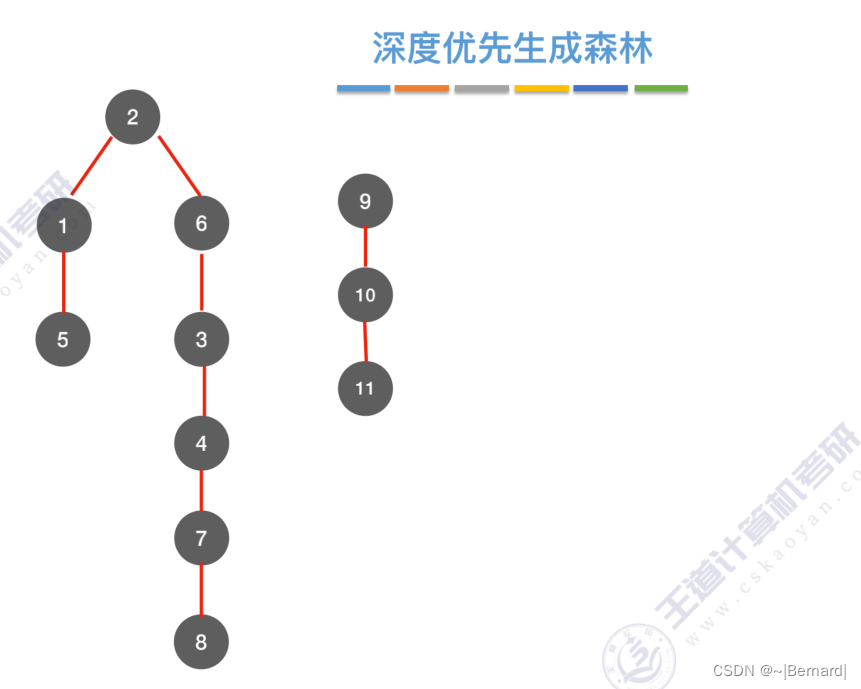
 把每一个连通分量生成与之对应的生成树，即可得到整个非连通图的生成森林。

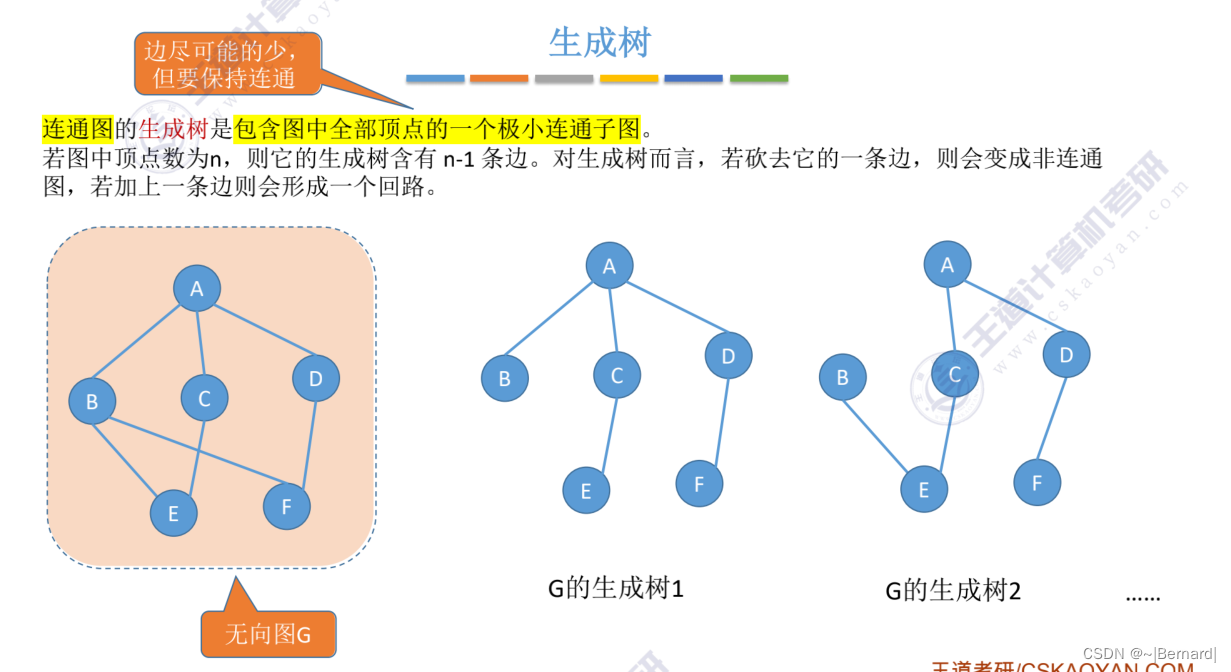
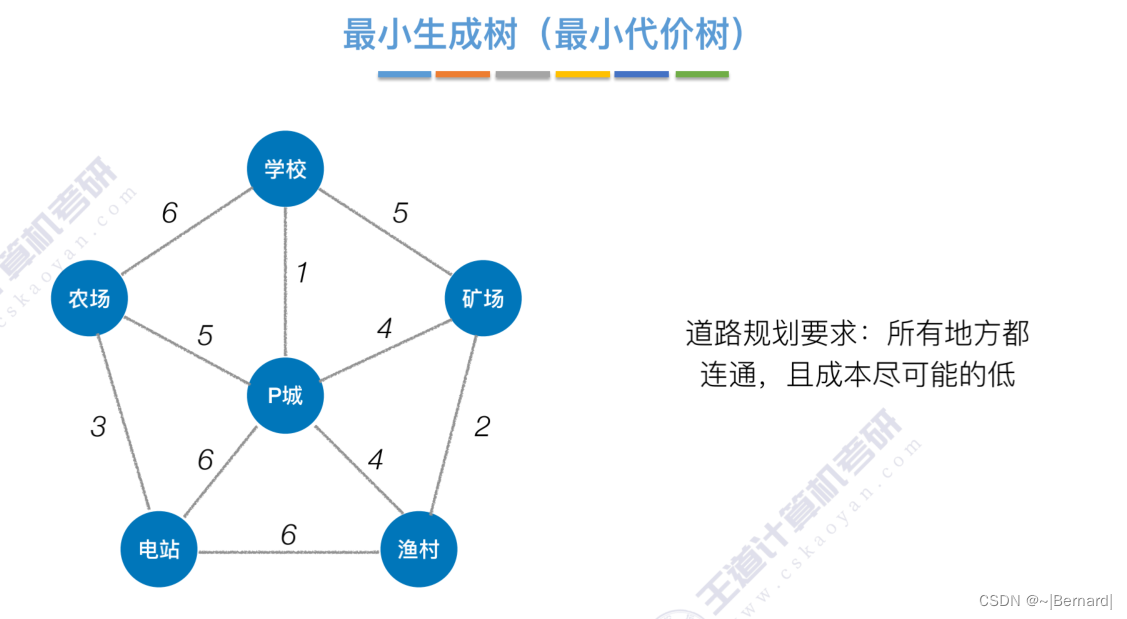
生成树具有很强的现实意义，如果几个村庄之间需要修公路，那么在所有的施工方案中需要去选择既可以连通所有村庄的路又可以减少修建成本的方案，即减少一些冗余边，就是极小连通子图.

 

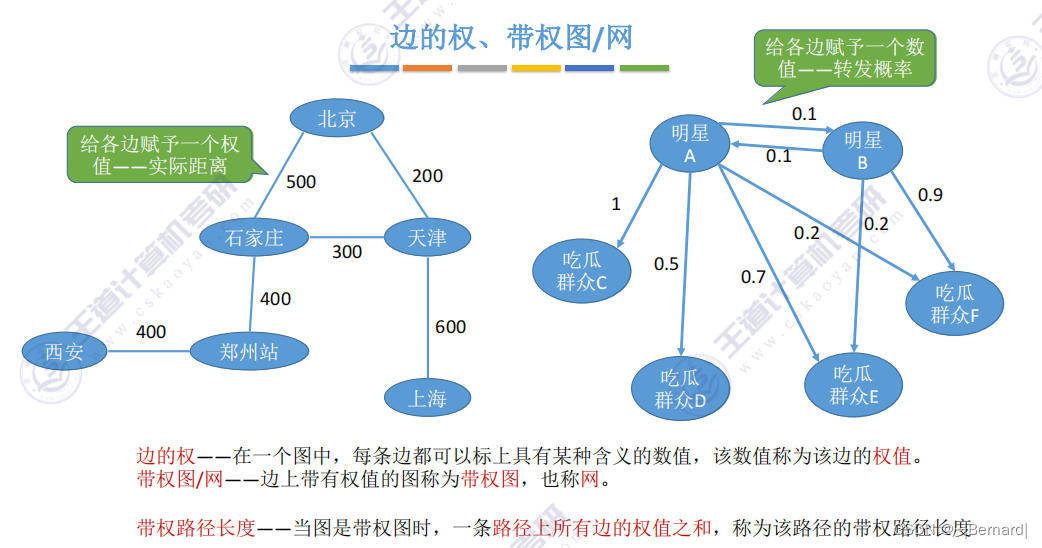
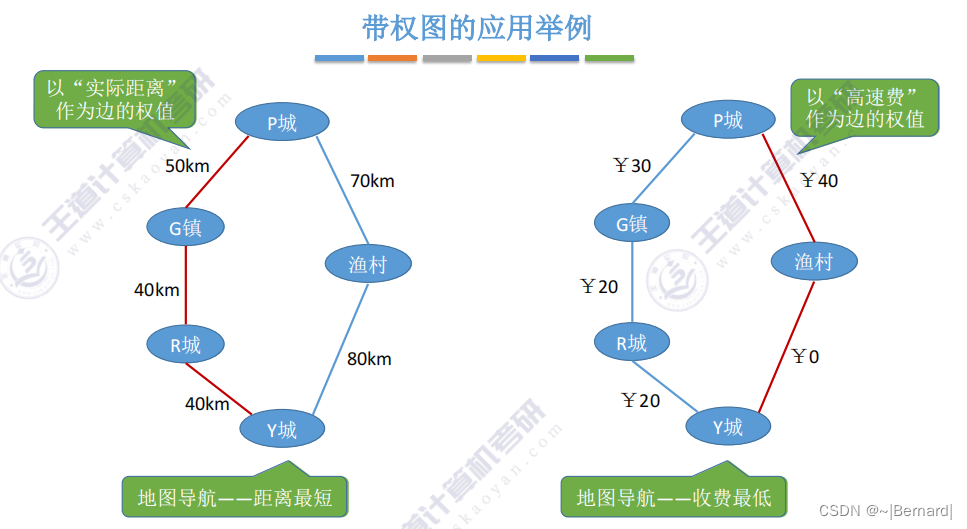
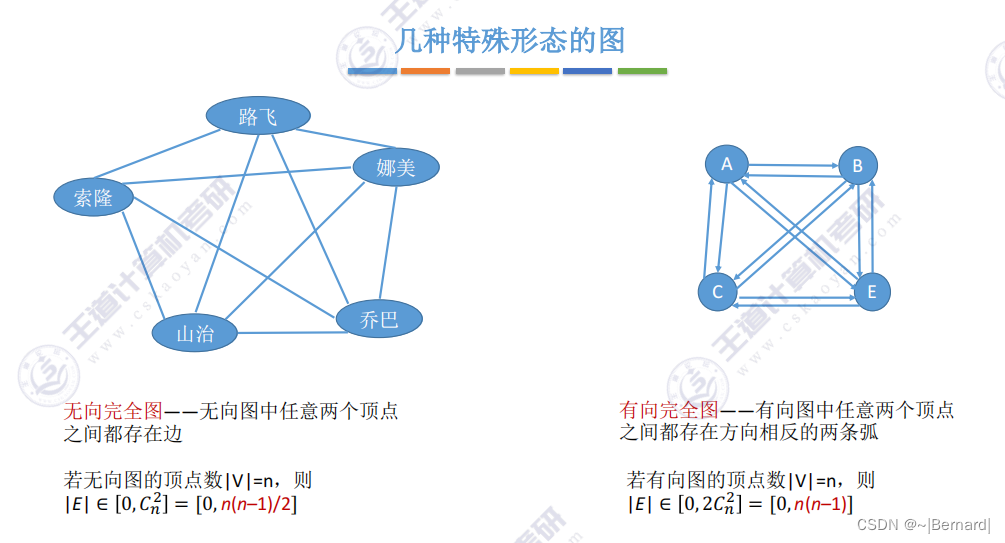
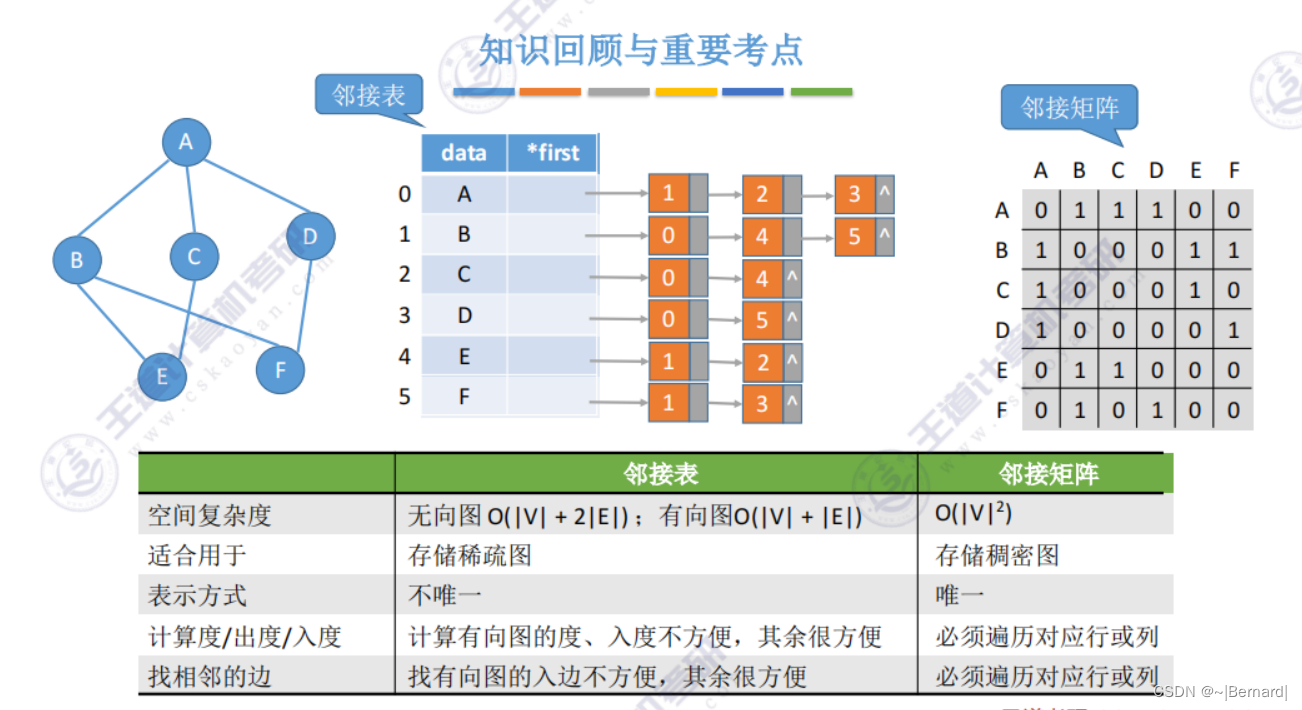
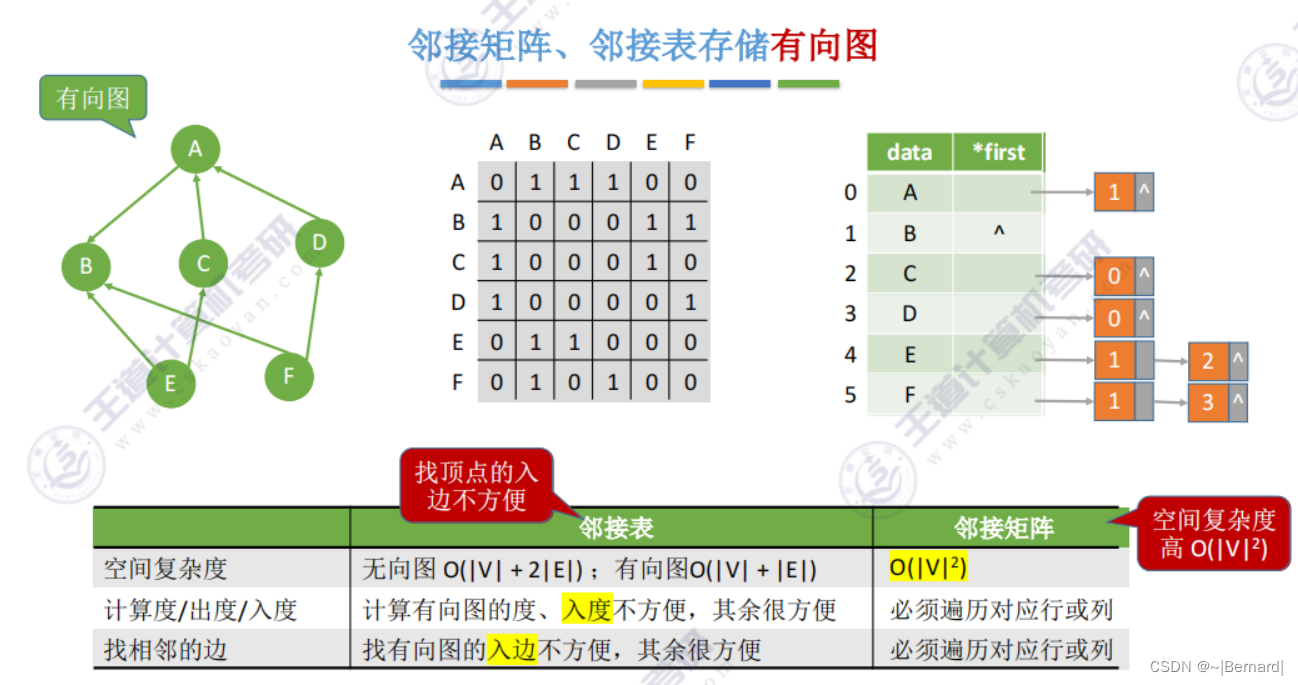
 6.2.1 邻接矩阵法

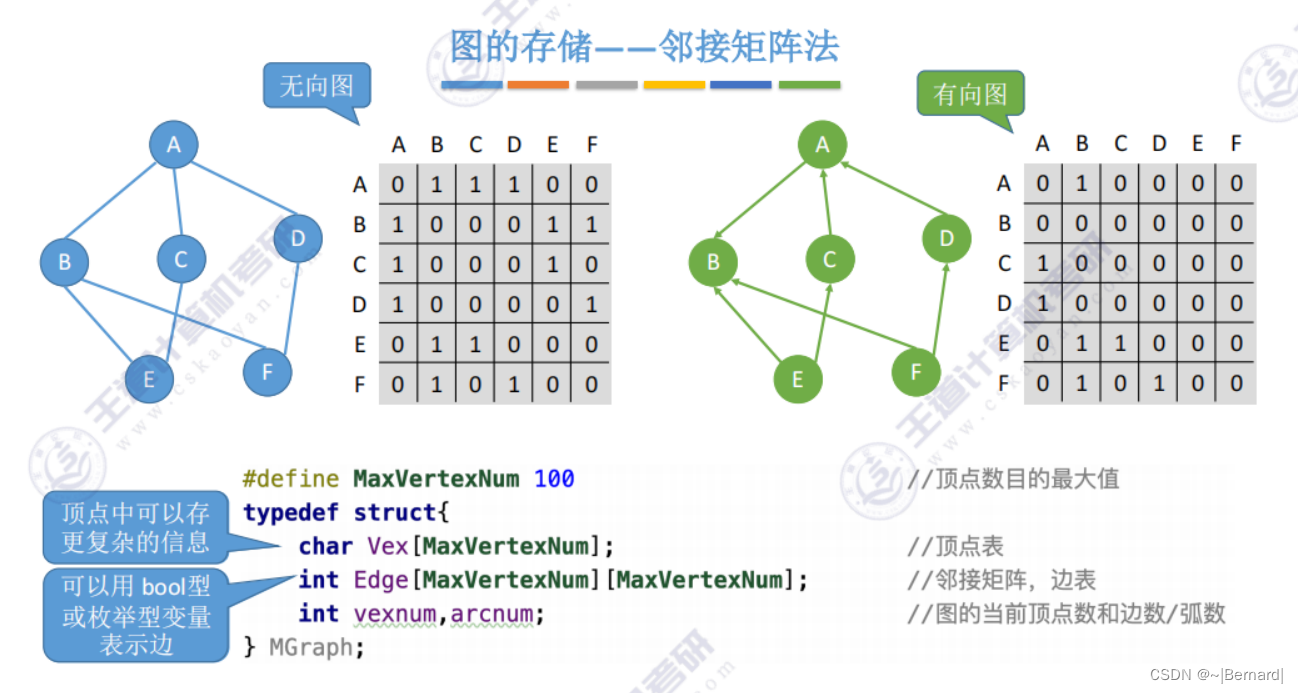
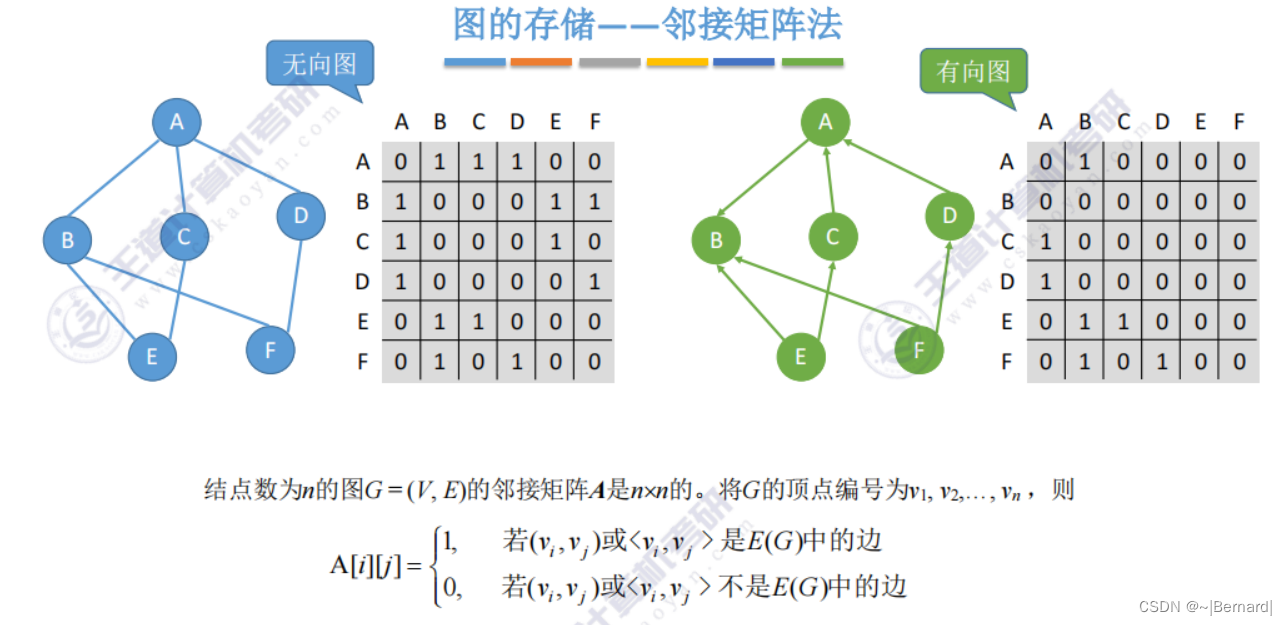
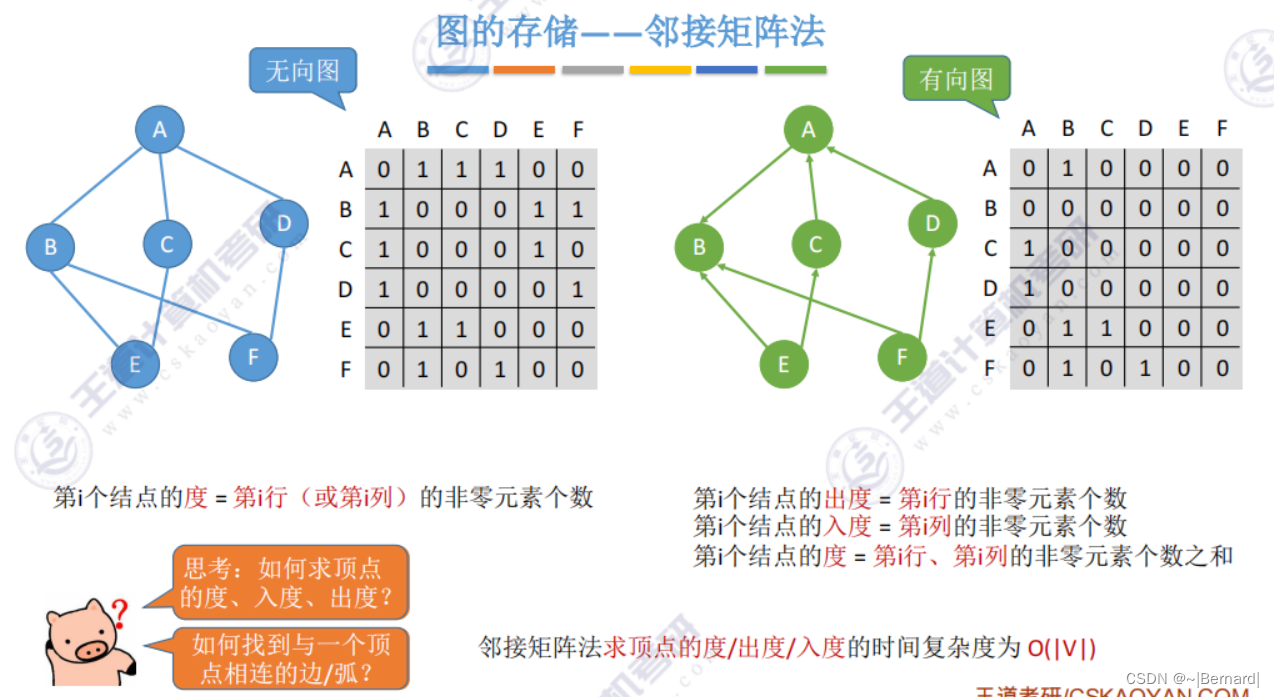
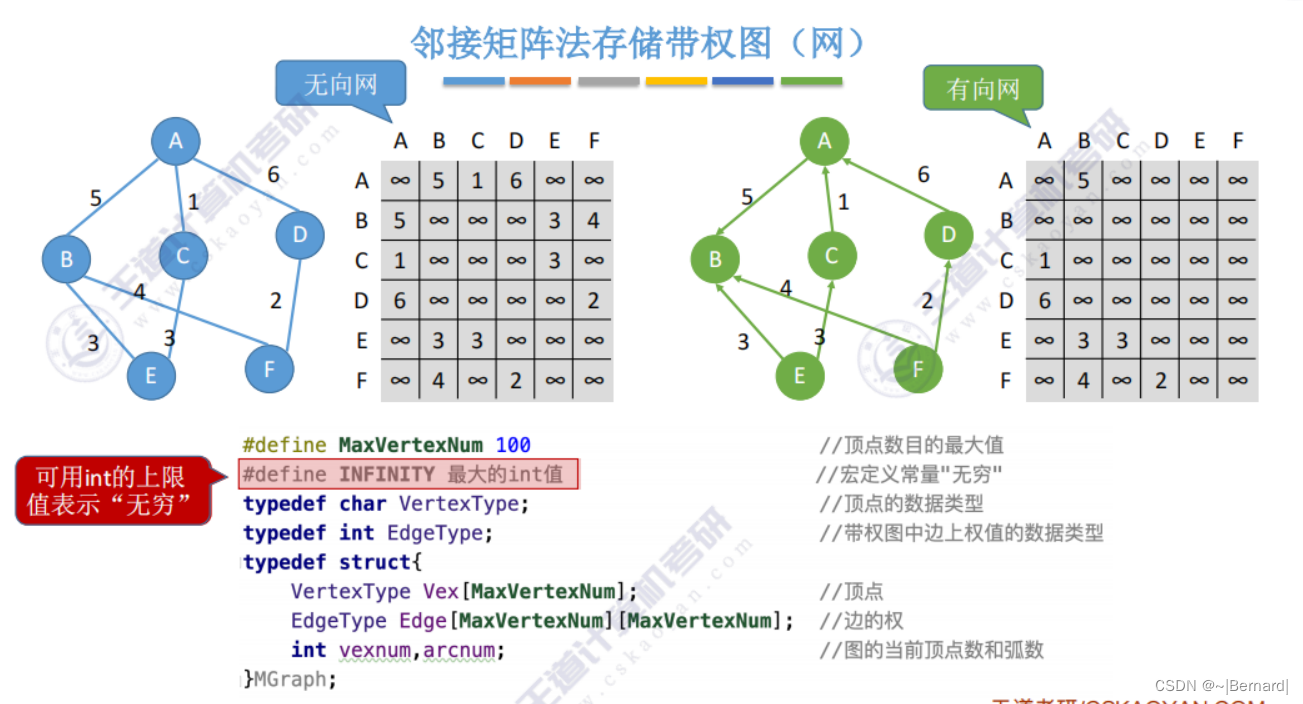
有时也会把0设置为两个顶点之间不存在边 

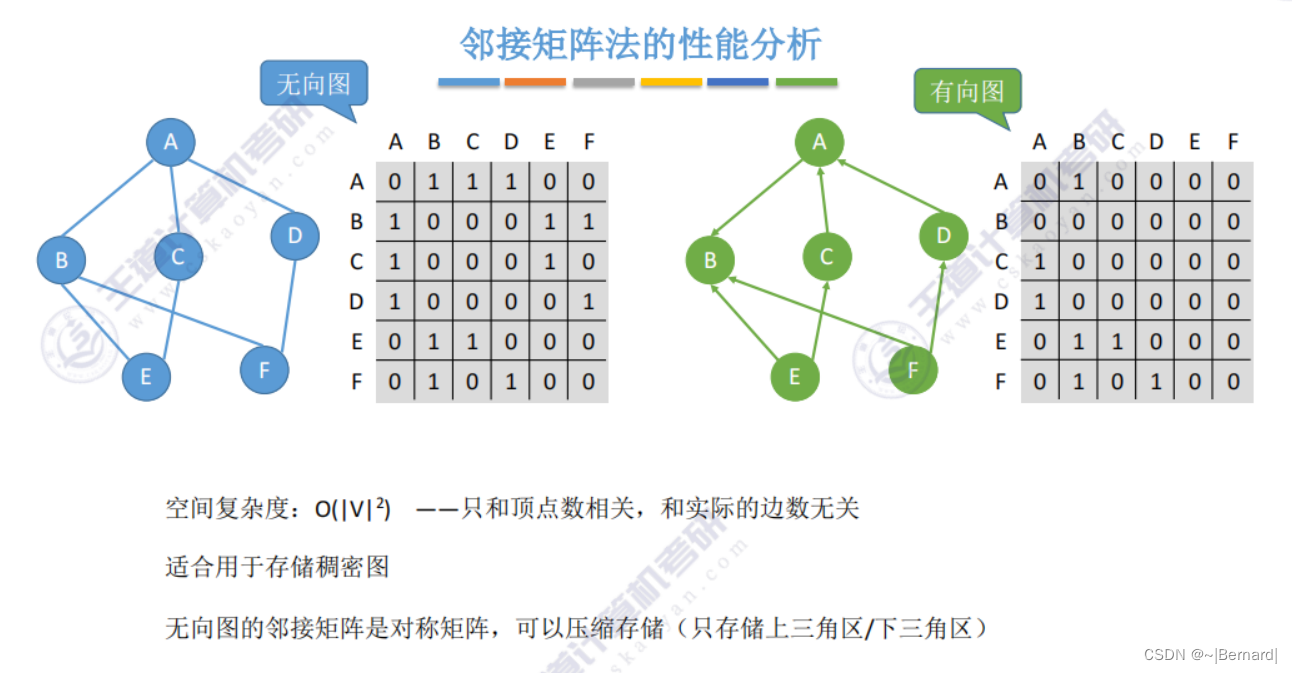
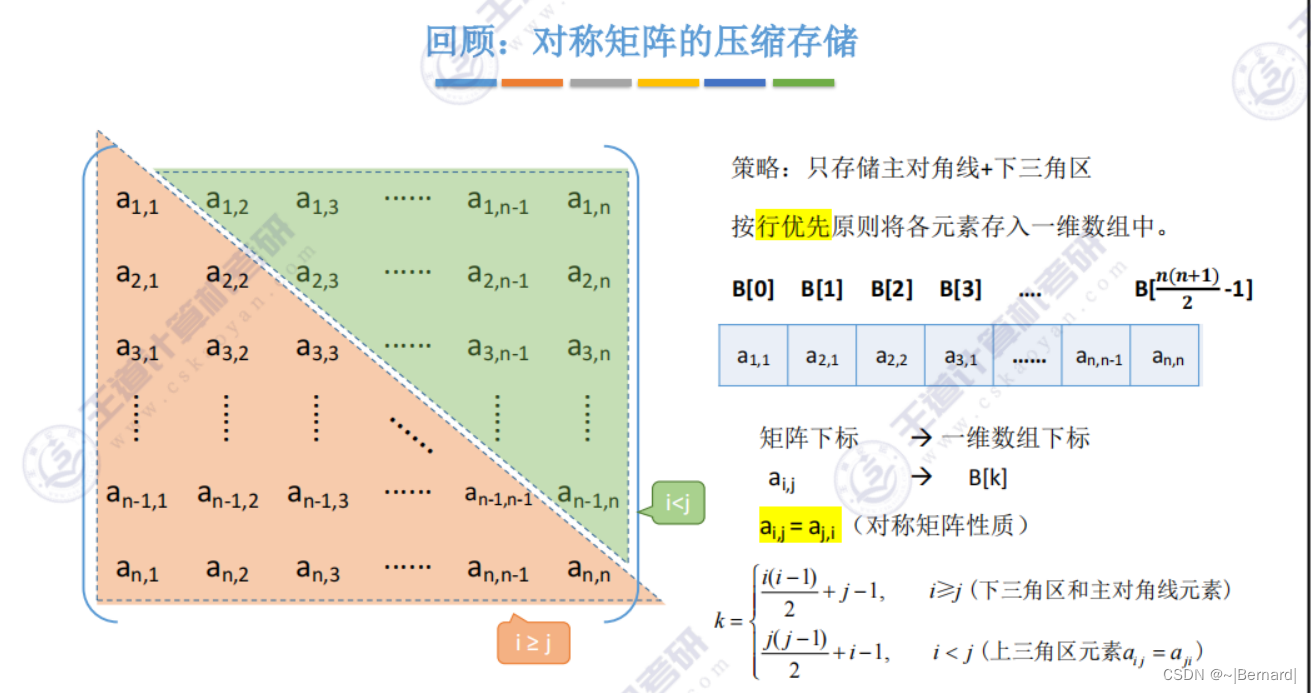
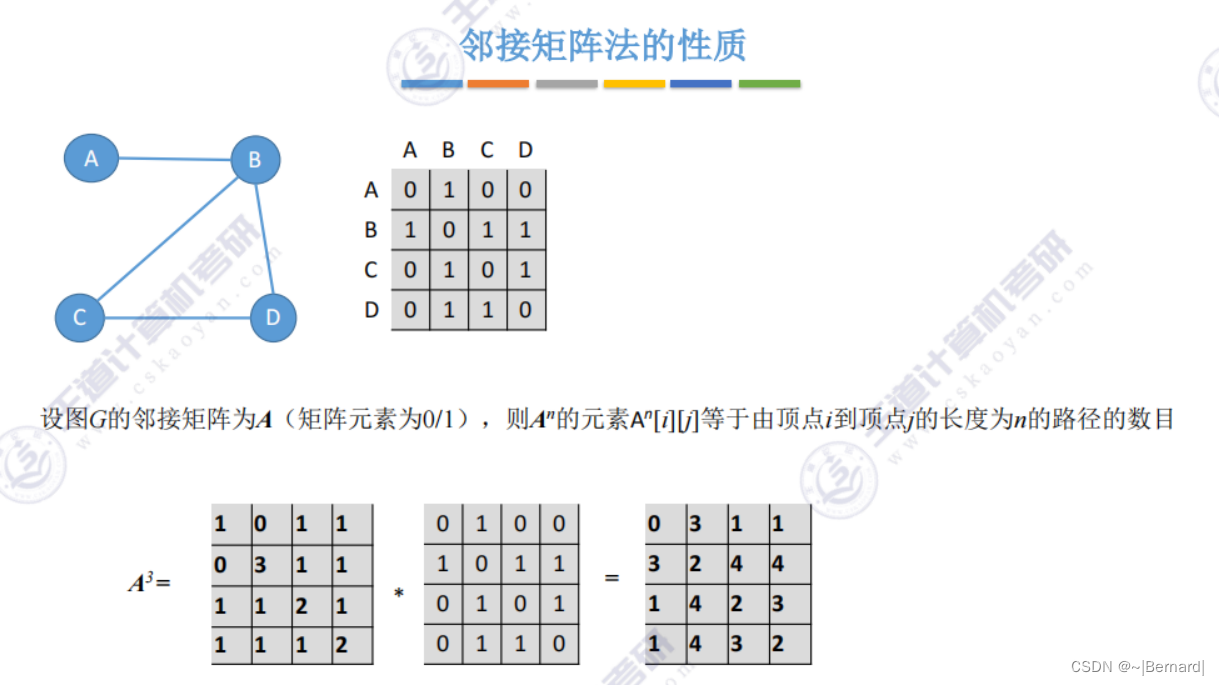
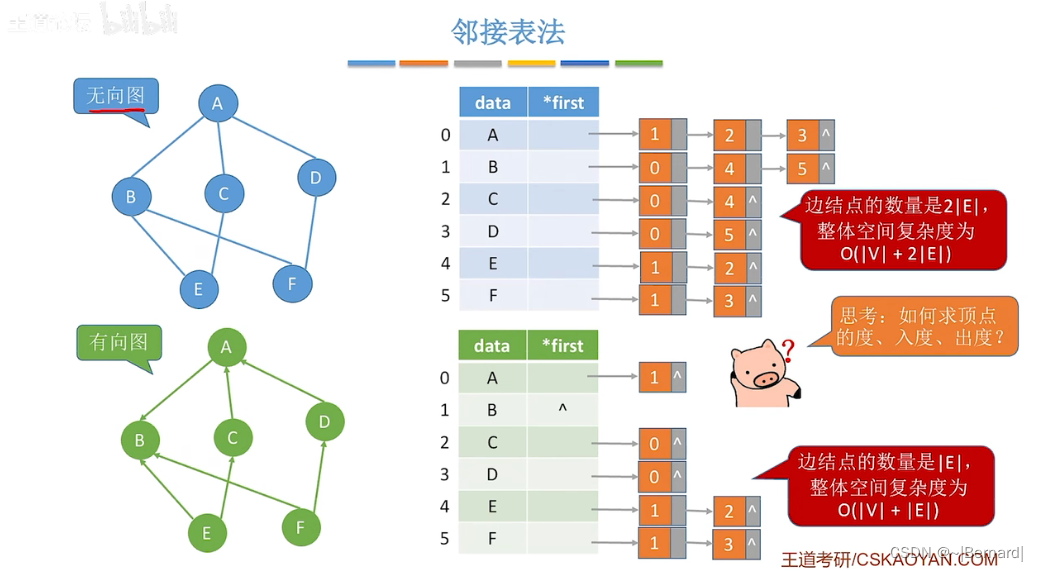
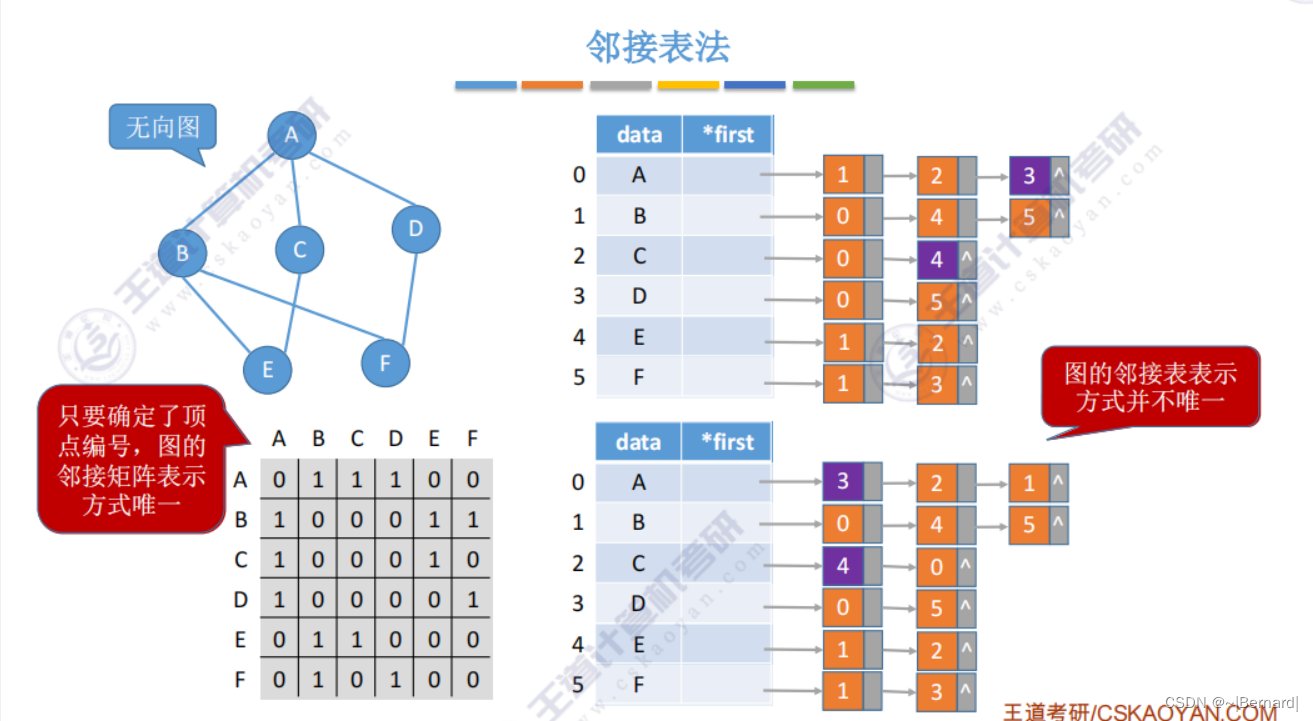
 6.2.2 邻接表法

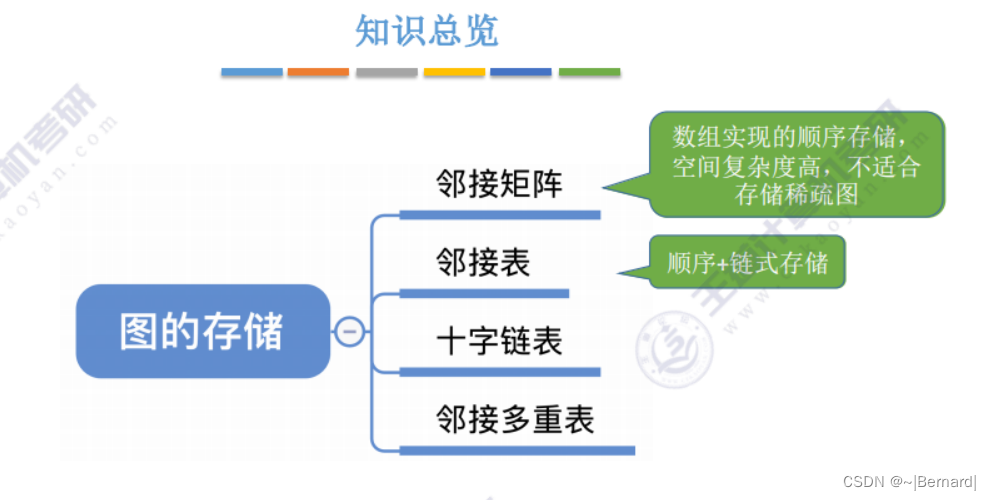
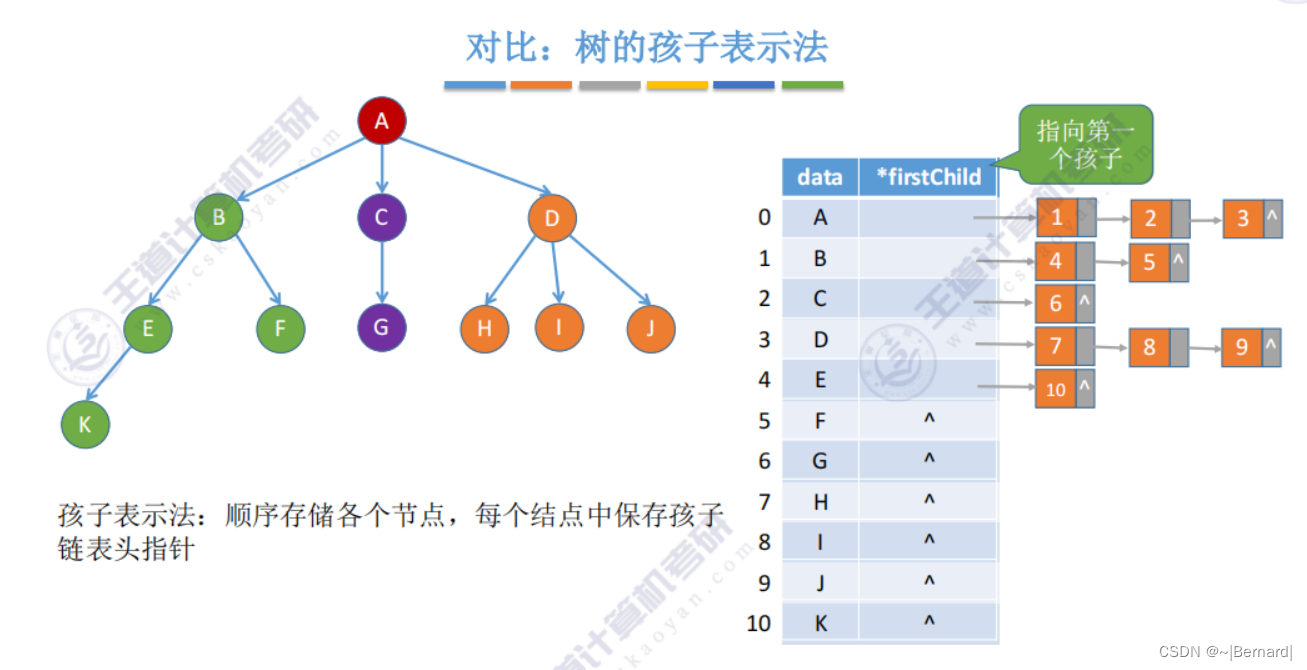
 邻接表法类似于树中的孩子表示法

 

 

6.2.3 十字链表，邻接多重表

 

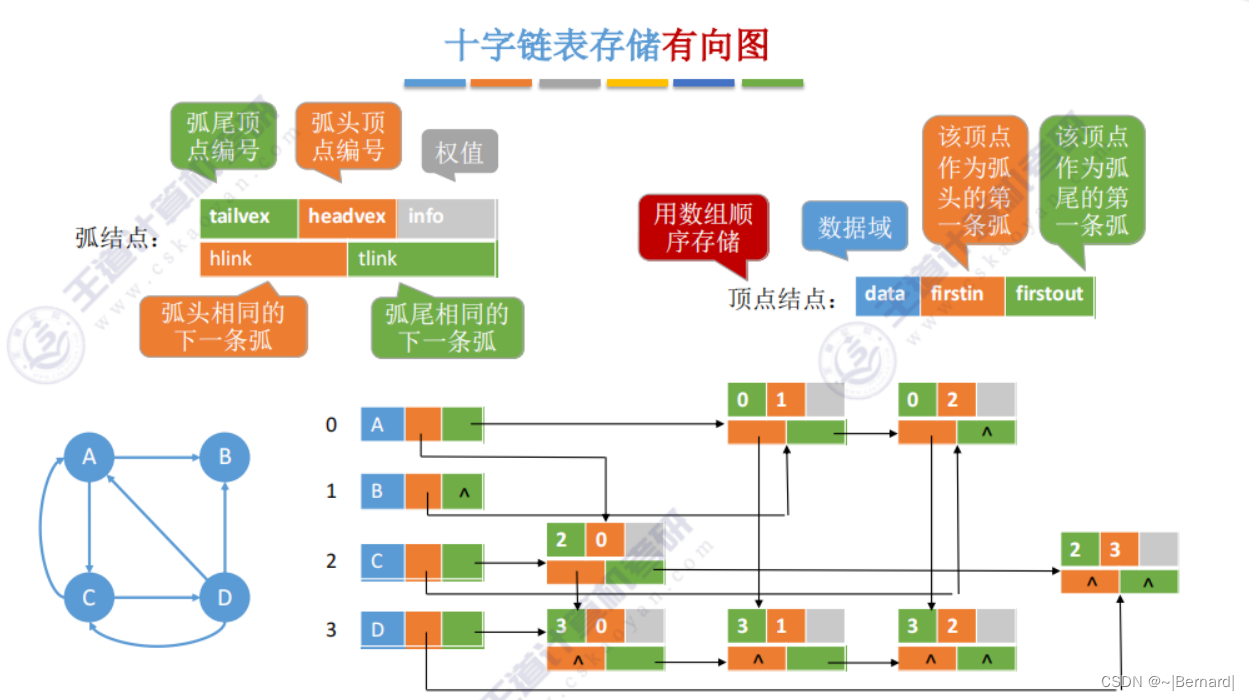
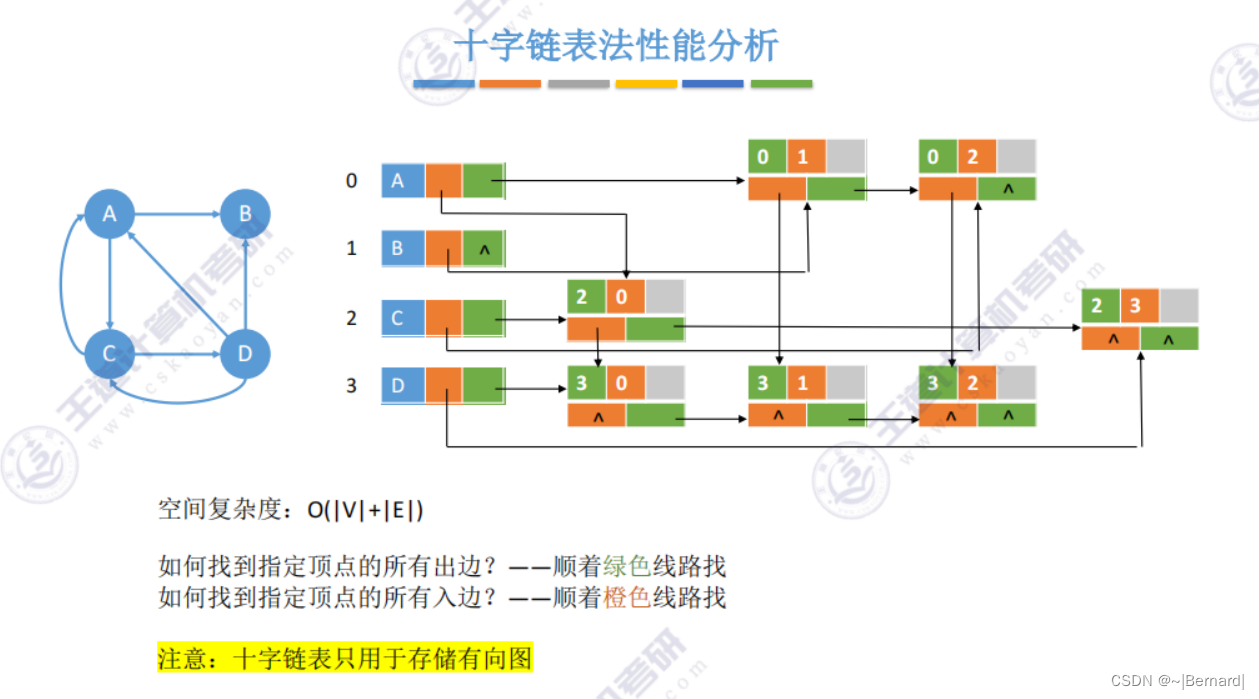
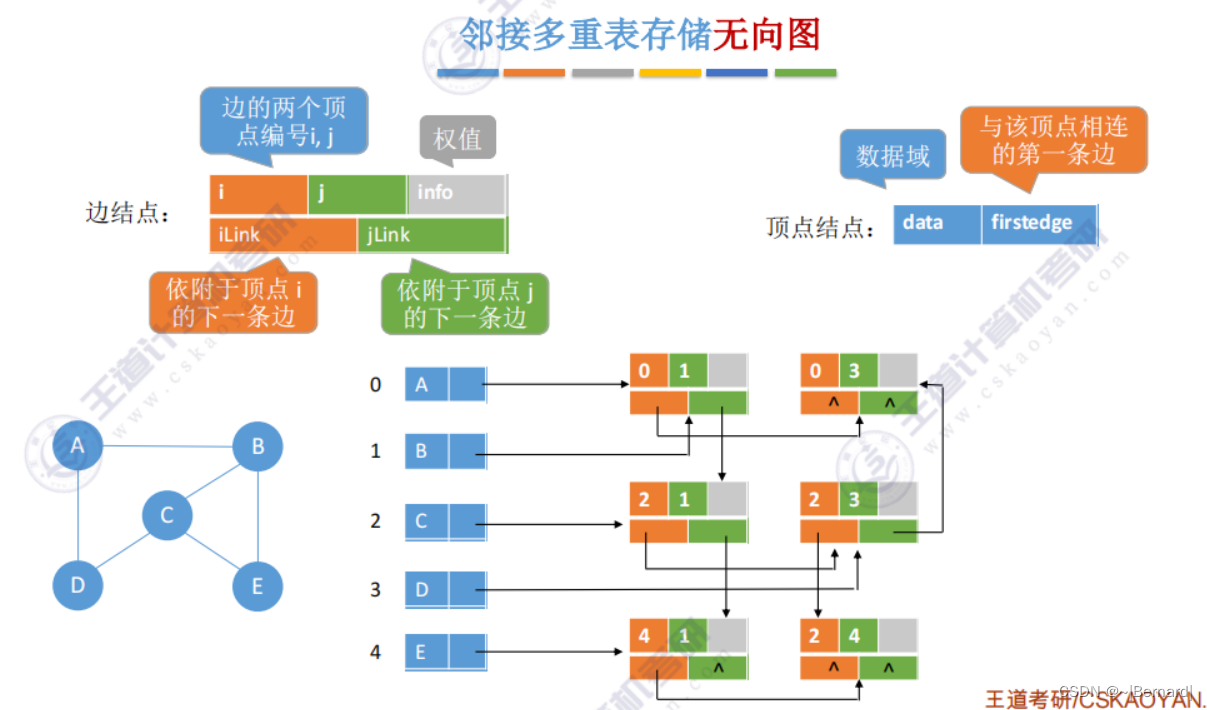
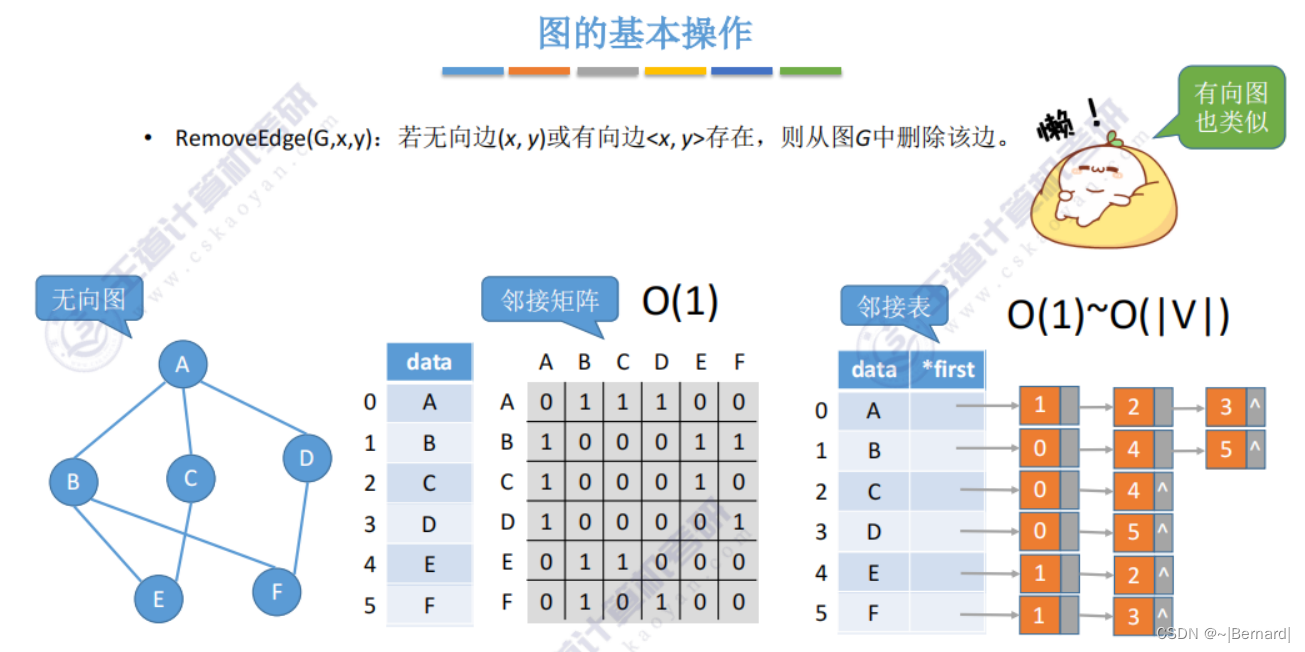
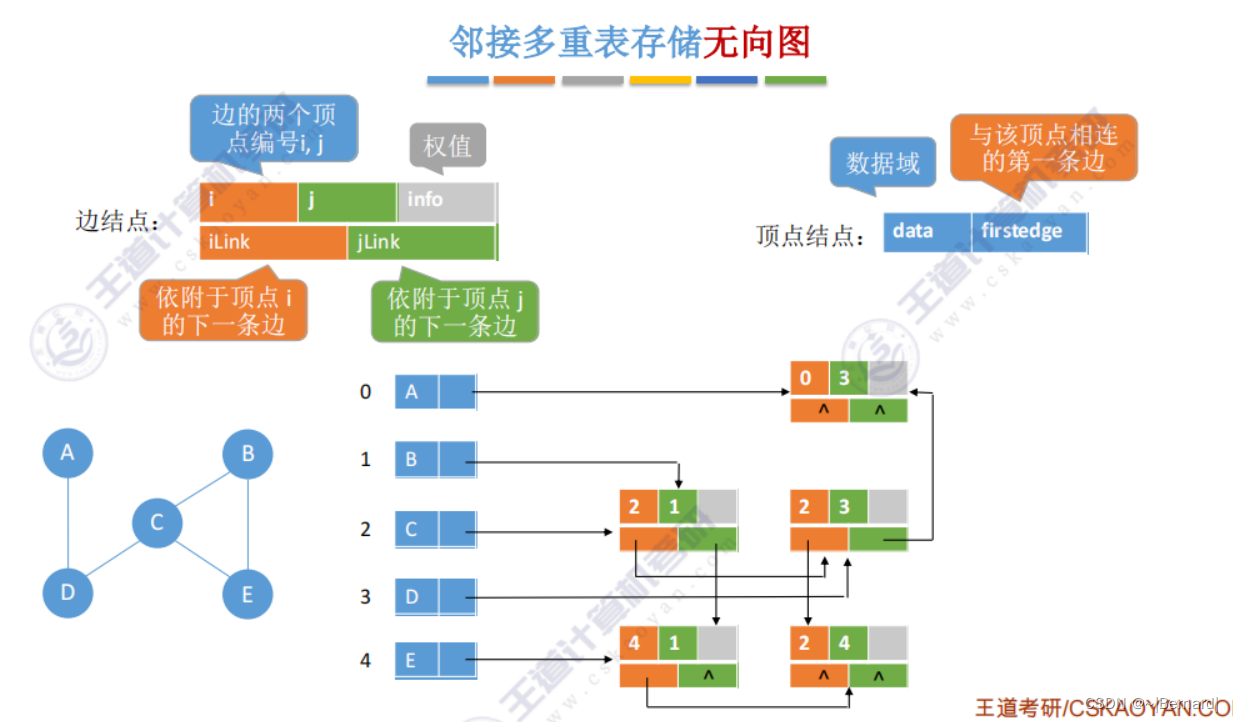 删除边(A，B)

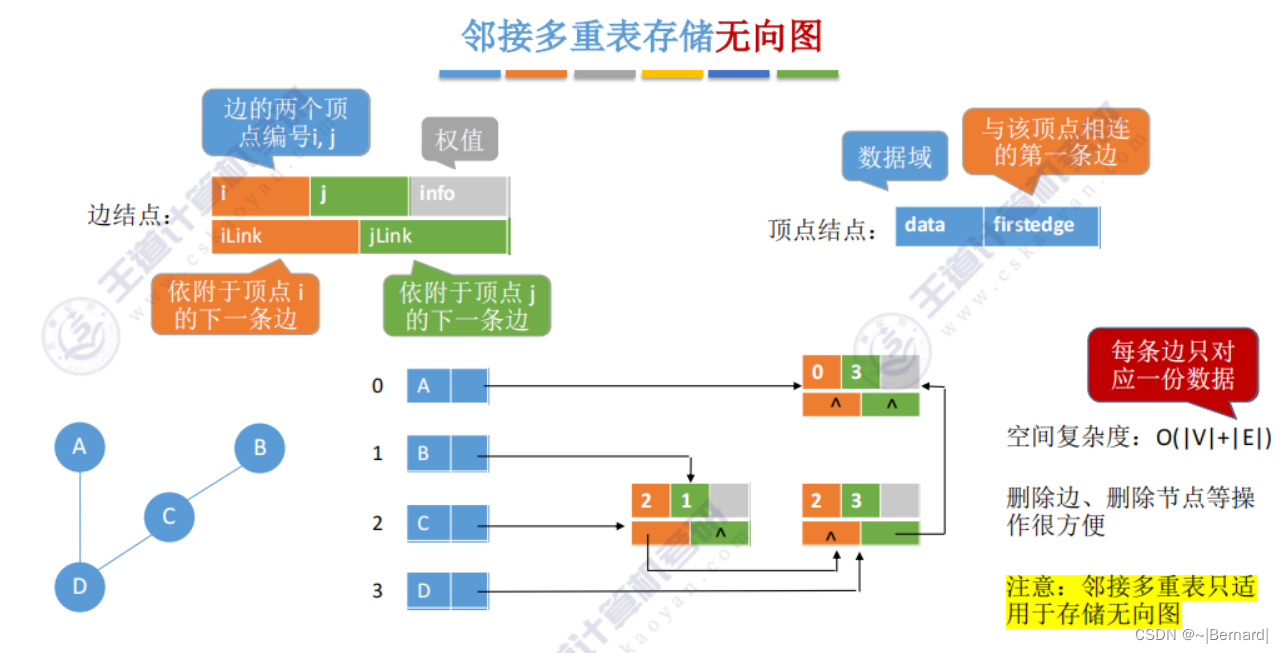
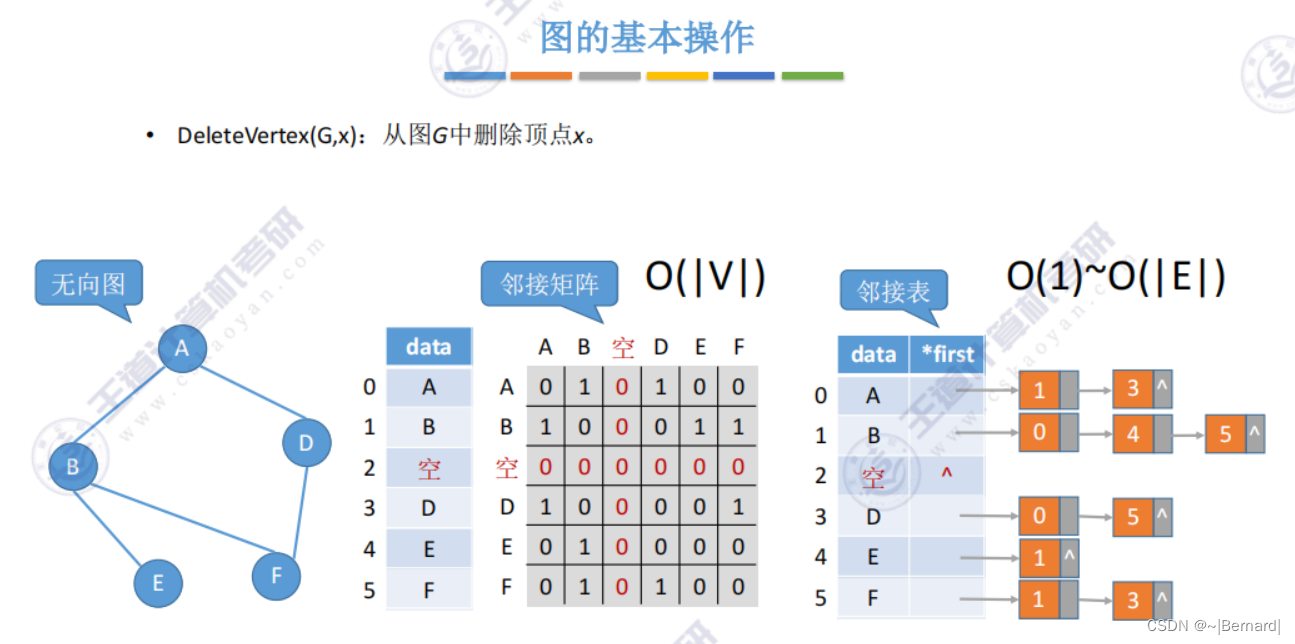
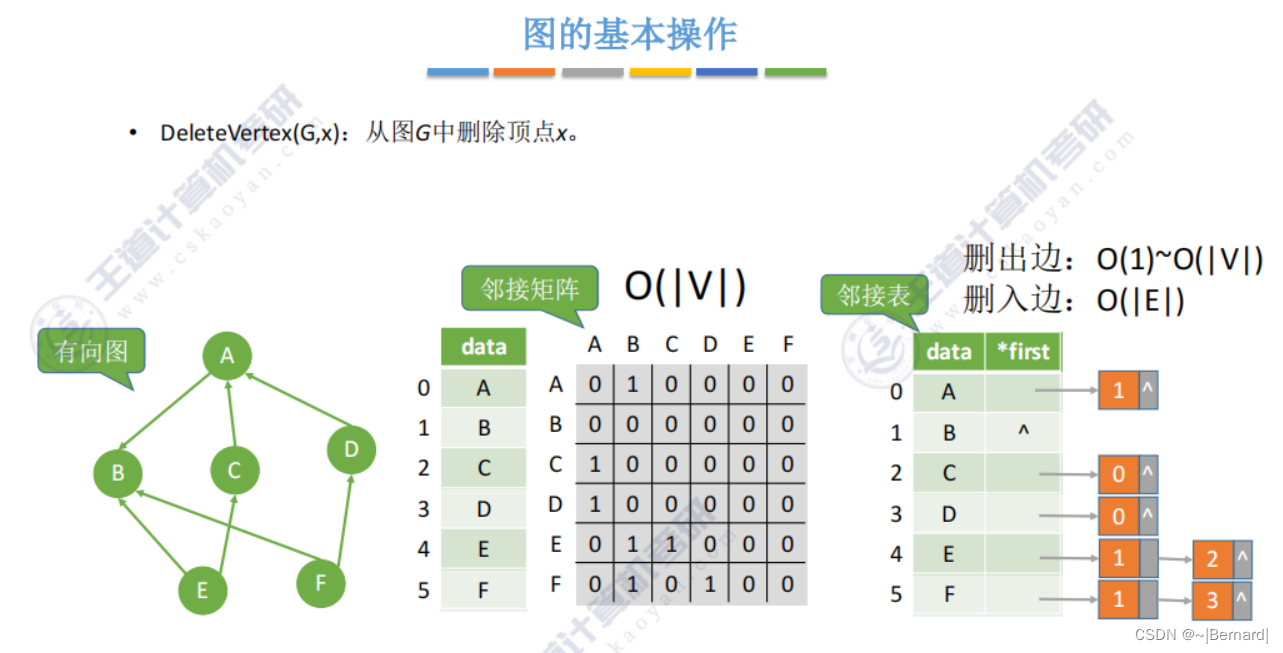
 删除点E 

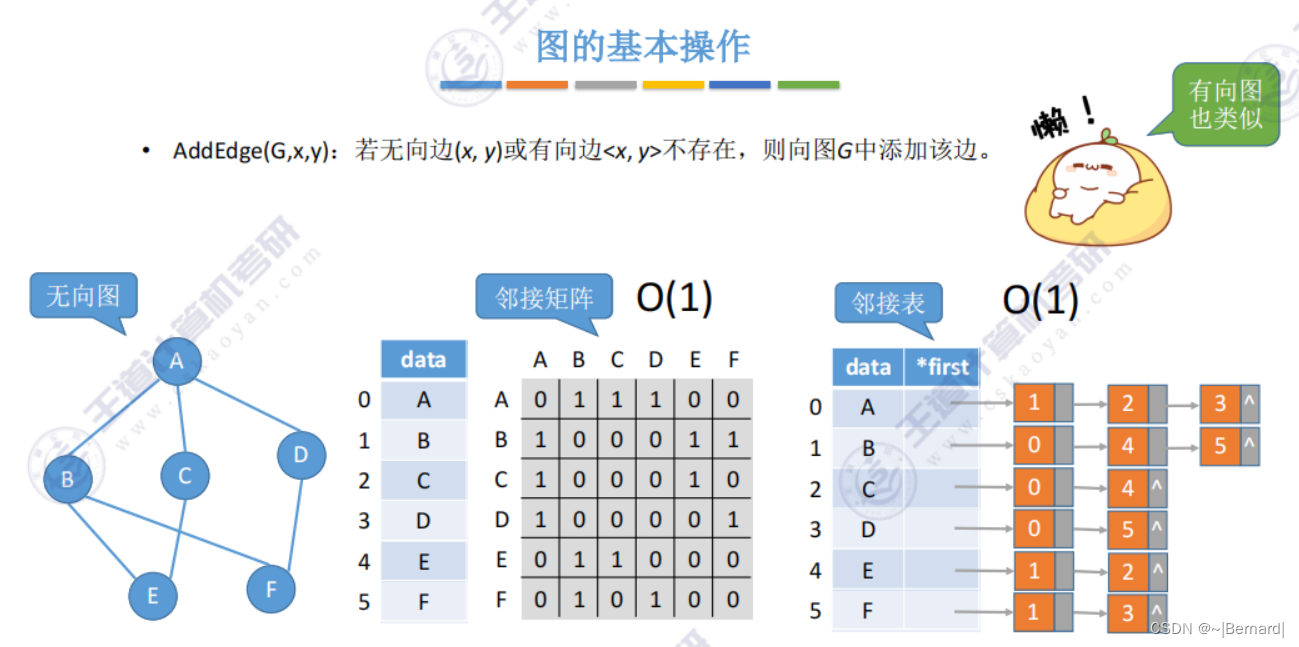
 6.2.4 图的基本操作

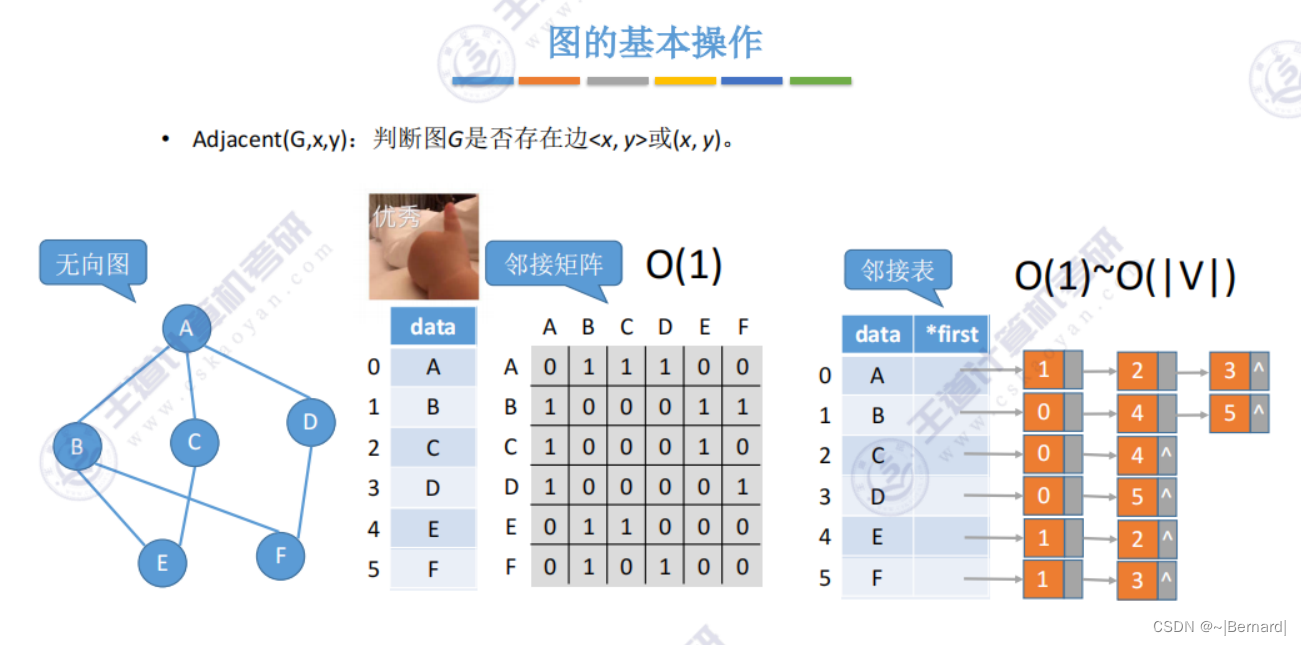
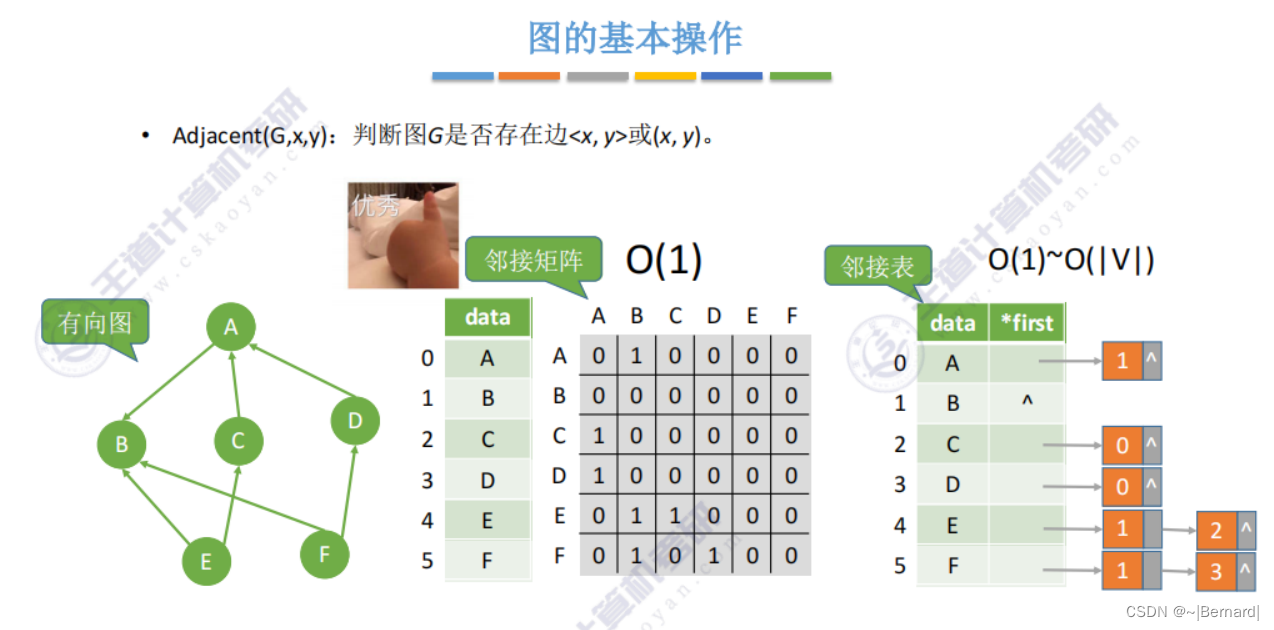
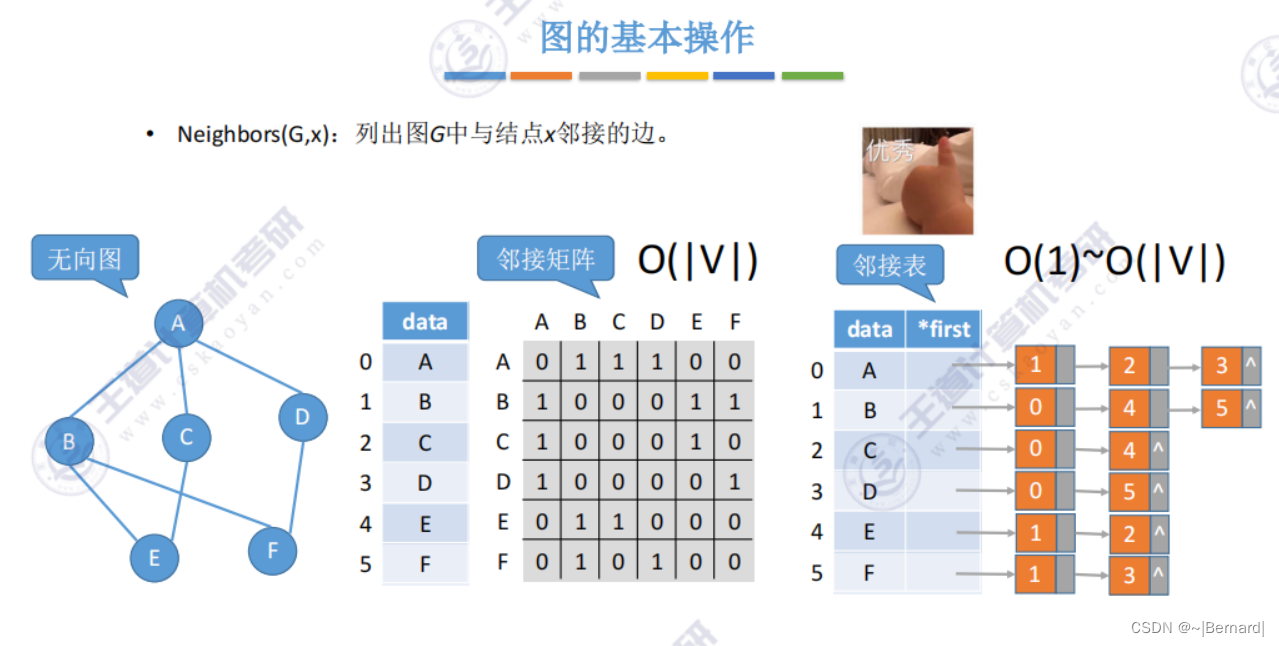
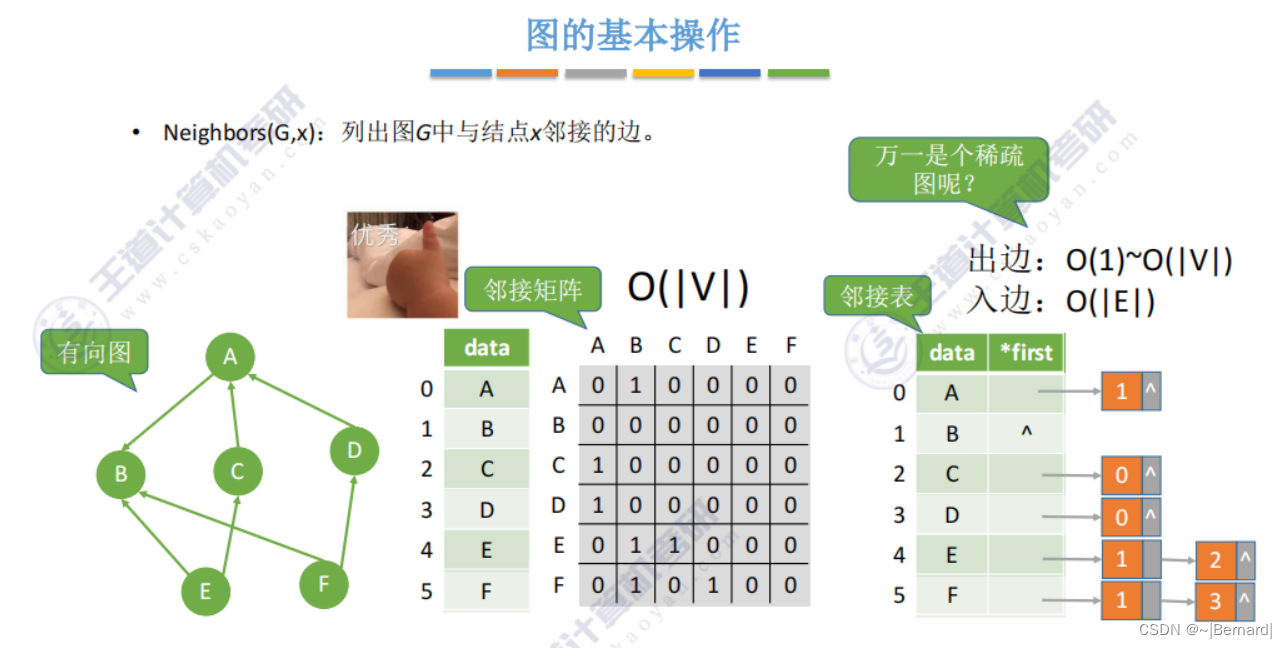
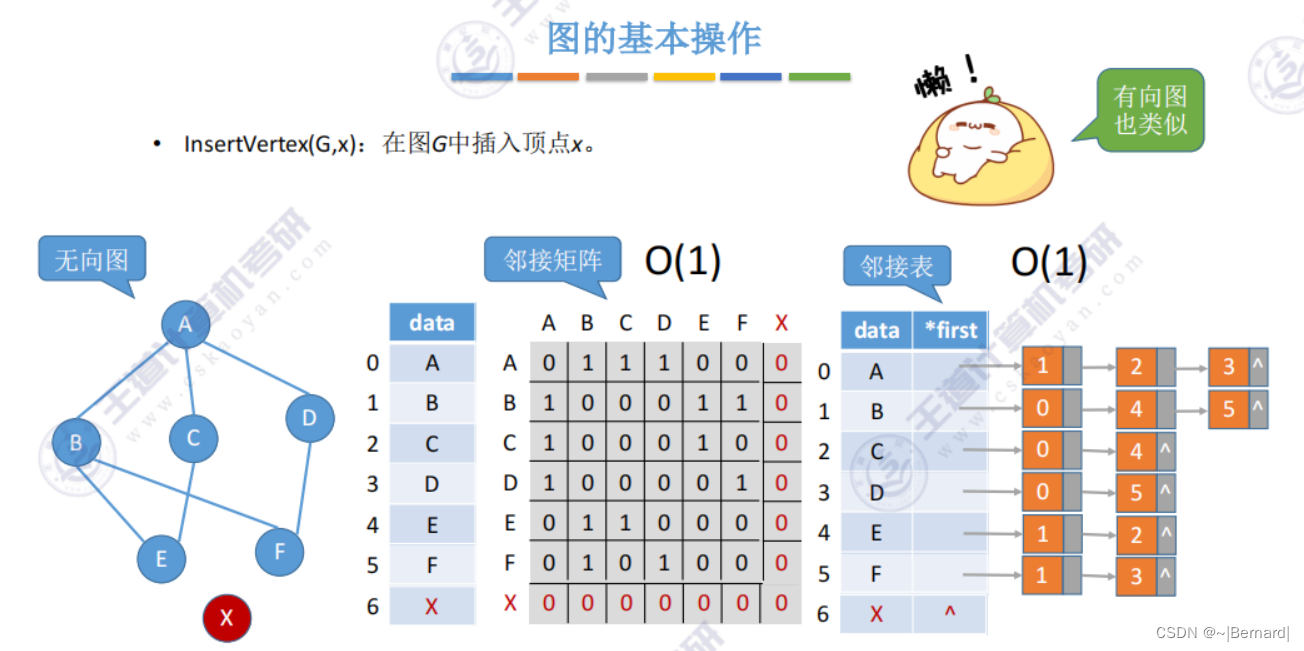
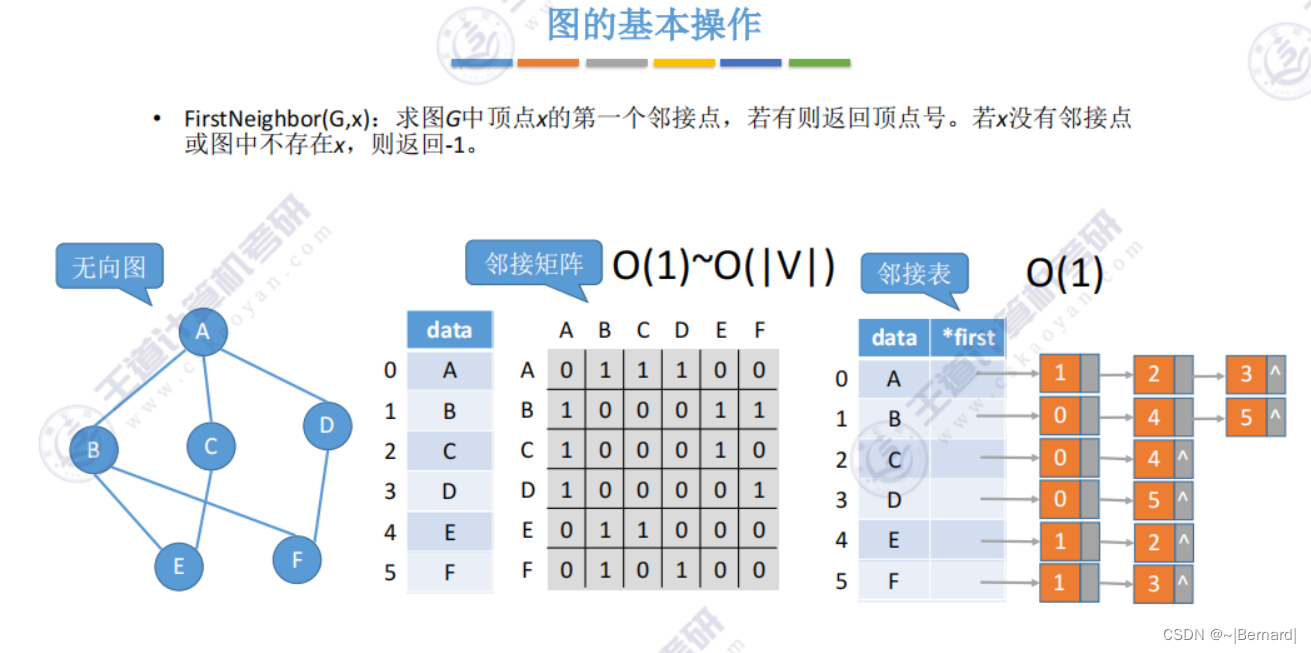
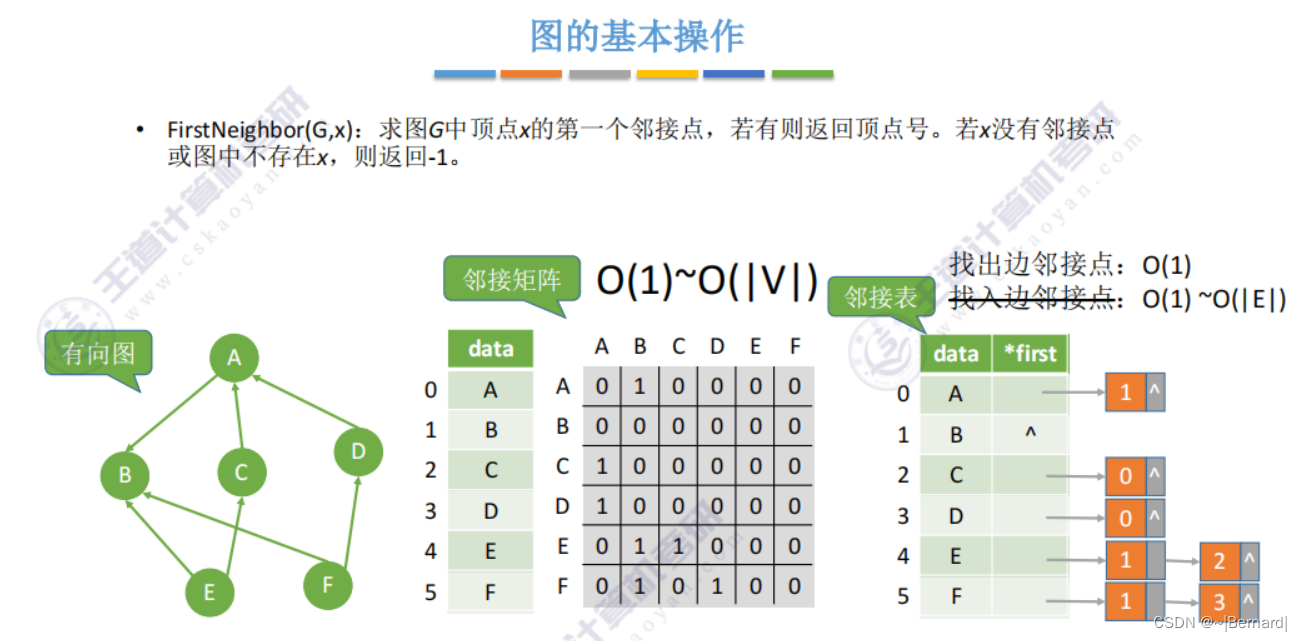
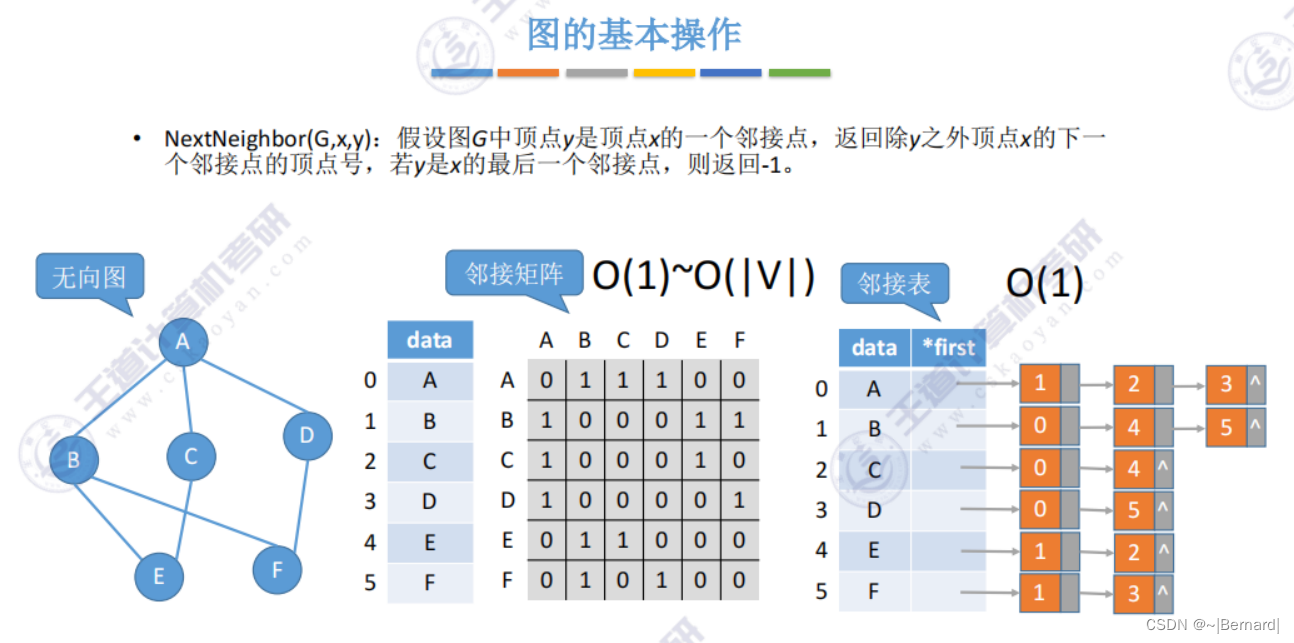
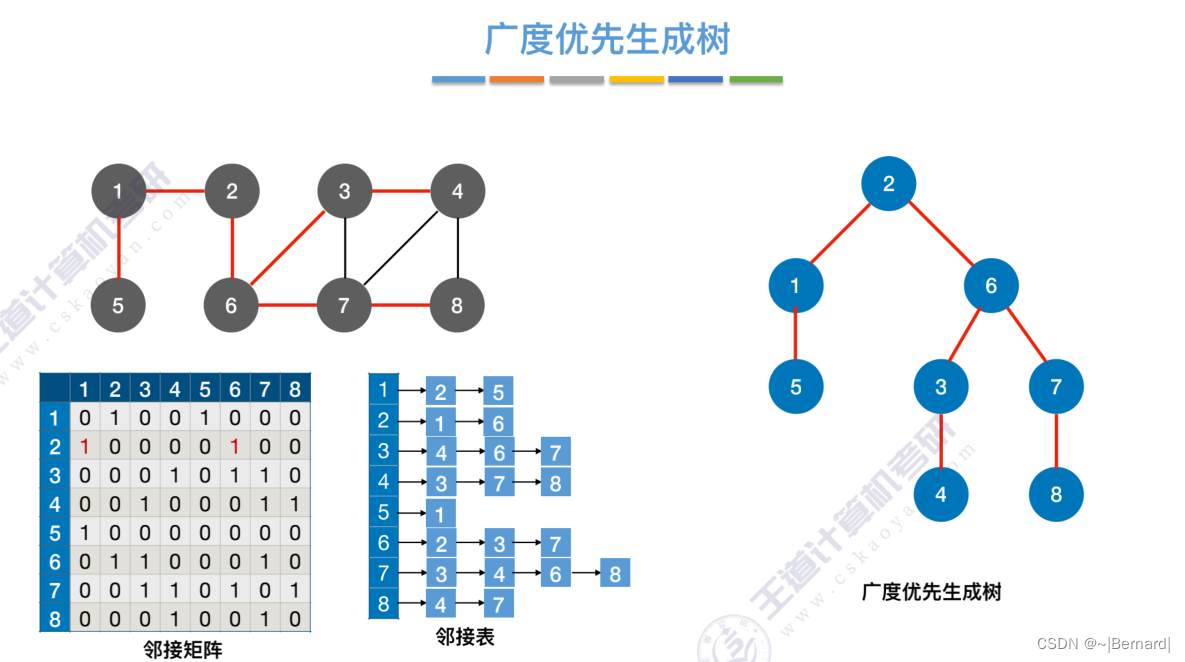
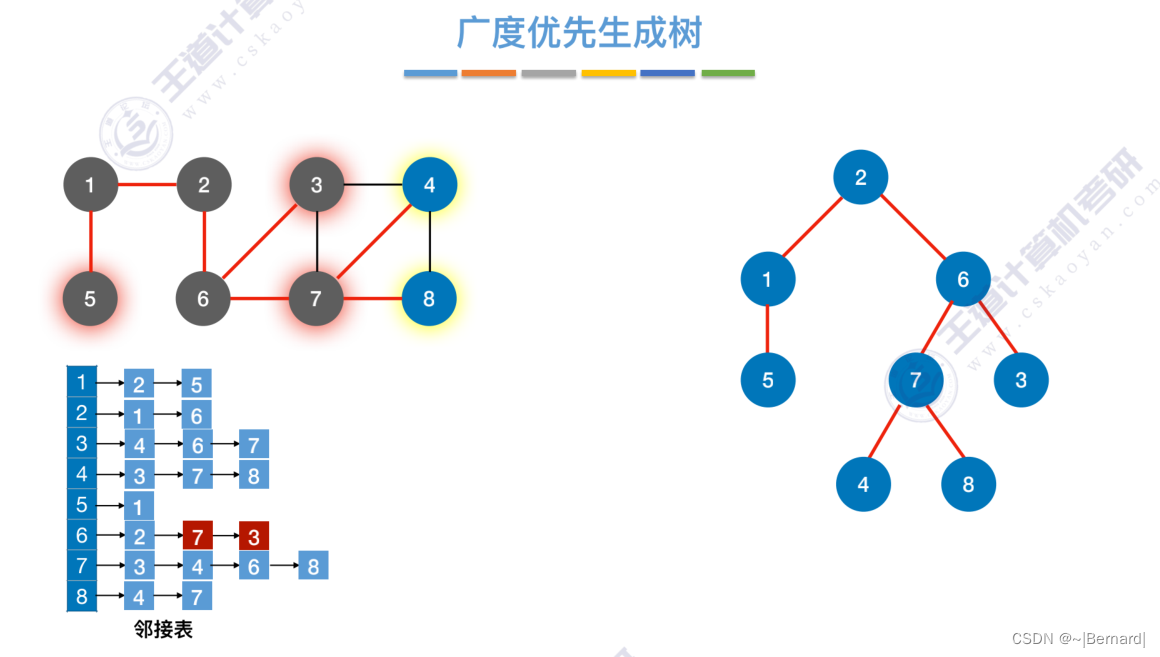
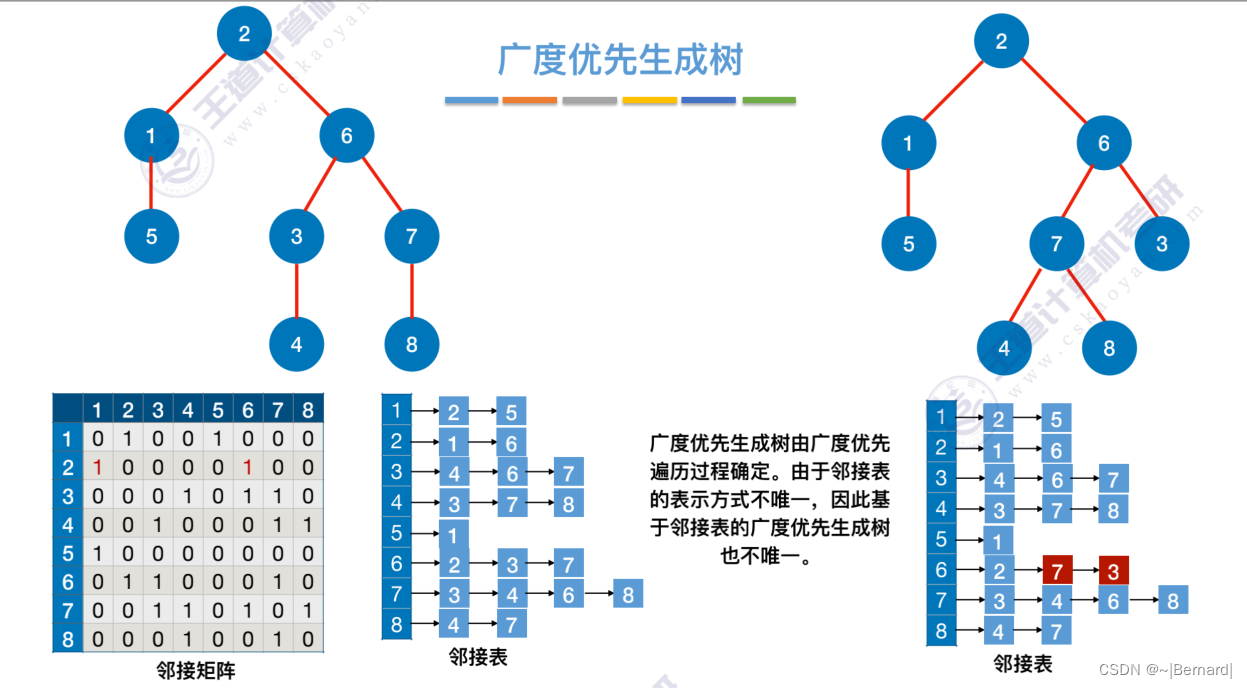
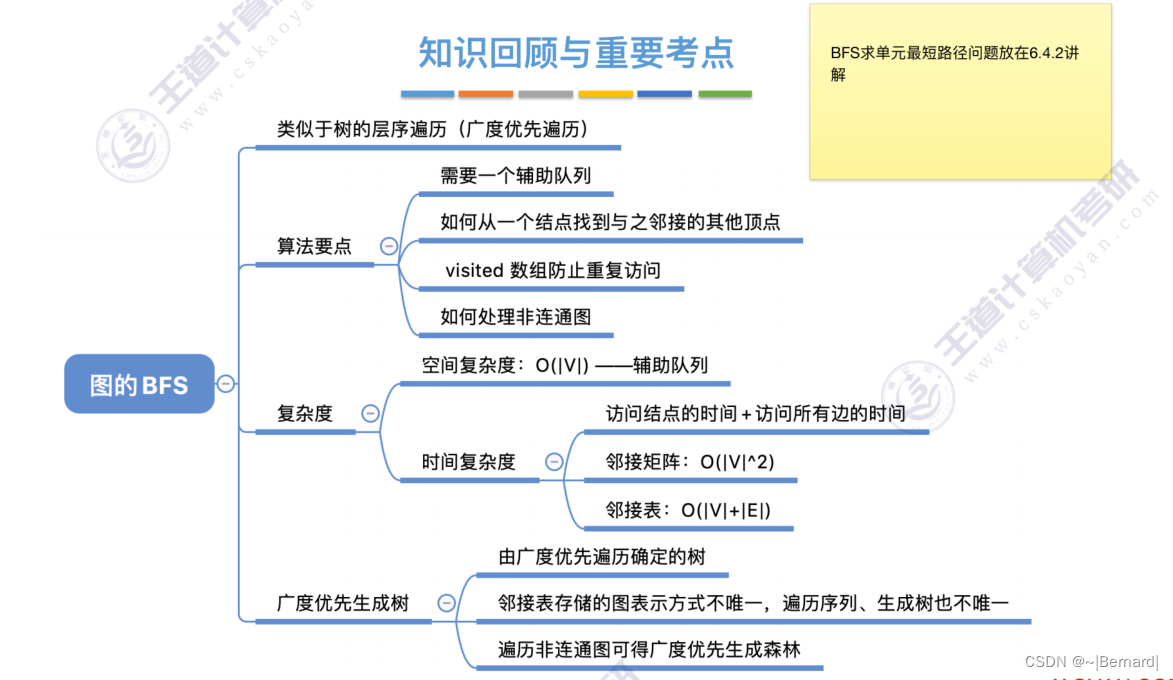
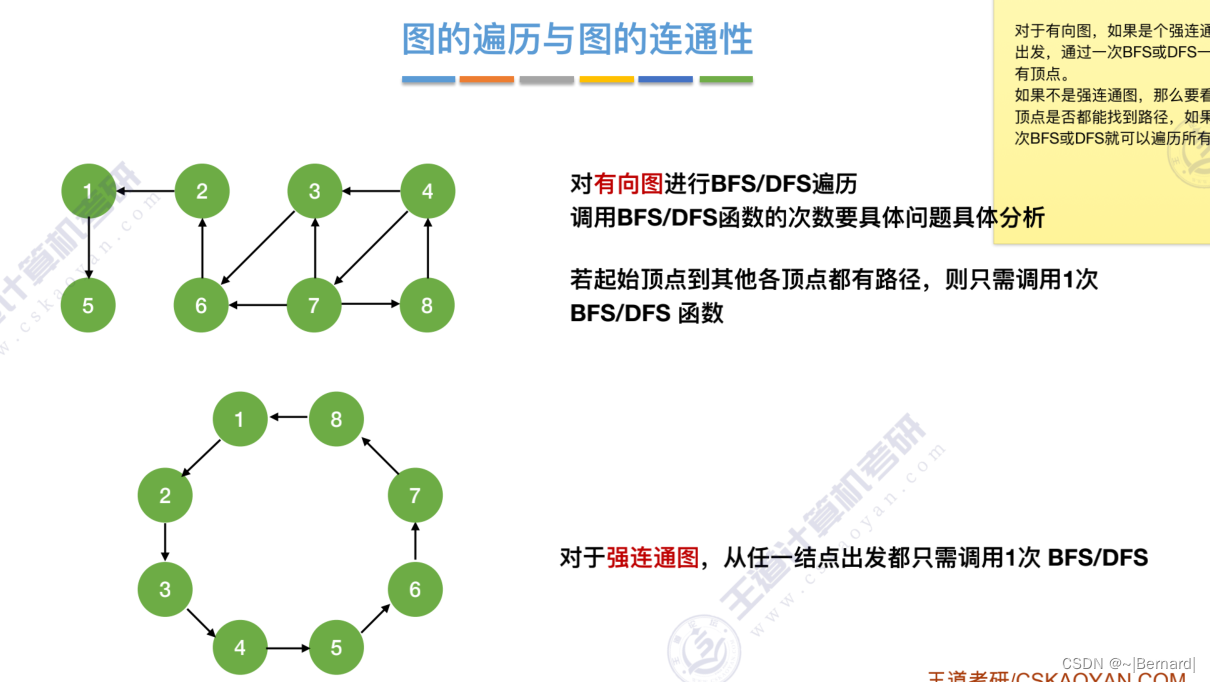
 6.3.1 图的广度优先遍历

 

 

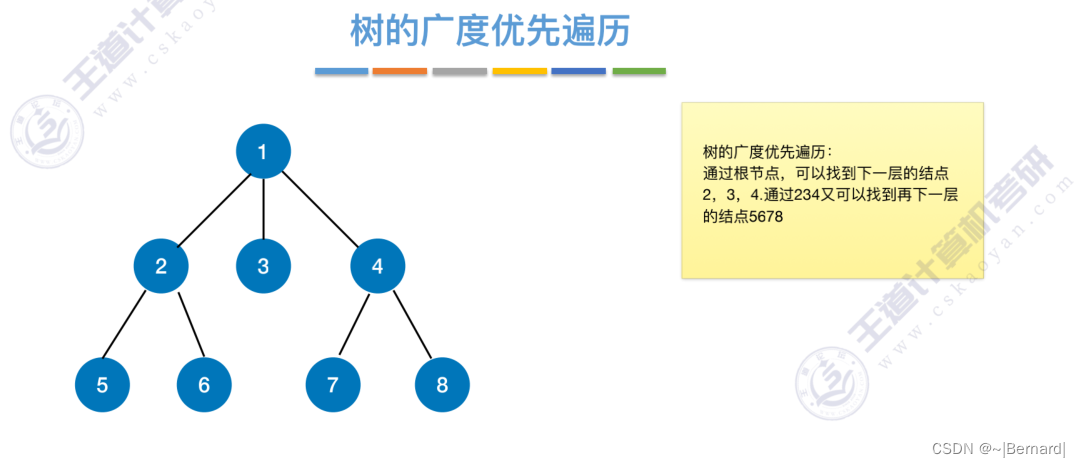
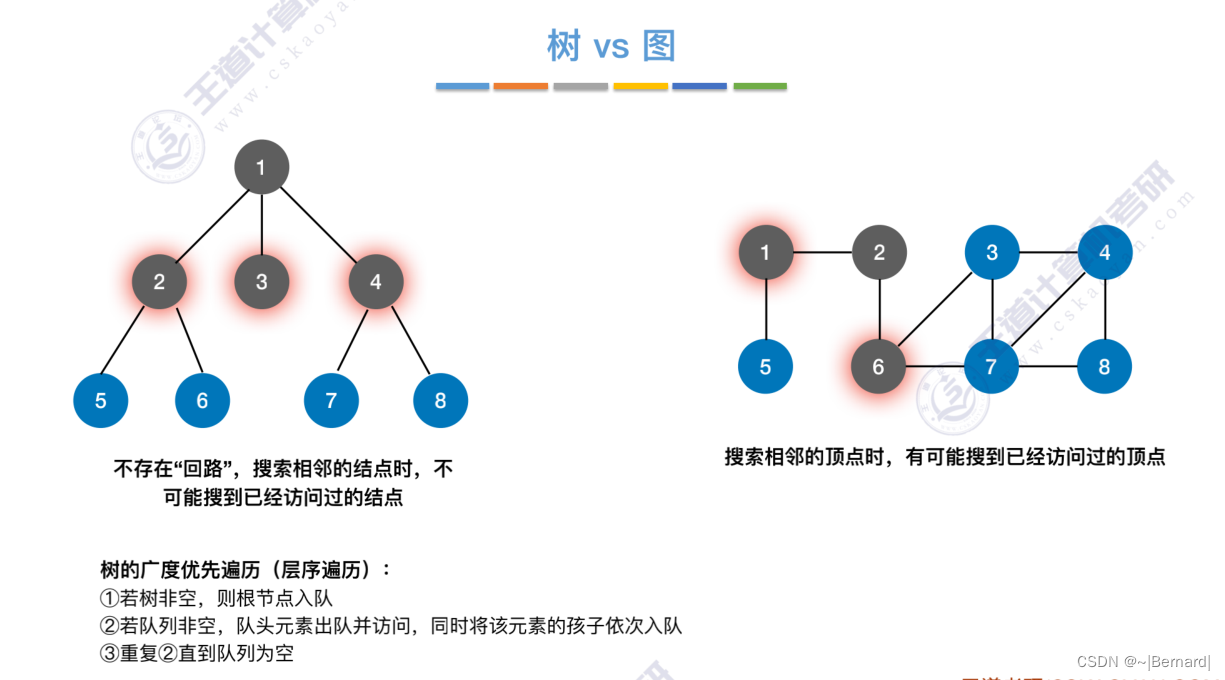
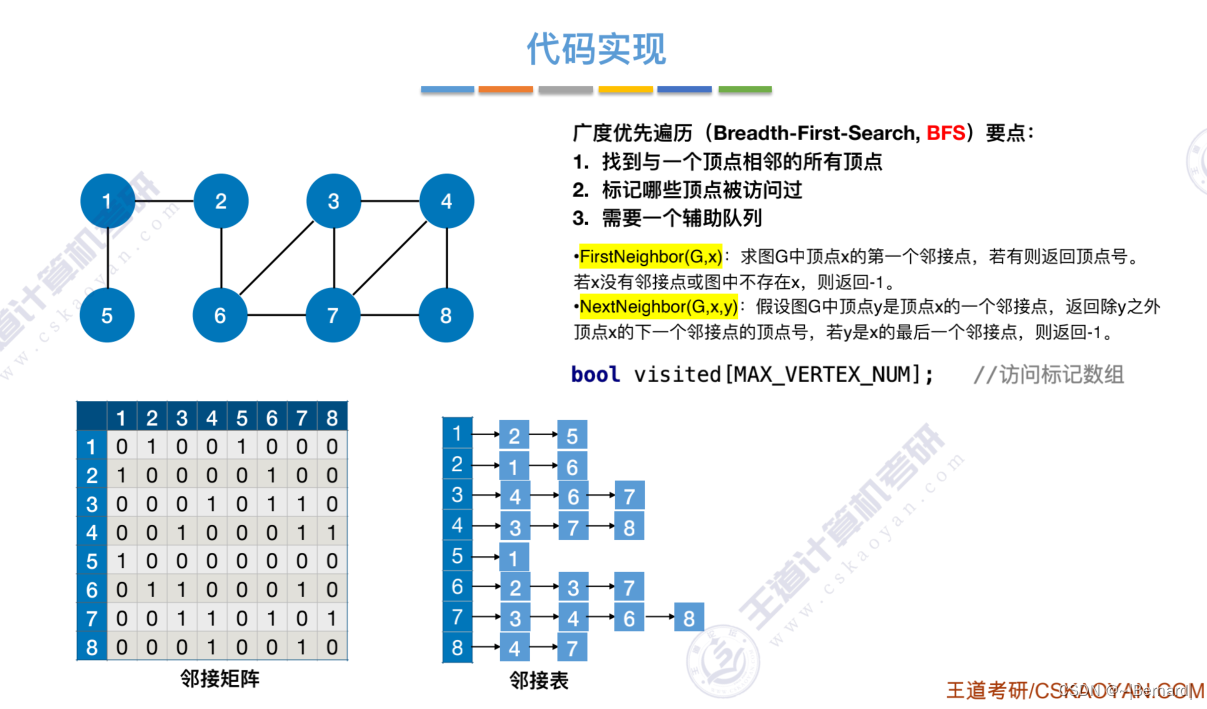
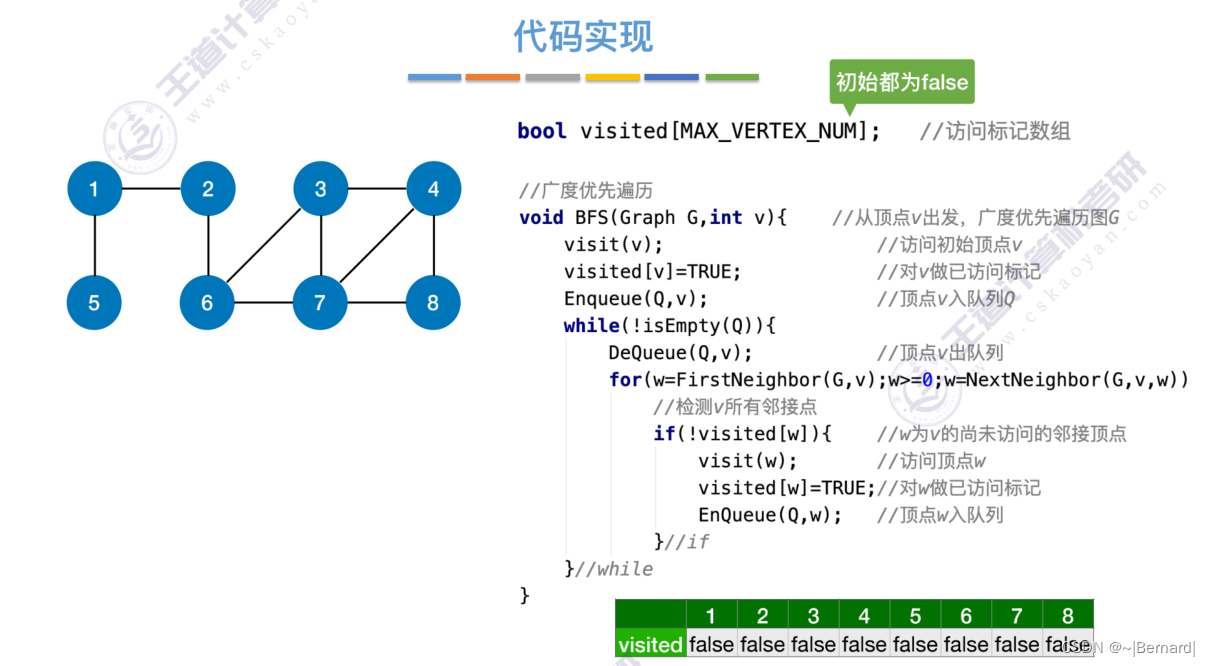
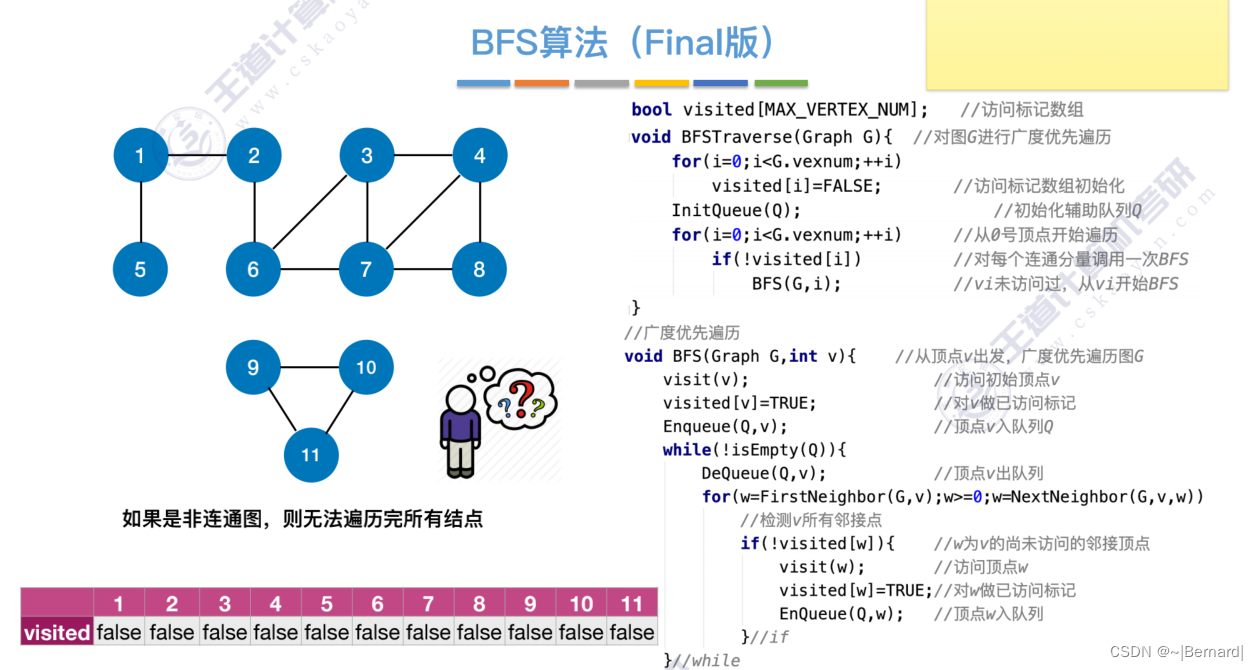
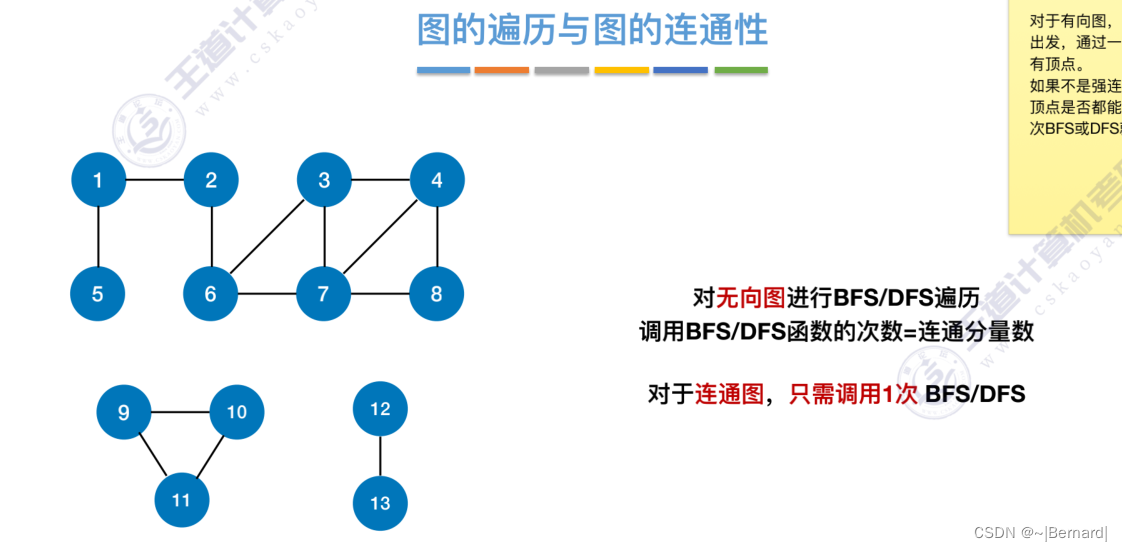
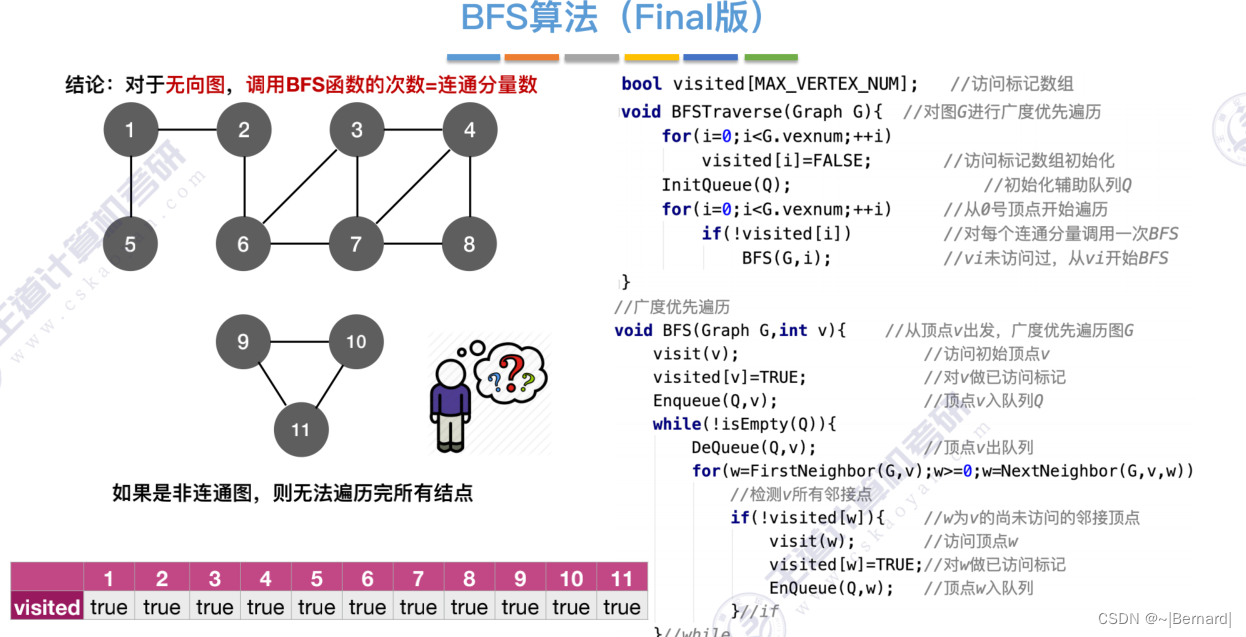 对于无向图来说，调用BFS的次数=连通分量数(极大连通子图)

 

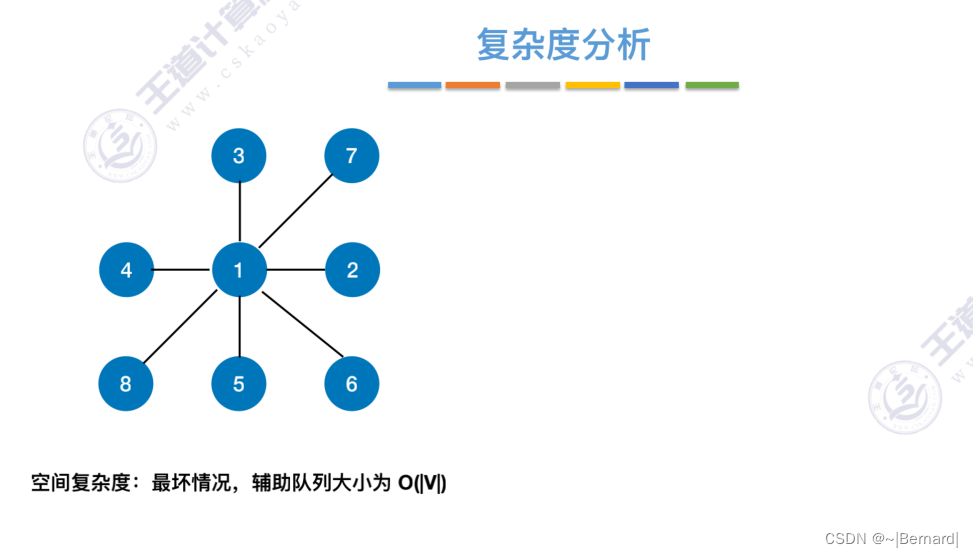
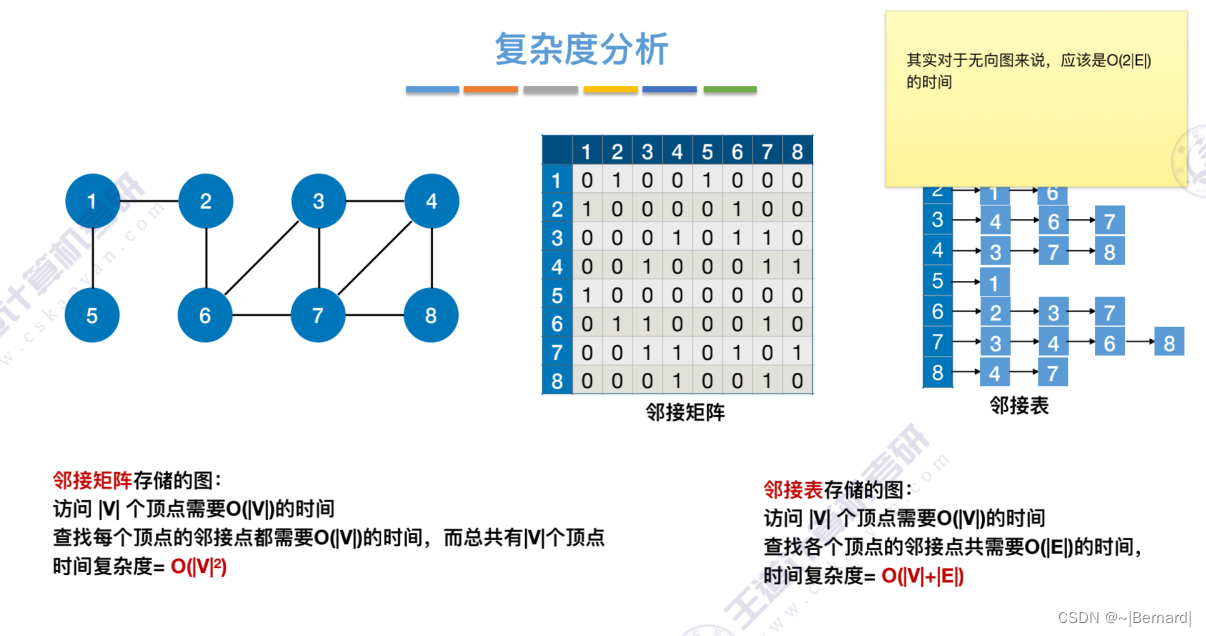
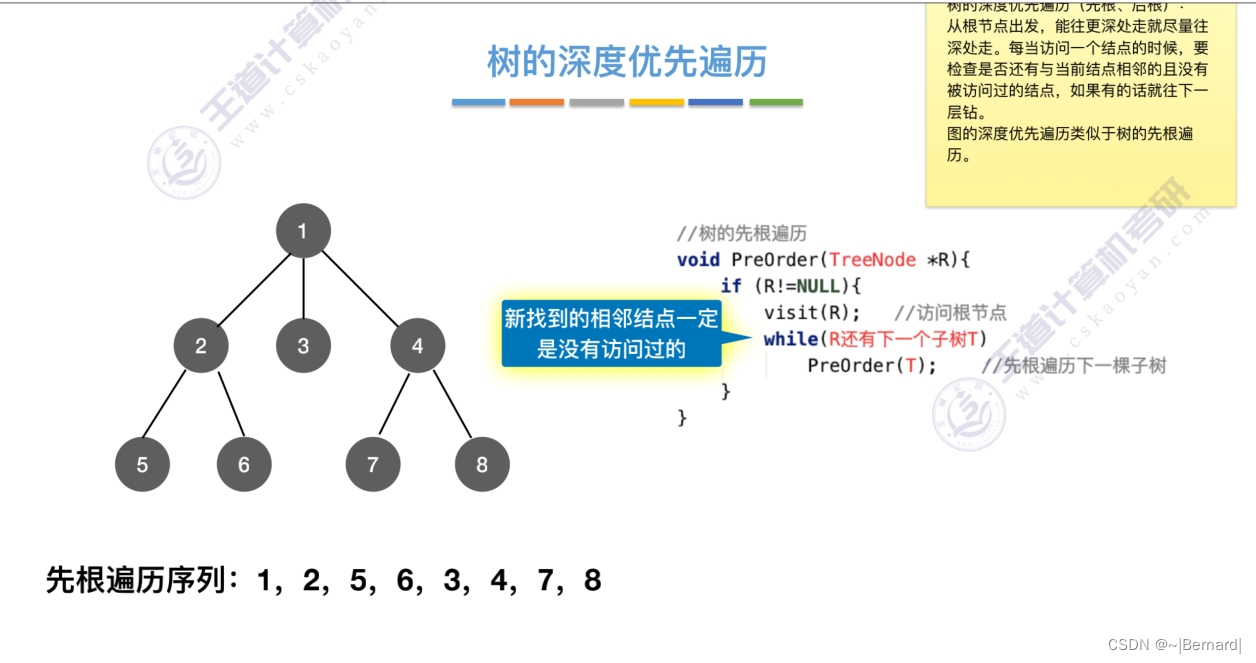
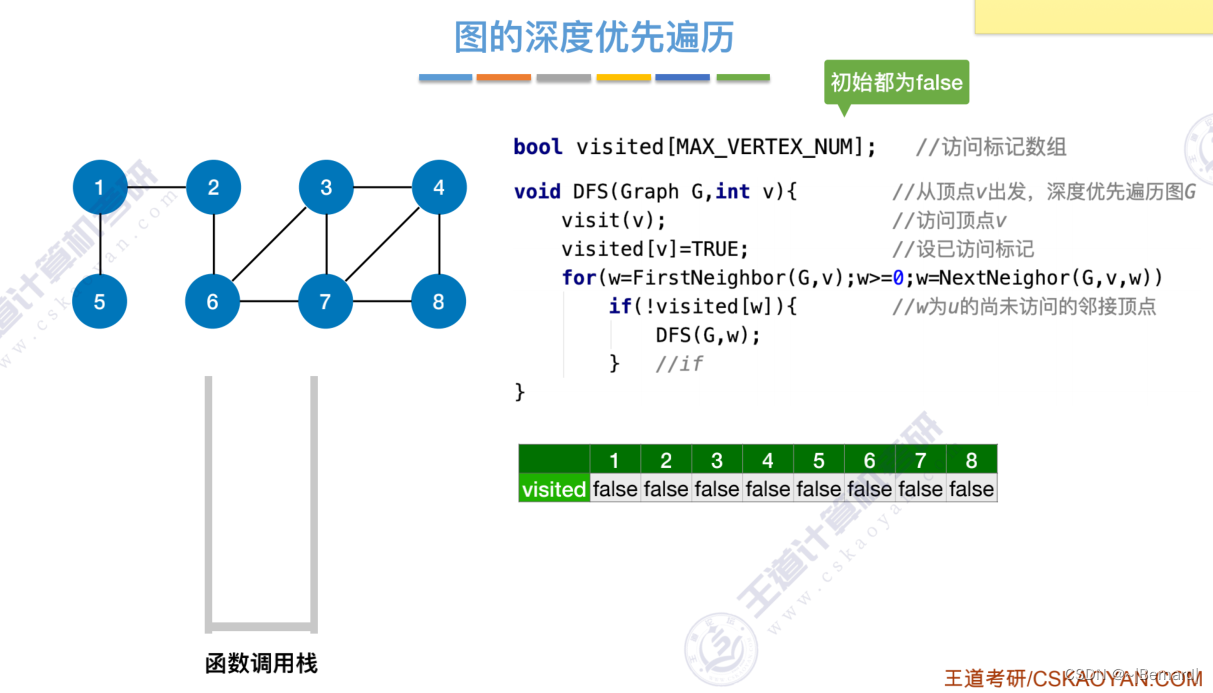
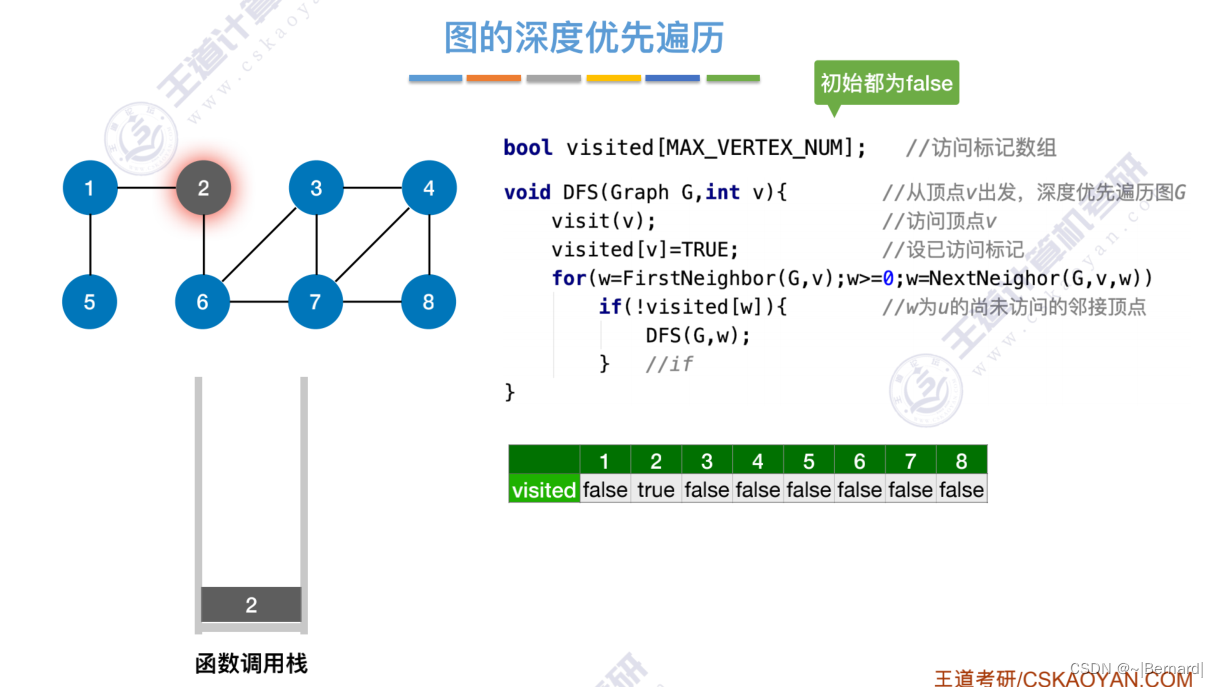
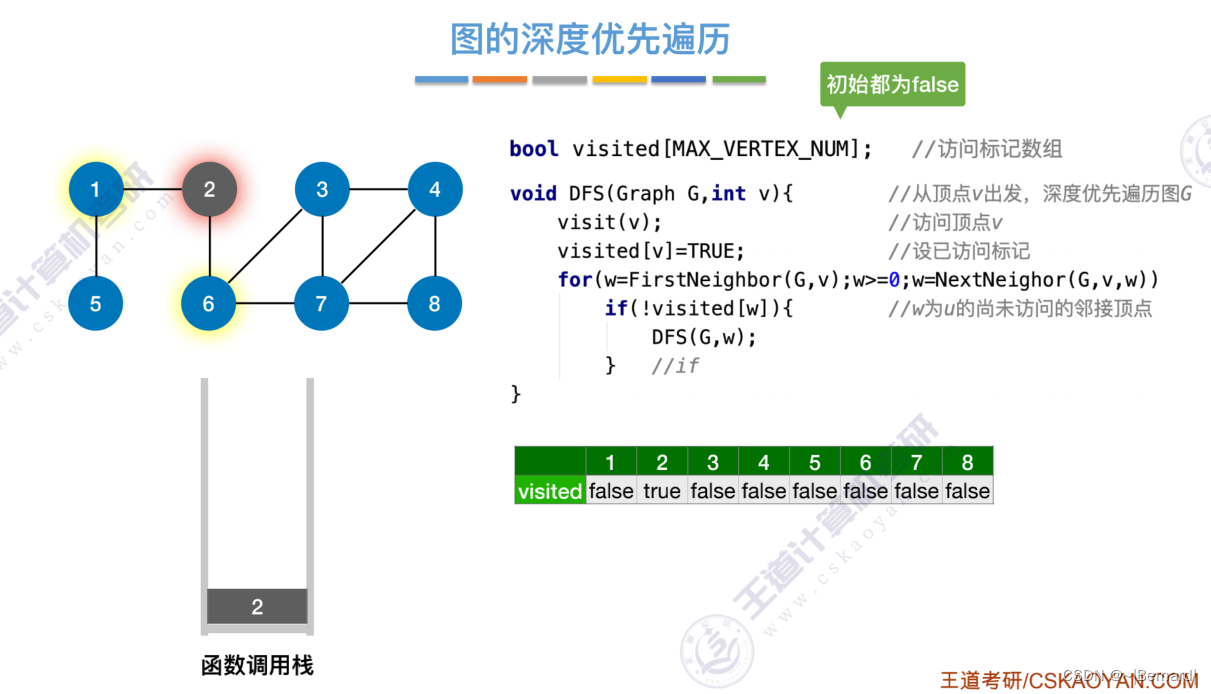
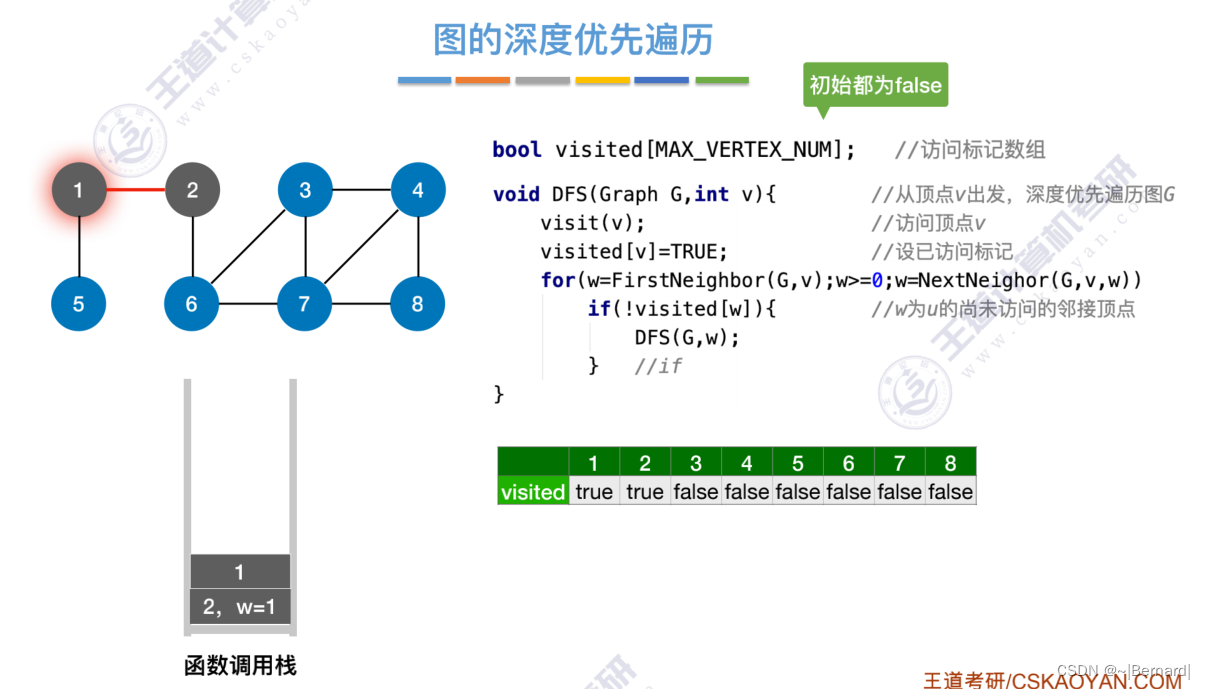
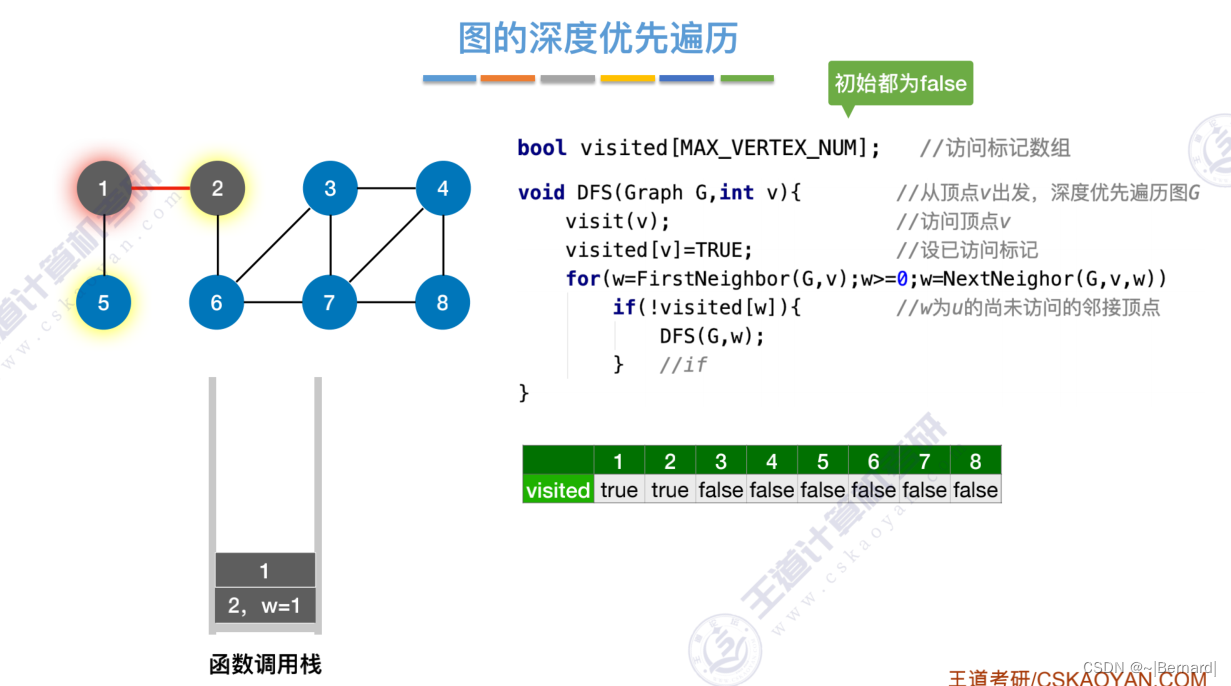
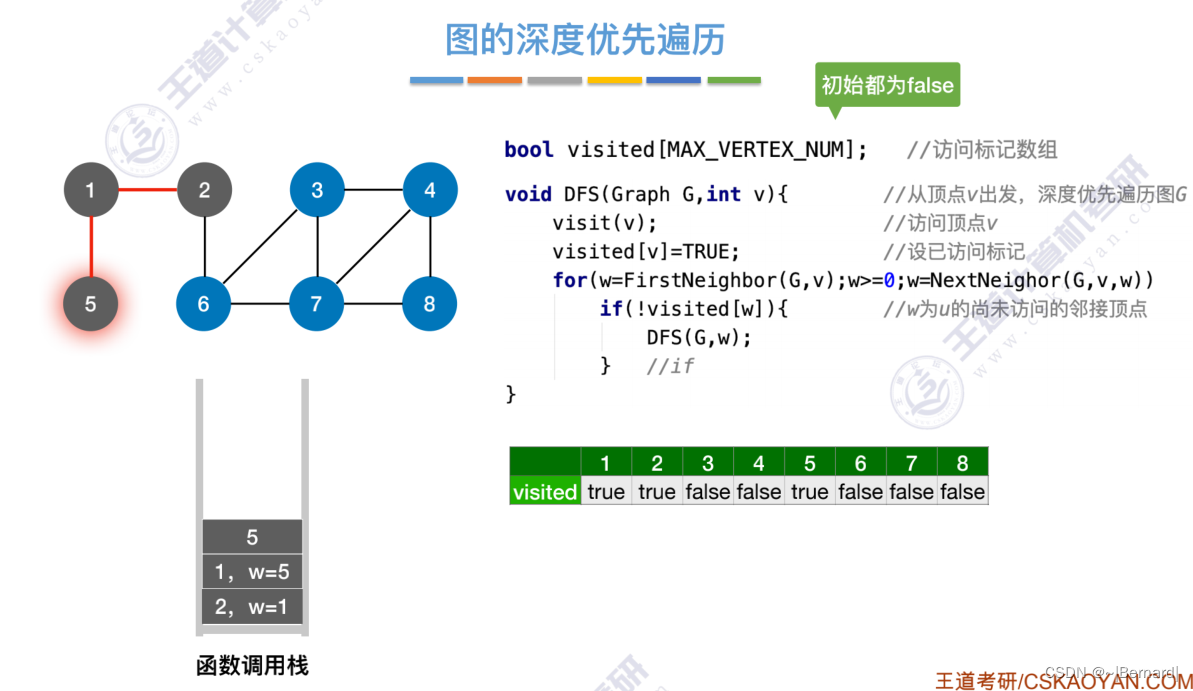
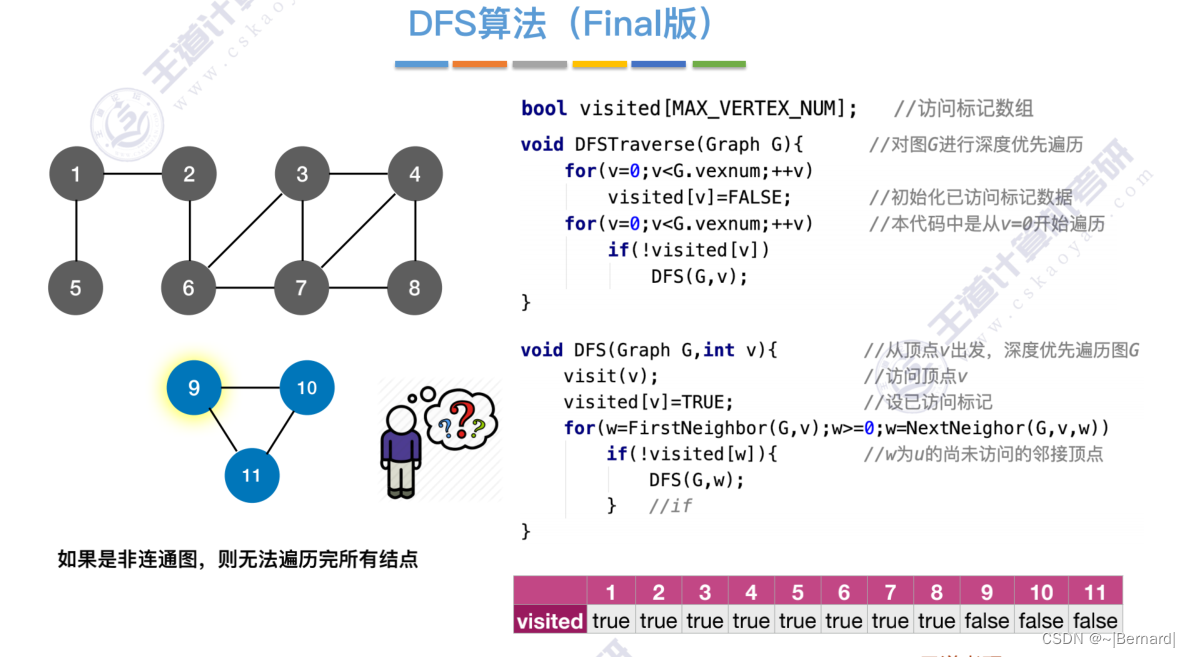
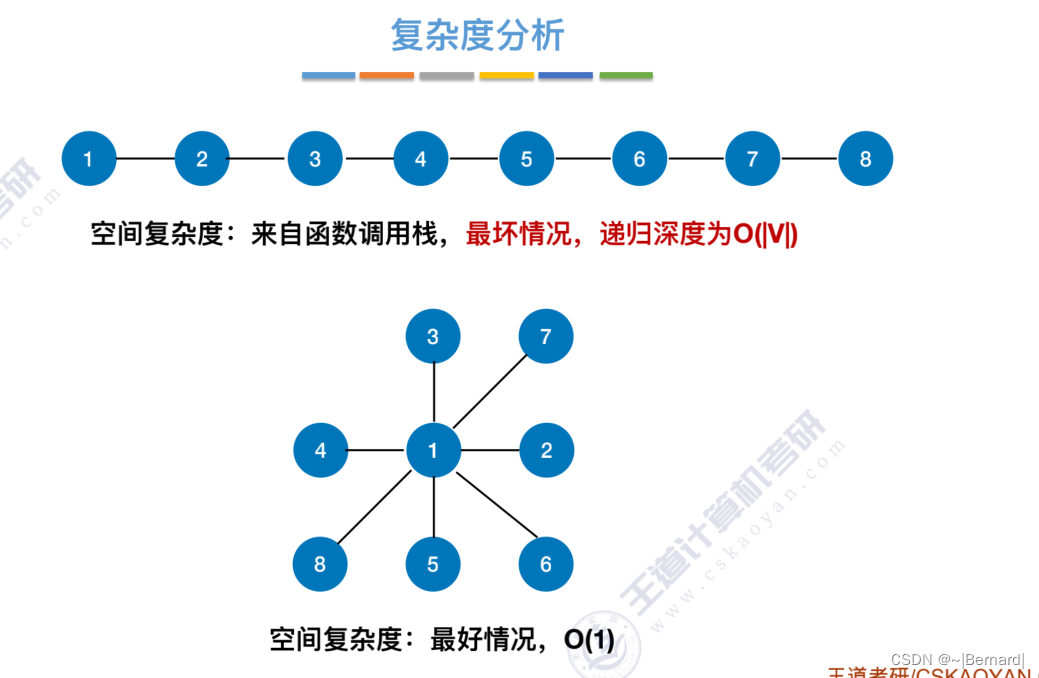
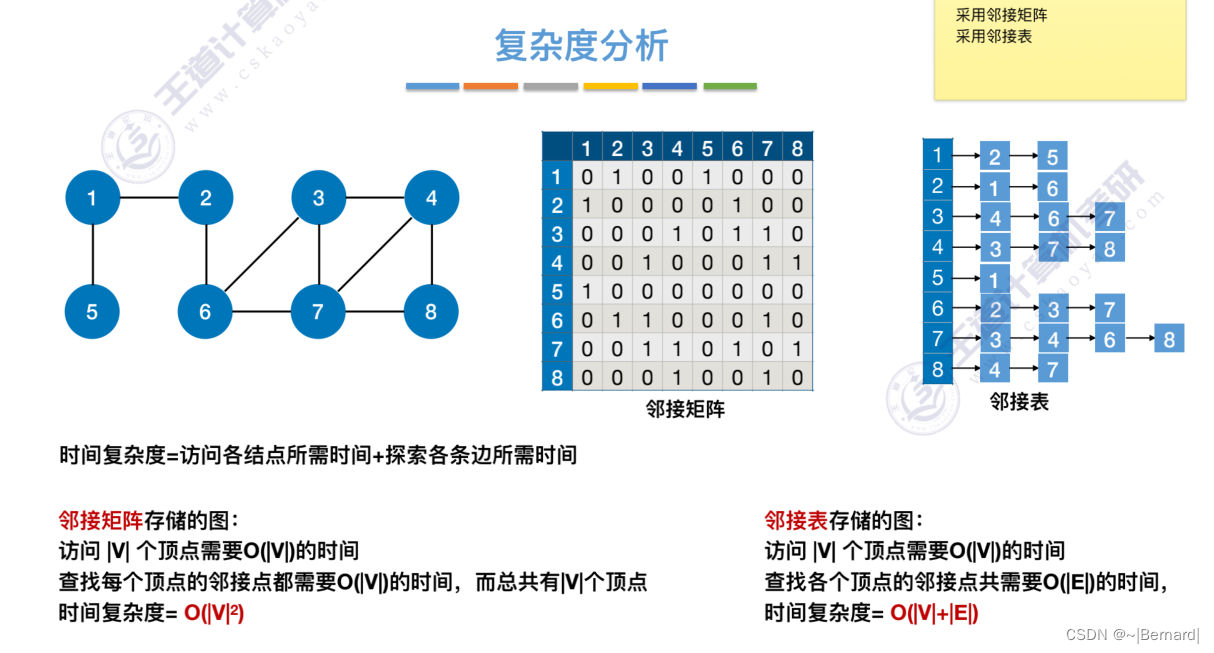
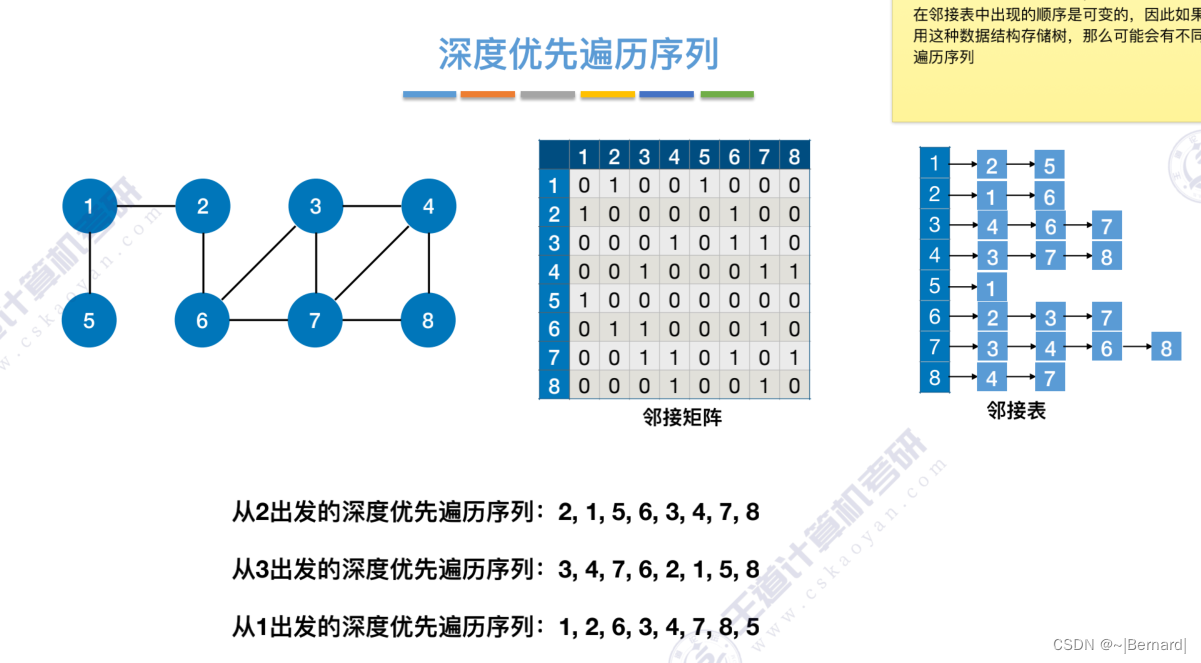
 6.3.2 图的深度优先遍历

 

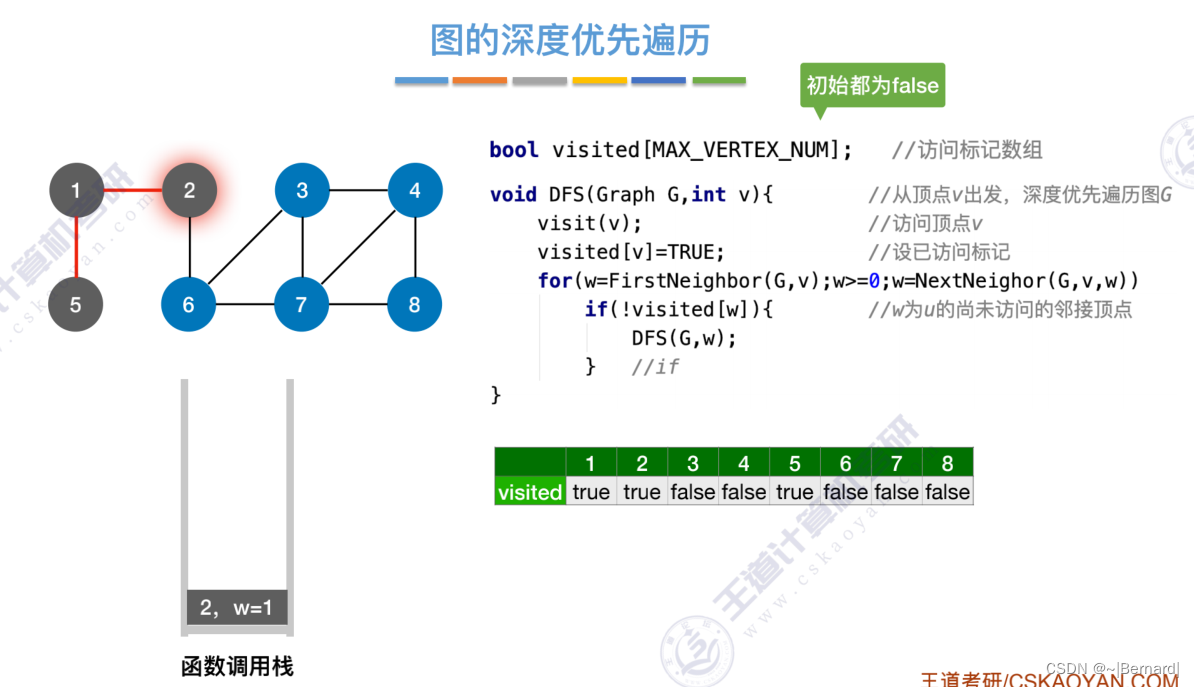
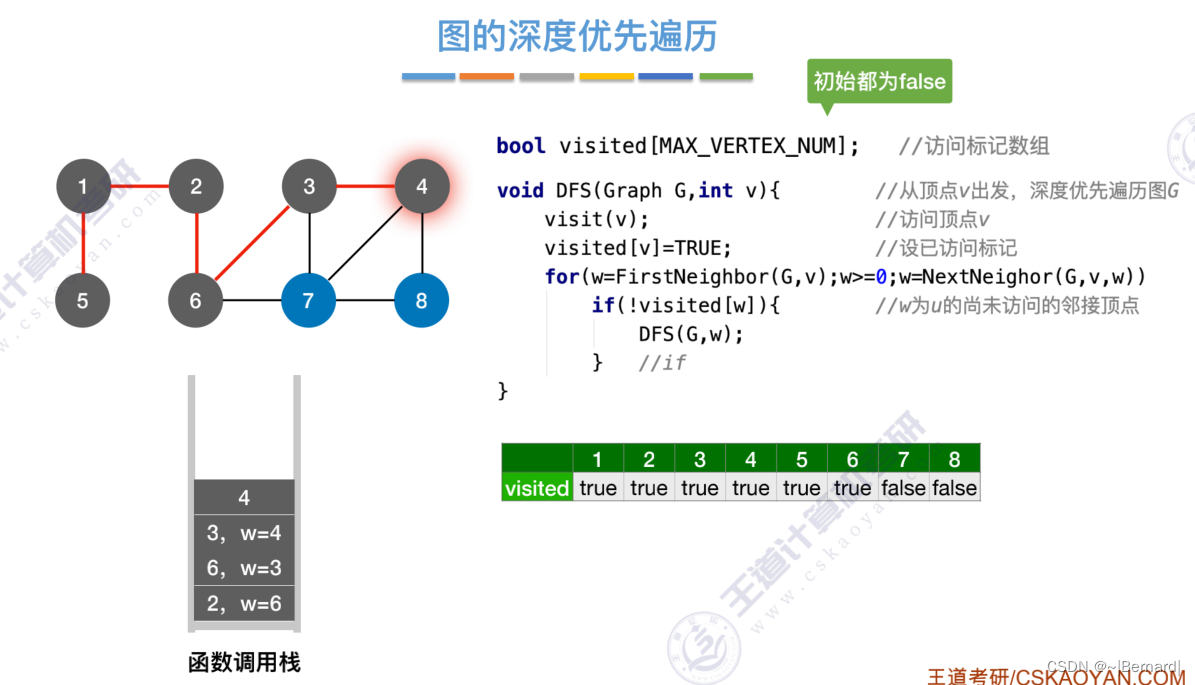
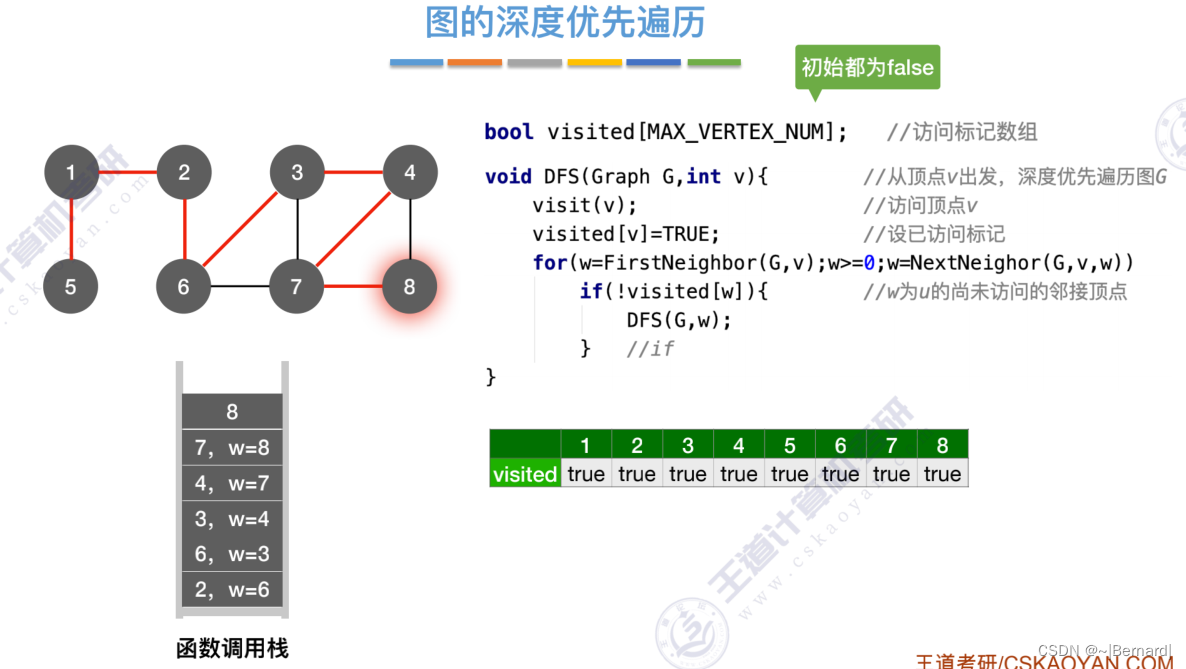
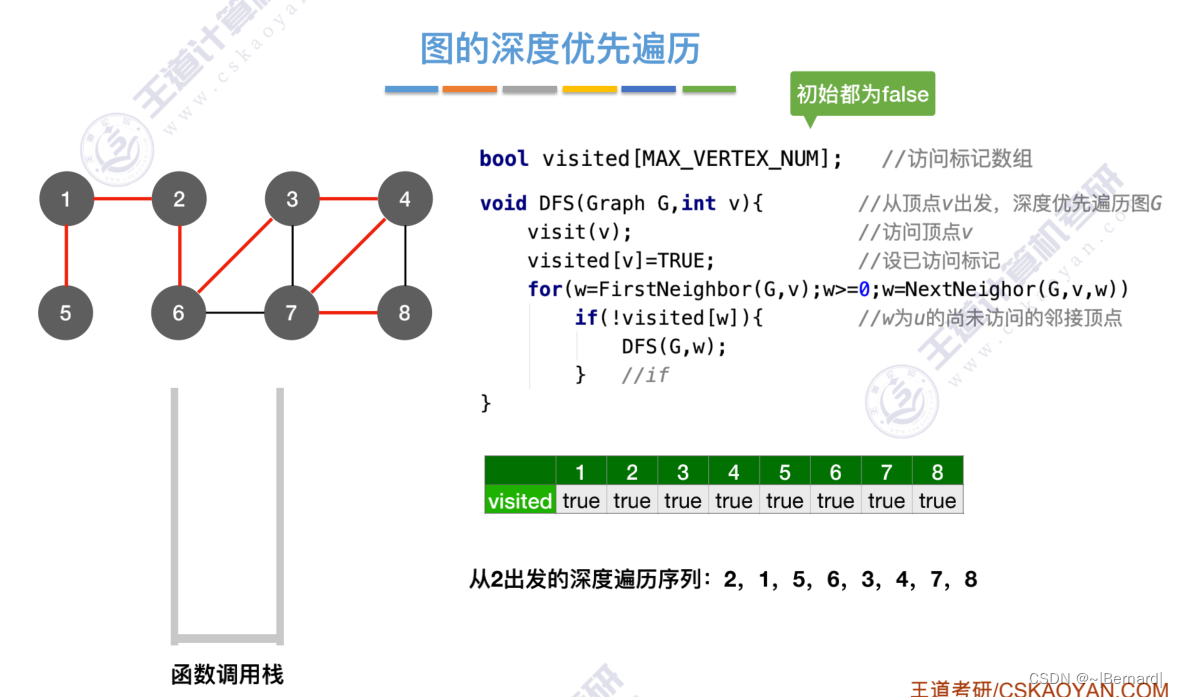
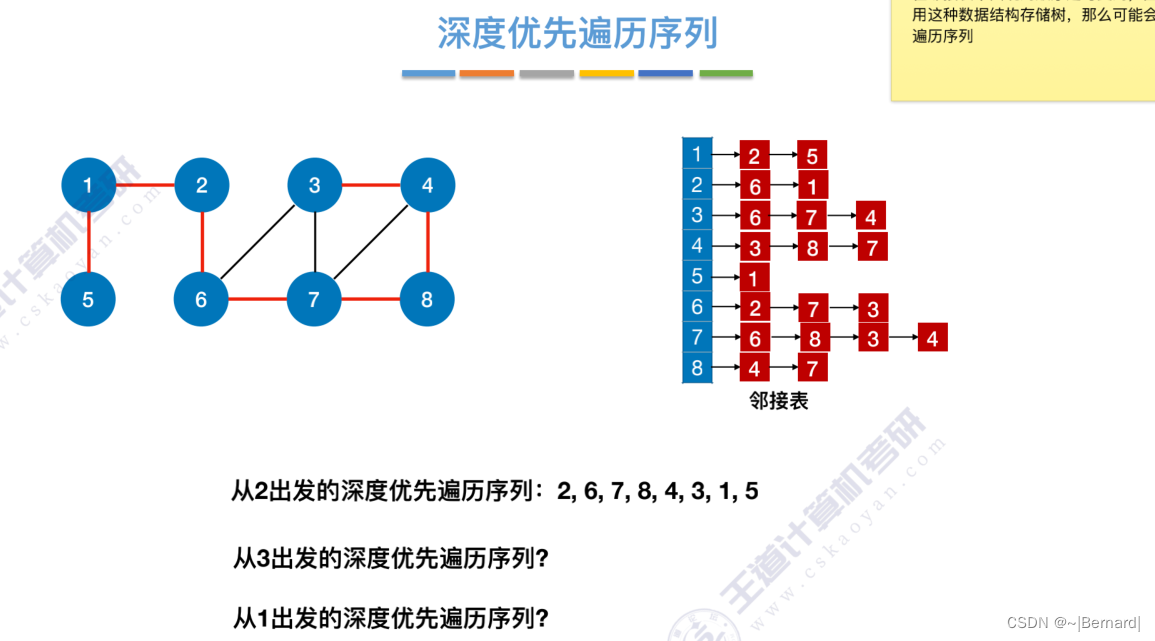
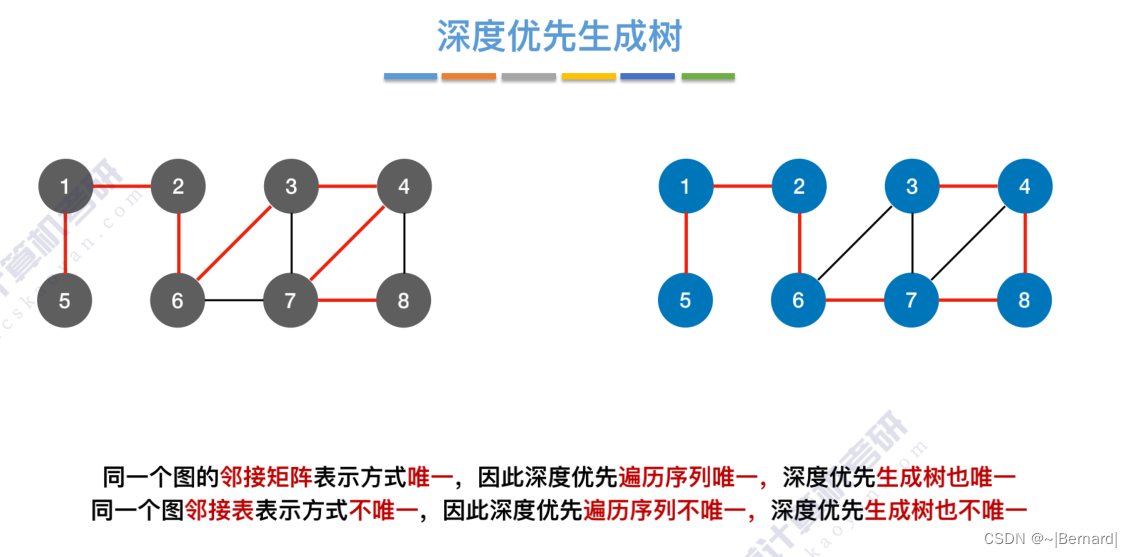
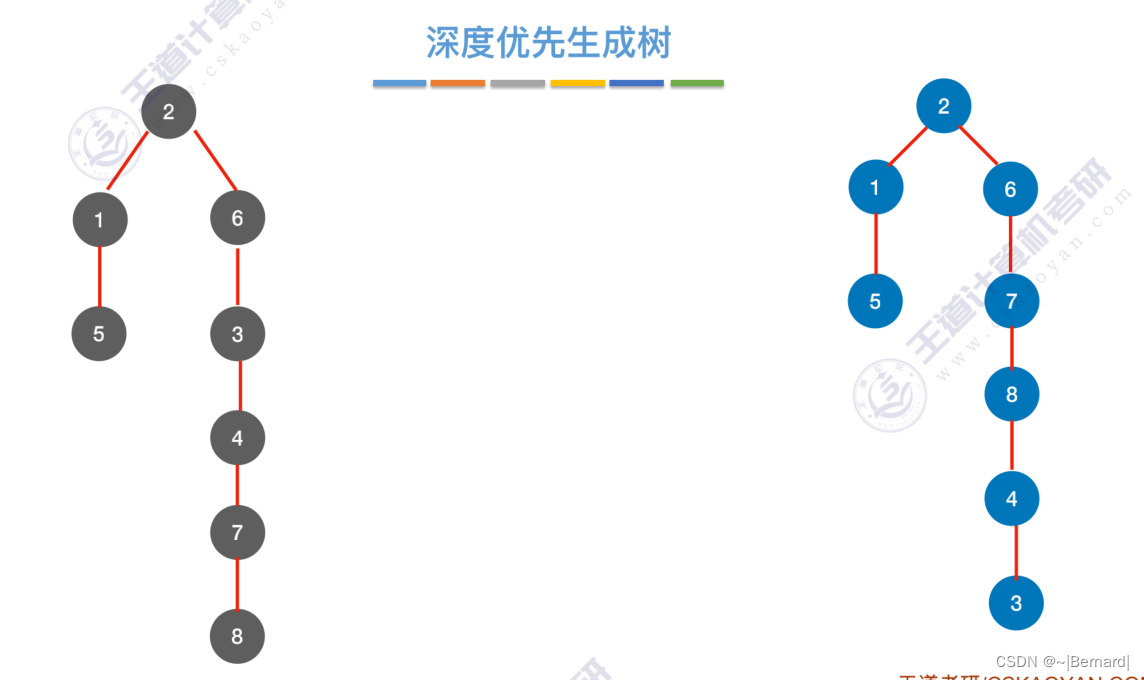
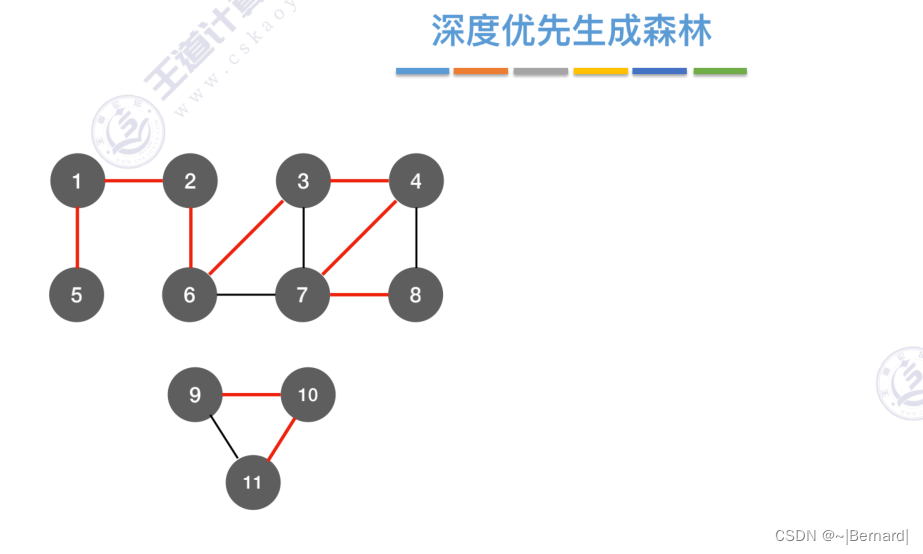
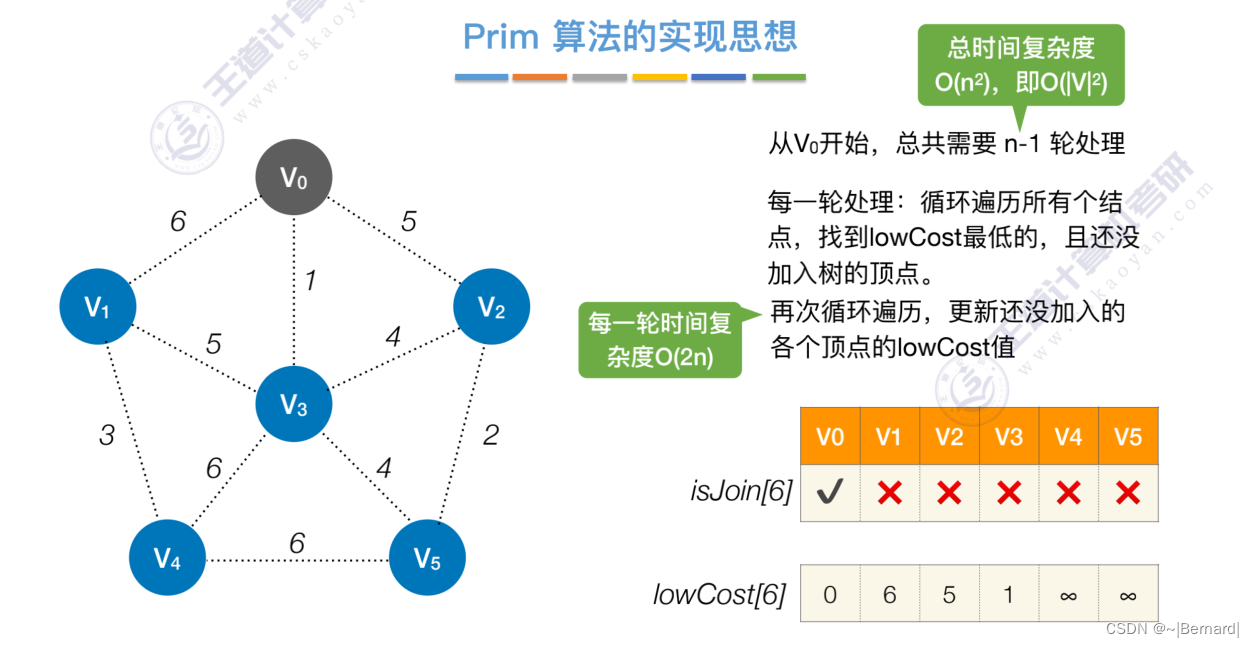
 6.4.1 最小生成树

 

 

 

 

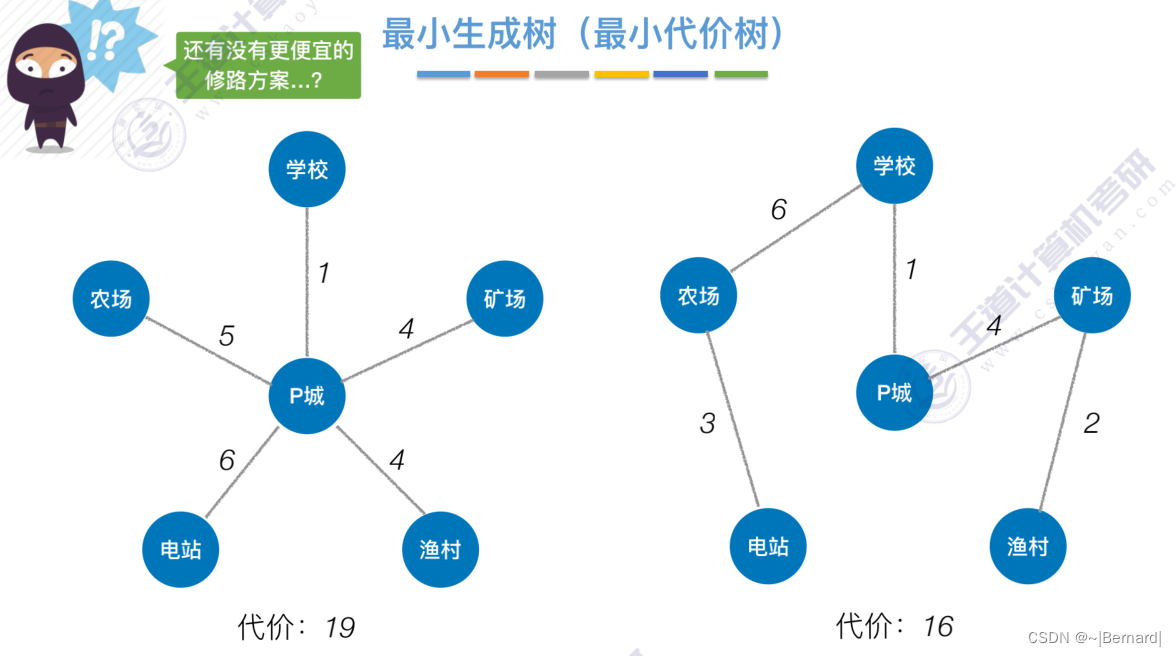
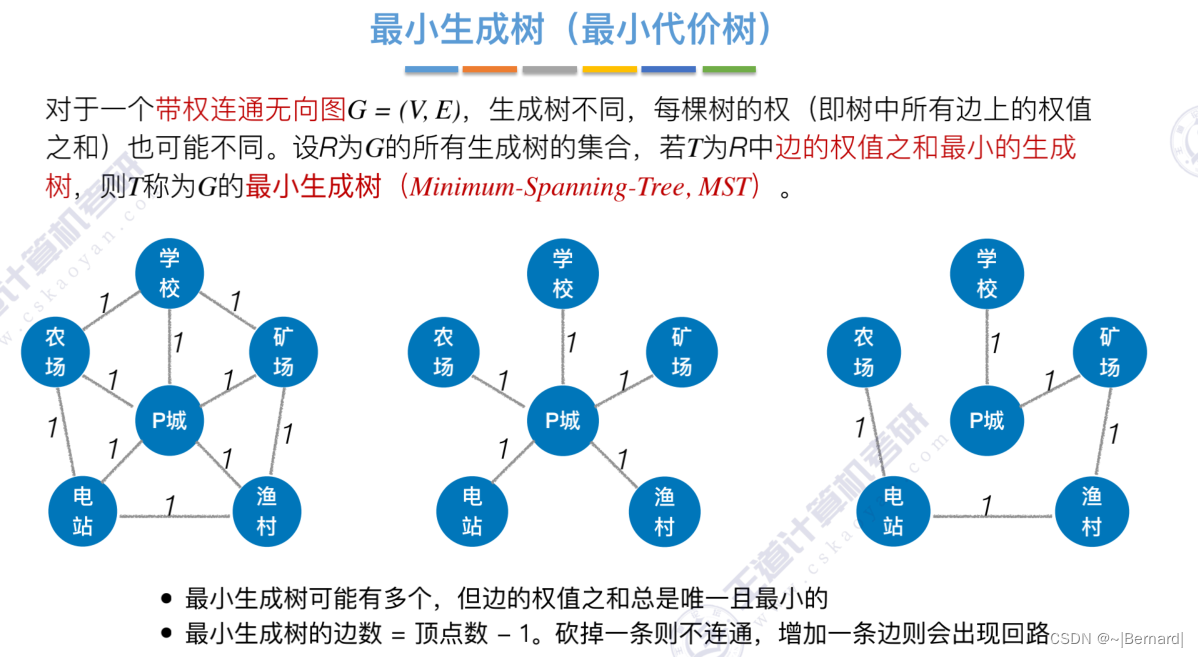
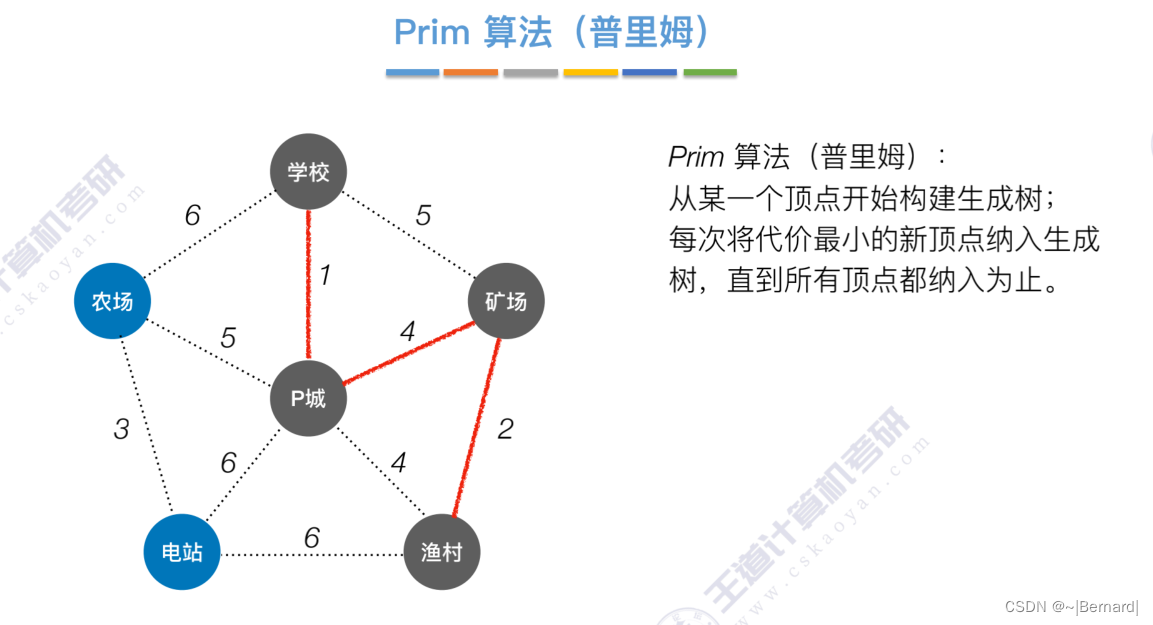
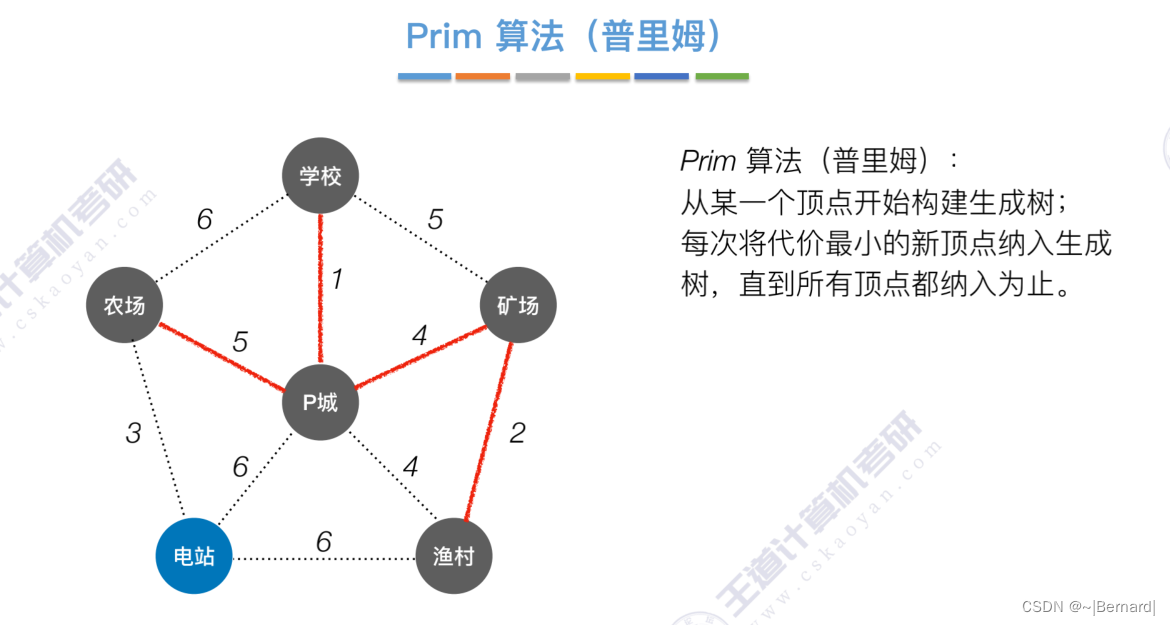
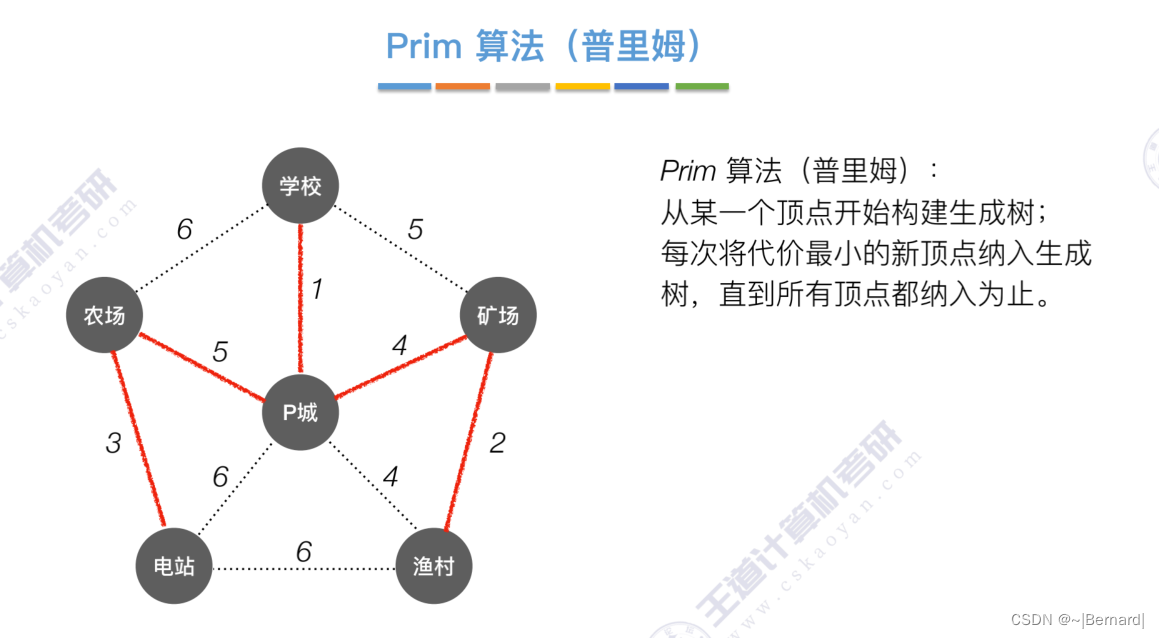
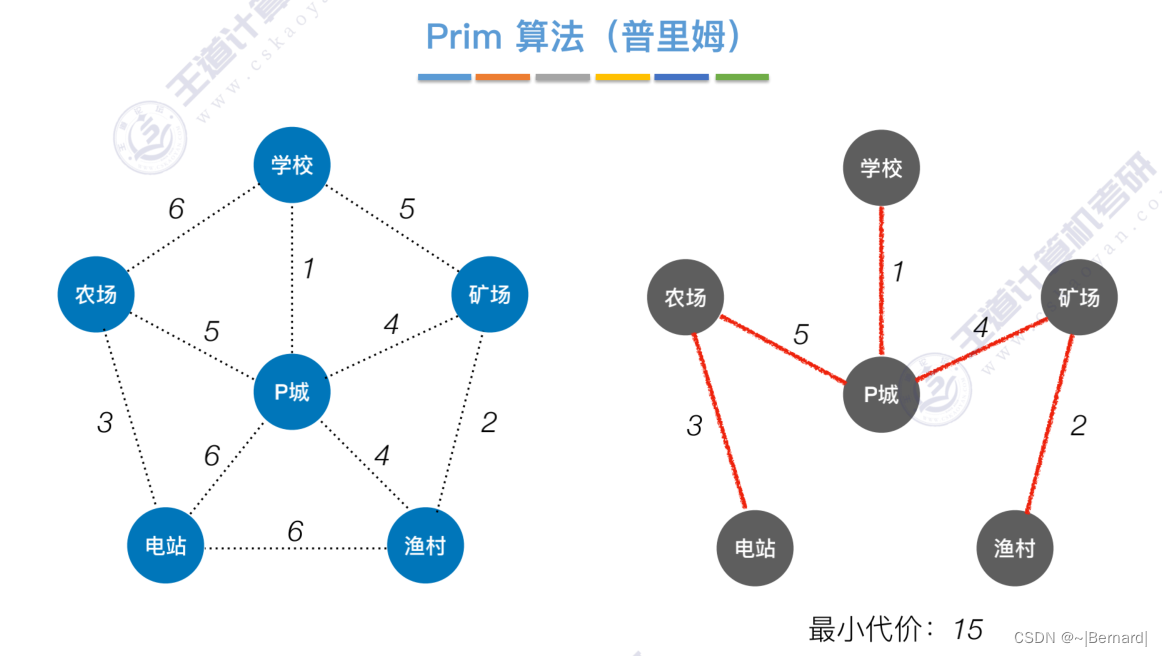
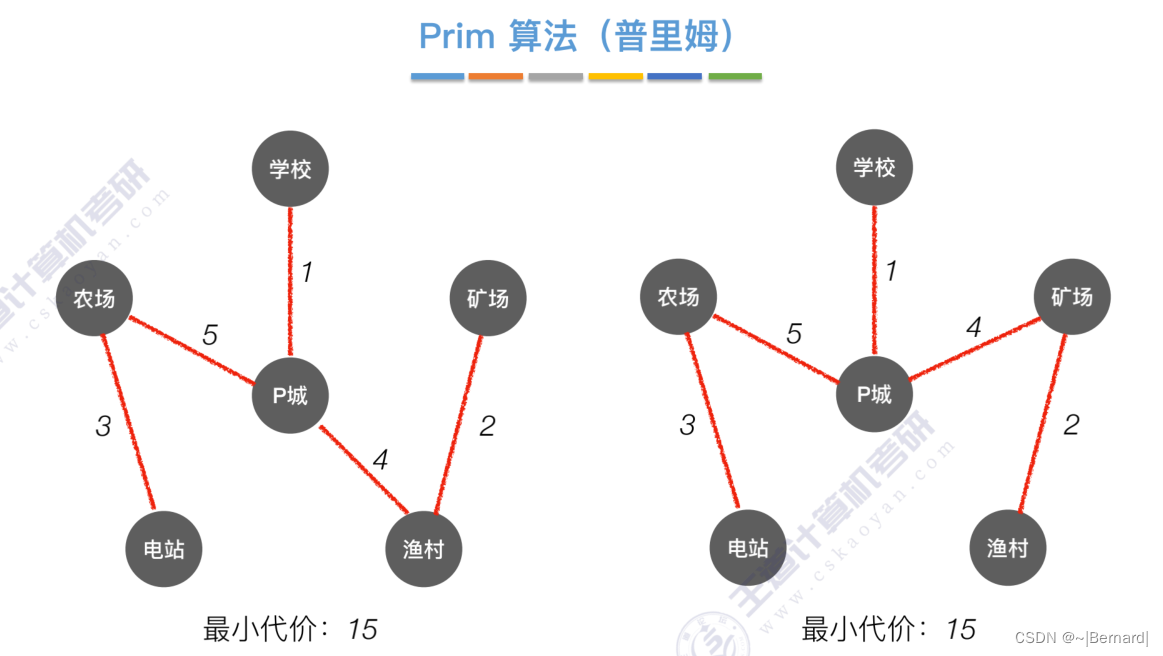
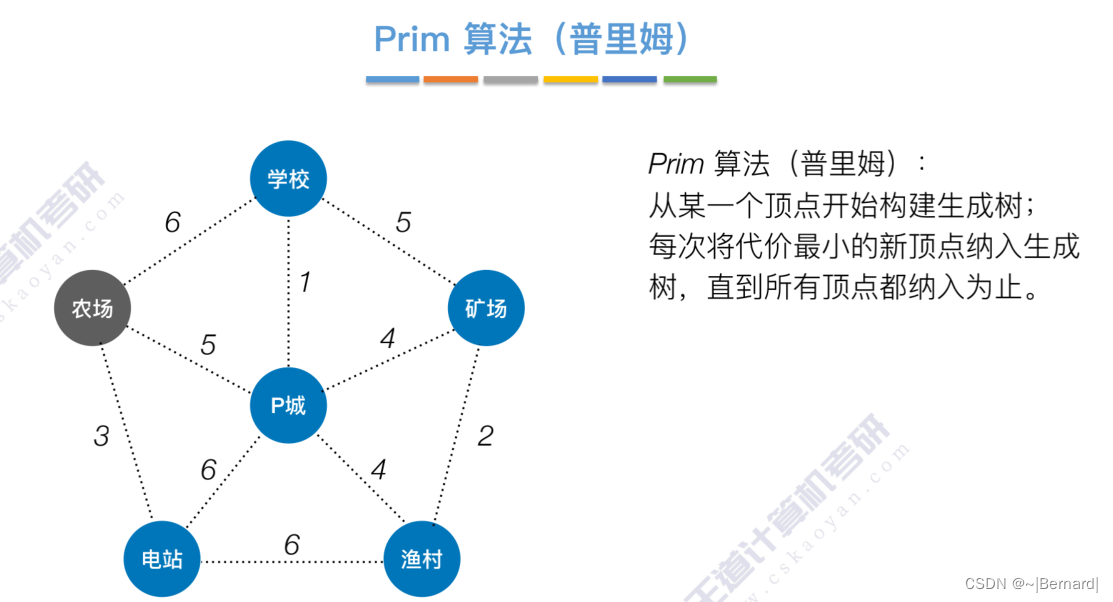
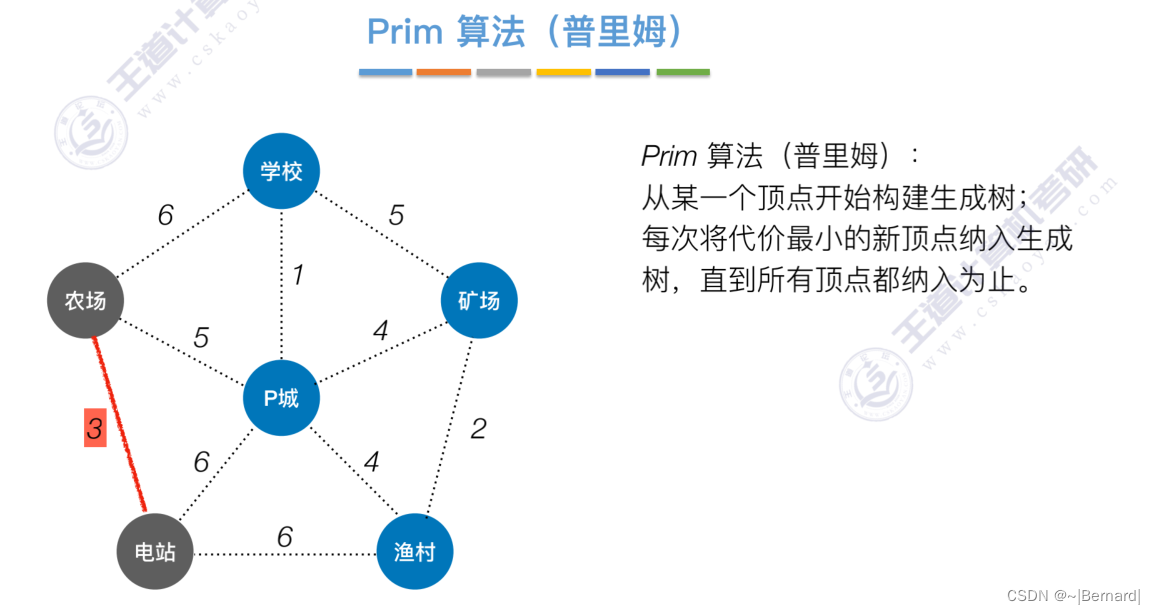
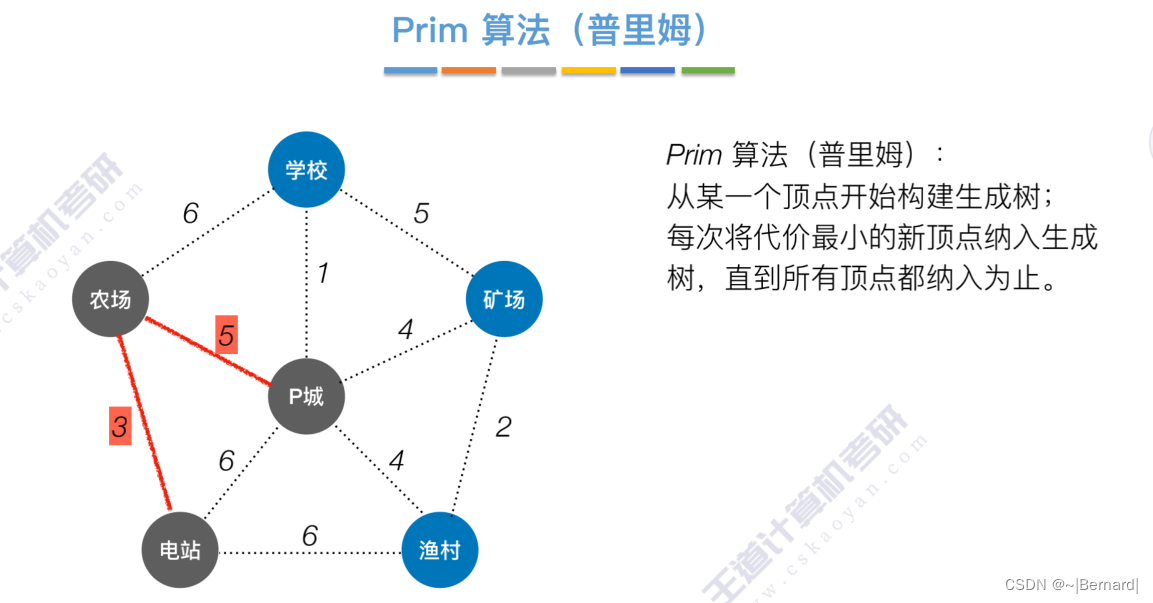
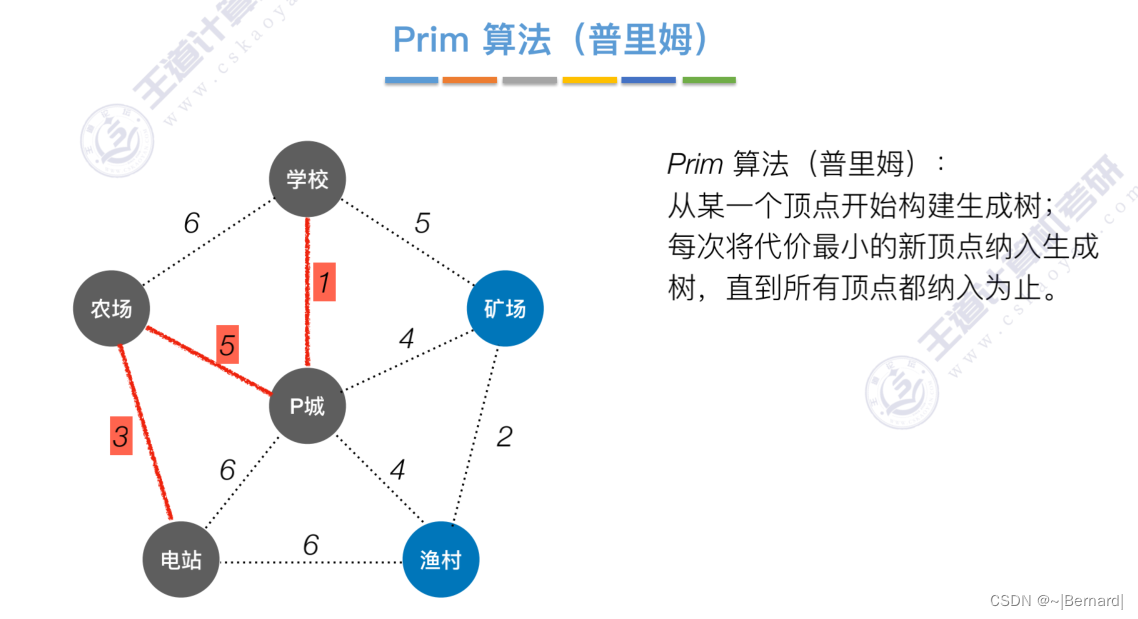
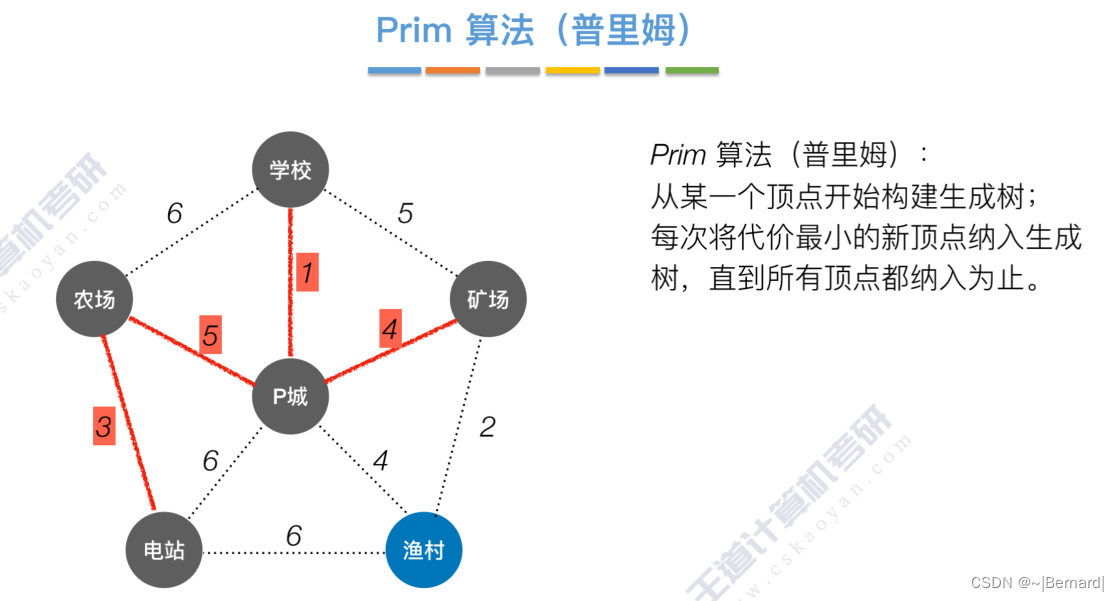
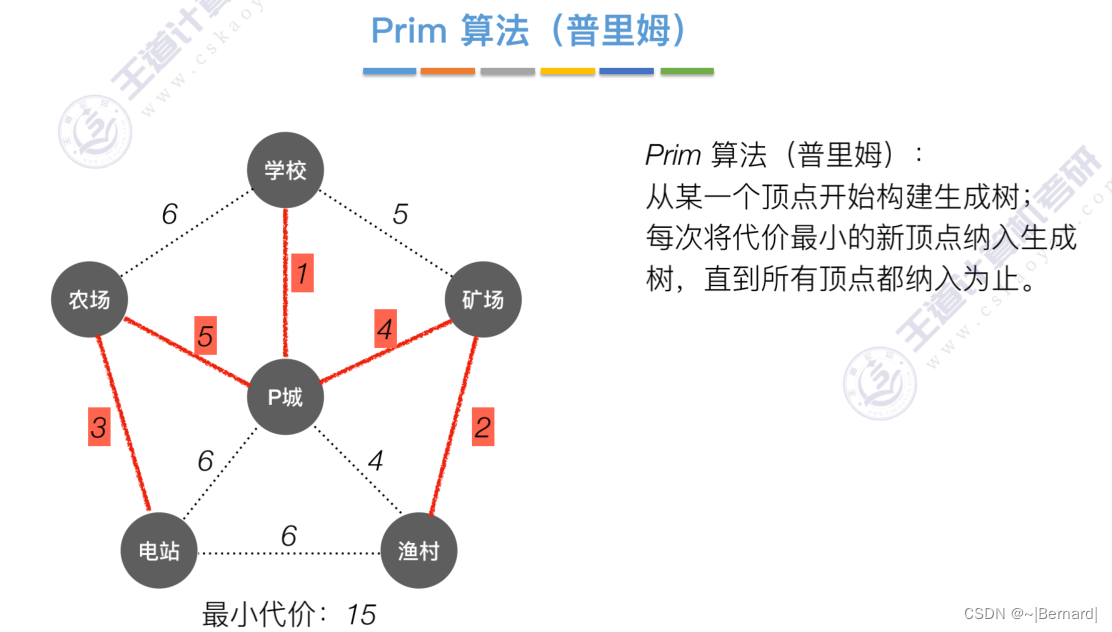
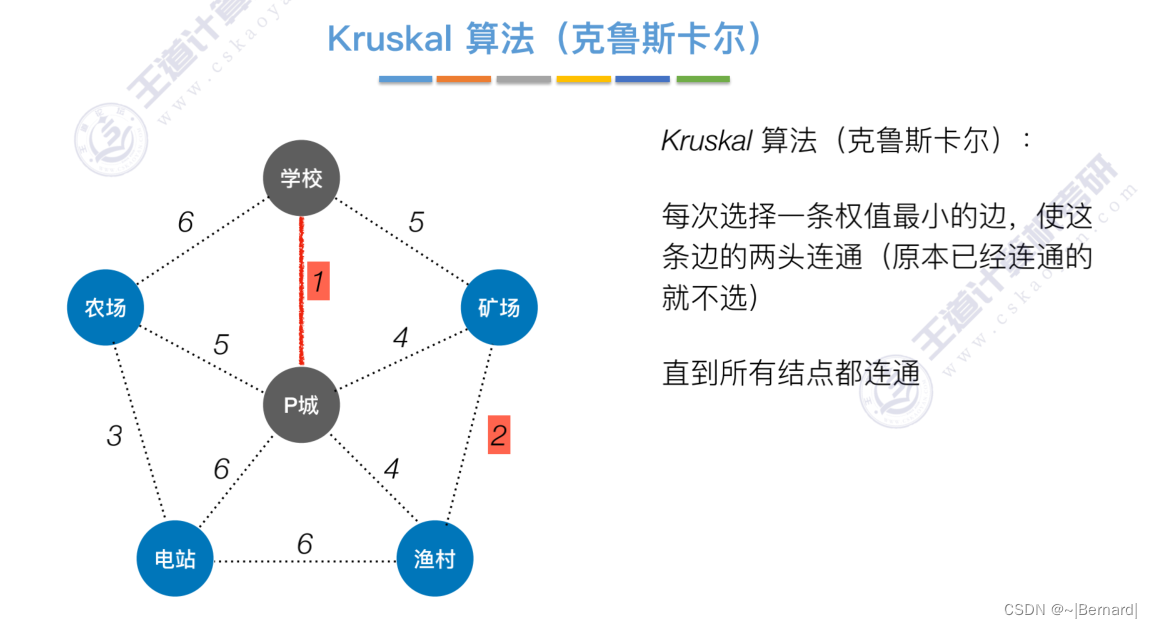
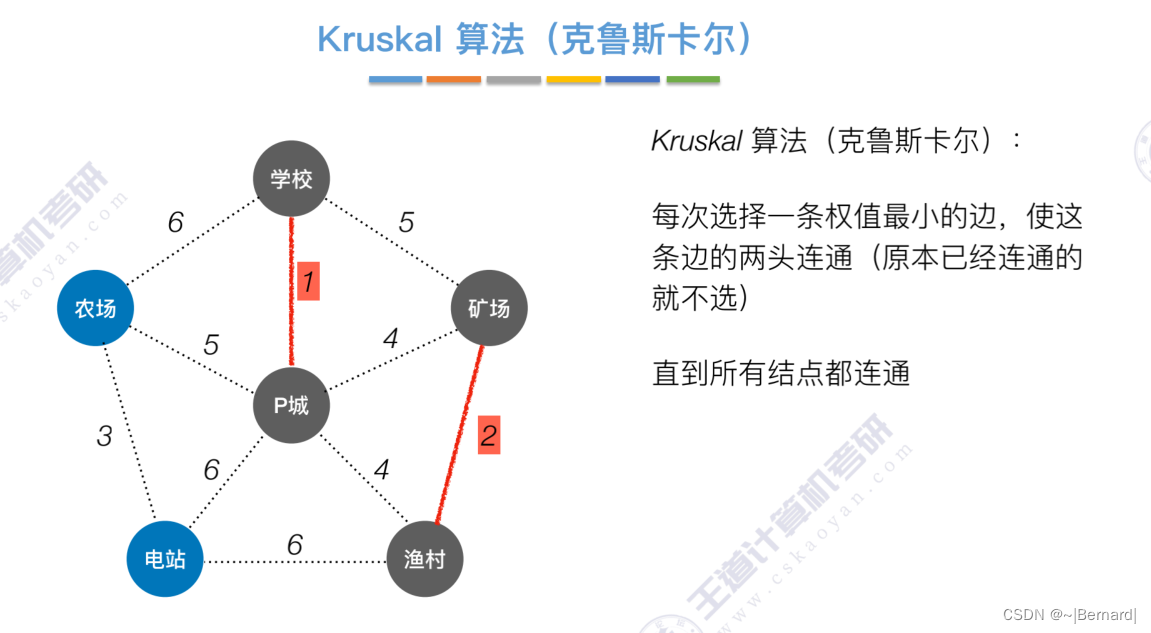
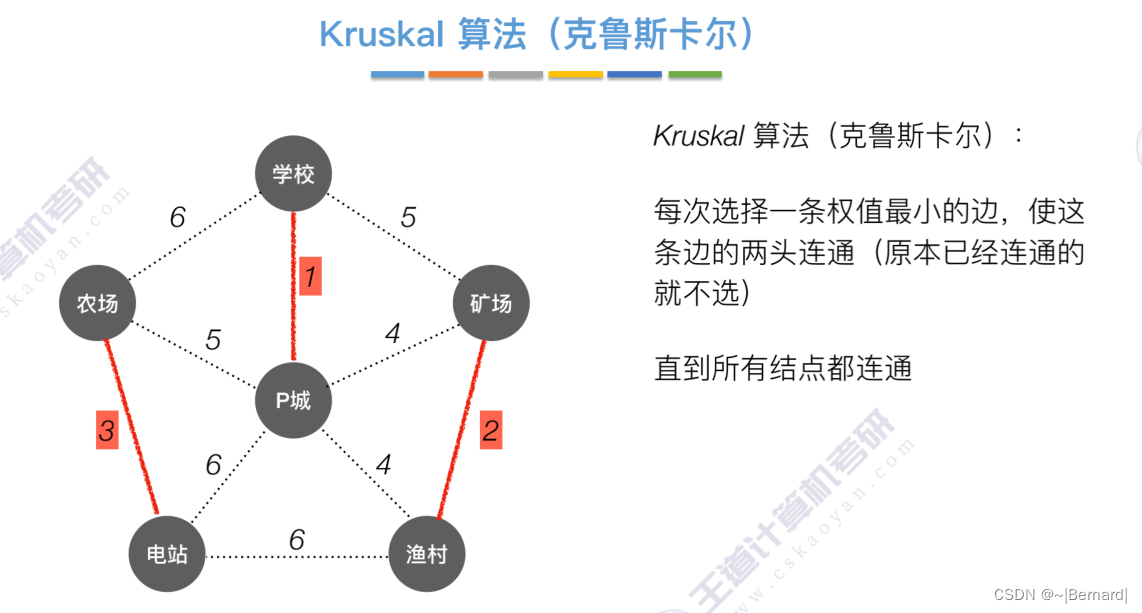
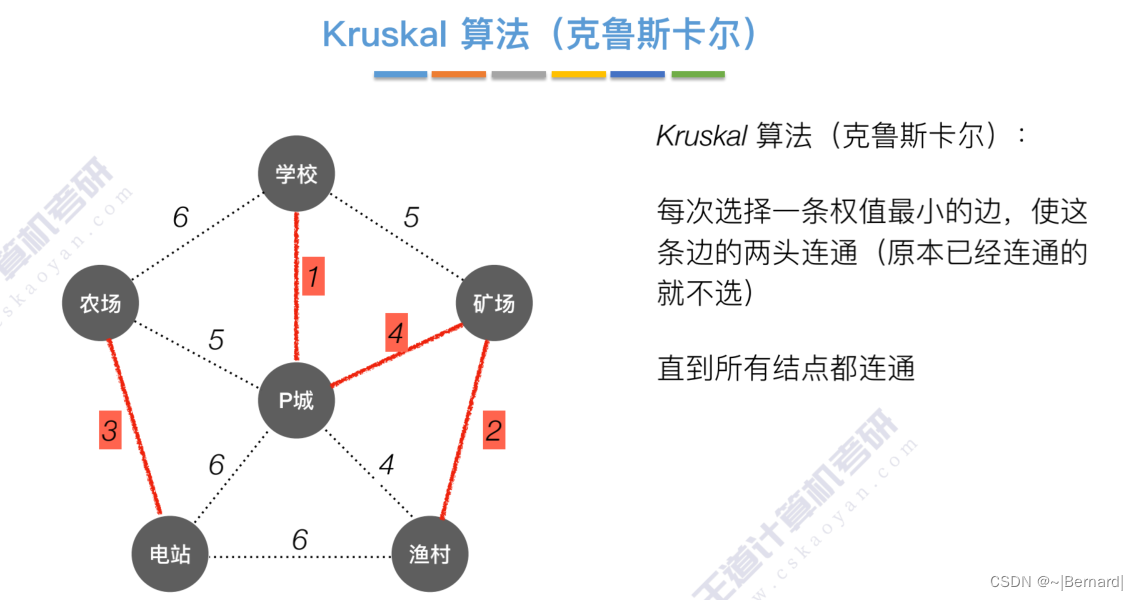
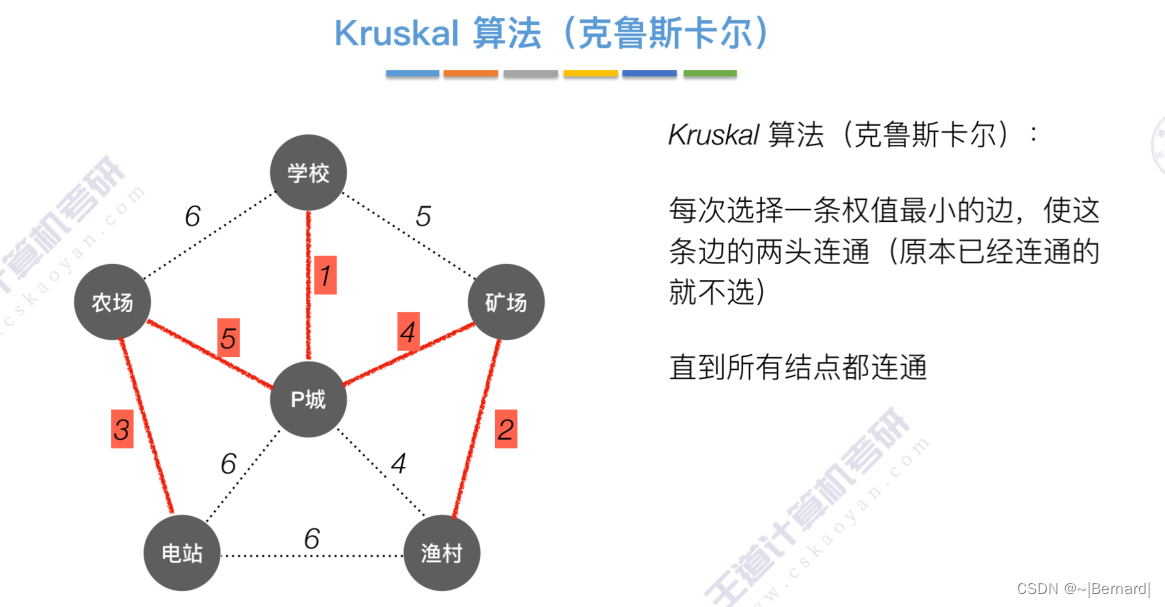
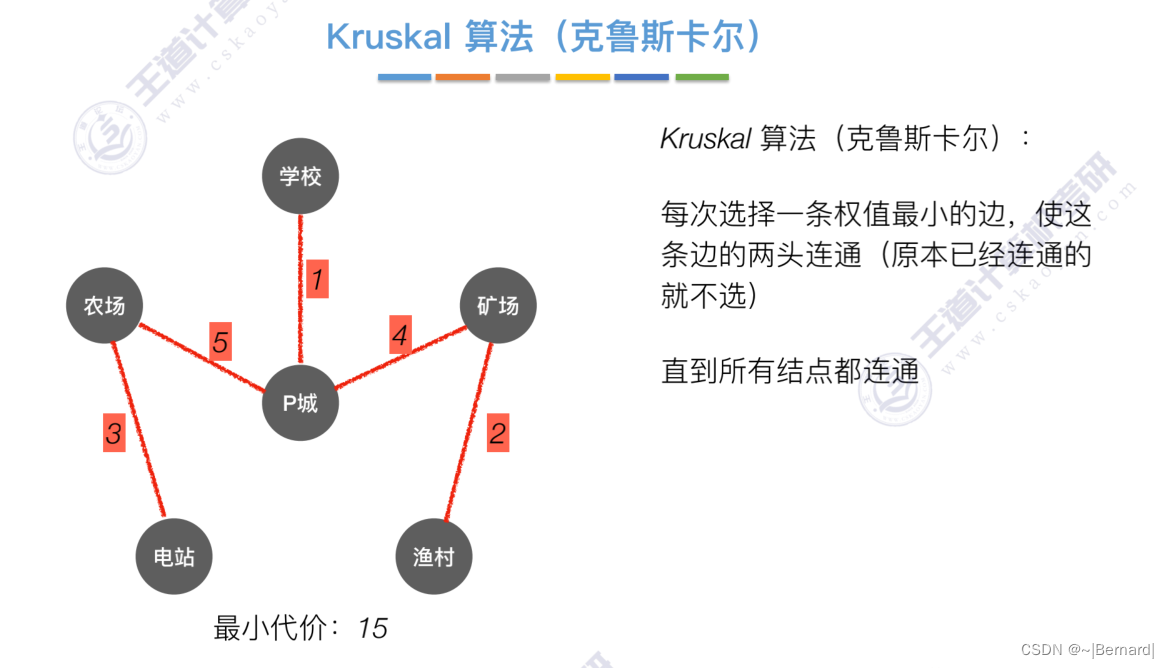
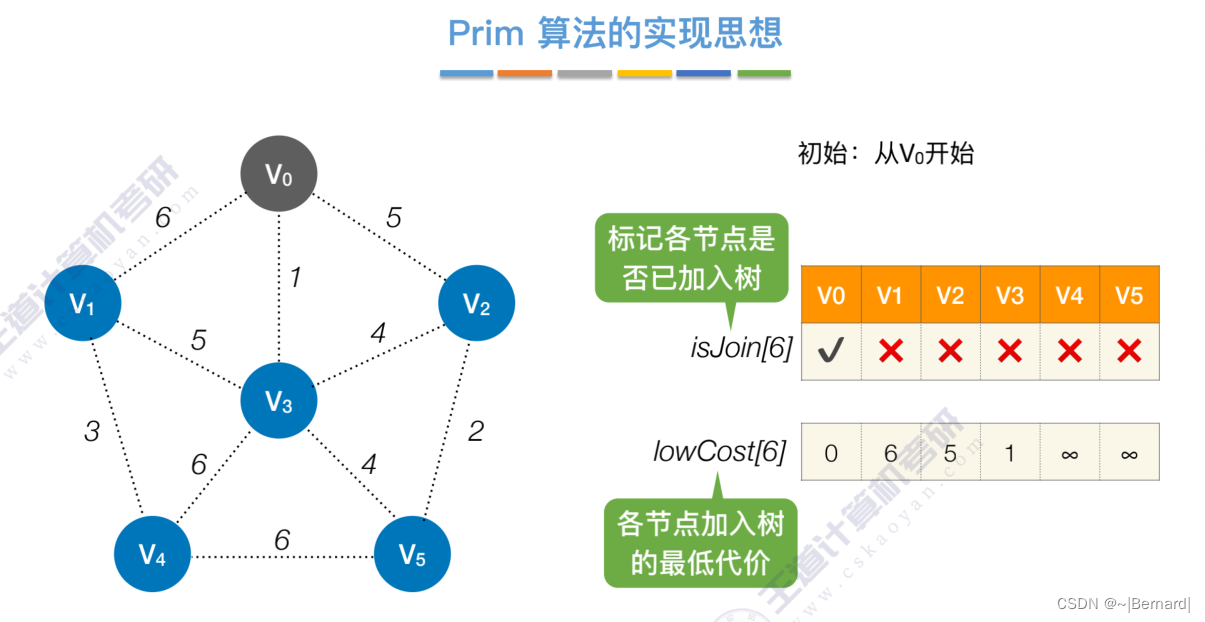
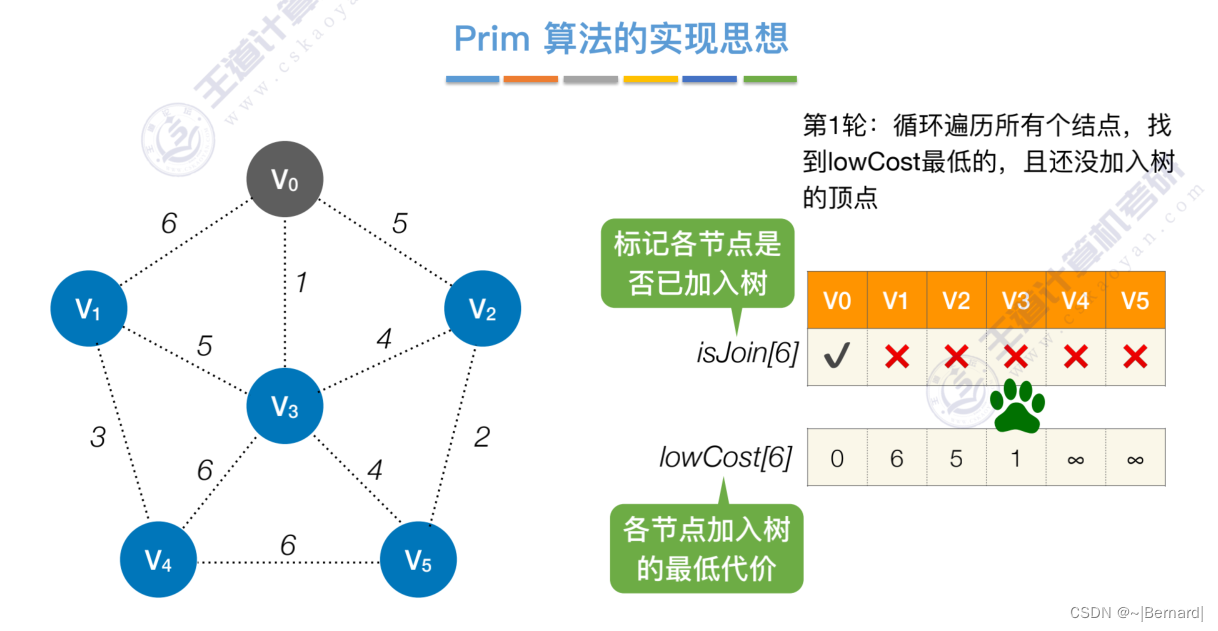
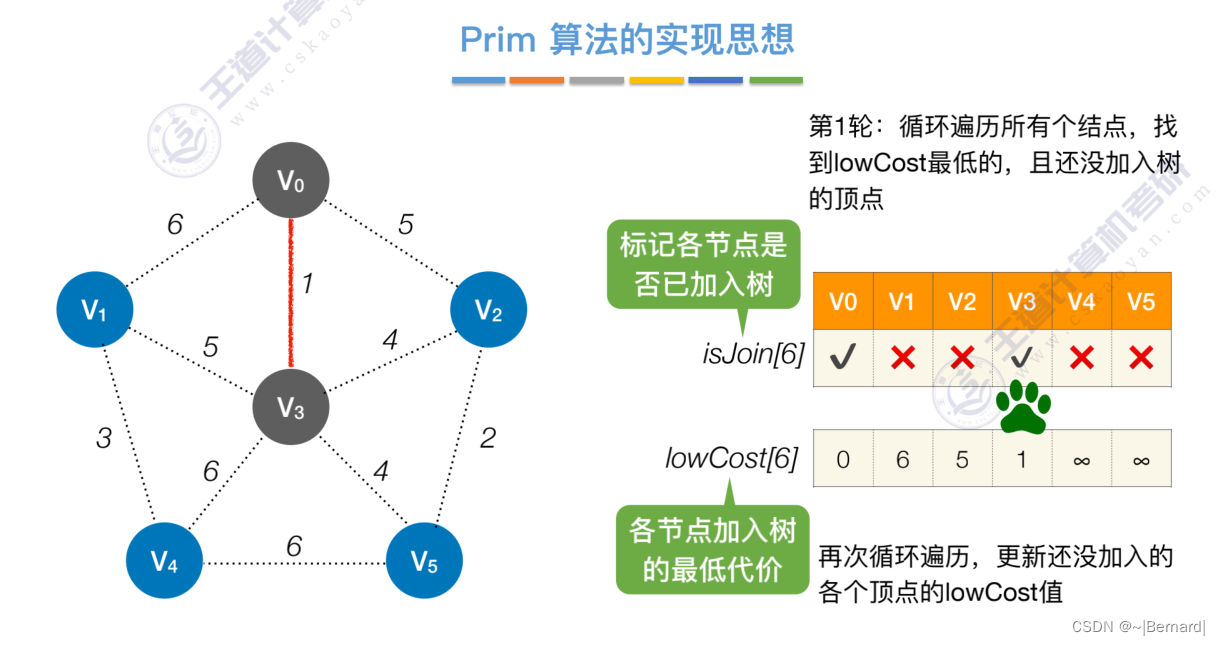
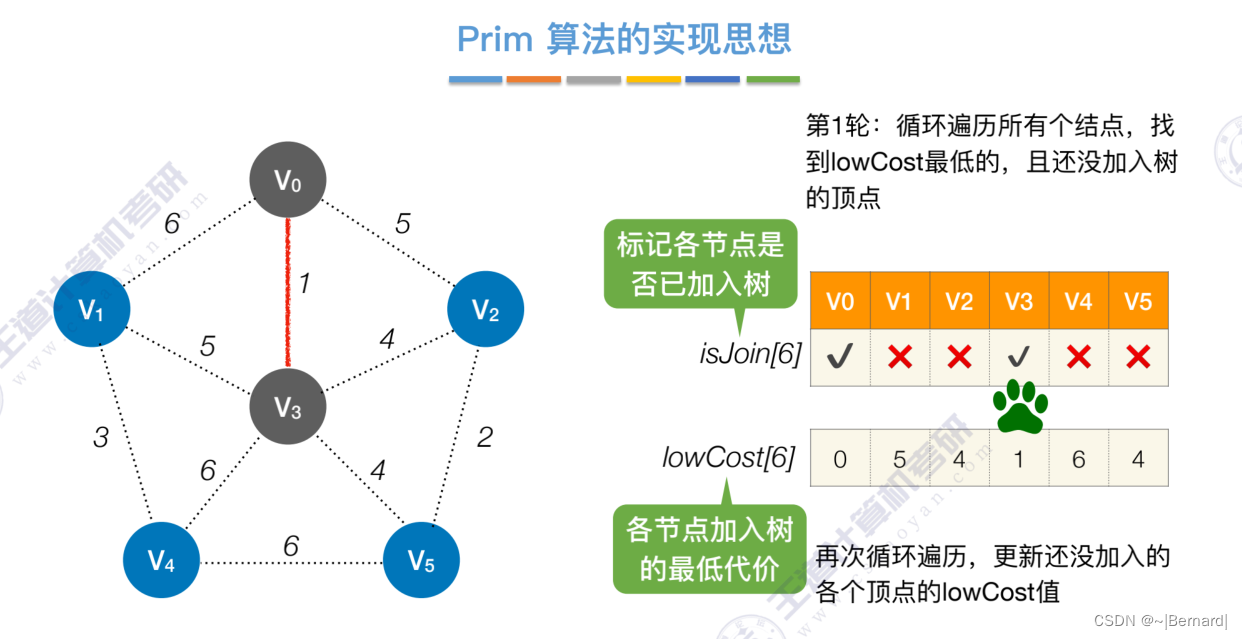
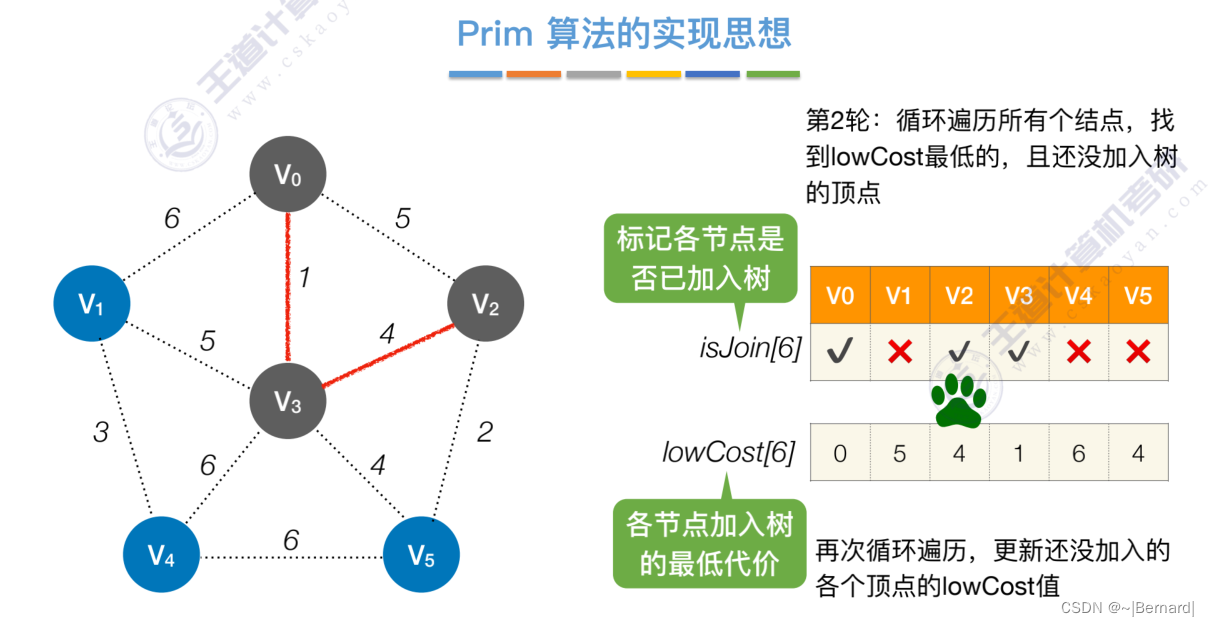
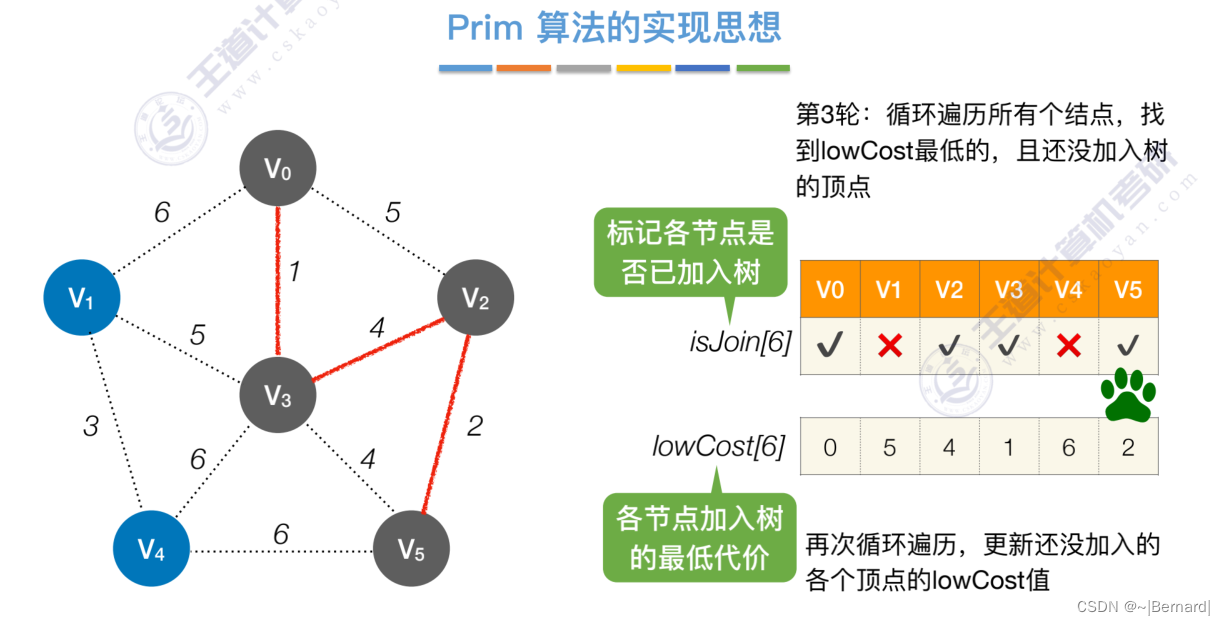
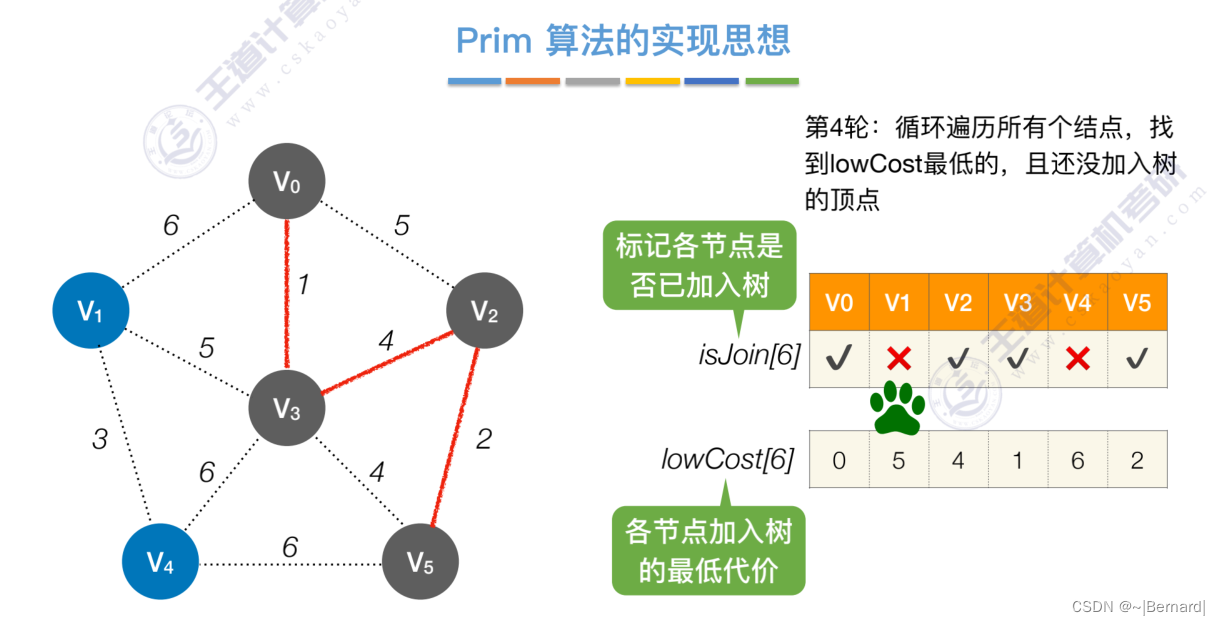
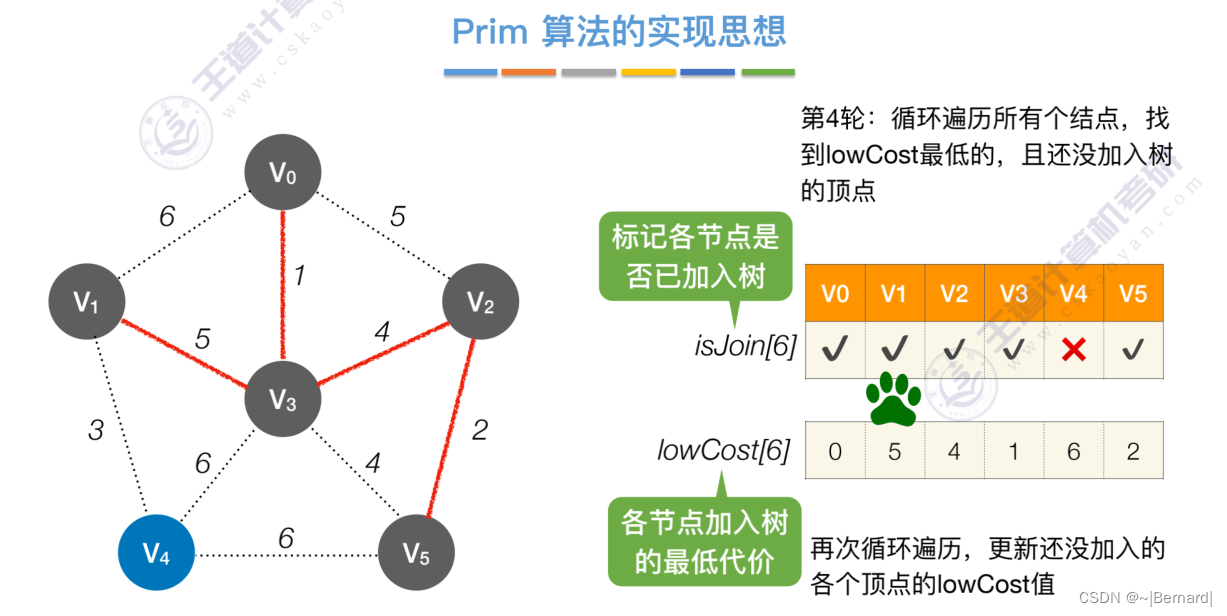
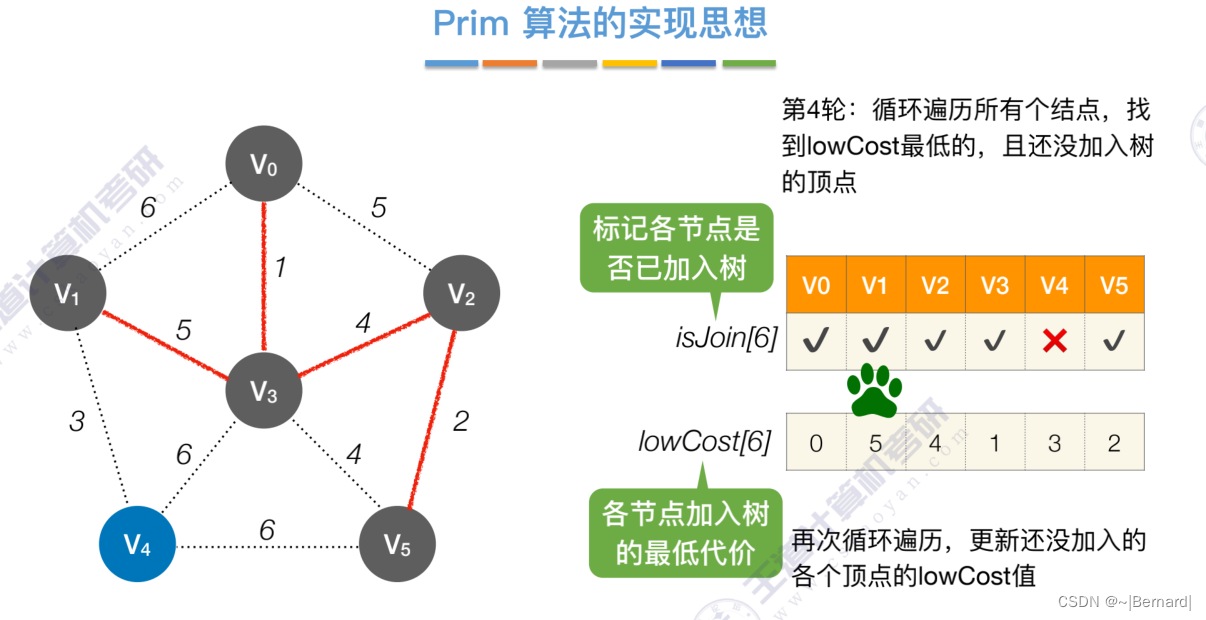
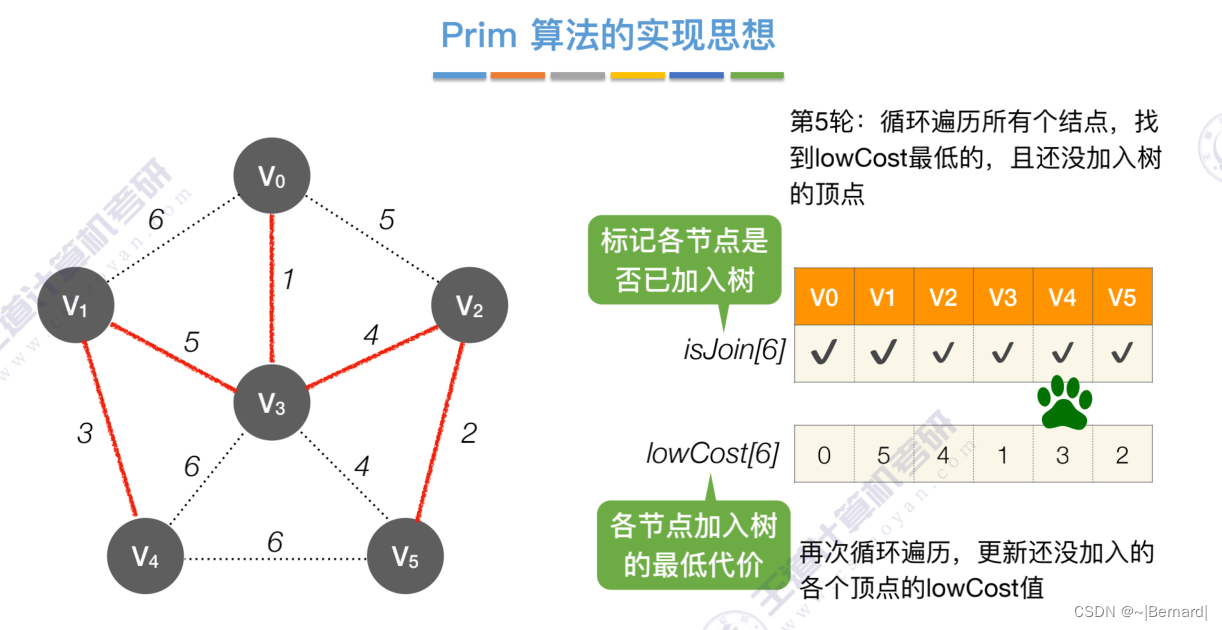
 如果一个顶点此时还没有加入一颗树里，那么此时可以检查一下这个顶点和新加入的顶点有没有边，如果他们之间有边，如果他们之间有边，并且这个值比以前的lowCast值更低的话，那么我们就需要去更新lowCast值。

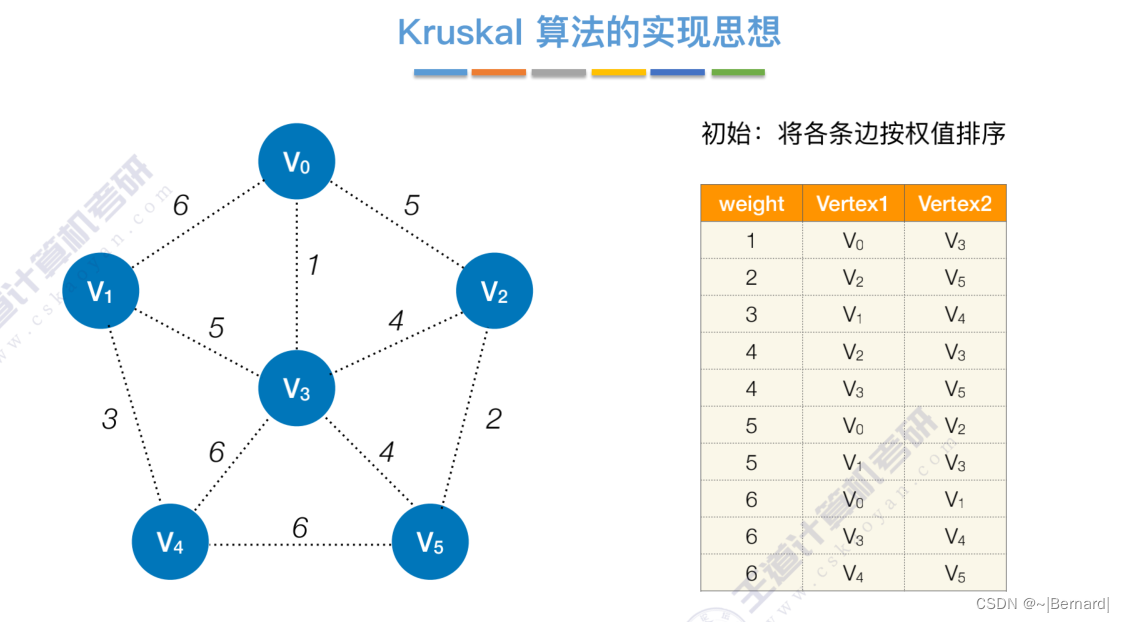
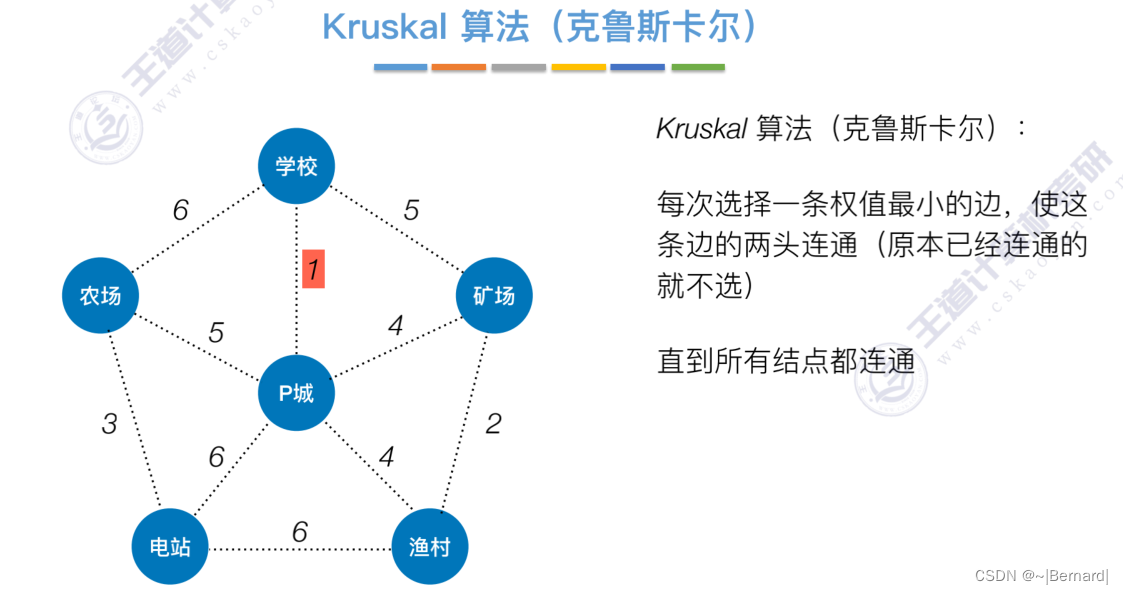
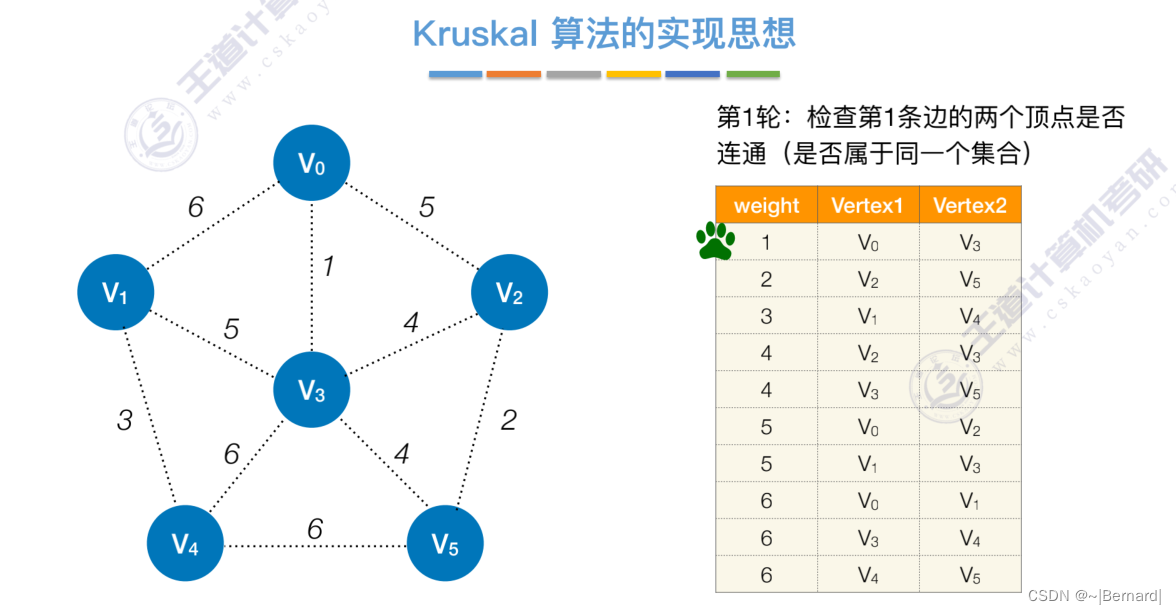
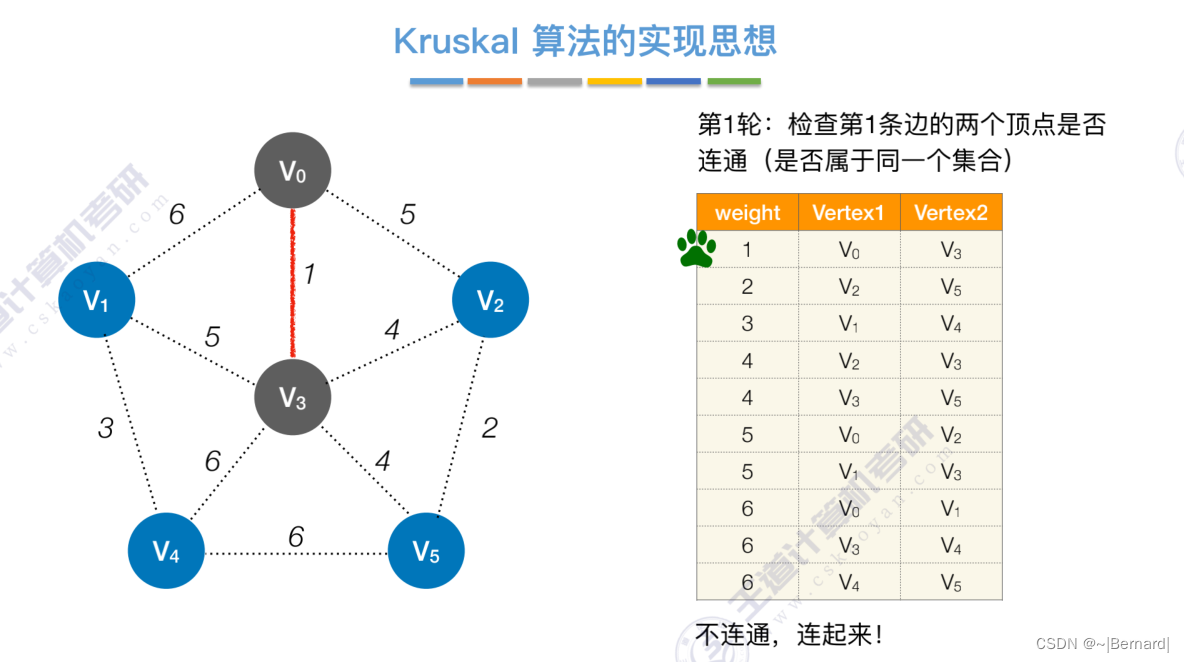
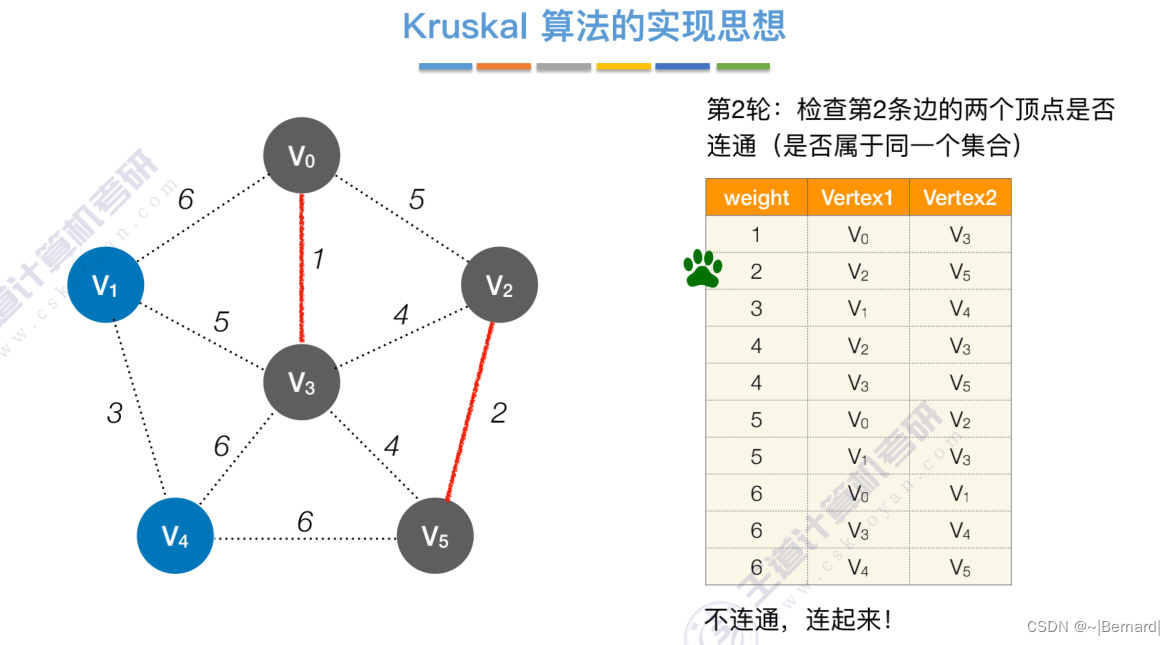
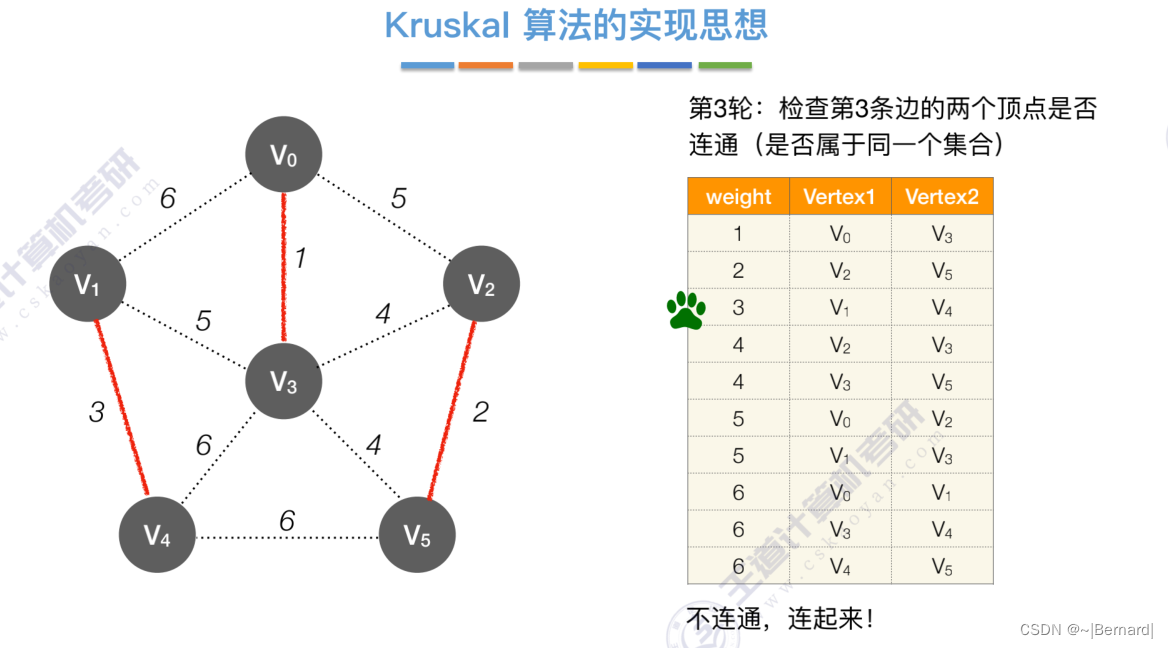
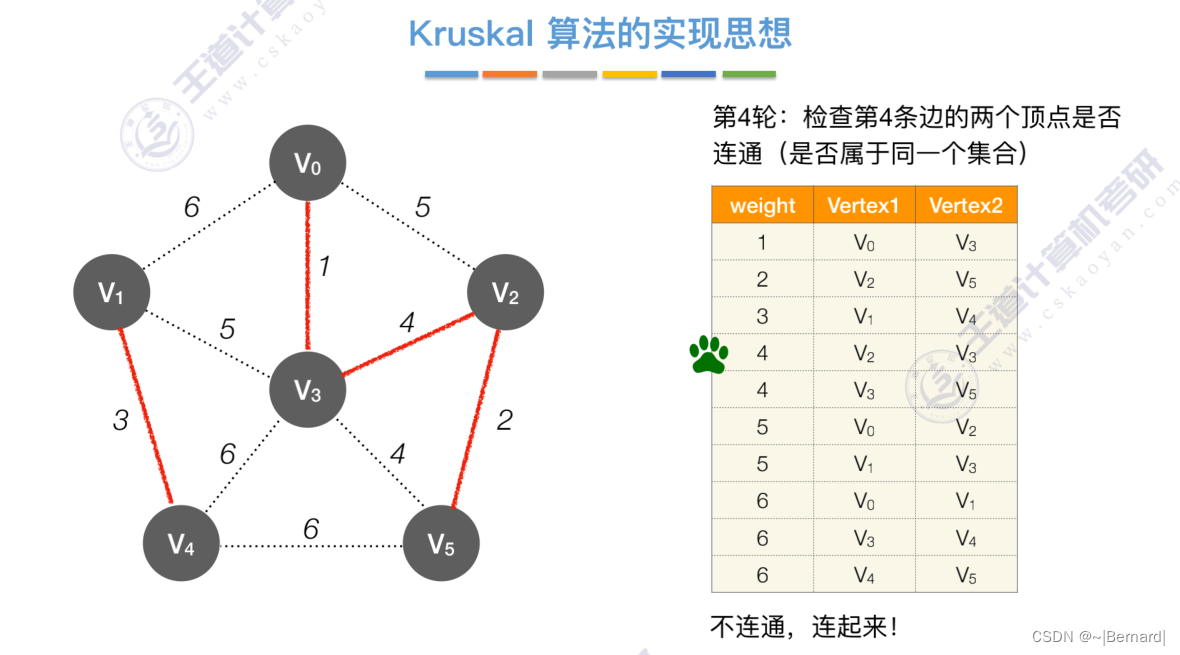
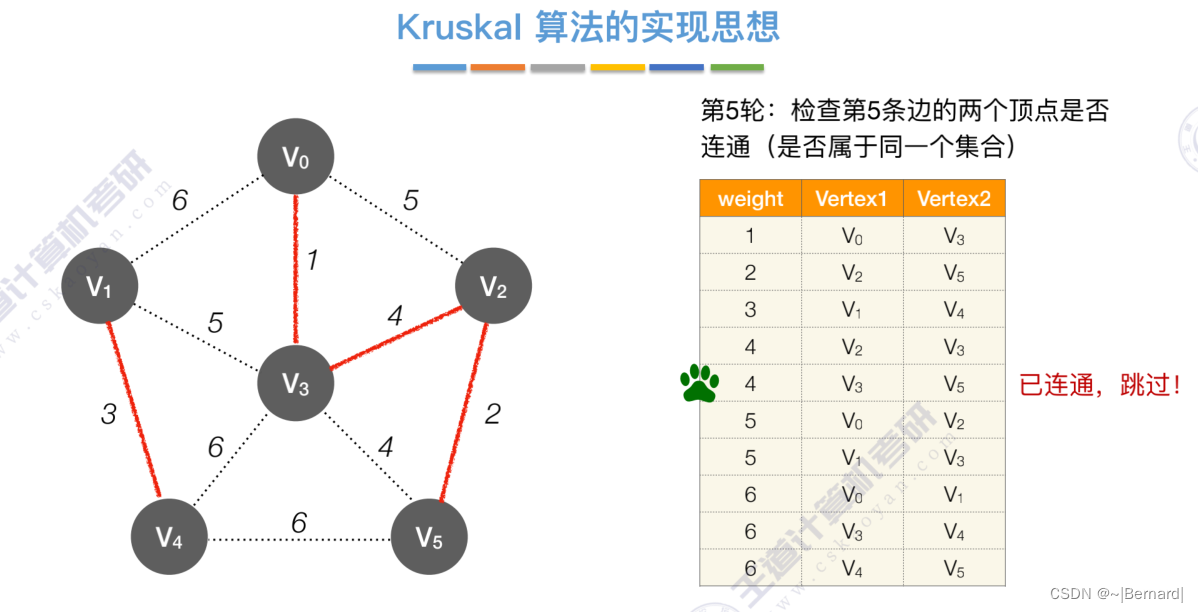
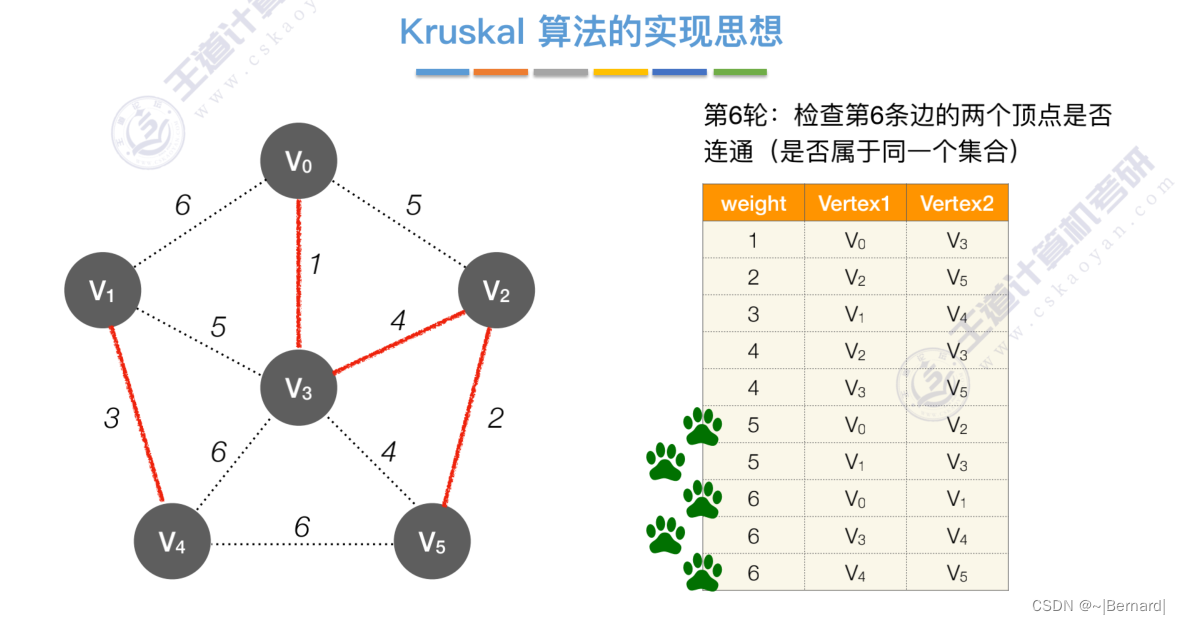
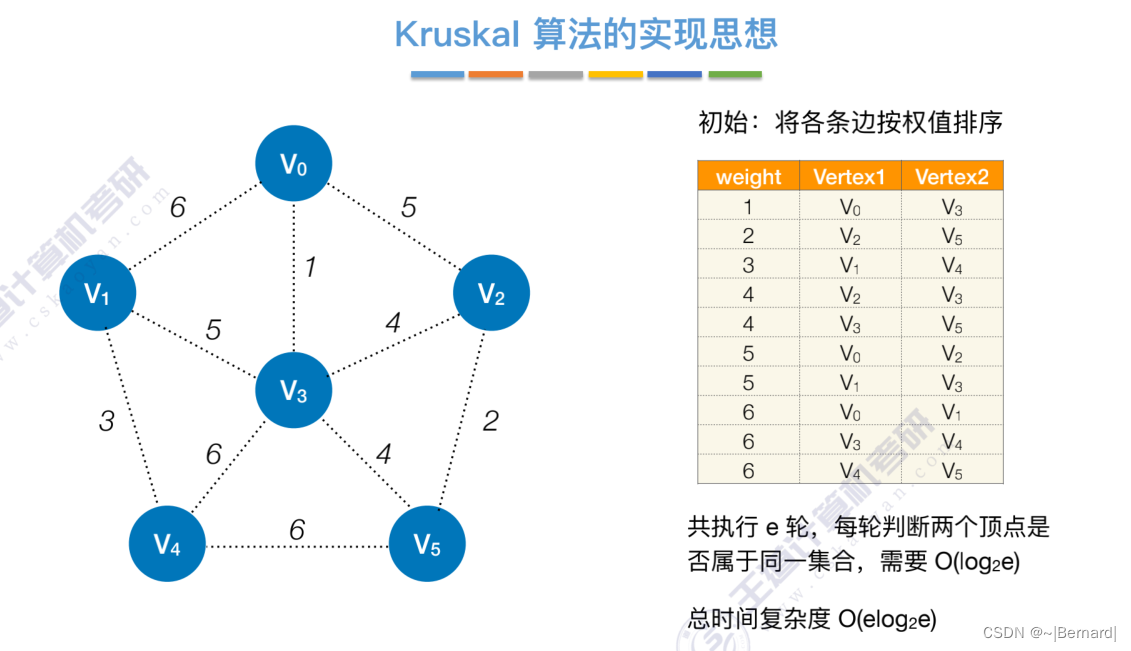
 Kruskal算法中运用到了并查集的思想，判断两个顶点是否在同一个集合中，没有在同一个集合则并起来，同属于一个集合说明已经连通，则跳过

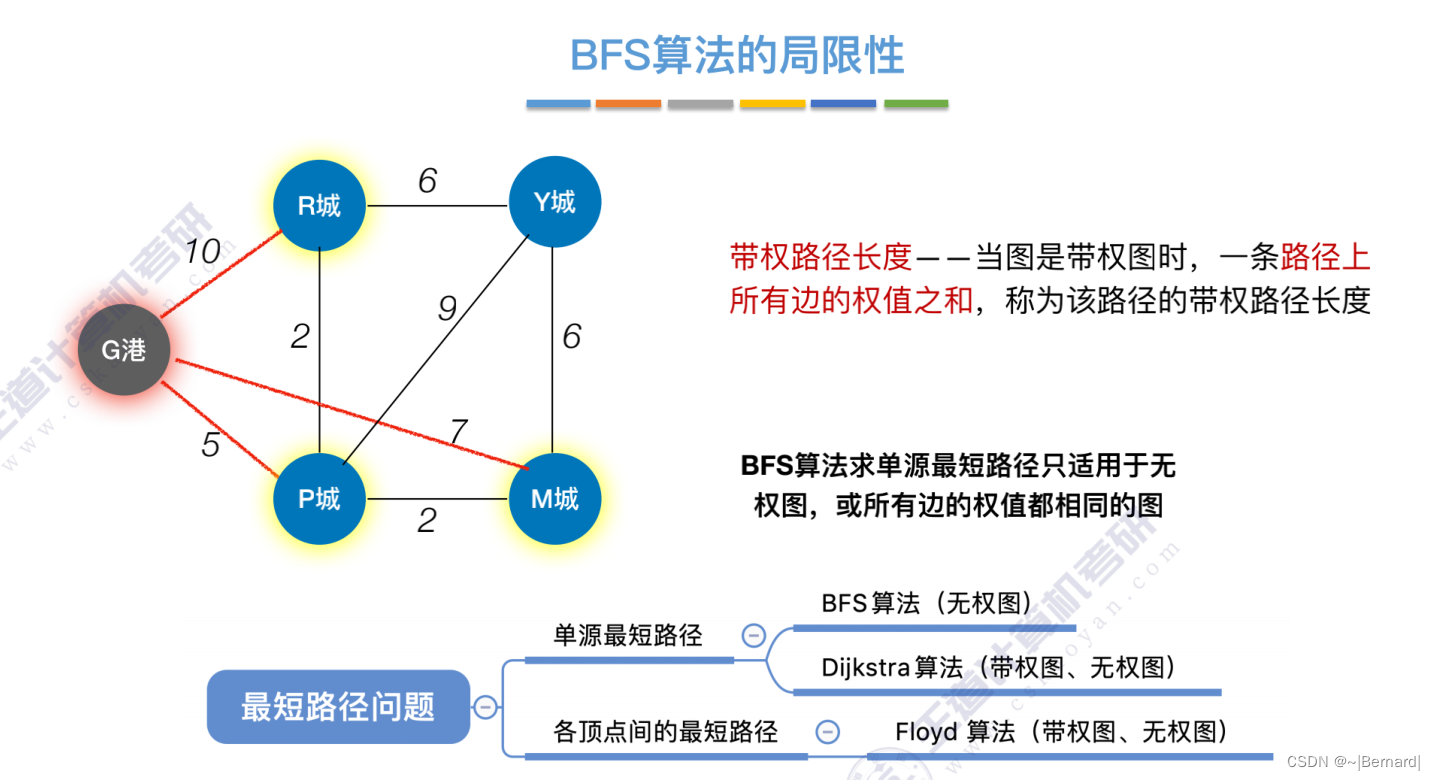
 6.4.2 最短路径问题

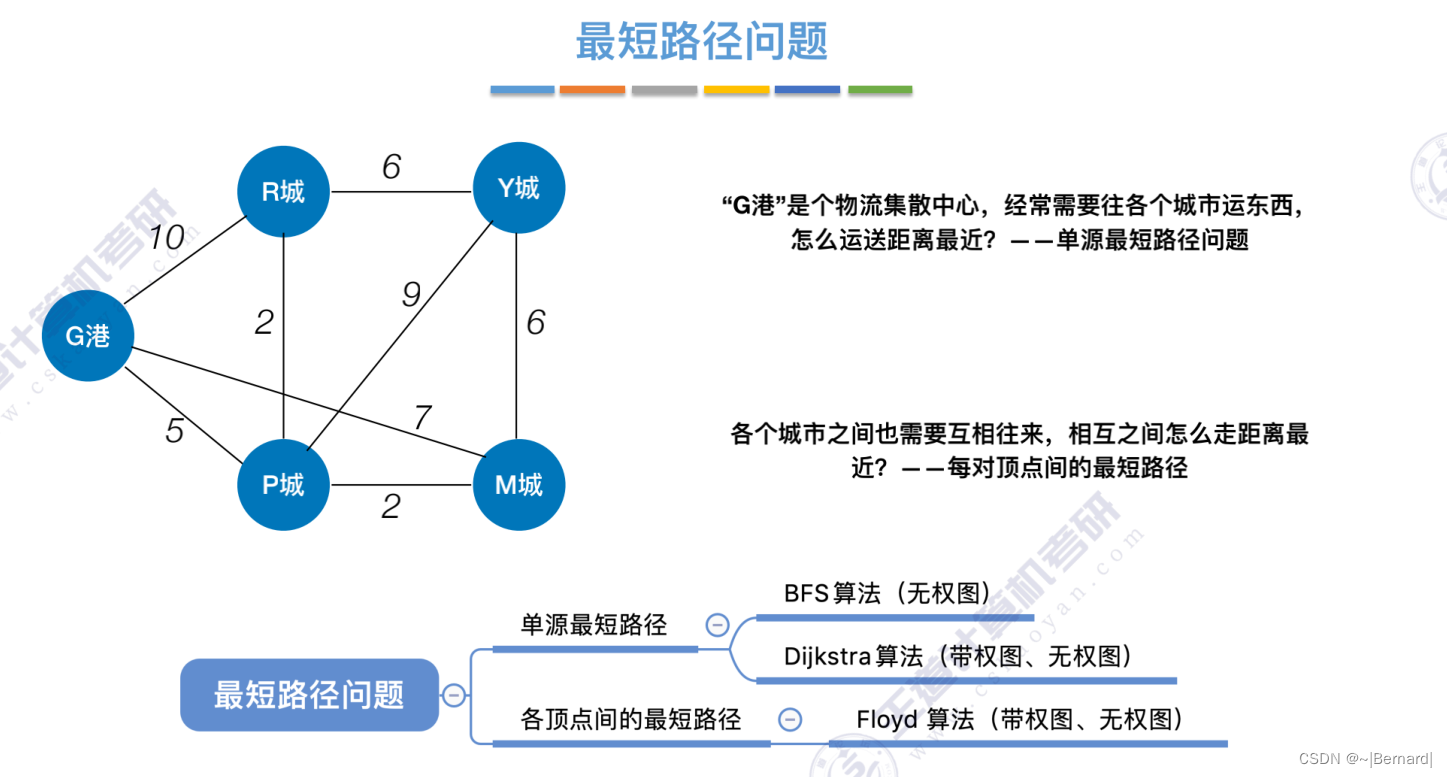
 单源--只有一个源头，最短路径--从这个节点到达其他任意节点的最短路径。

 

 

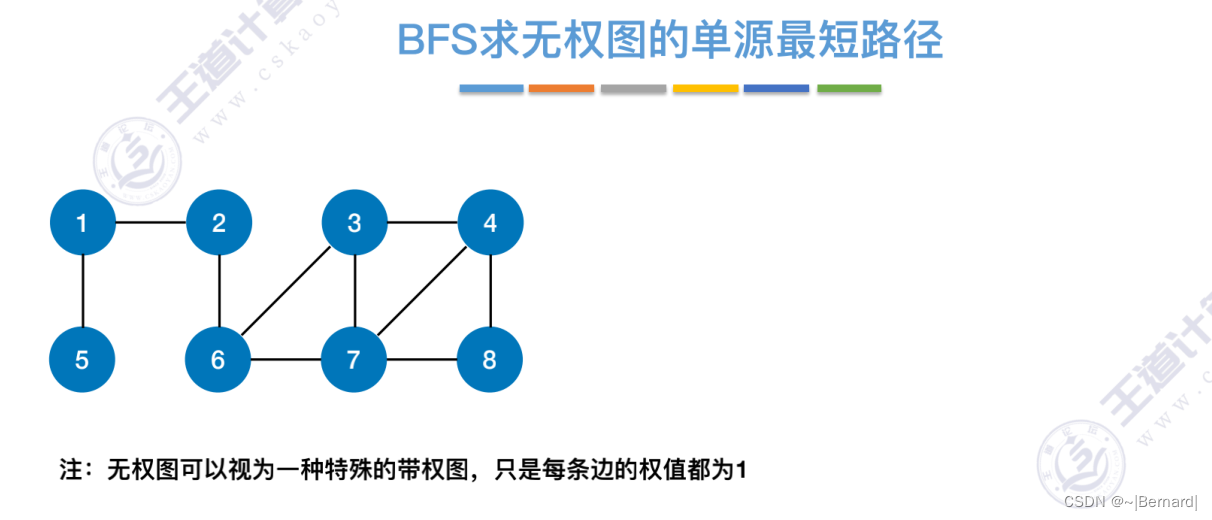
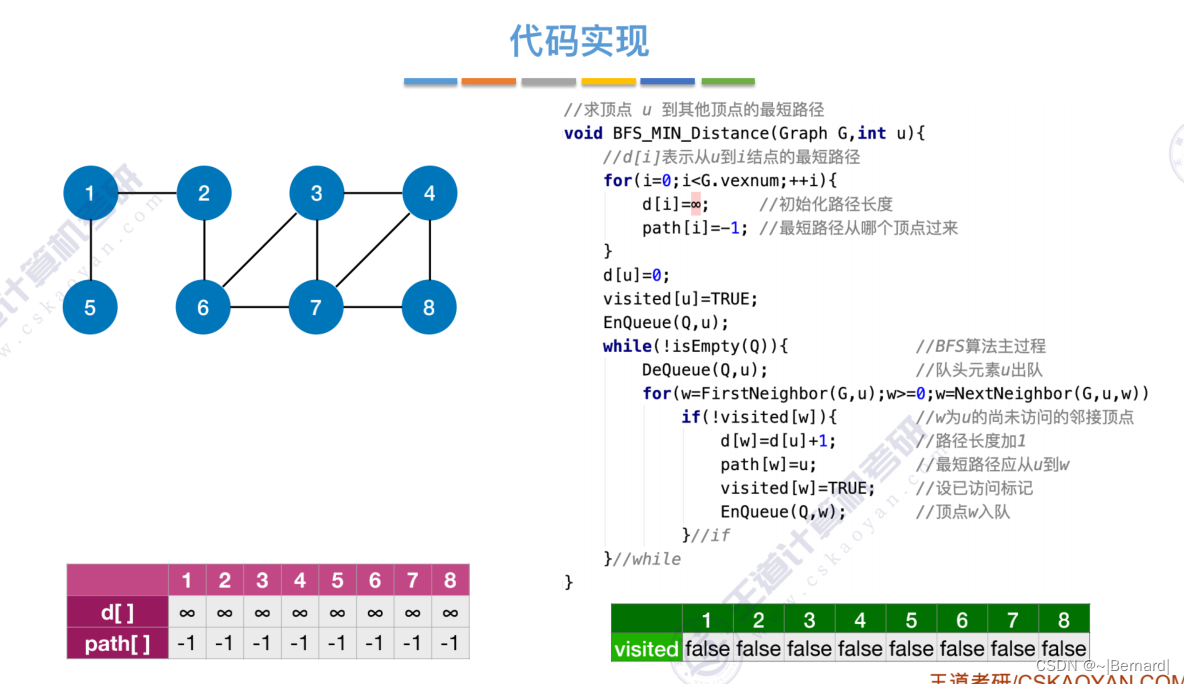
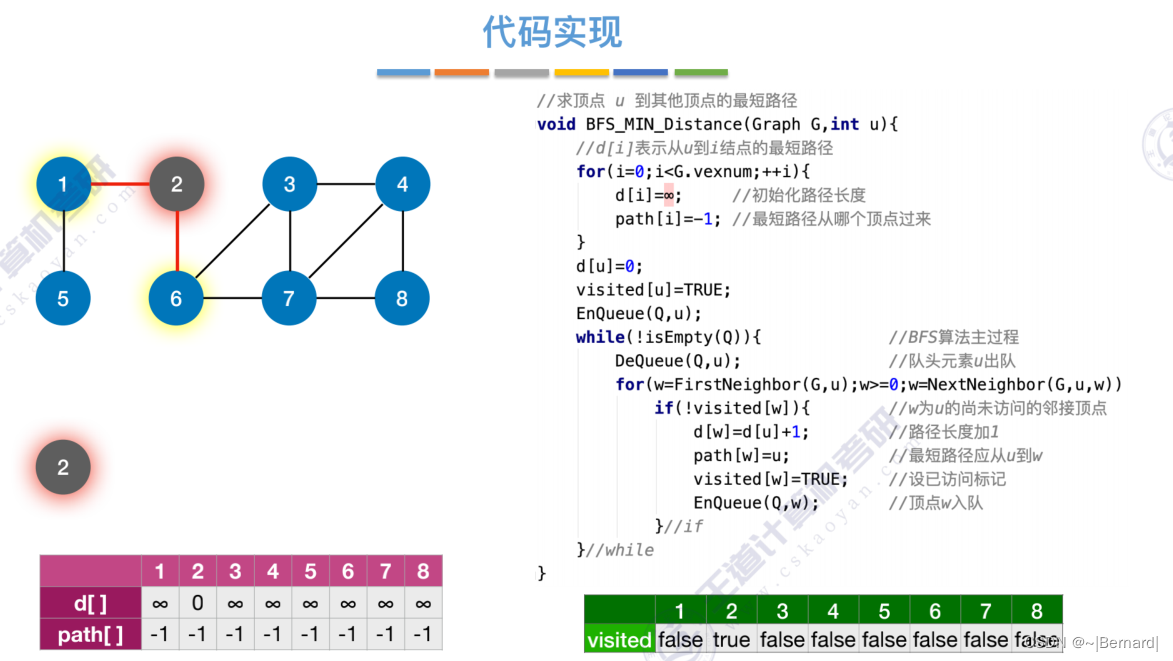
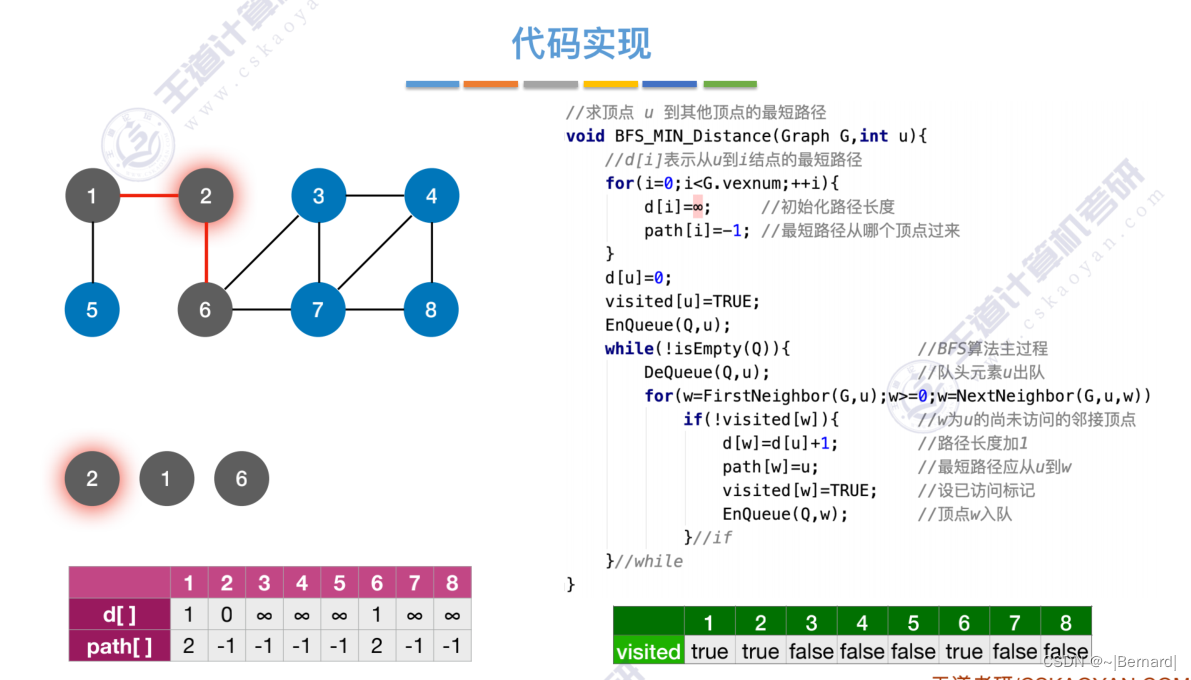
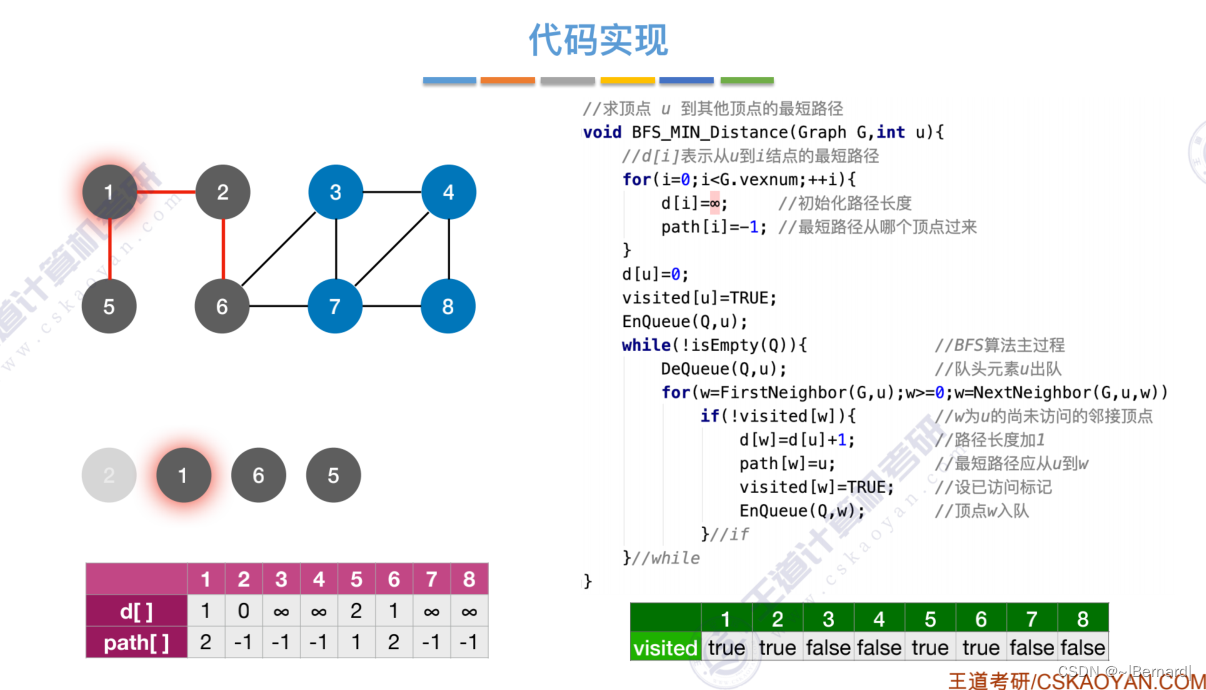
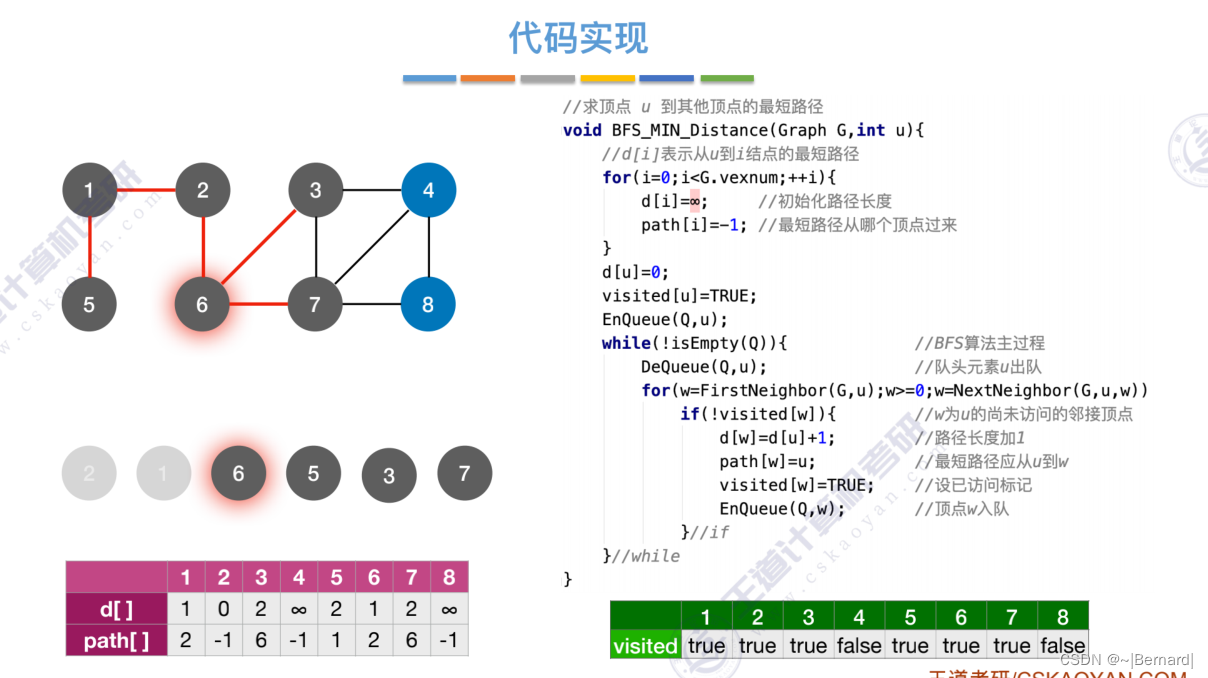
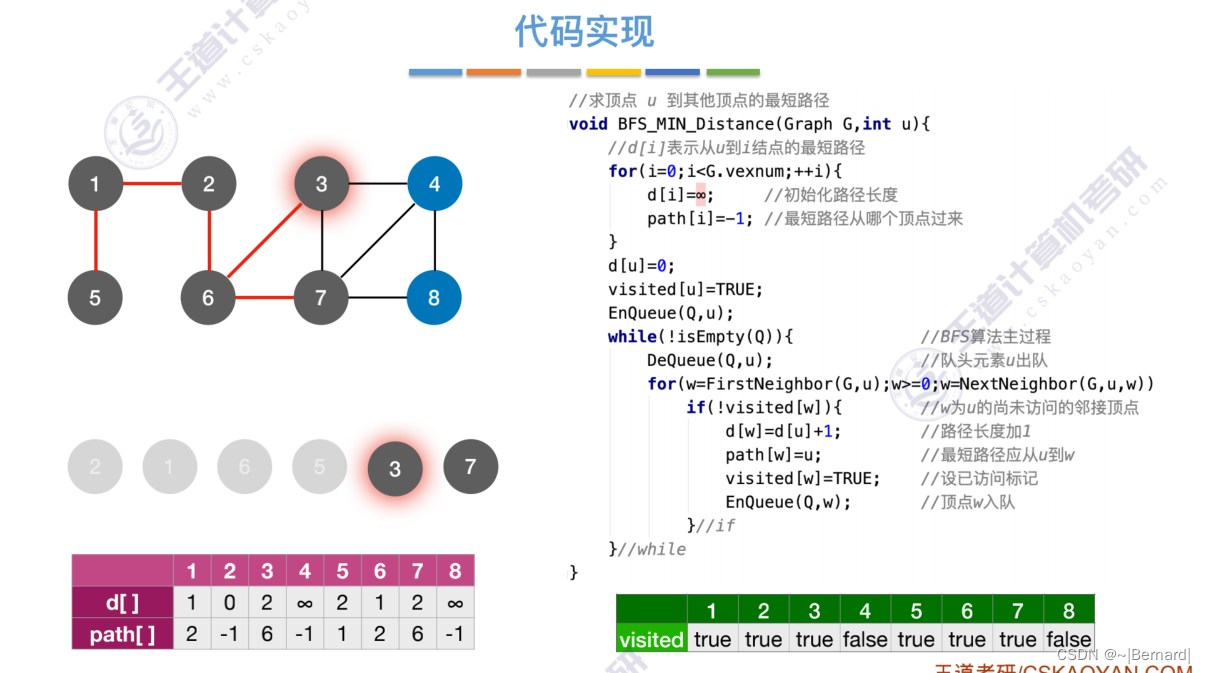
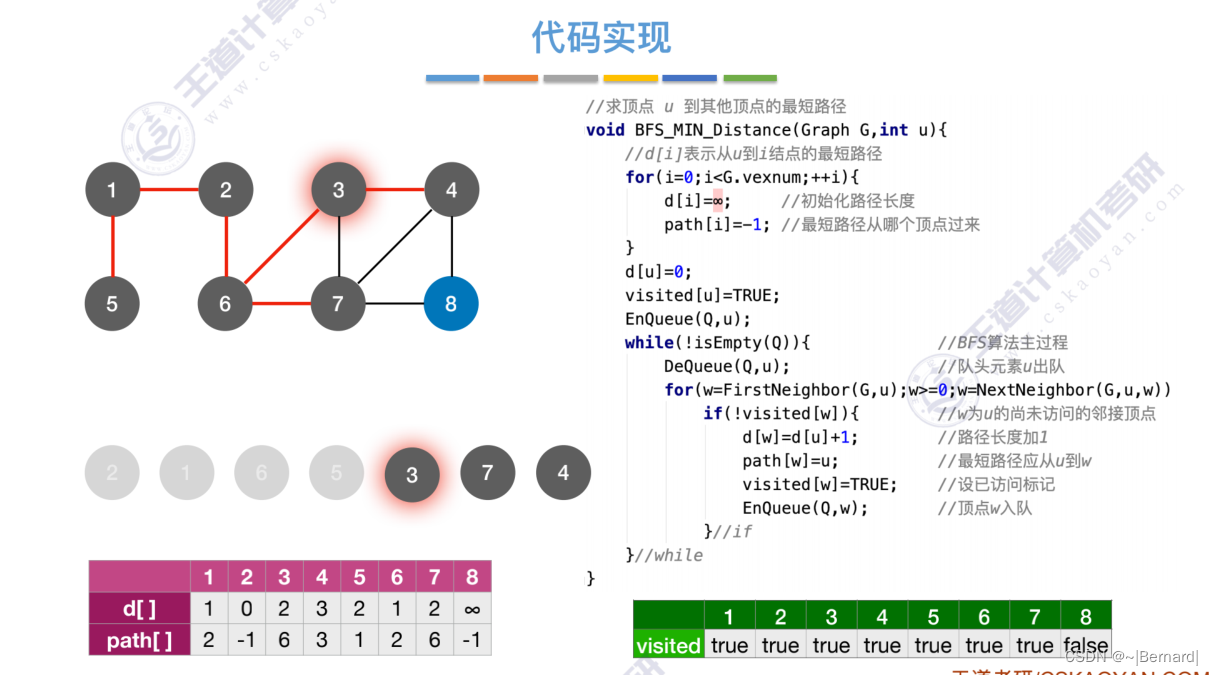
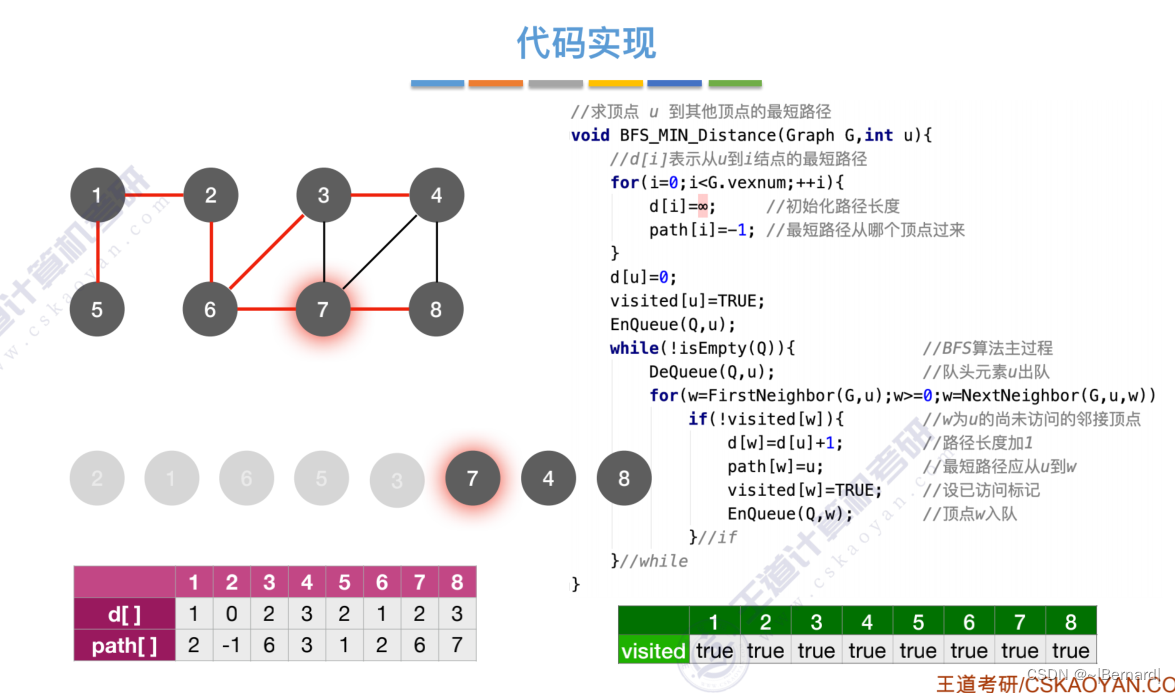
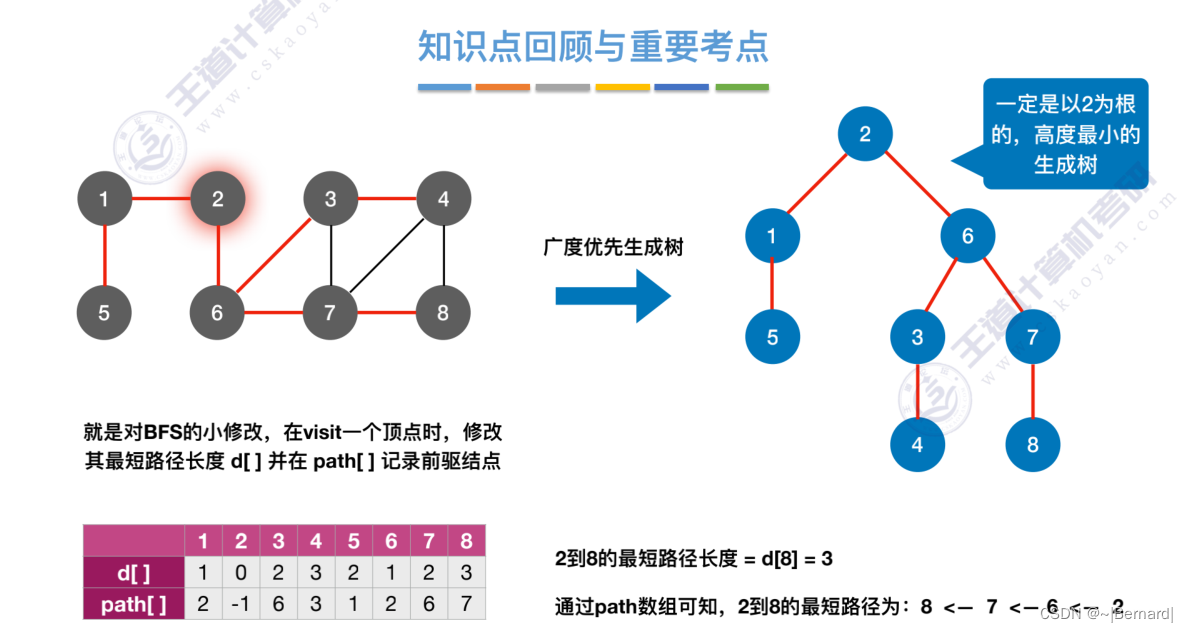
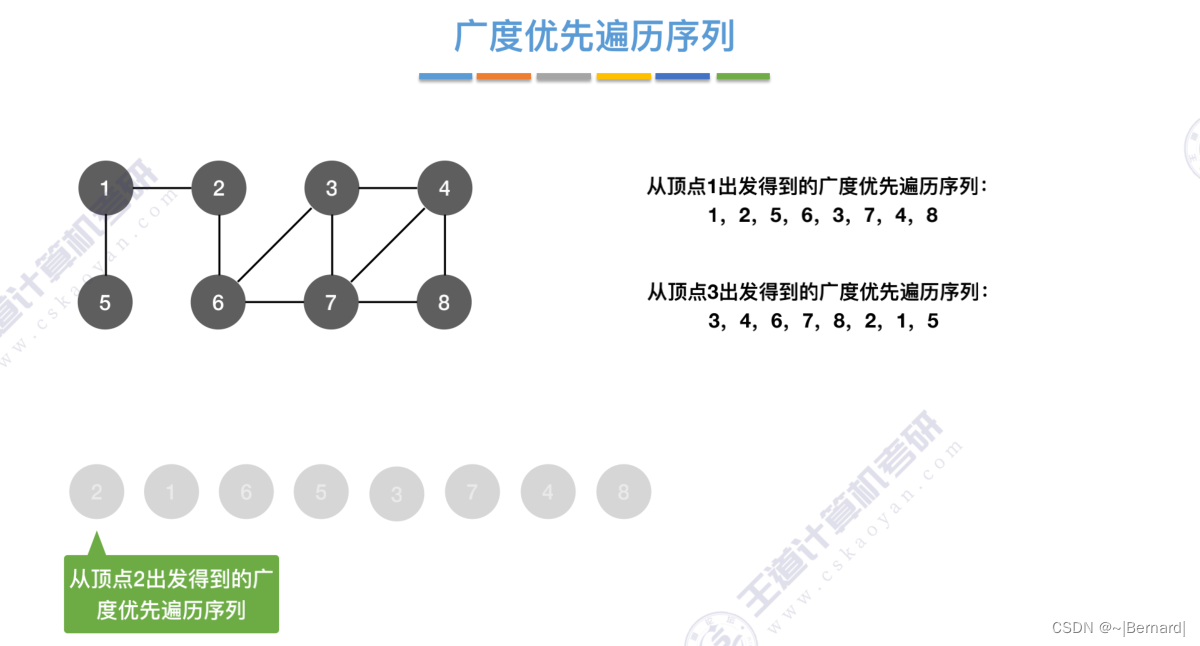
每一个节点在第几层也直接反映了从起点2达到这些节点的距离是多少。

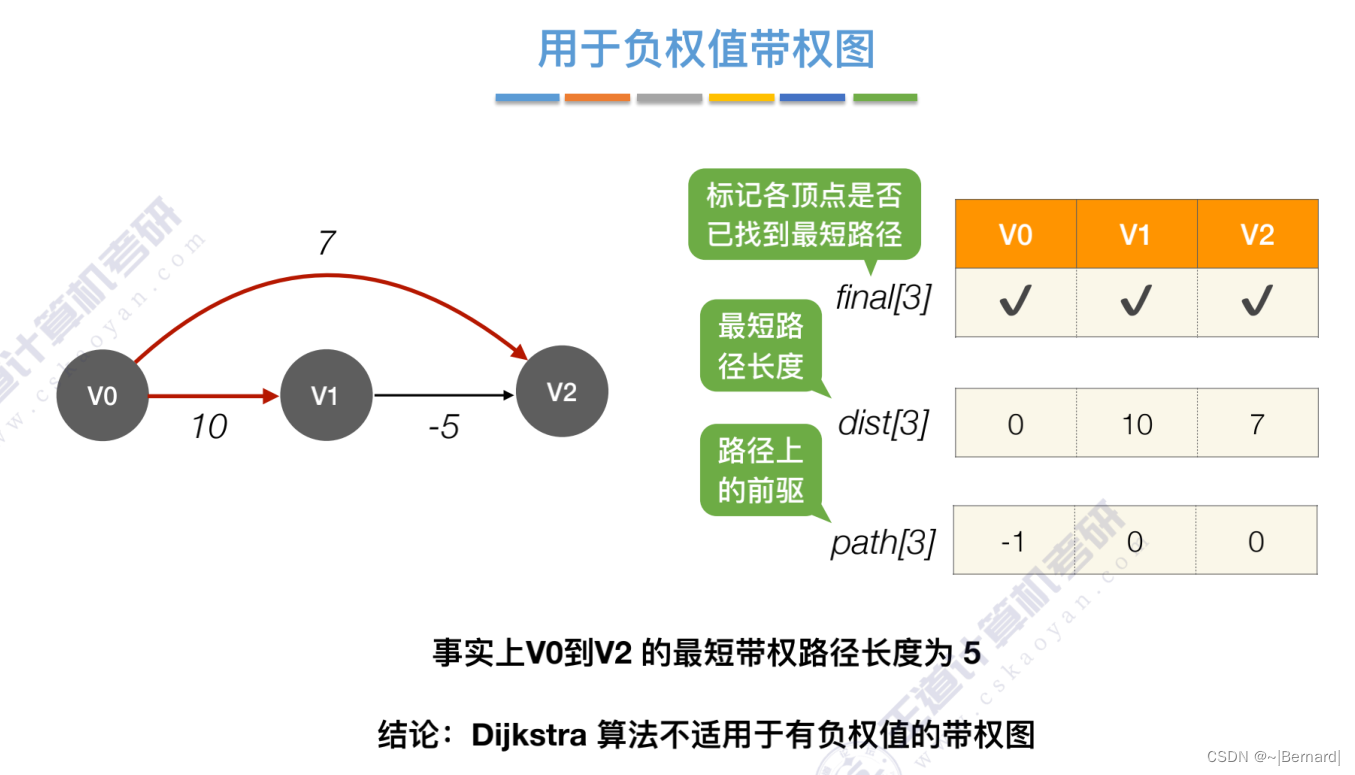
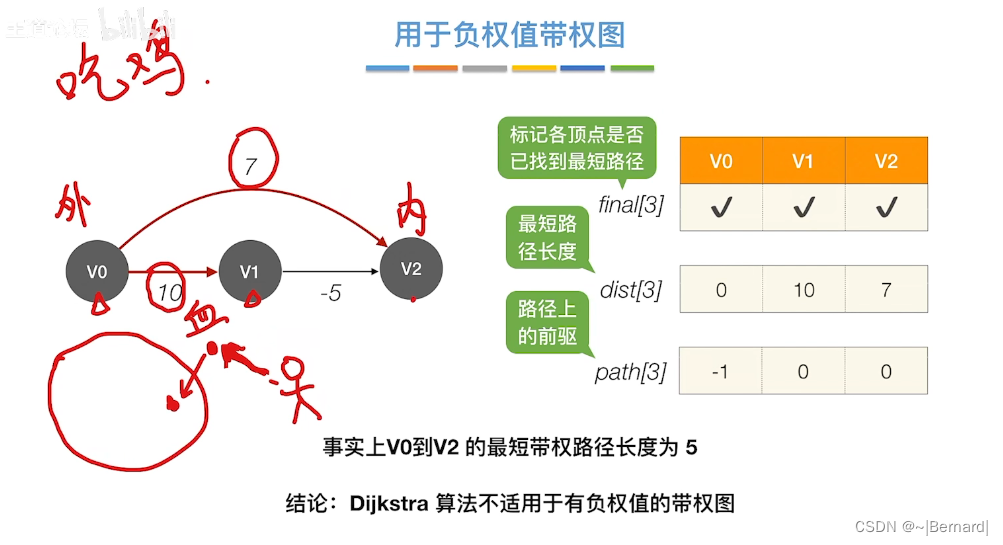
6.4.3 最短路径问题(Dijkstra算法)

 

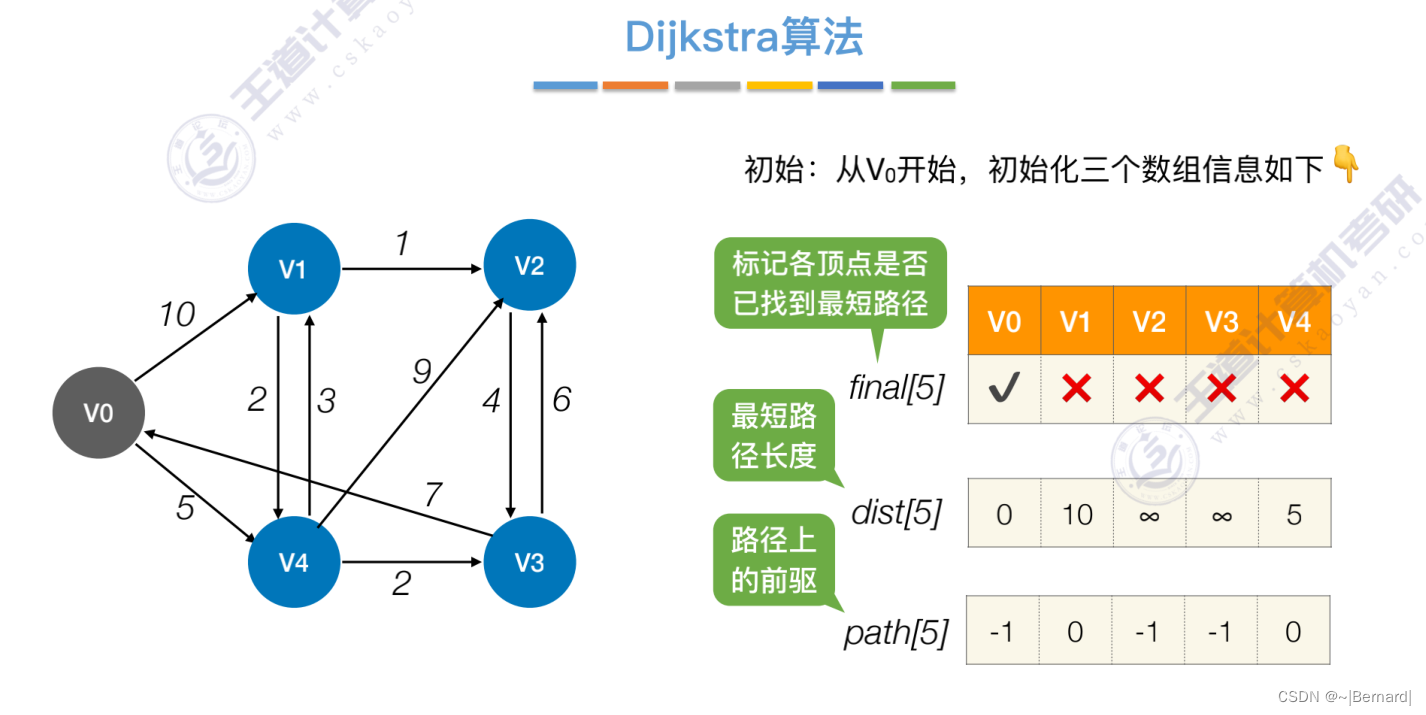
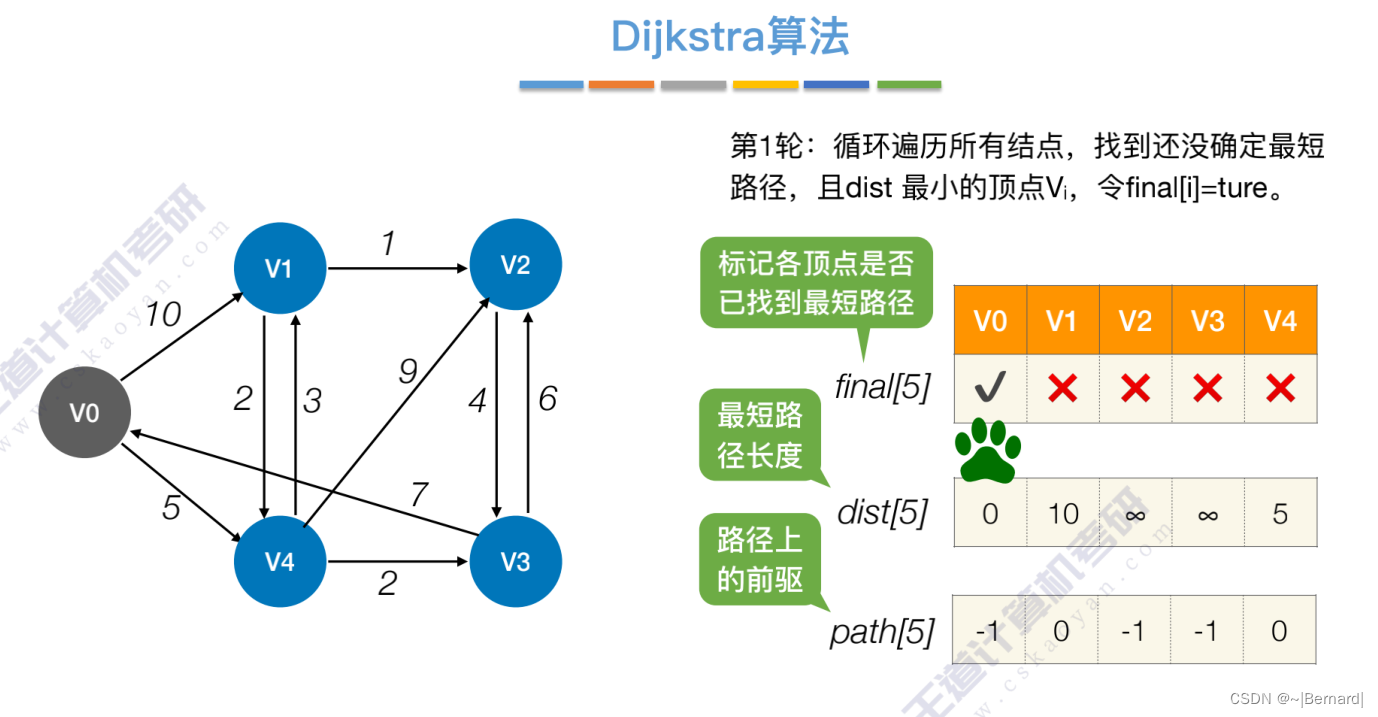
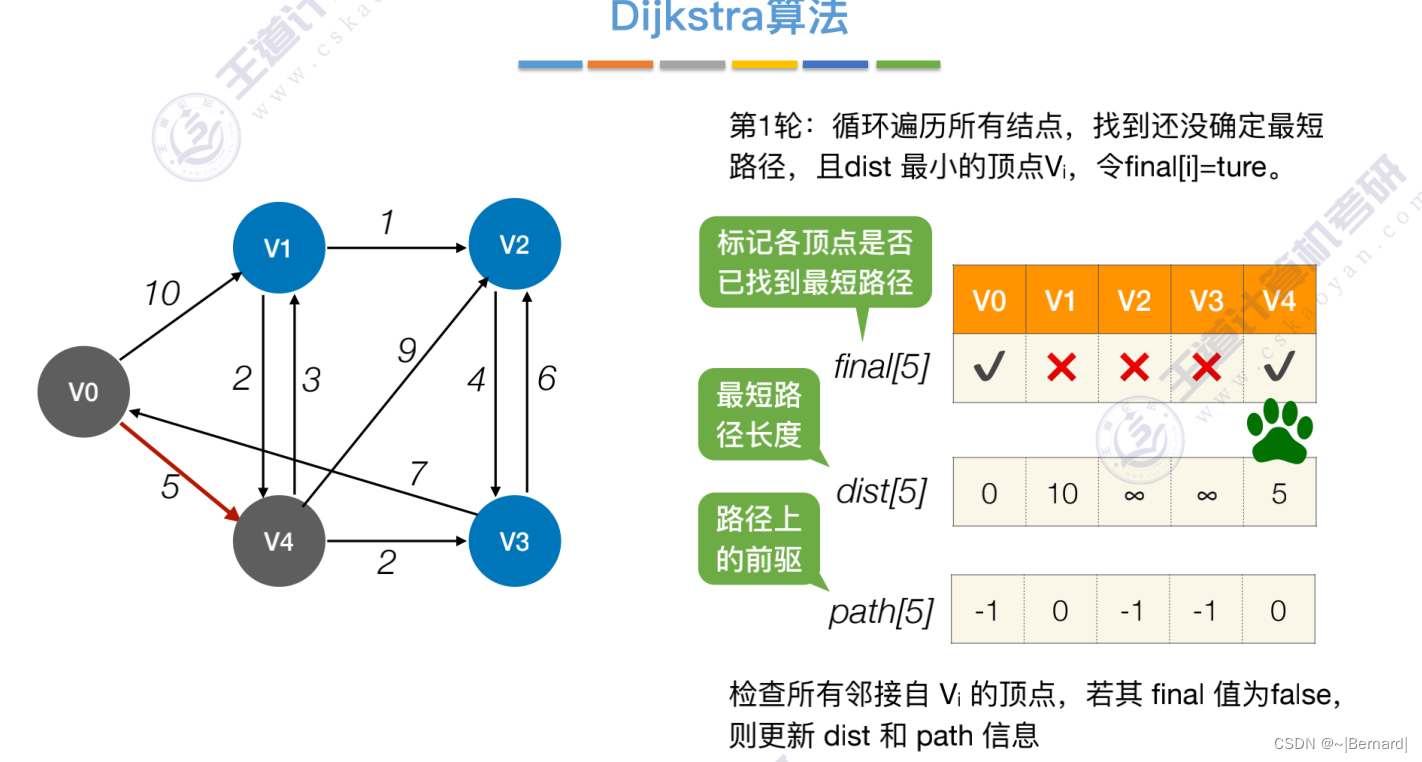
 注：检查所有邻接自Vi(能从Vi直接到达)的顶点

 

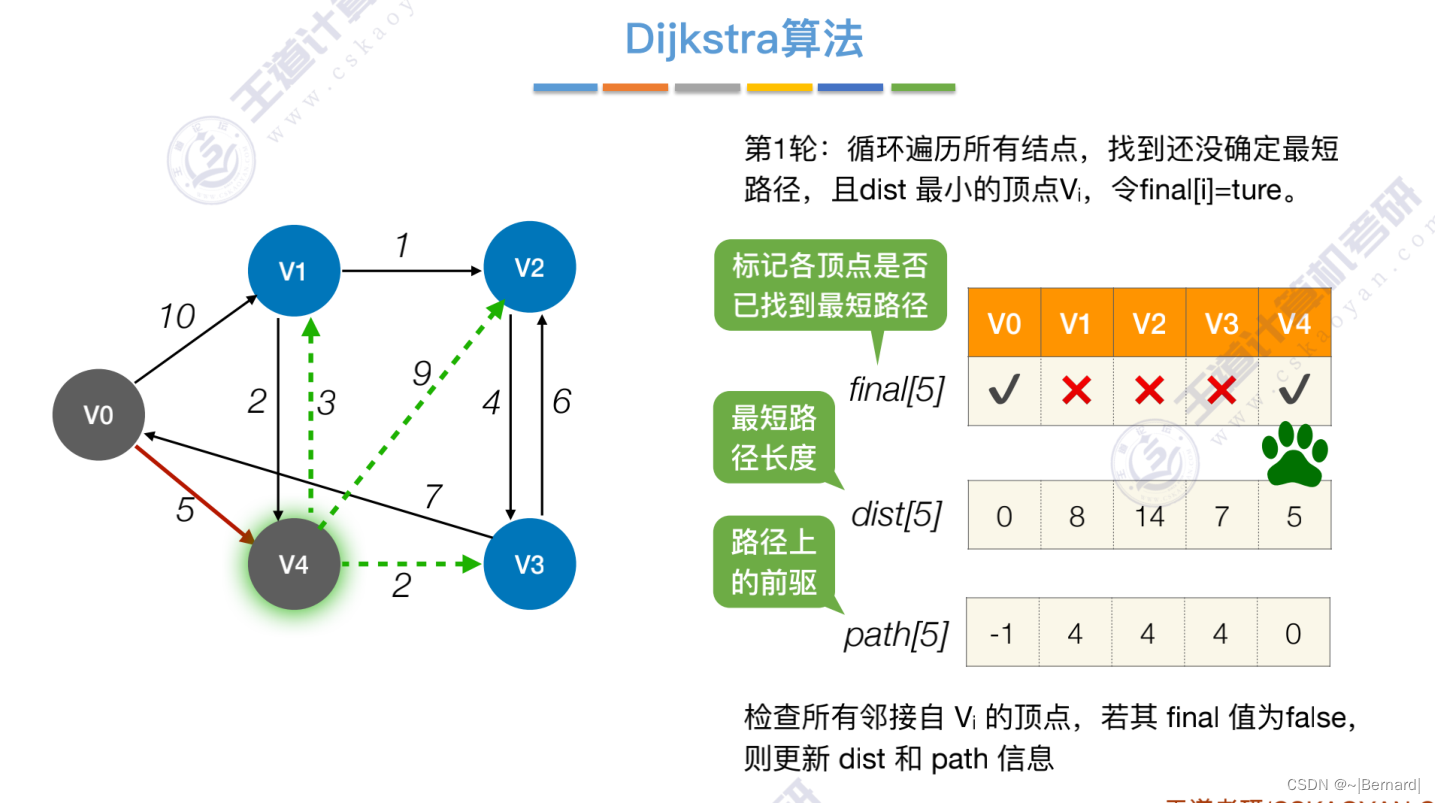
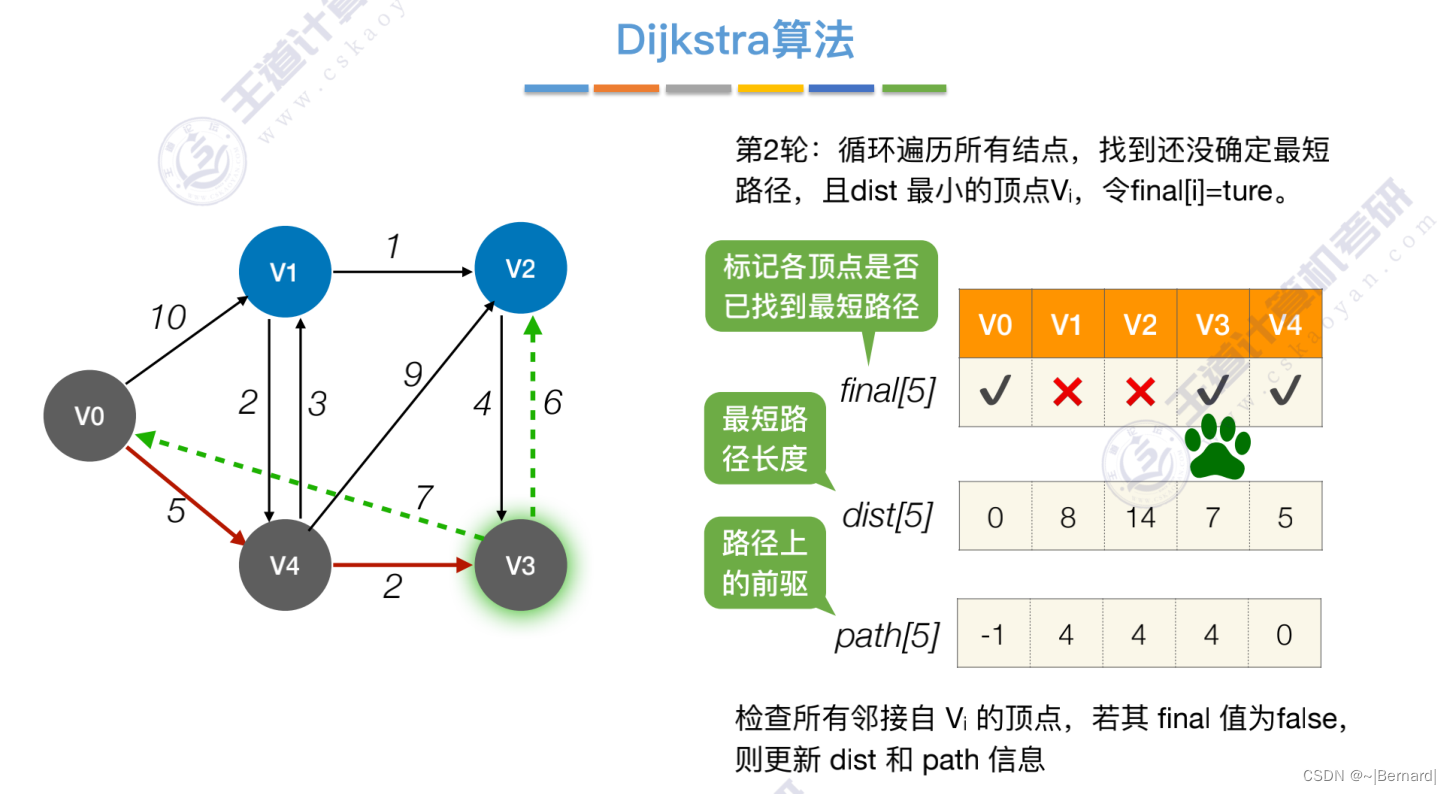
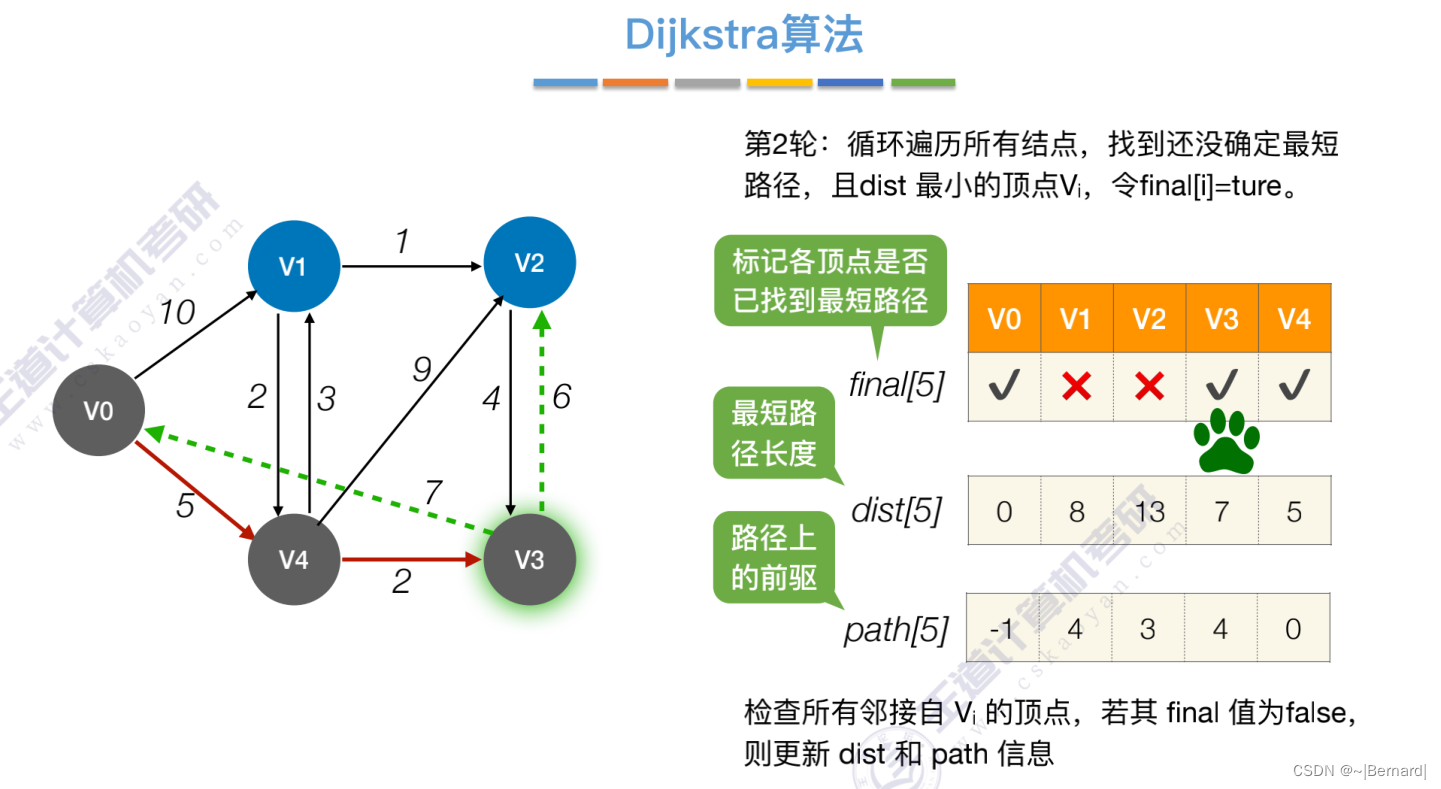
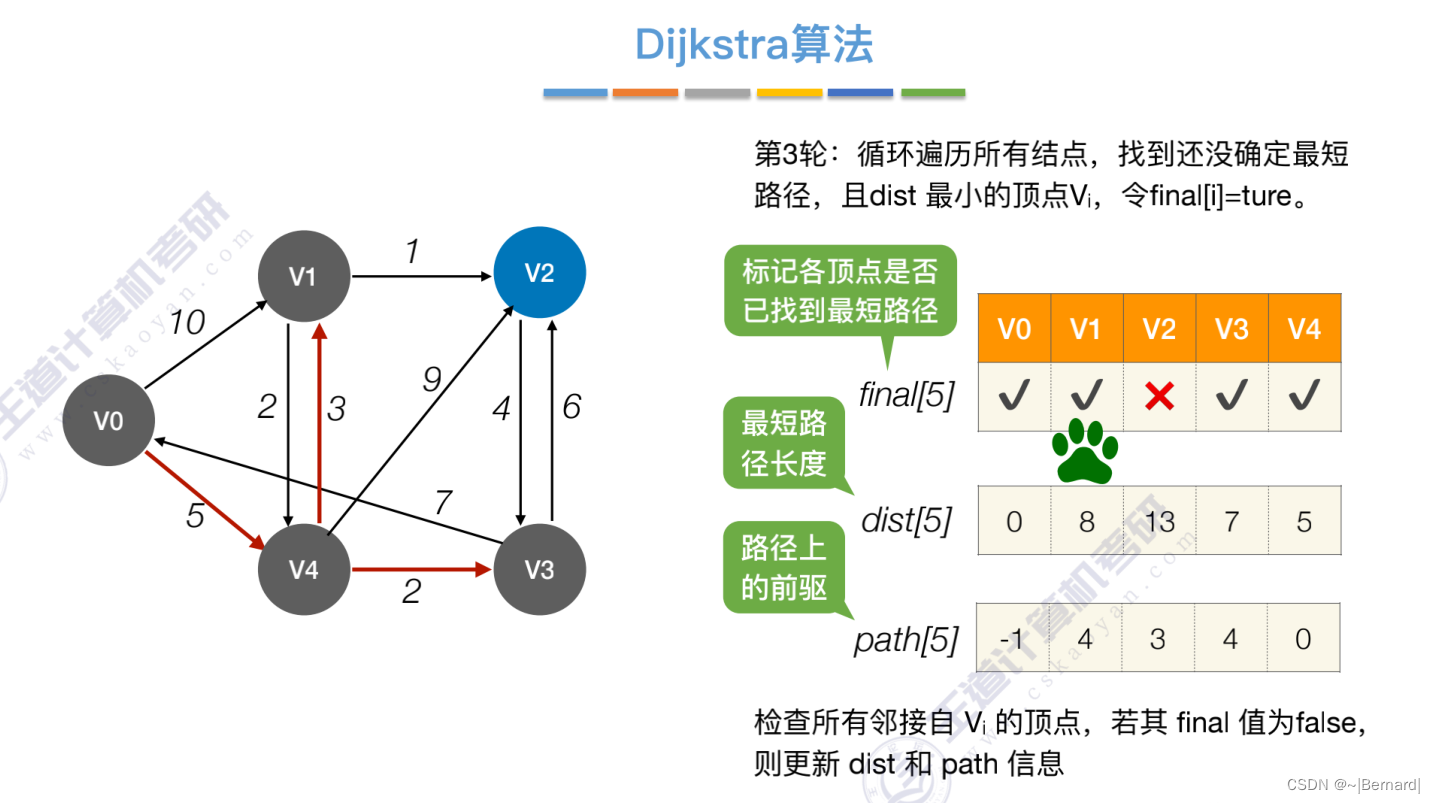
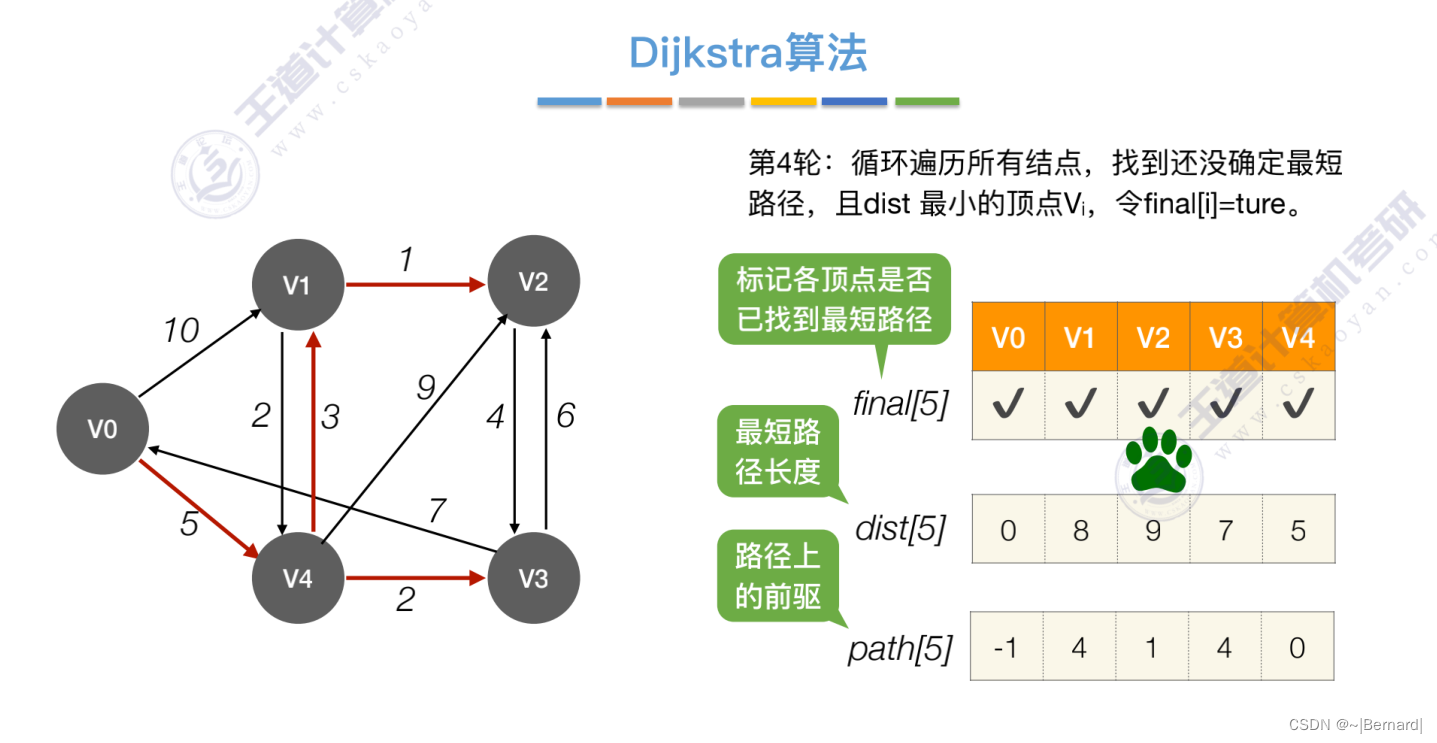
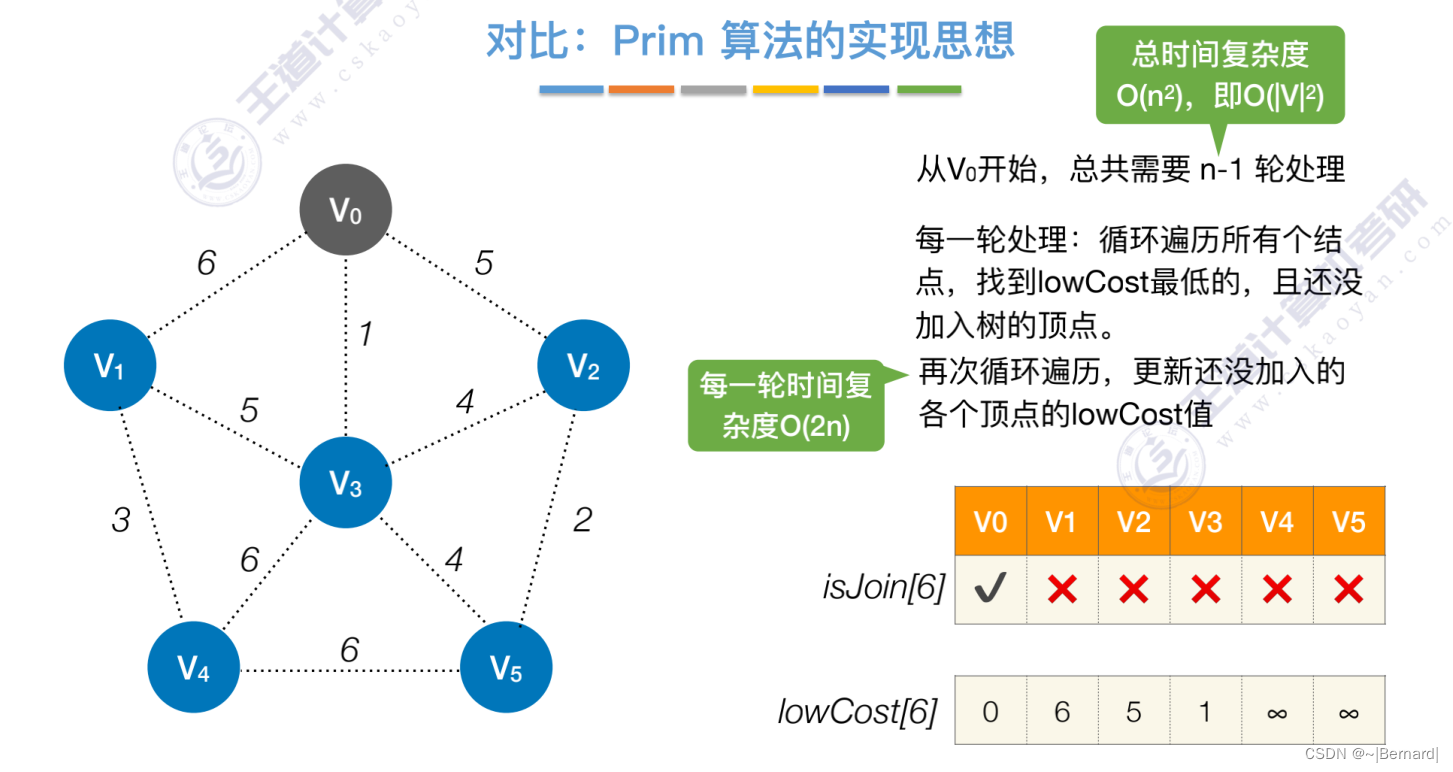
 Prim算法中的lowCast记录的是当前顶点加入到目前组建的最小生成树的最小代价。

而Dijikstra算法dist记录的是从从源头到指定顶点的最短路径的值。

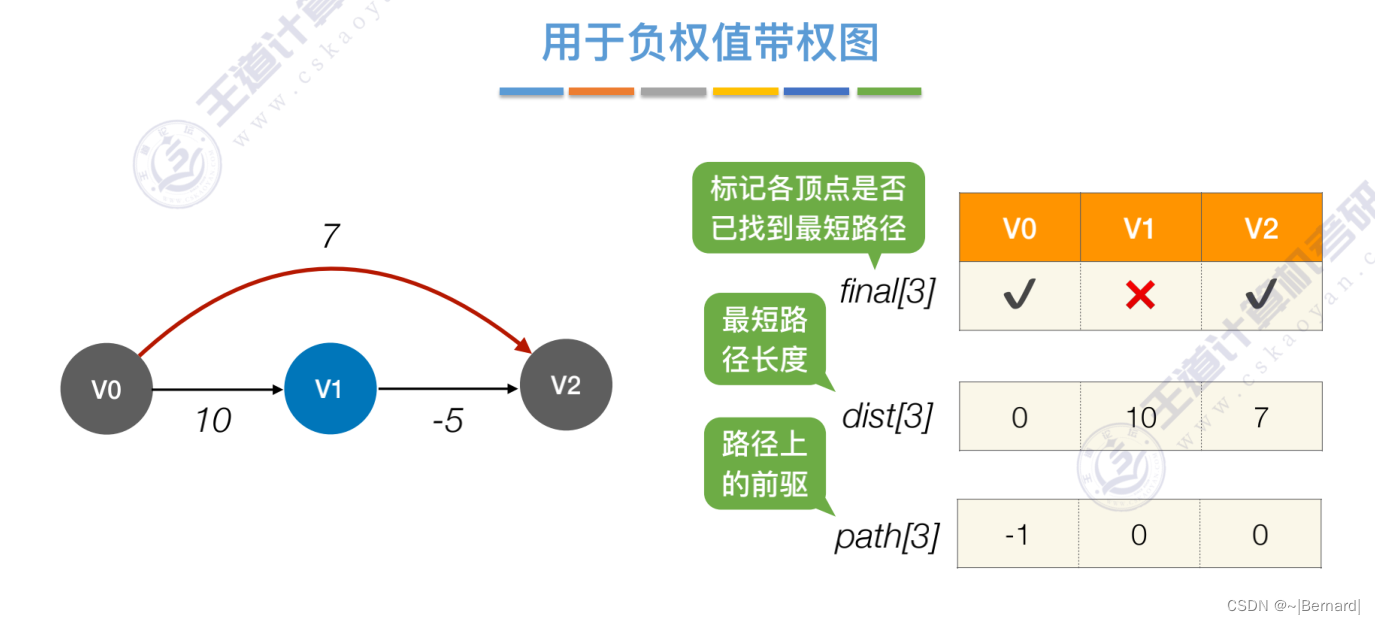
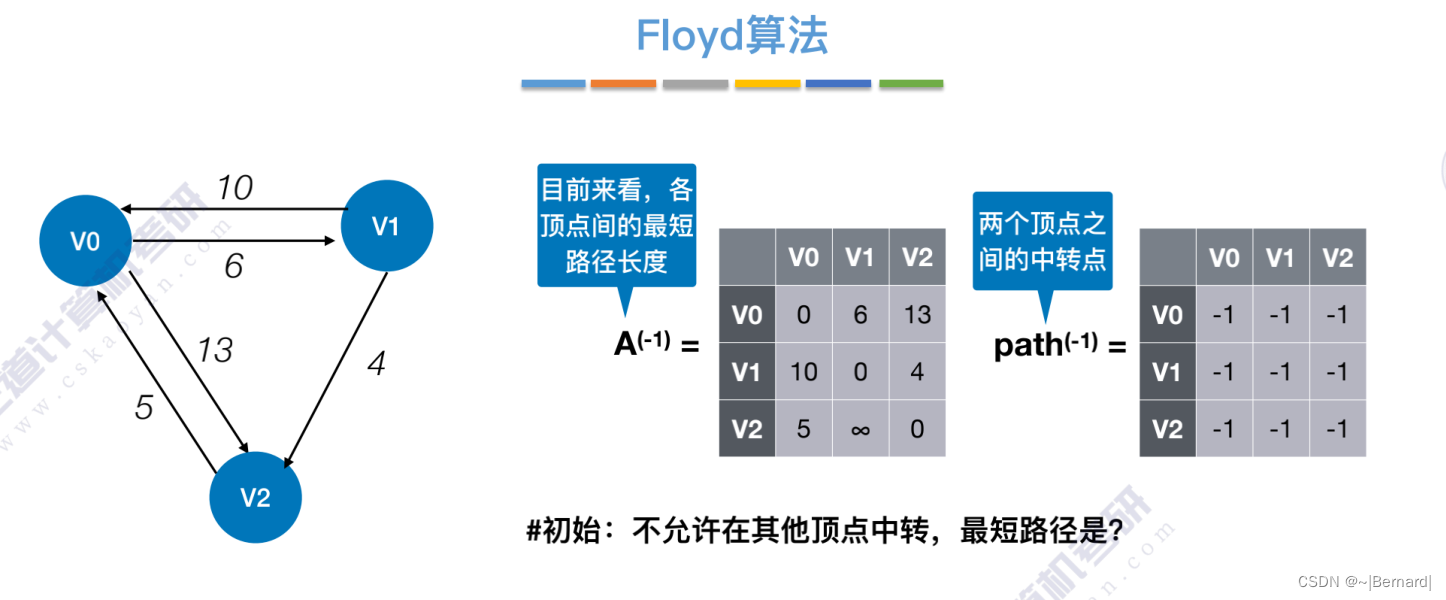
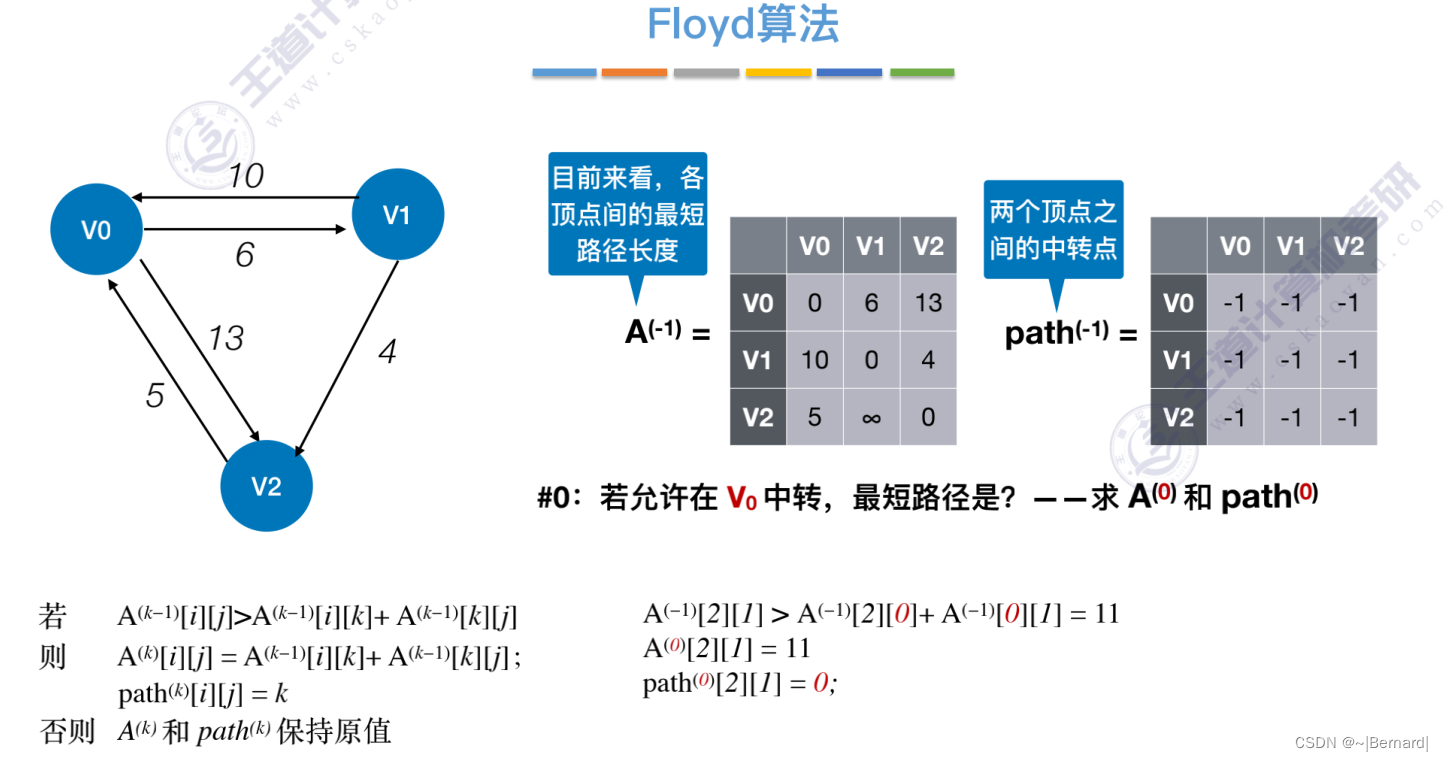
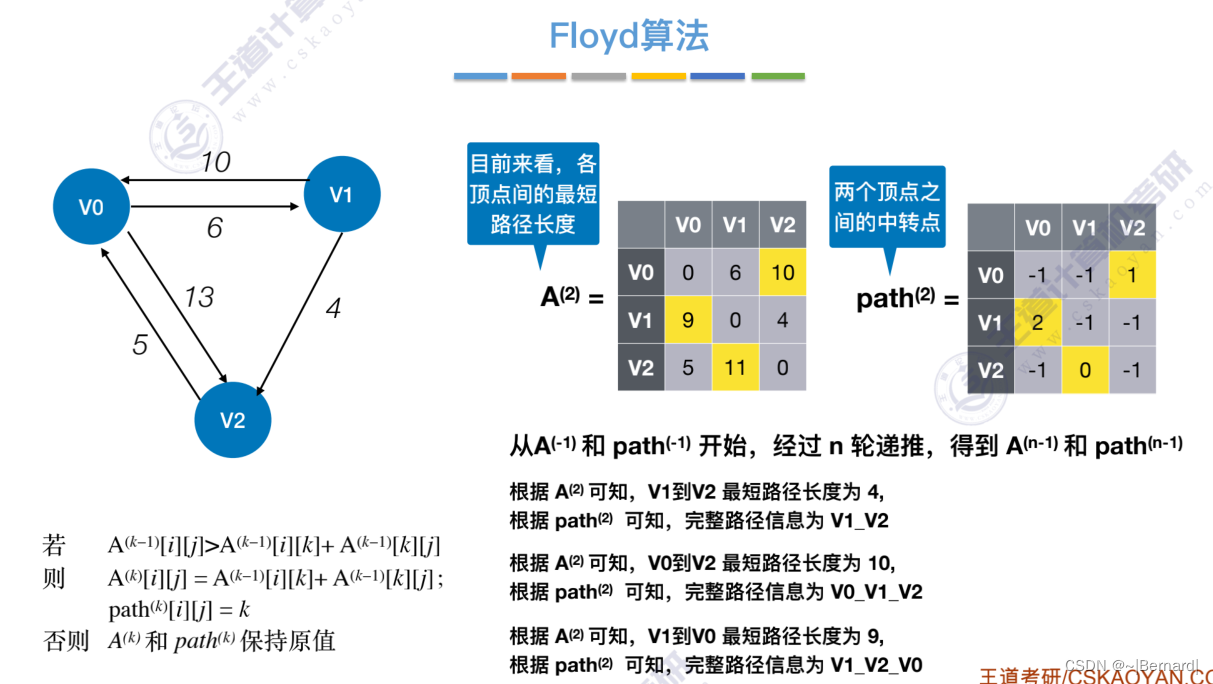
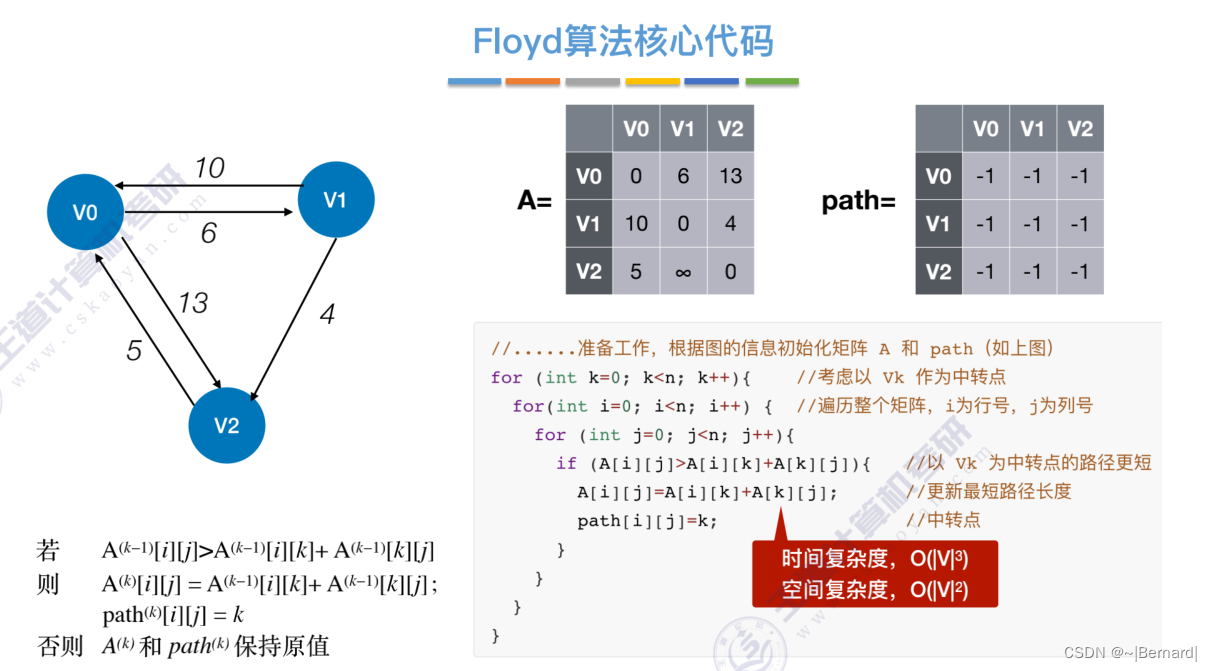
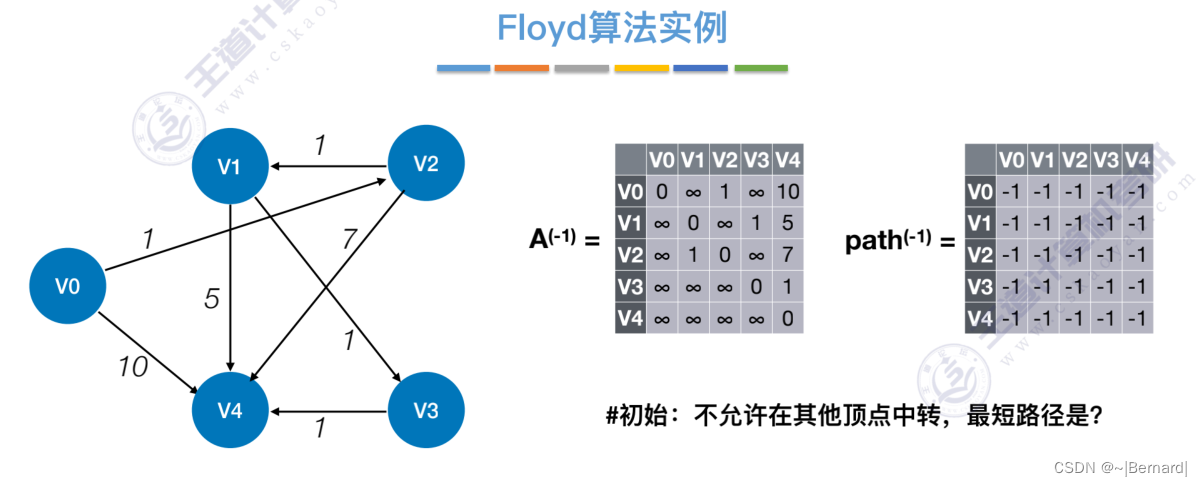
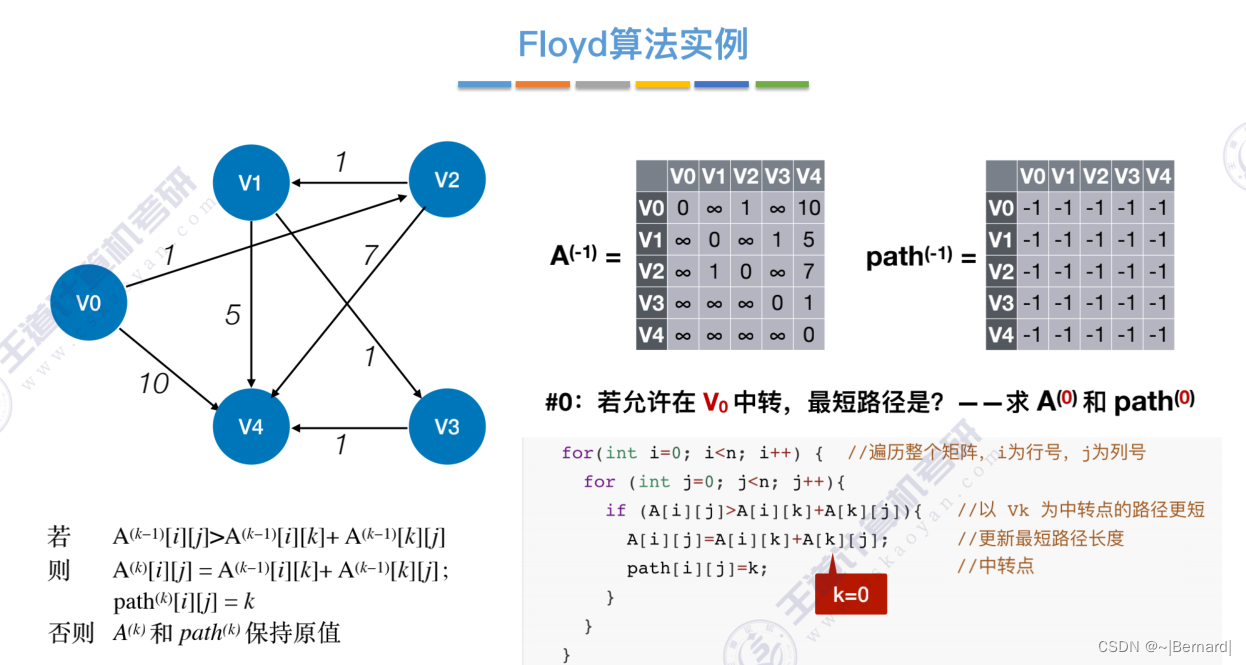
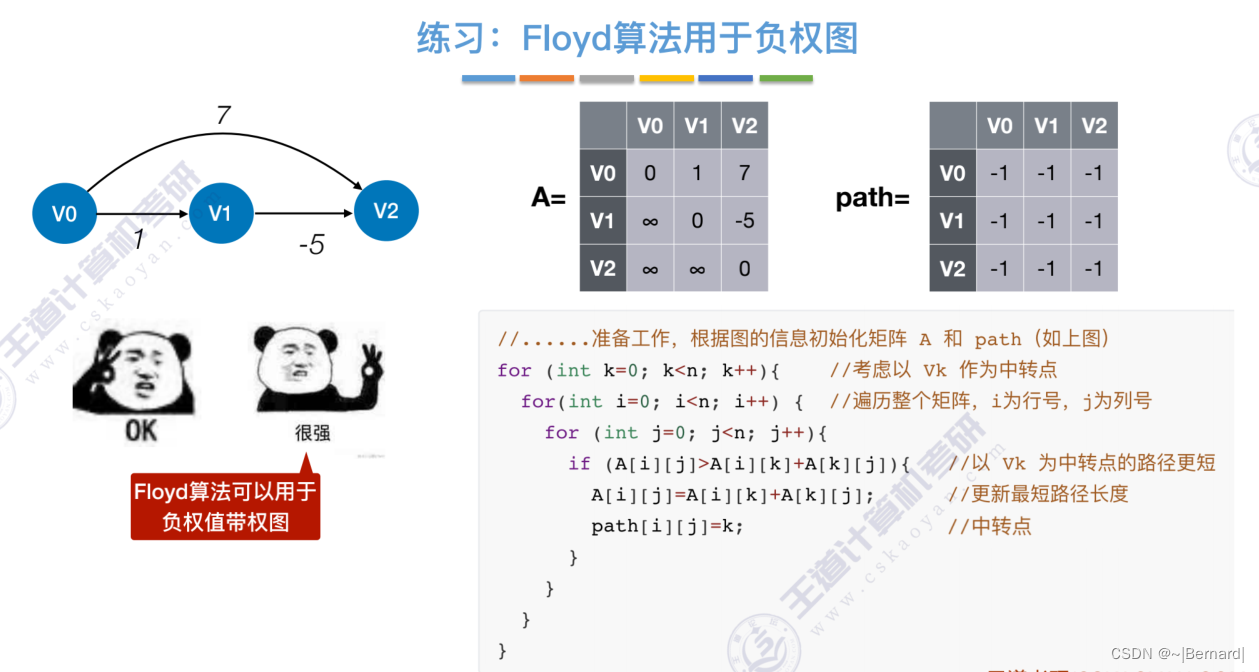
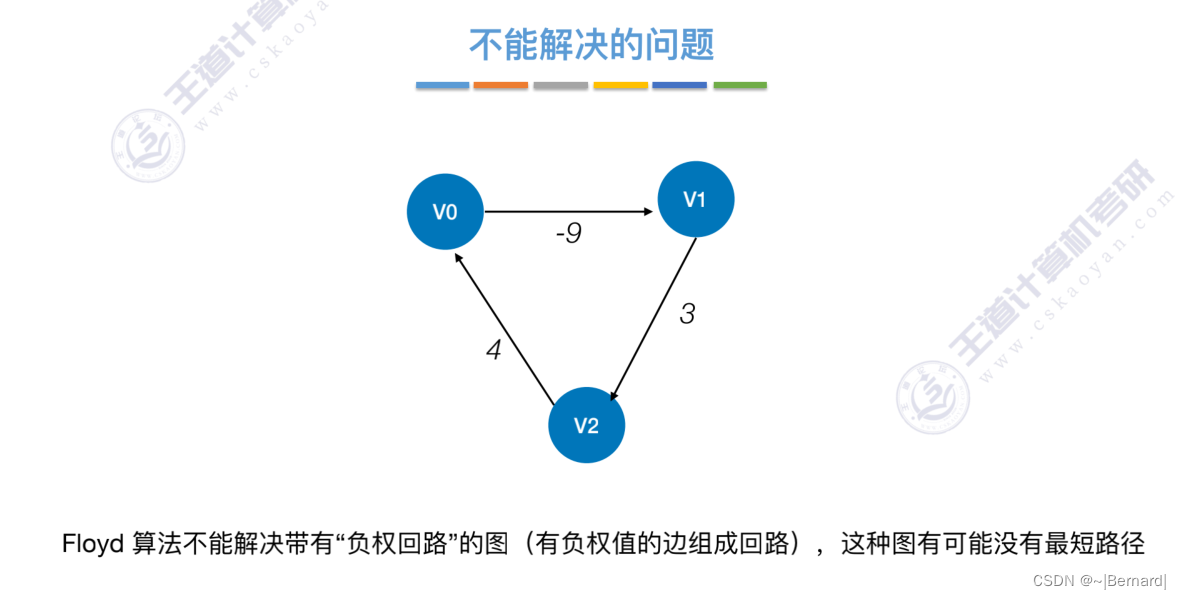
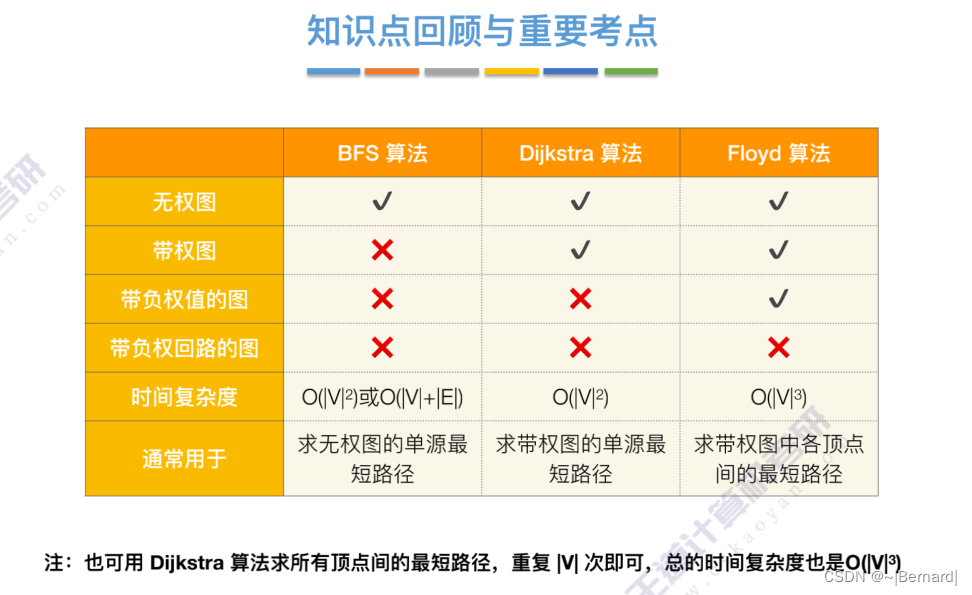
 6.4.4 最短路径问题(Floyd算法)

 

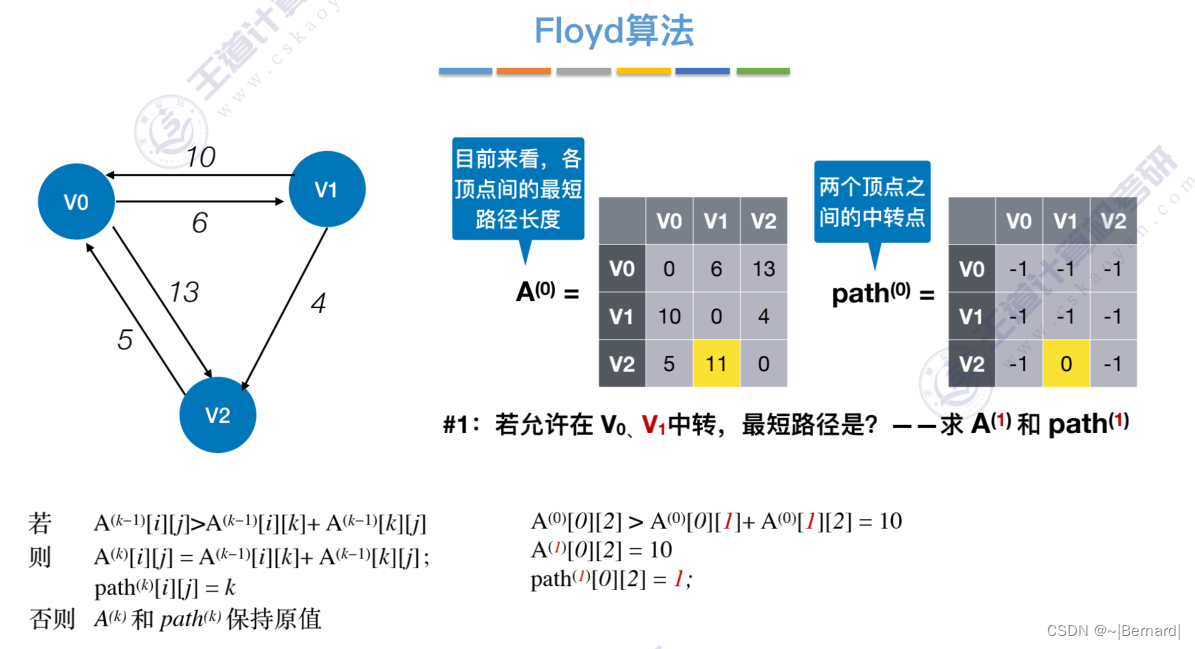
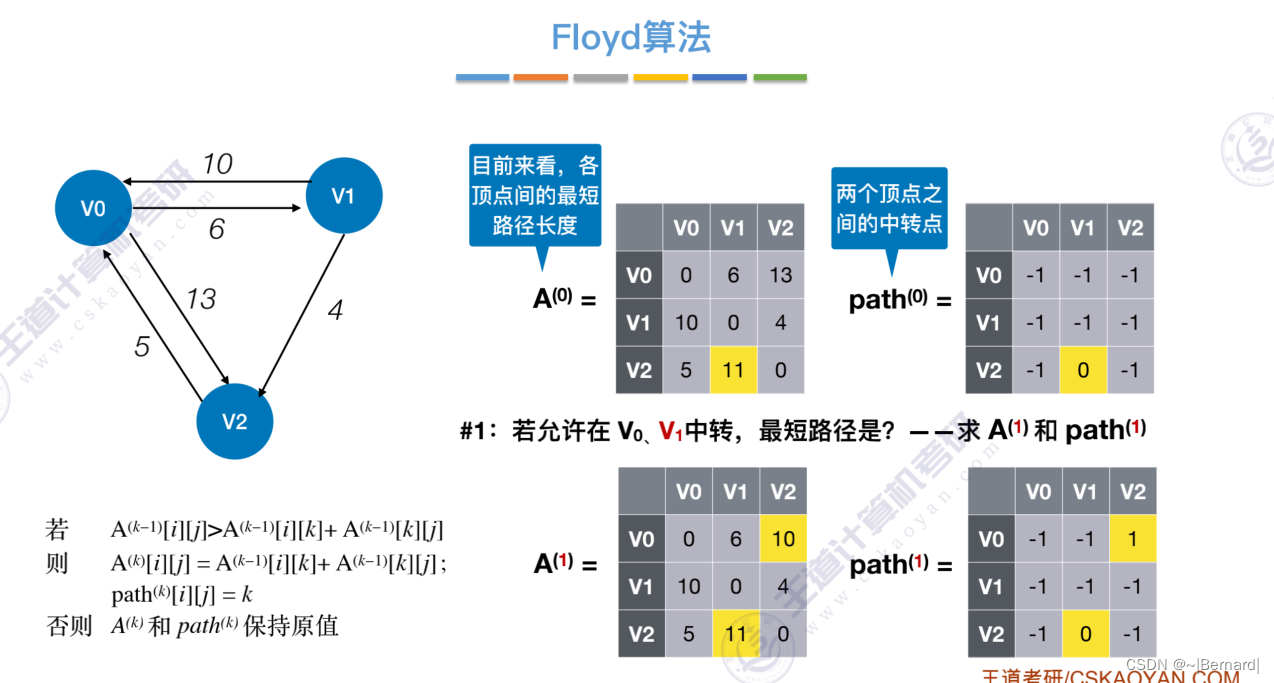
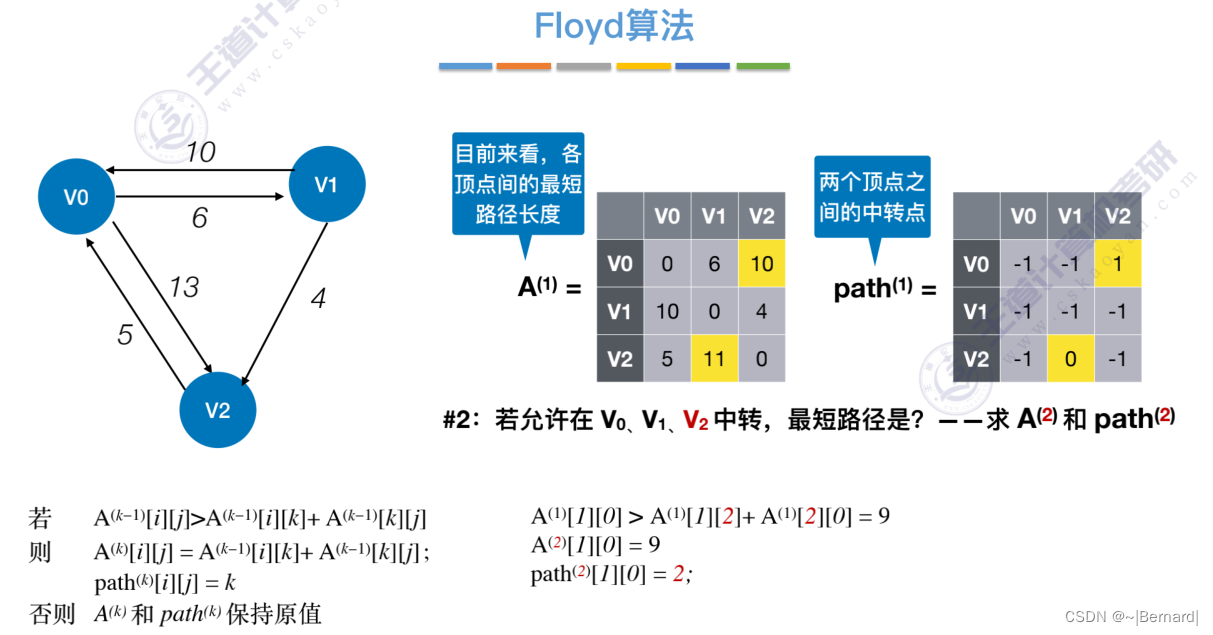
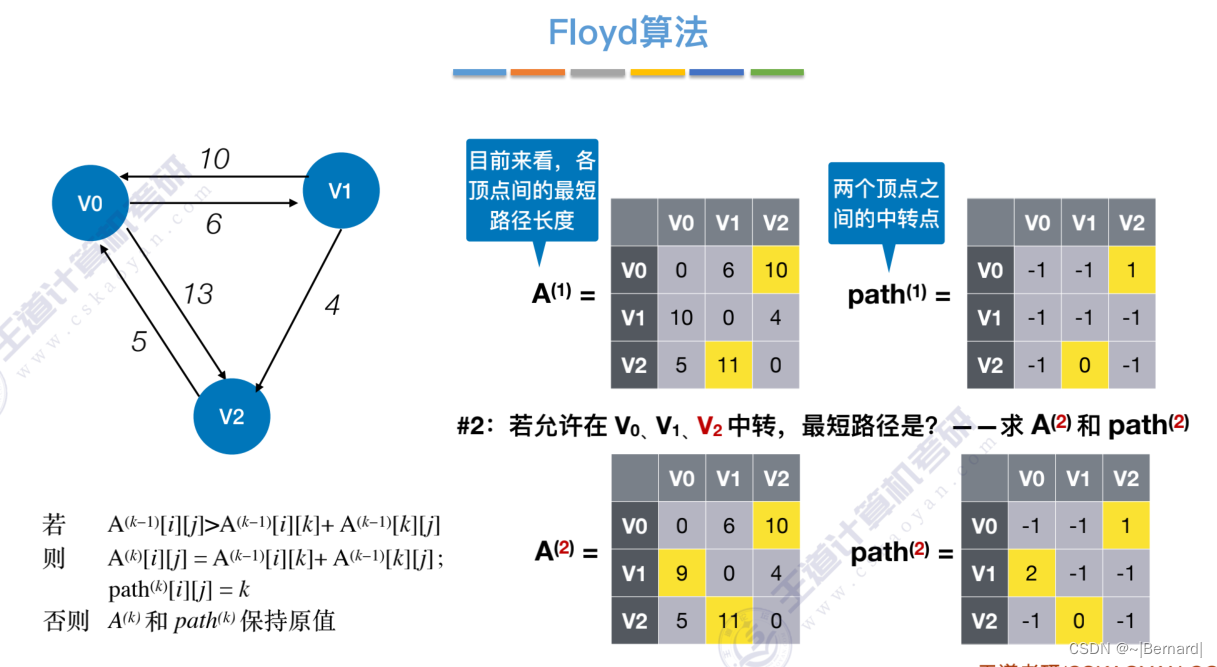
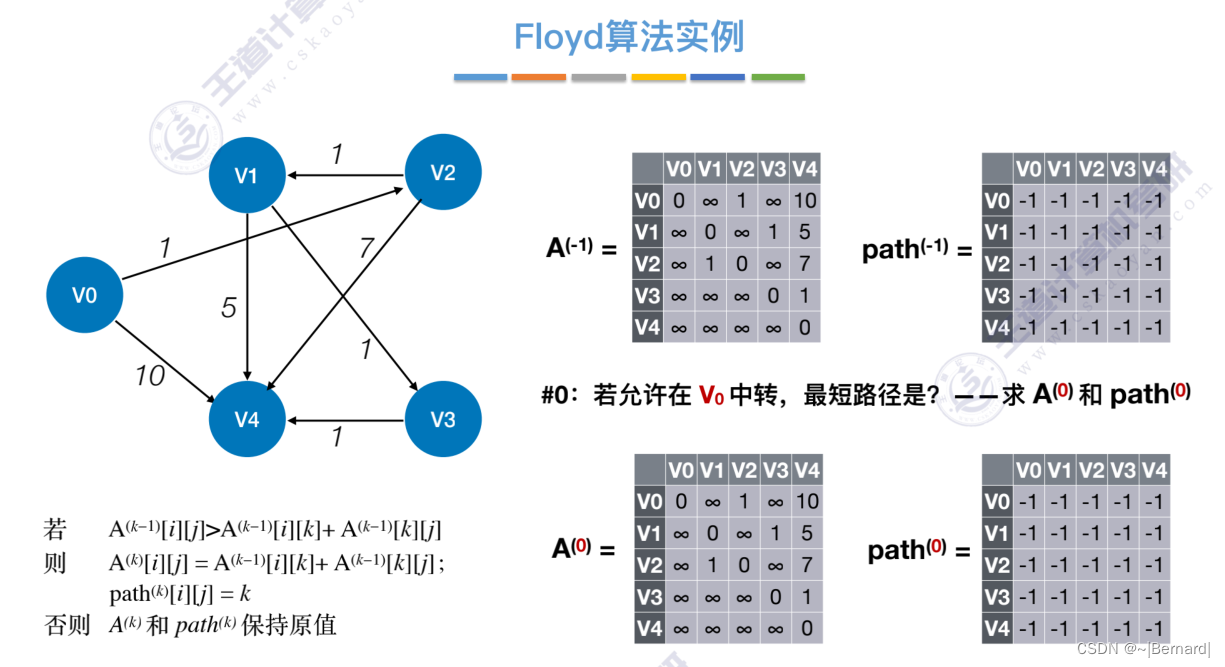
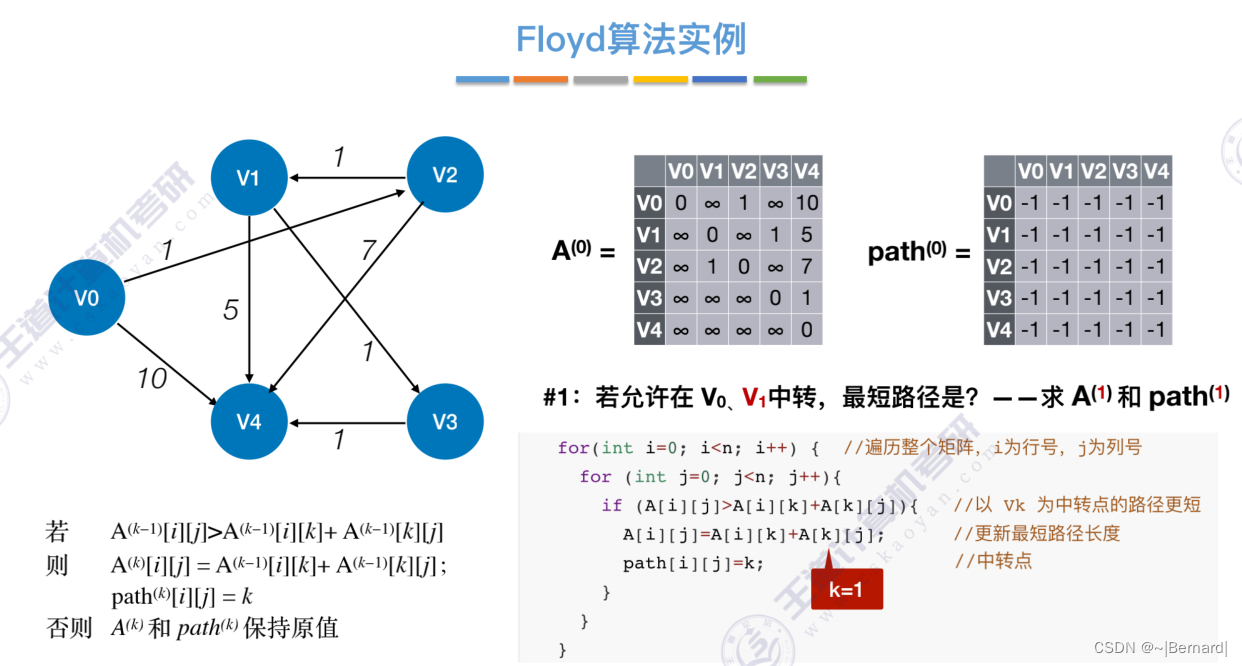
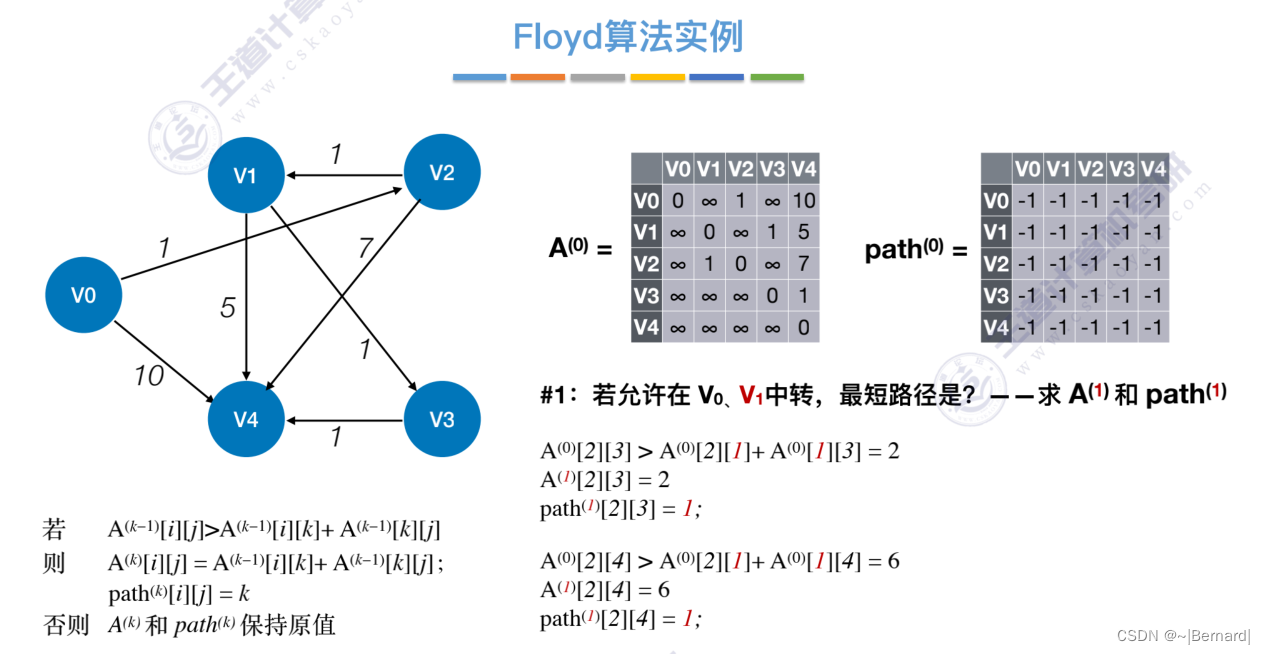
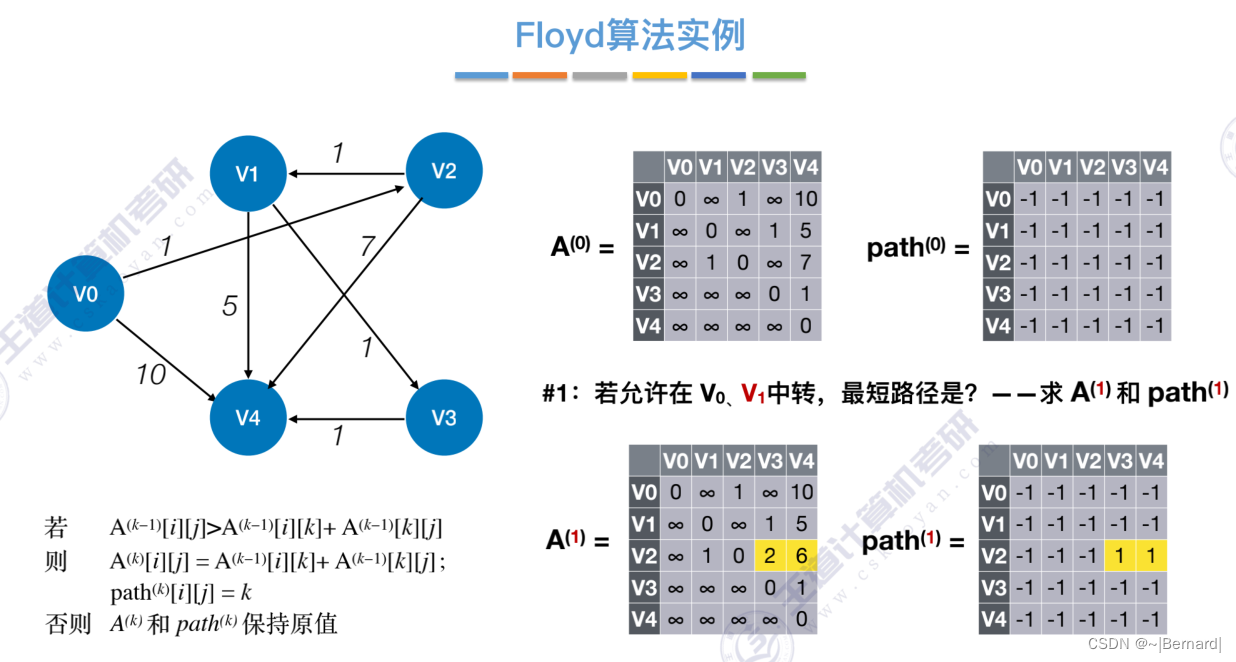
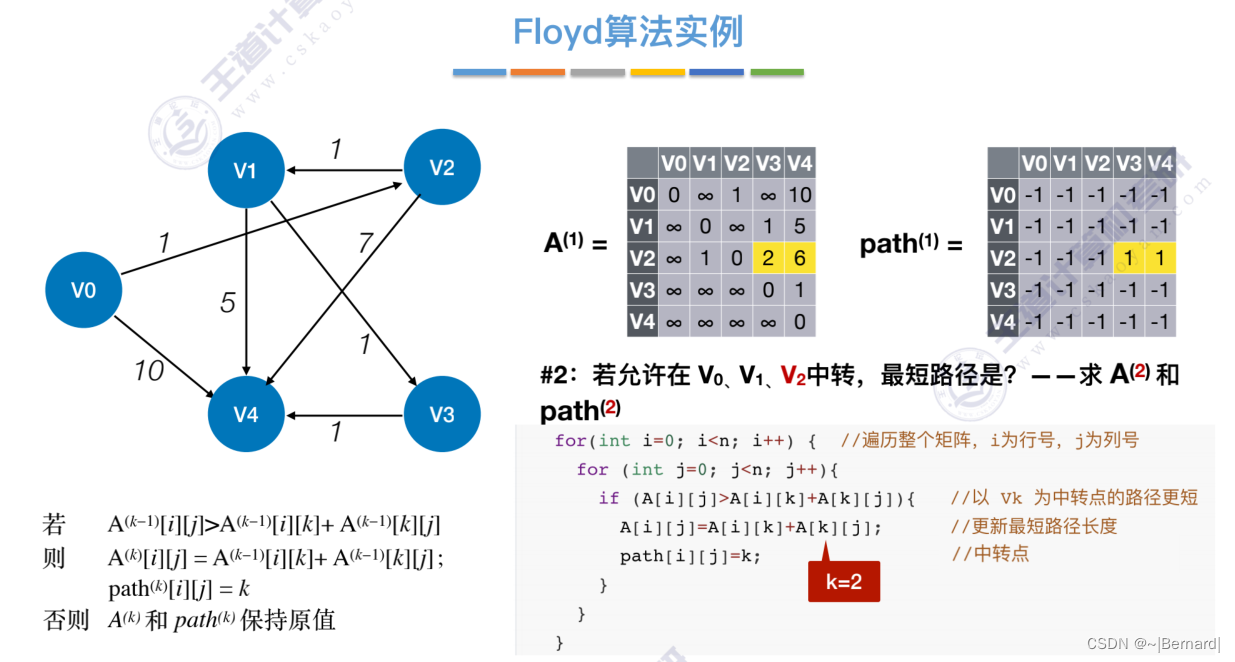
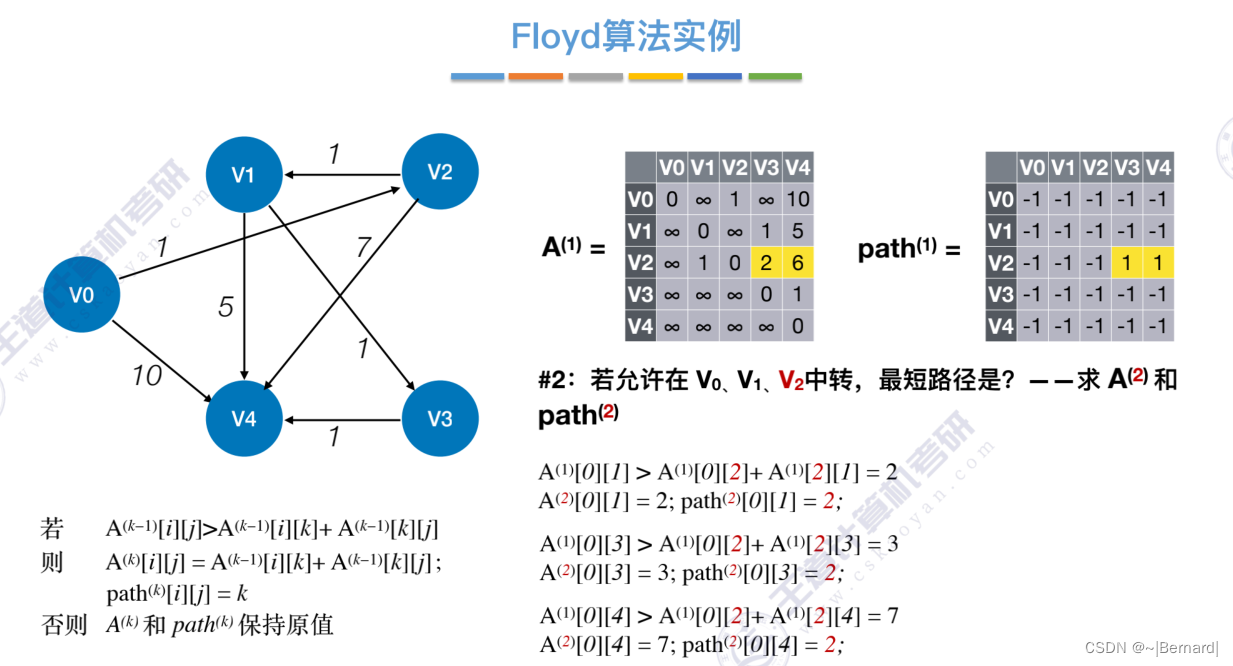
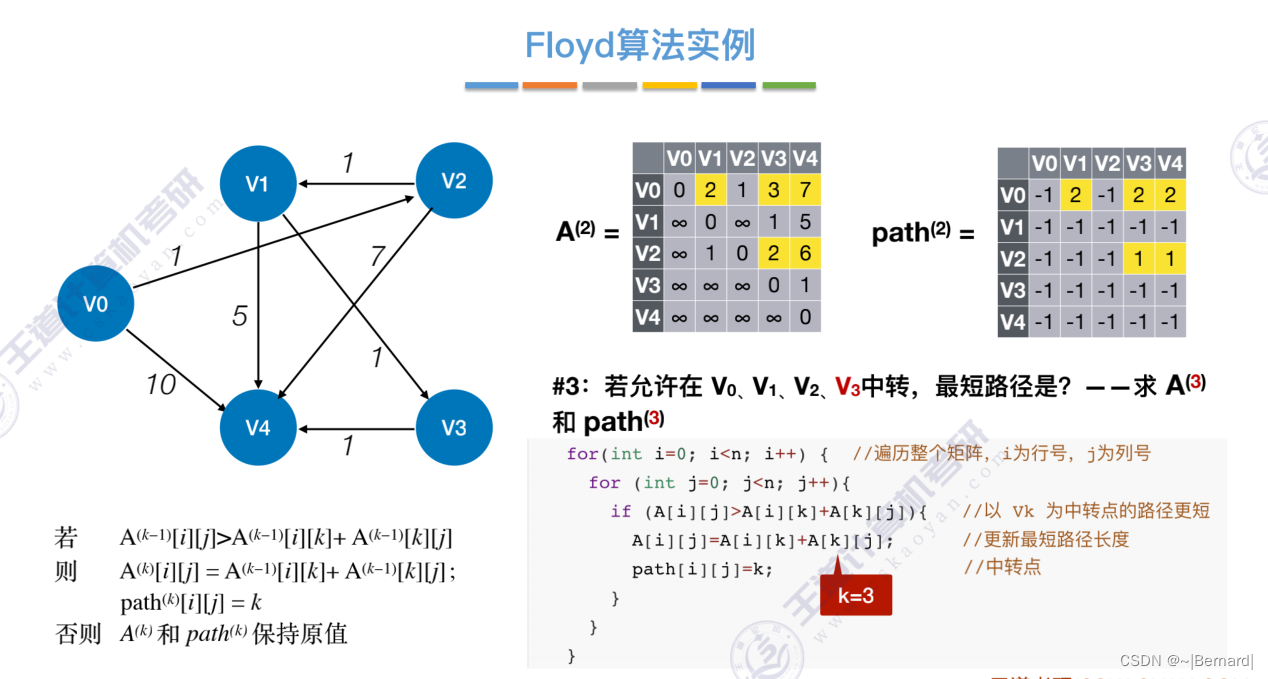
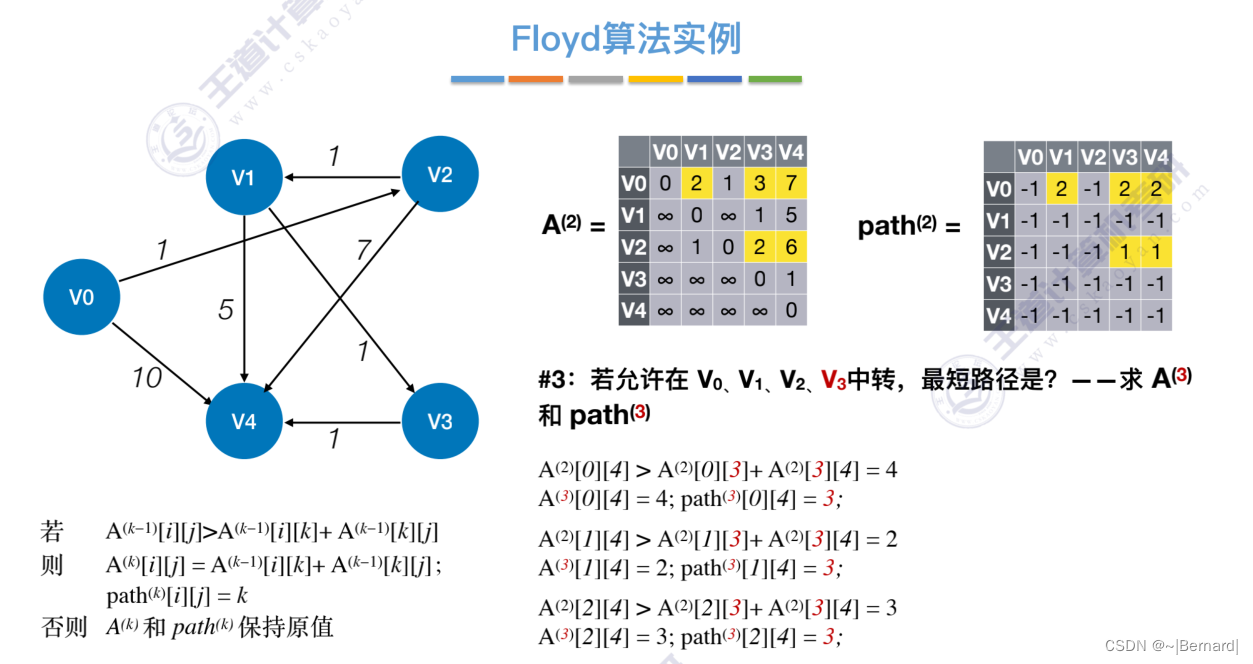
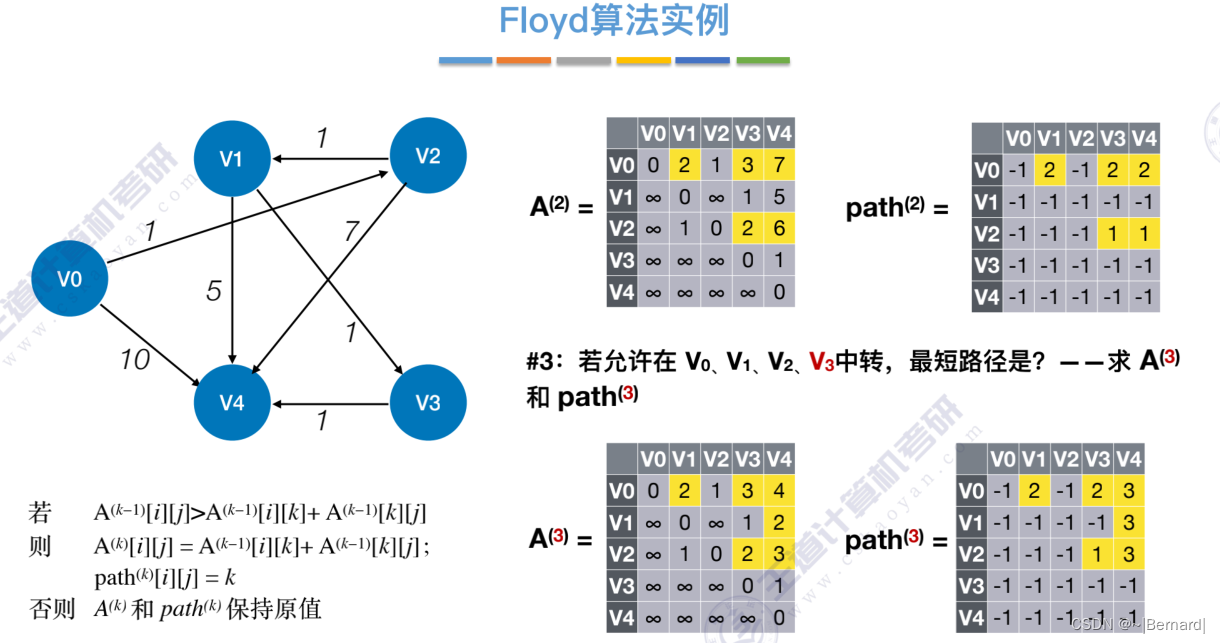
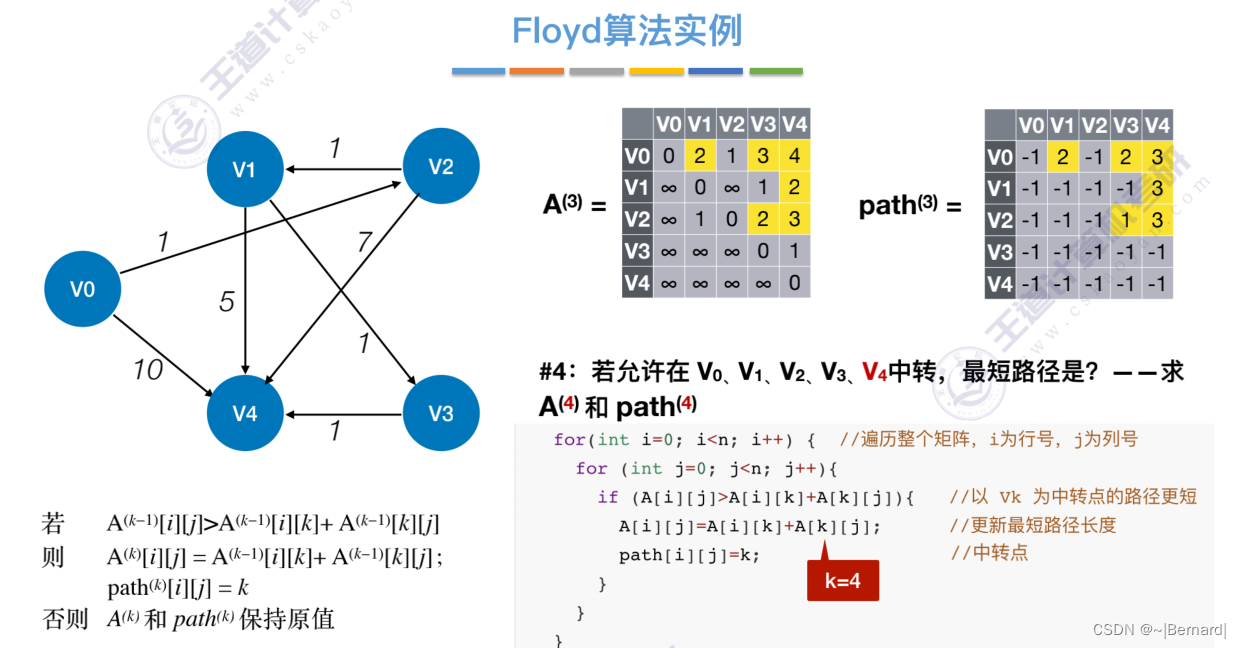
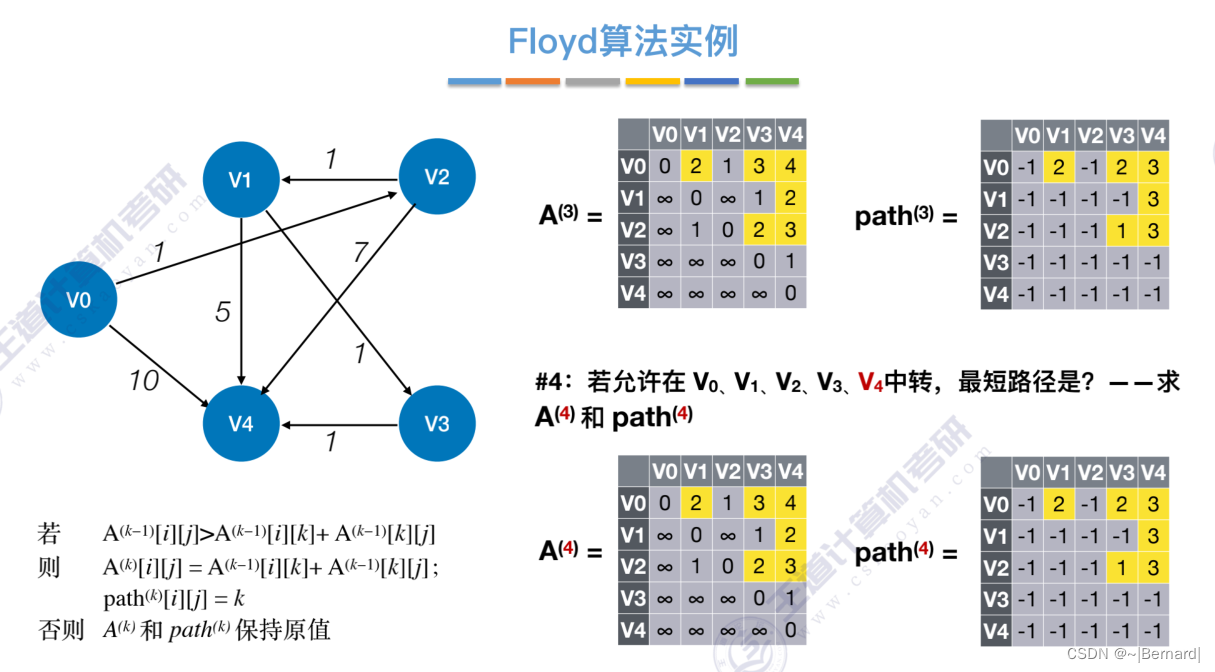
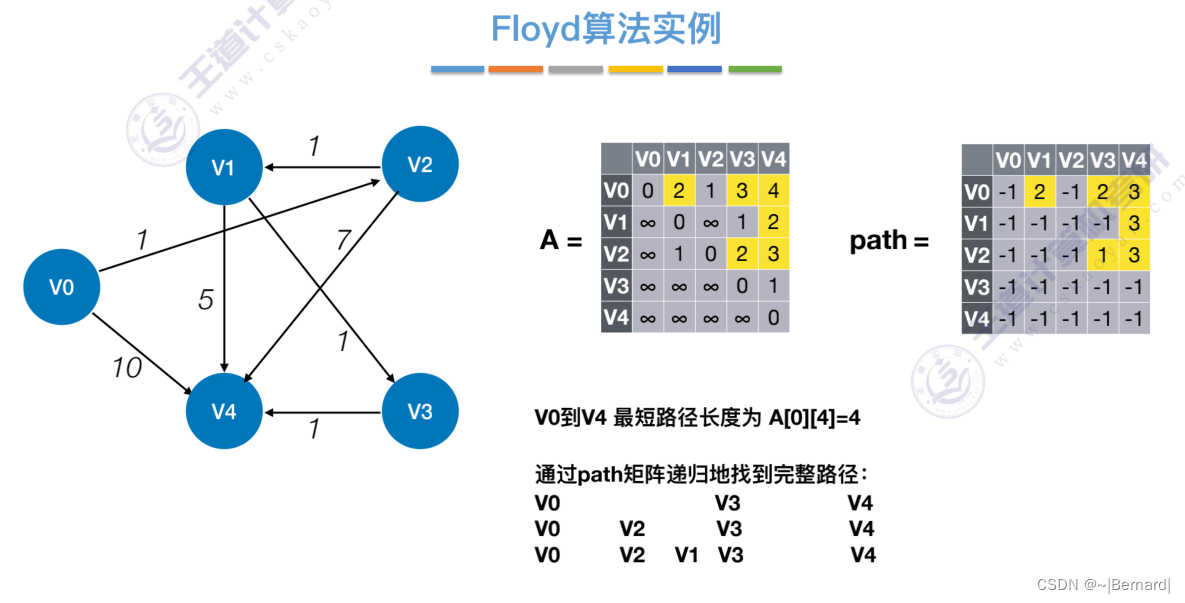
 6.4.5 有向无环图描述表达式

 

 

 

 

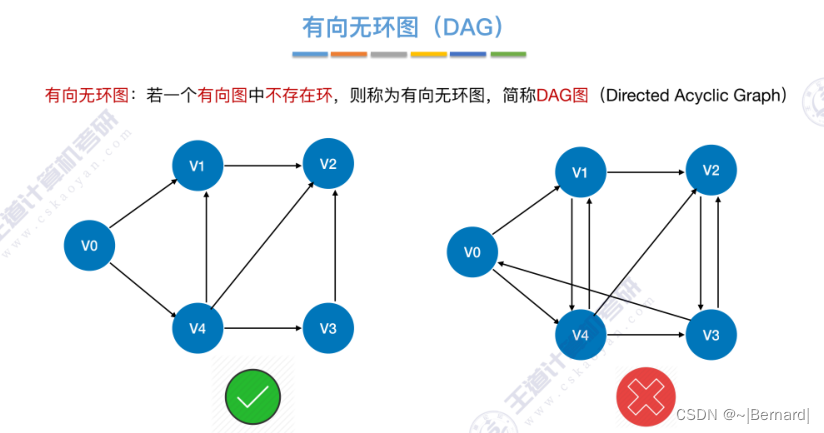
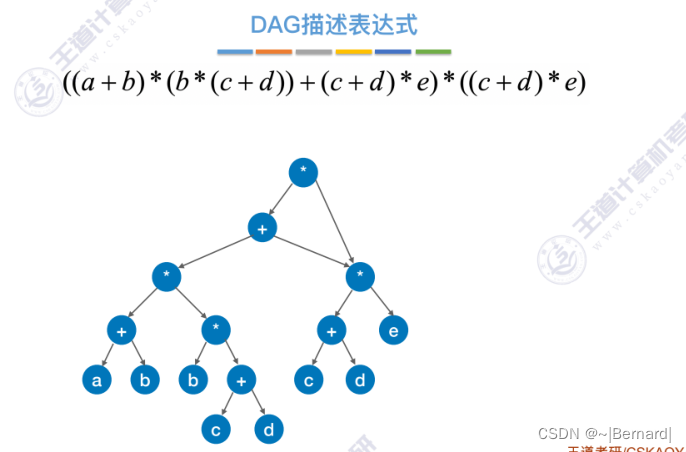
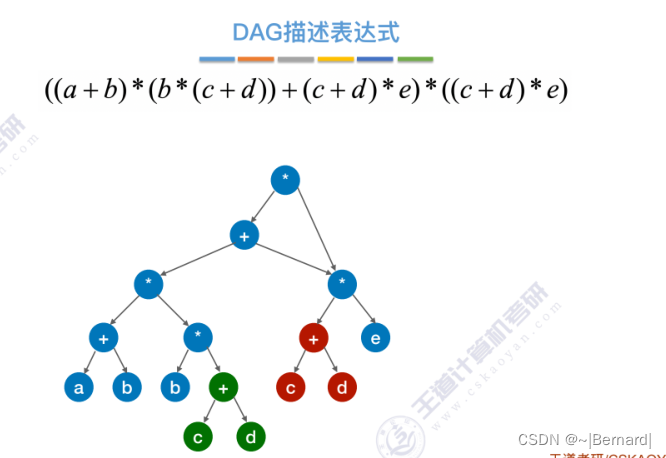
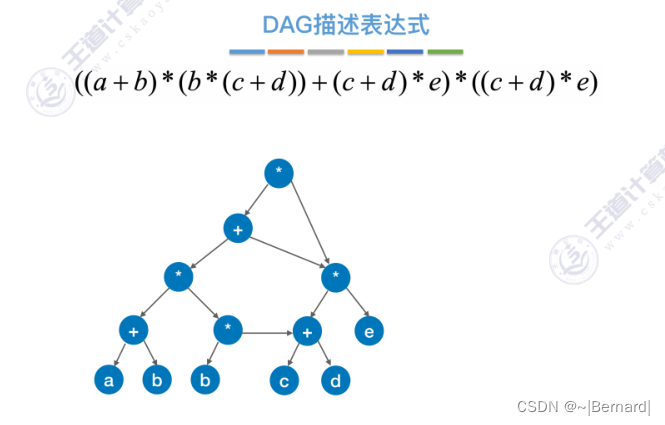
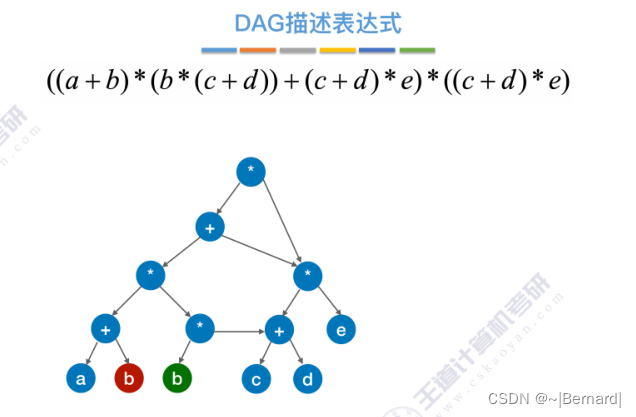
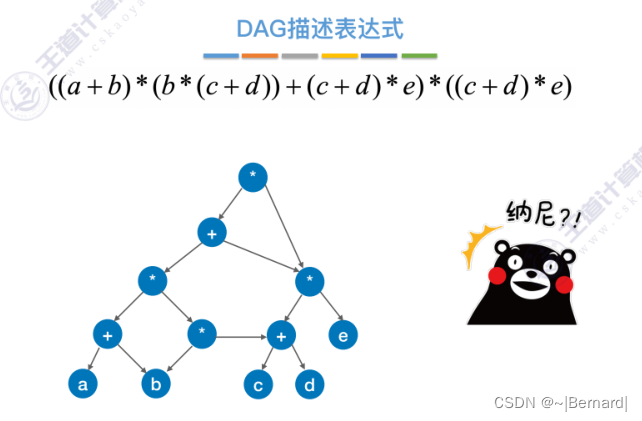
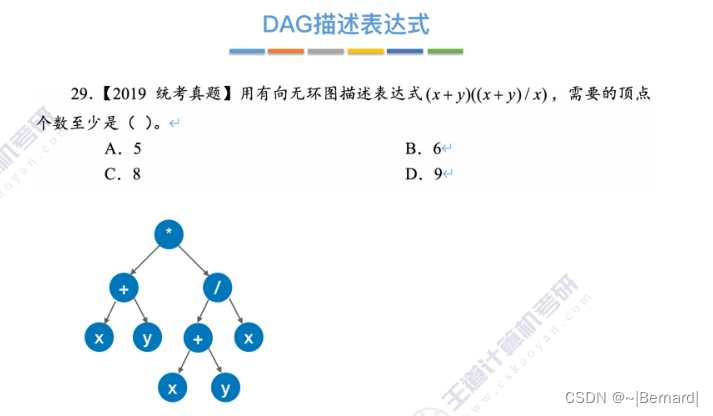
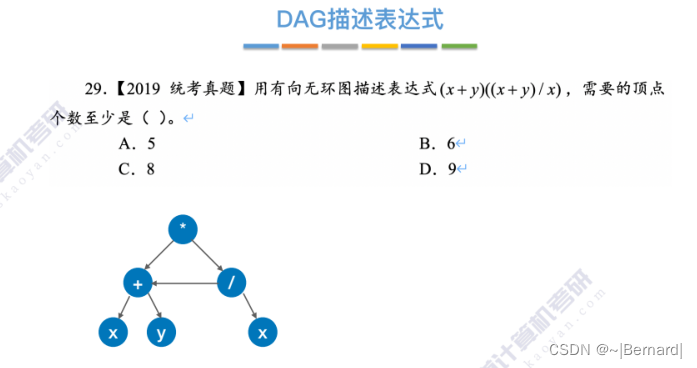
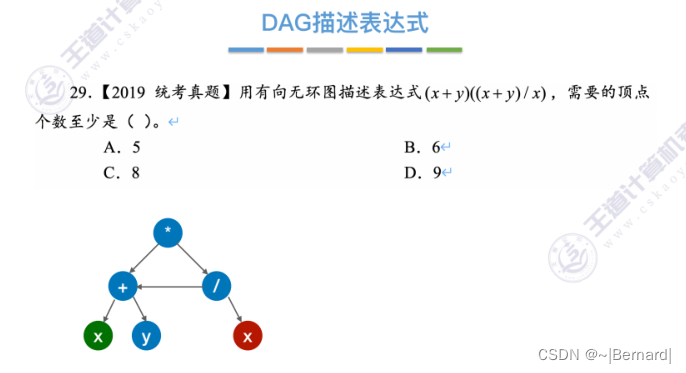
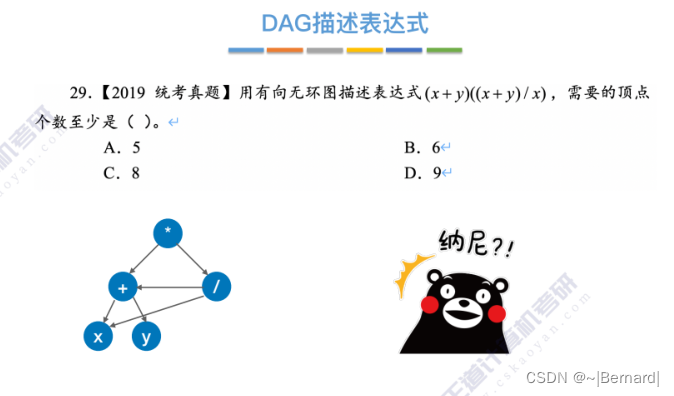
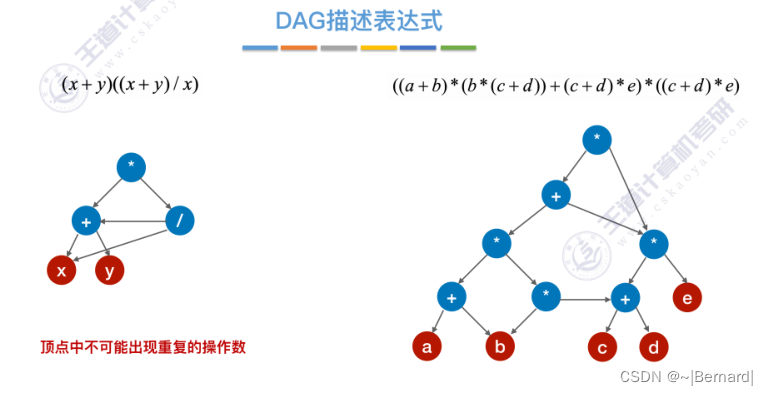
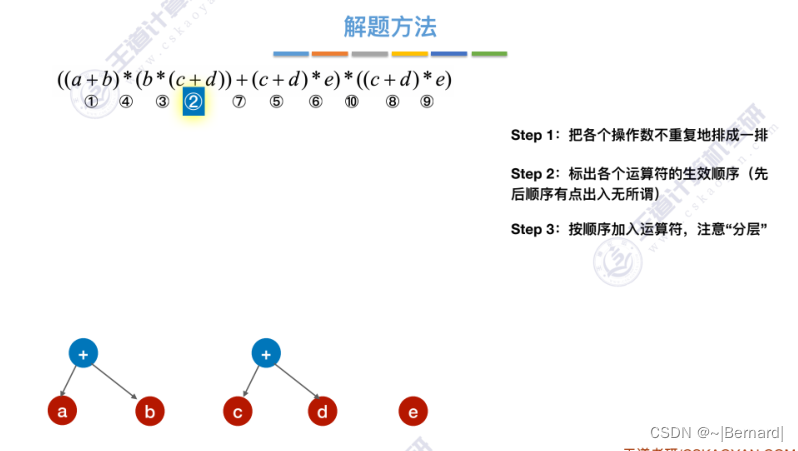
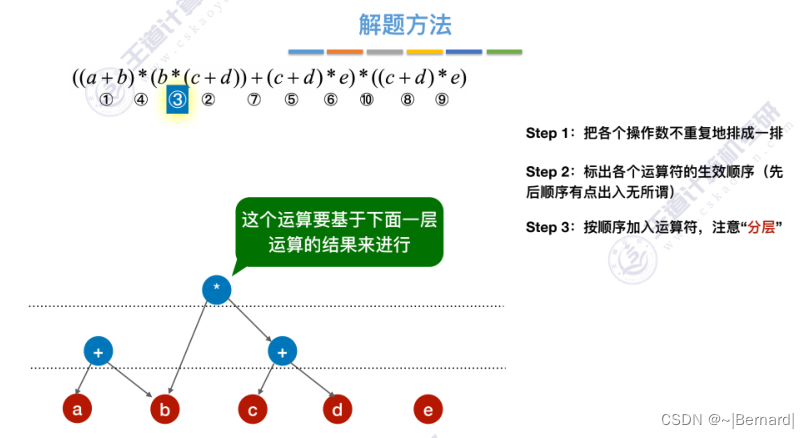
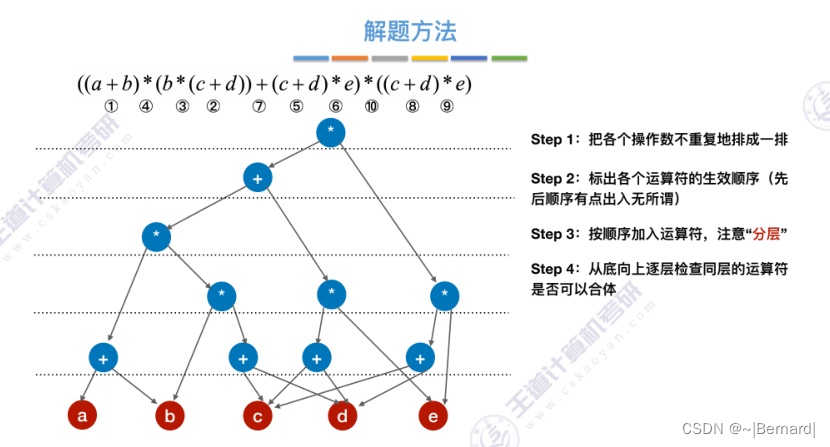
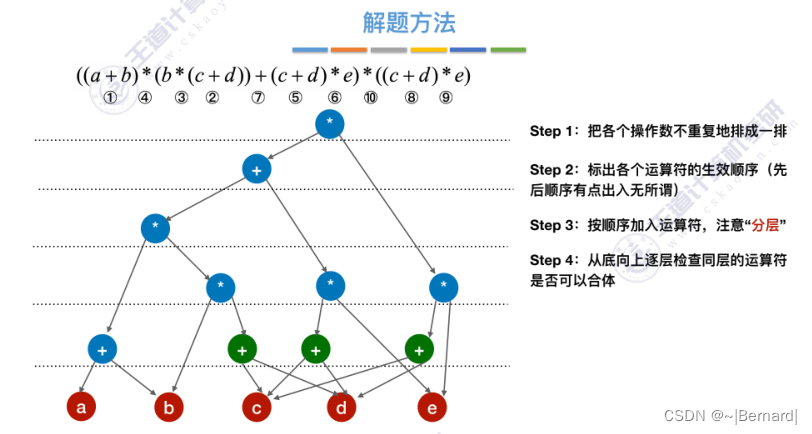
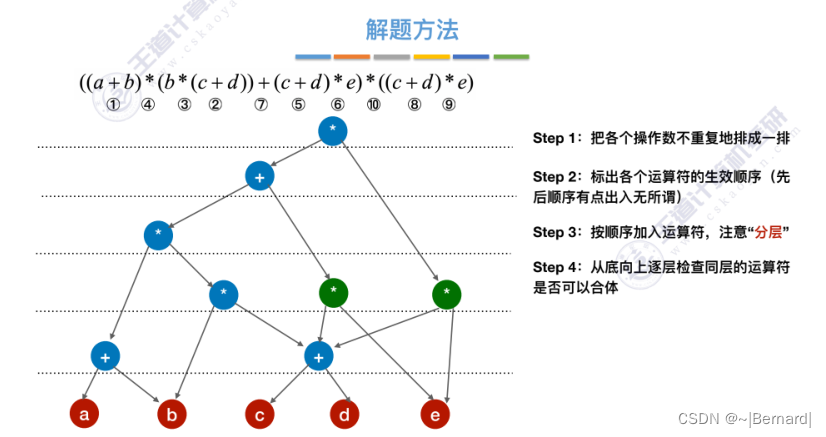
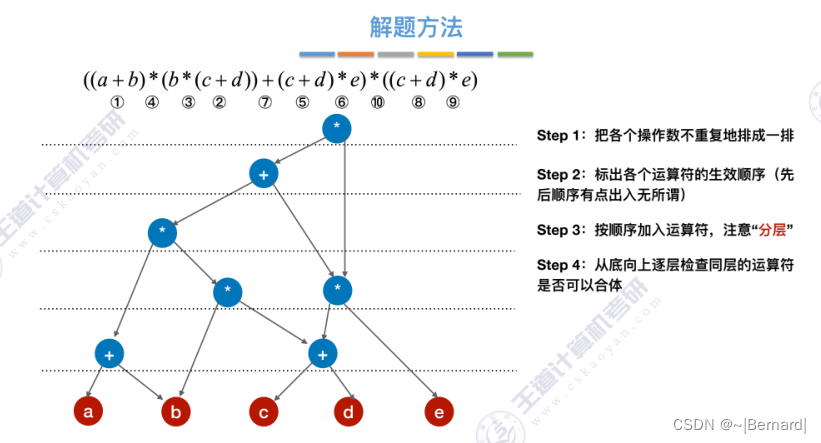
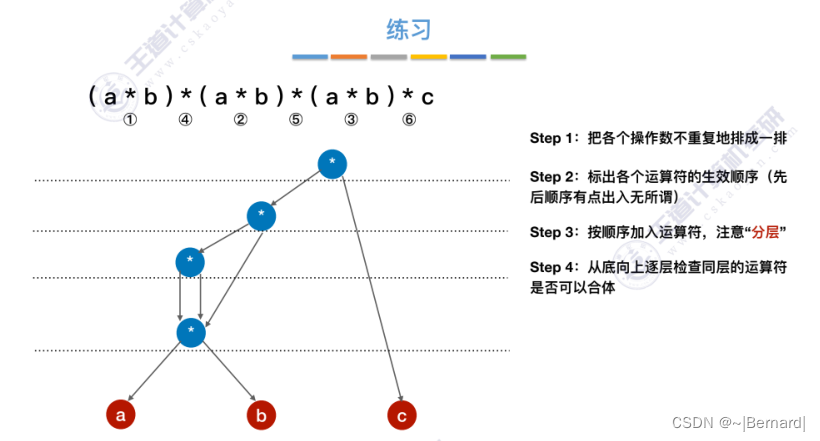
 6.4.6 拓扑排序

 

 

 

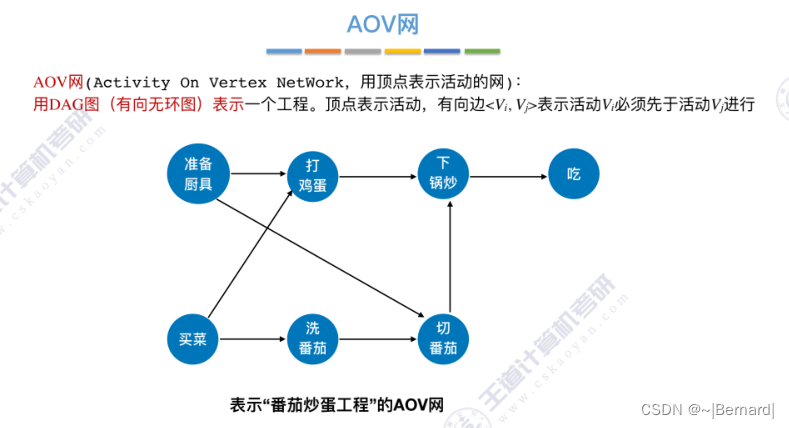
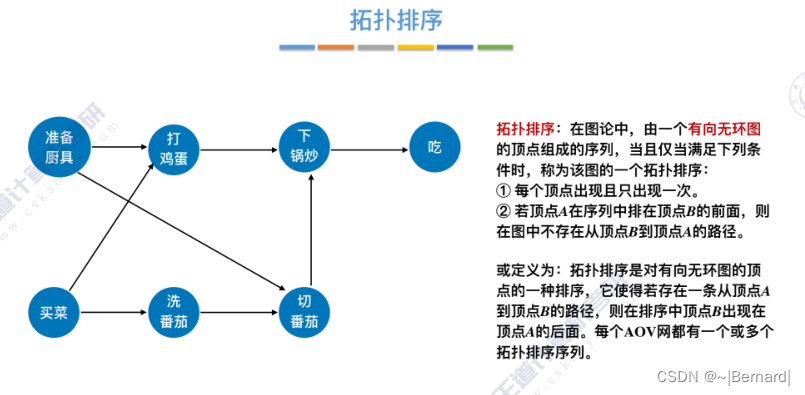
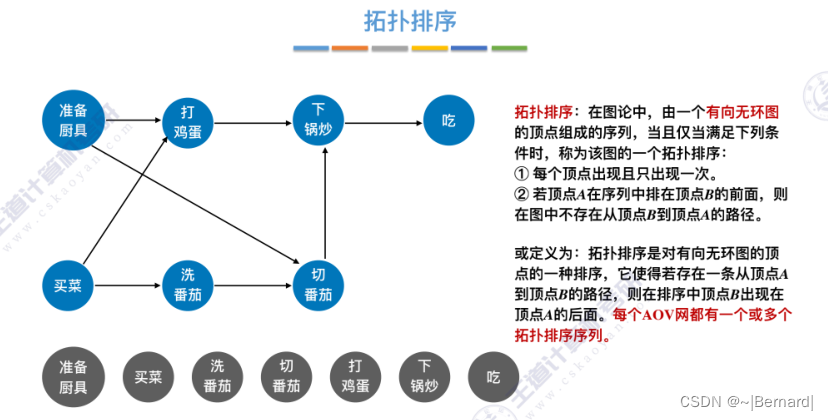
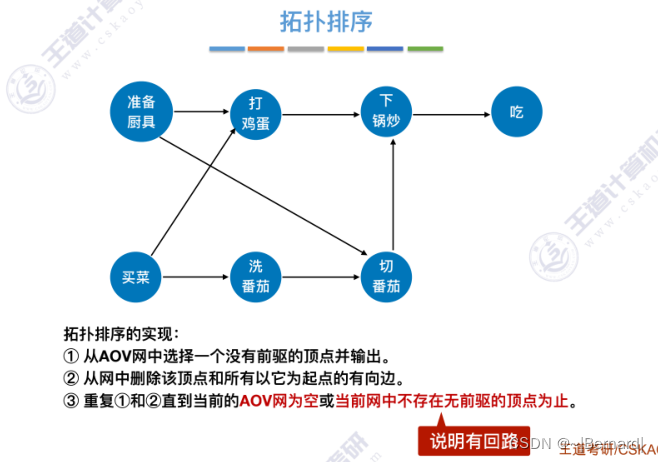
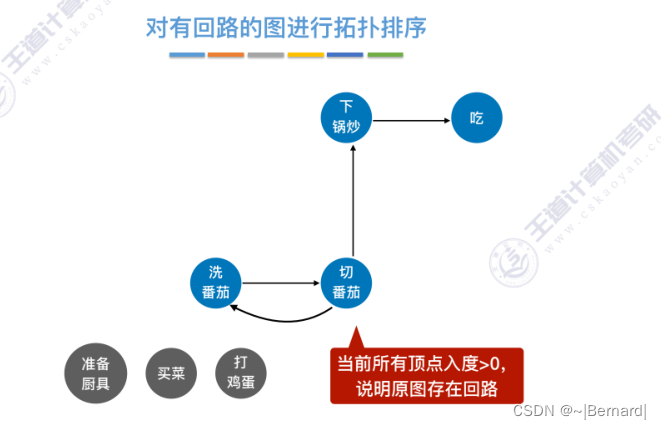
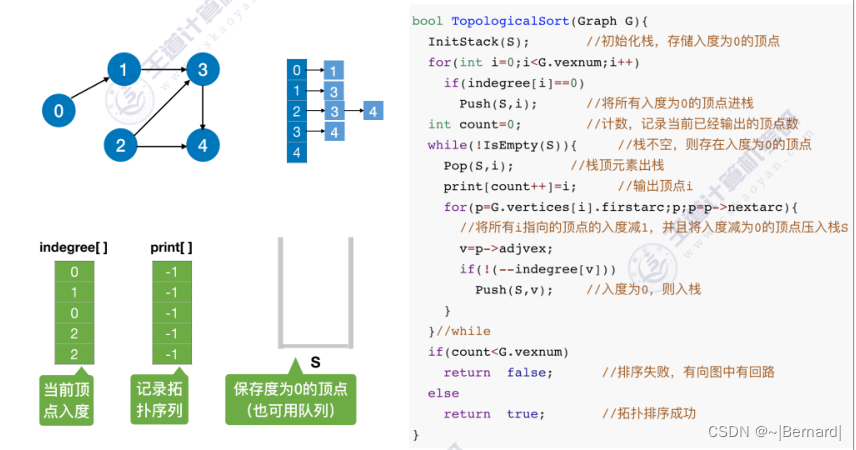
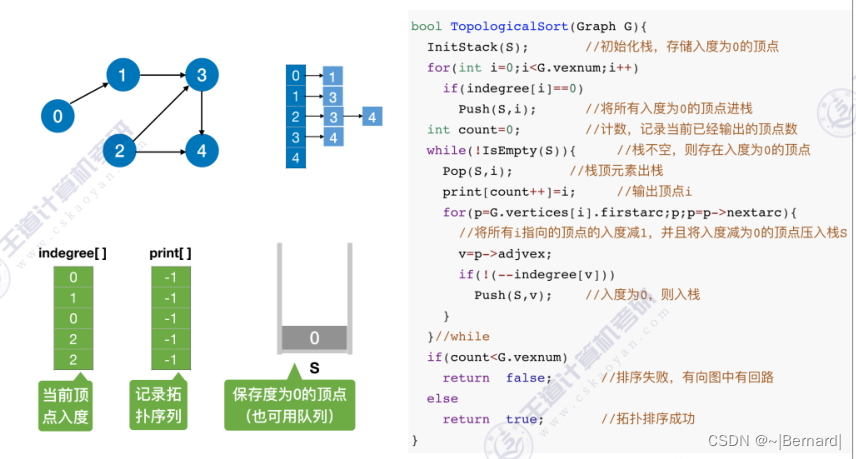
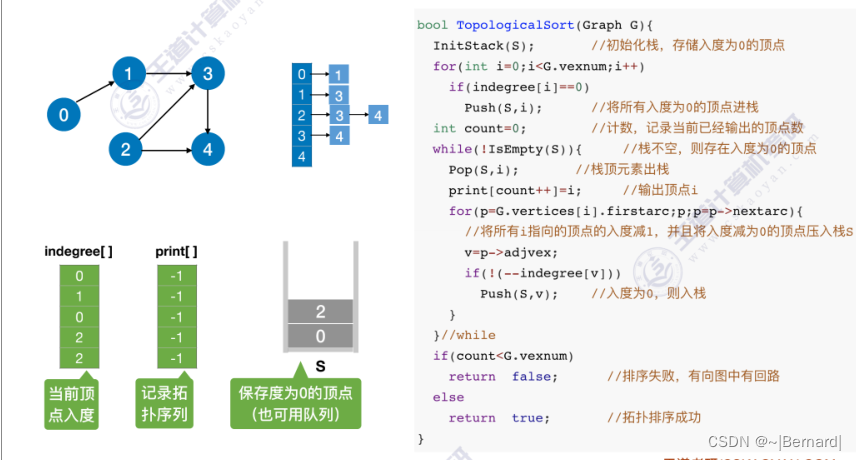
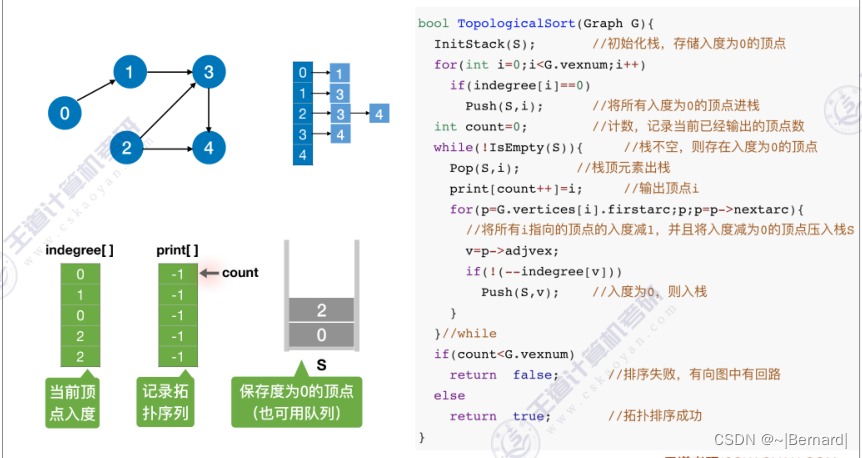
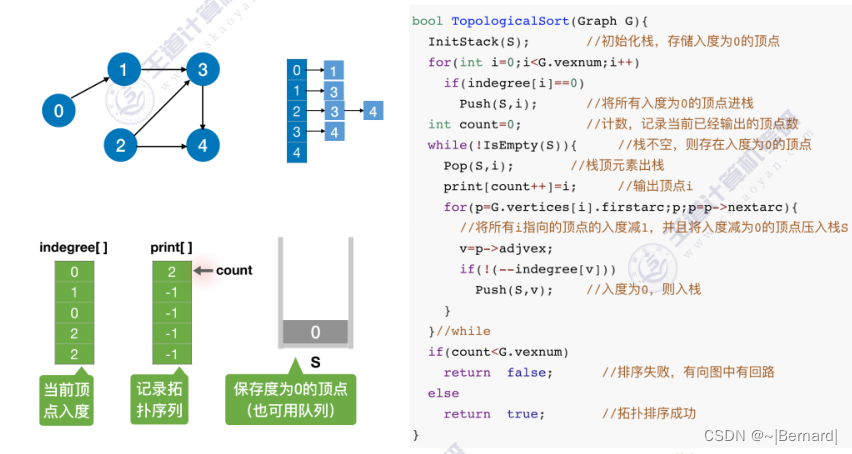 关于拓扑排序的程序堆栈流程查看王道对应课件。

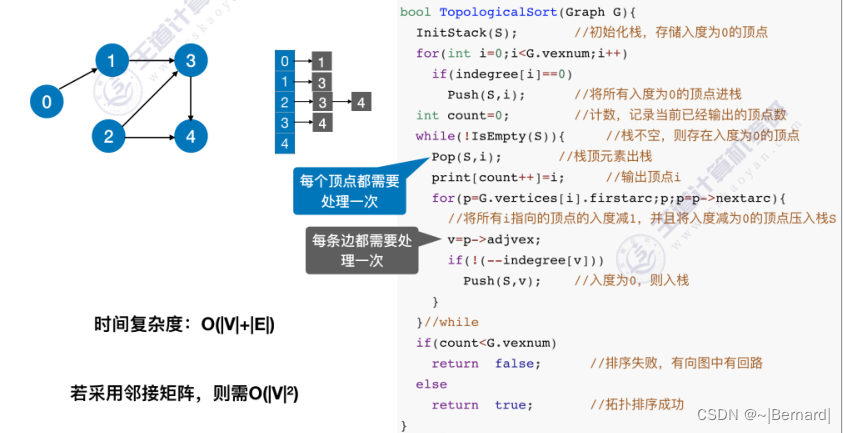
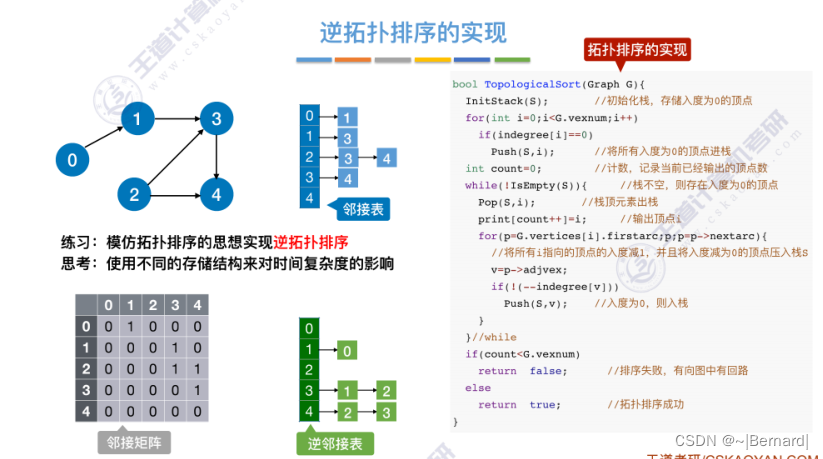
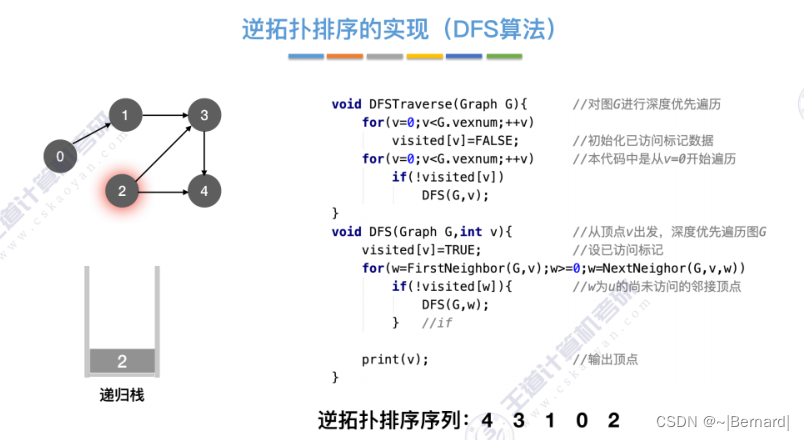 关于逆拓扑排序的堆栈细节查看王道课件

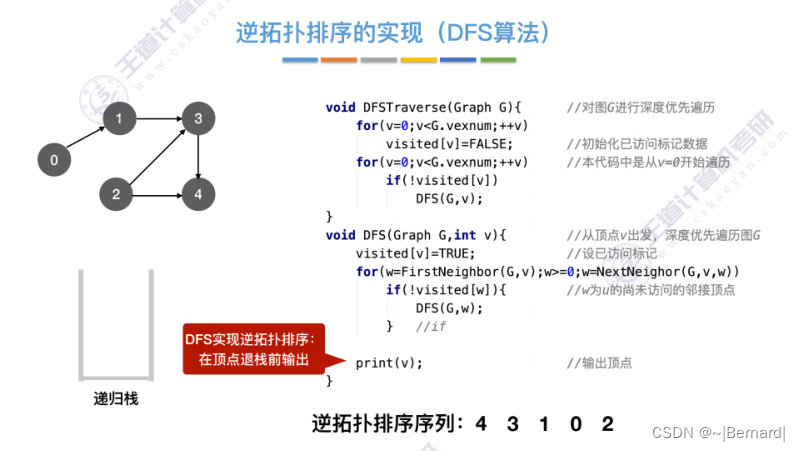
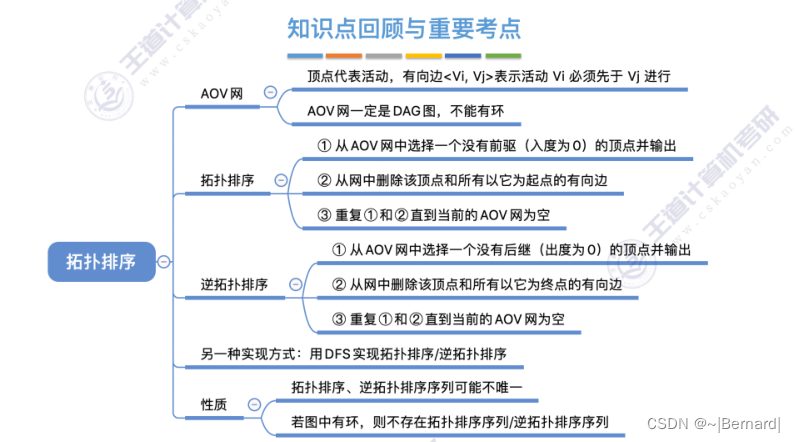
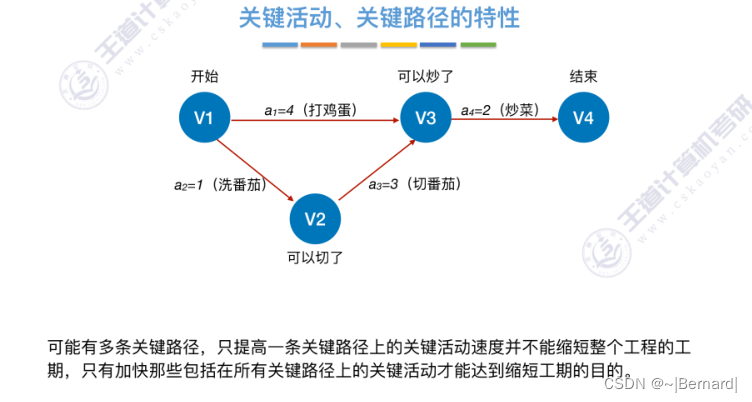
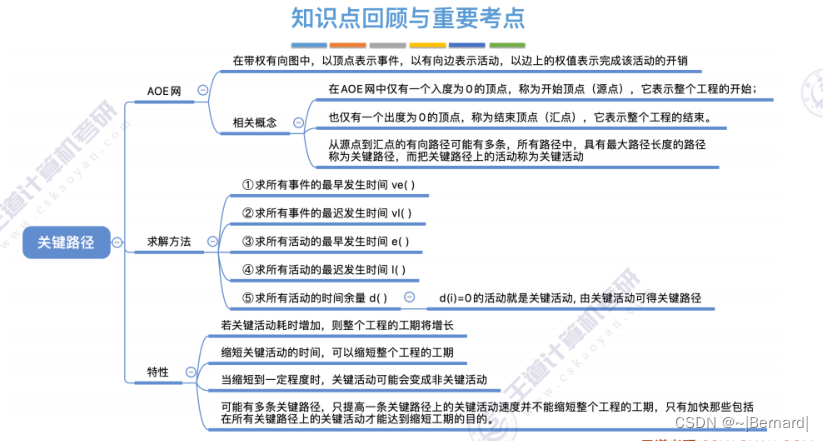
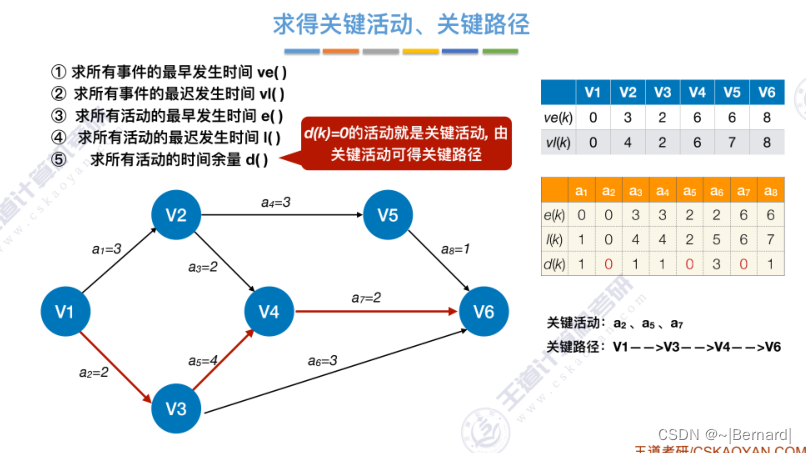
 6.4.7 关键路径

 

 

 

 

 

 

 

 

 

 

 

 

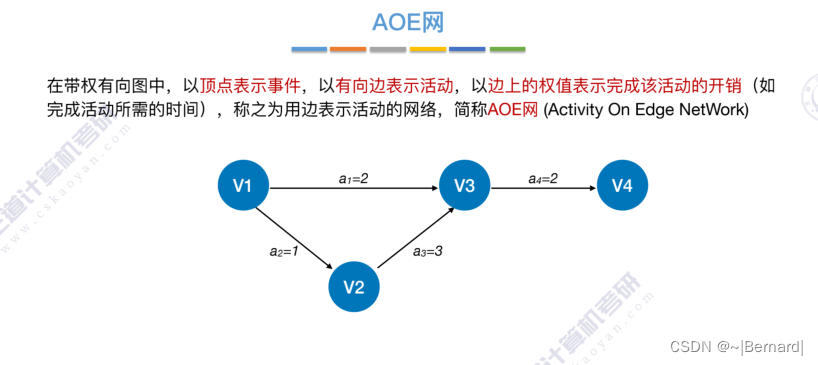
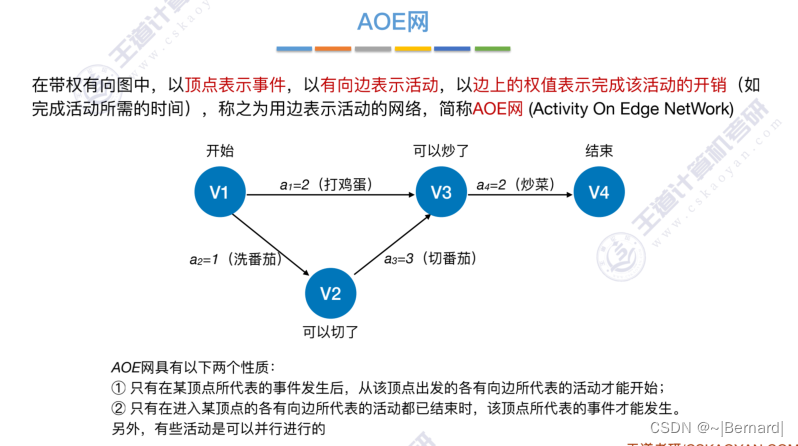
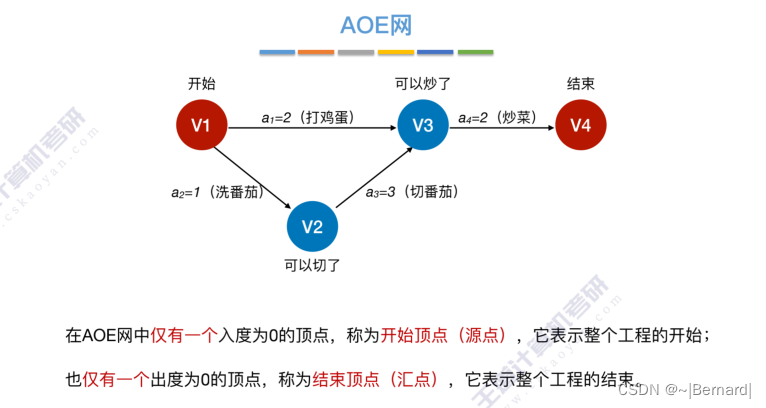
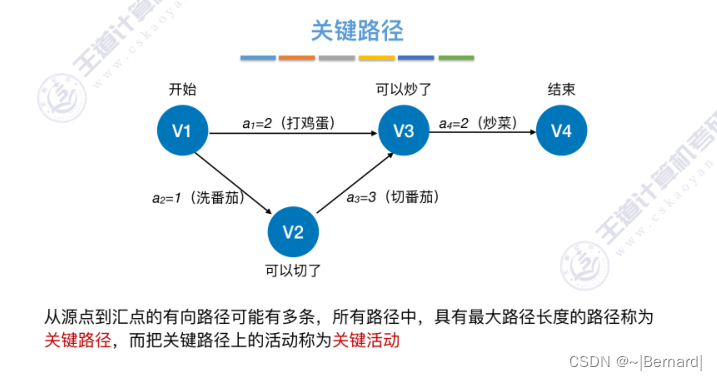
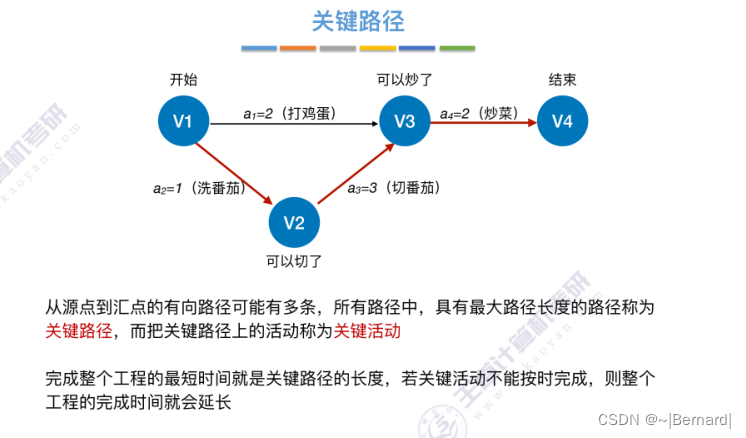
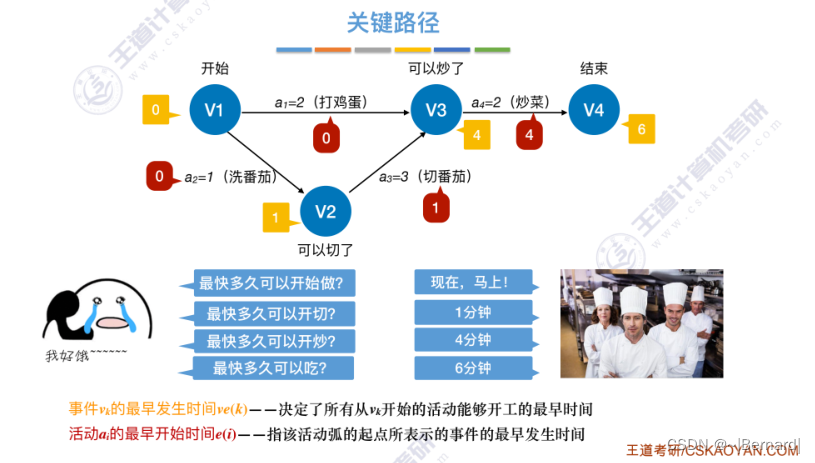
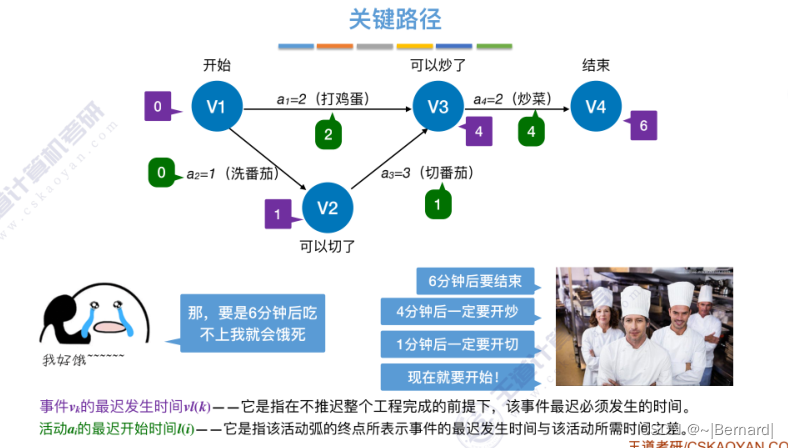
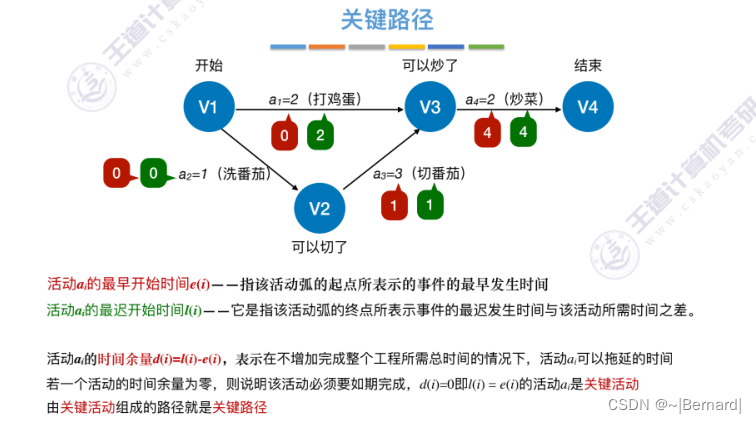
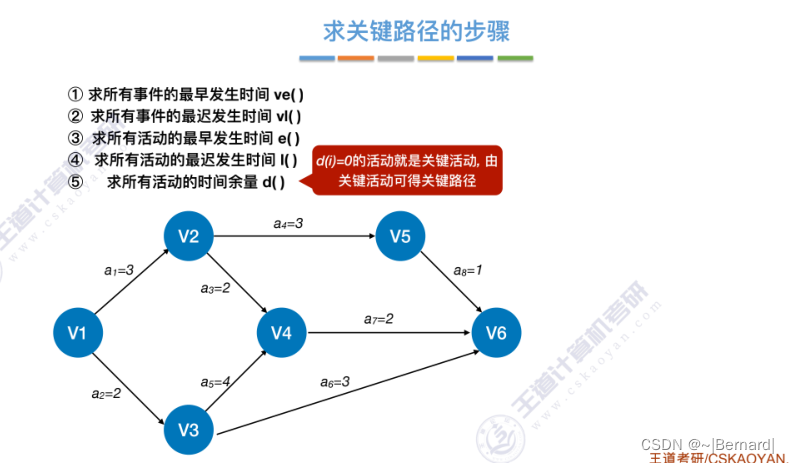
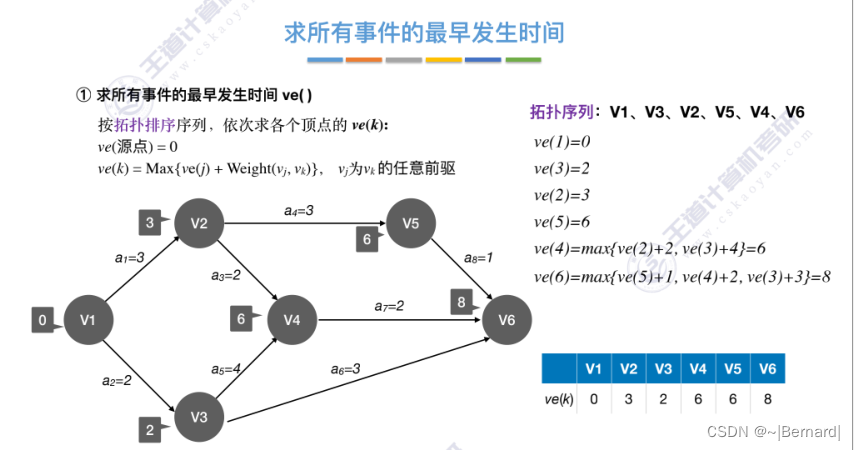
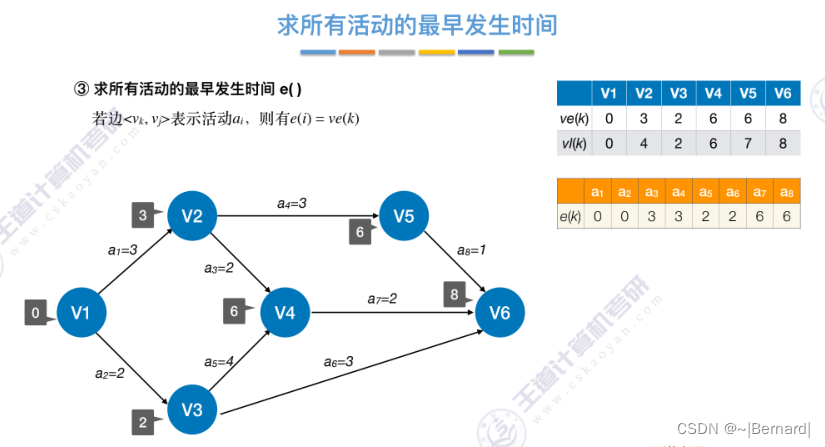
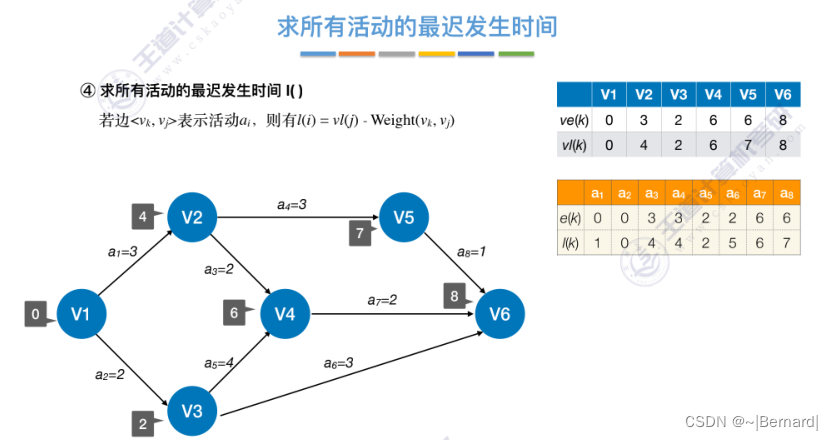
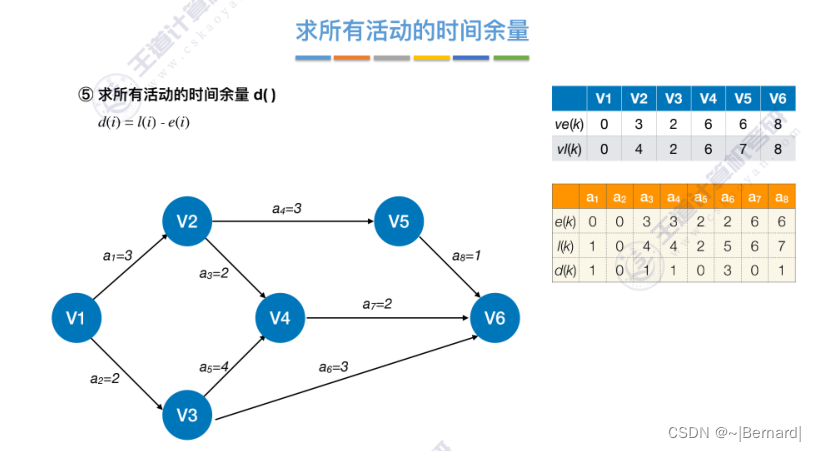 具体算法细节见王道课件

 

 

 

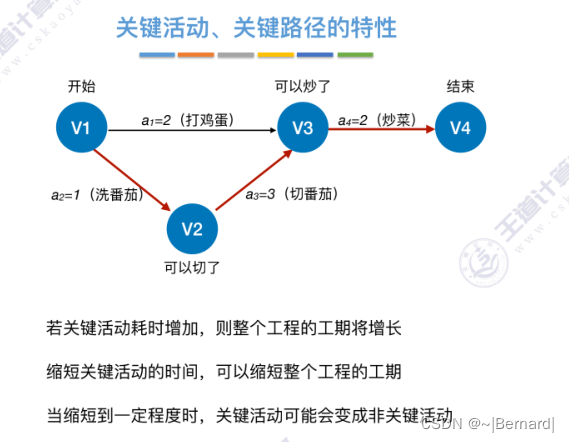
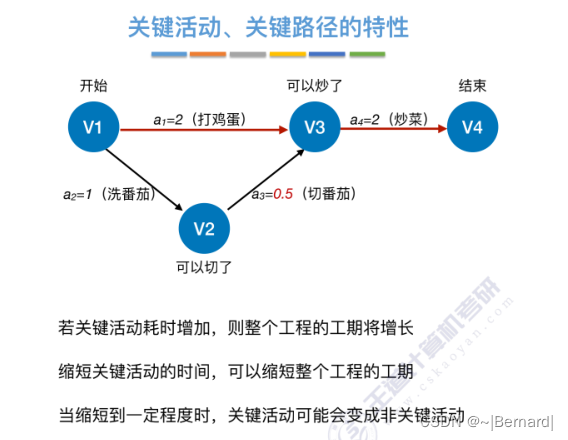
若将切番茄这个活动缩短为0.5，那整个切番茄的活动就变成了非关键活动