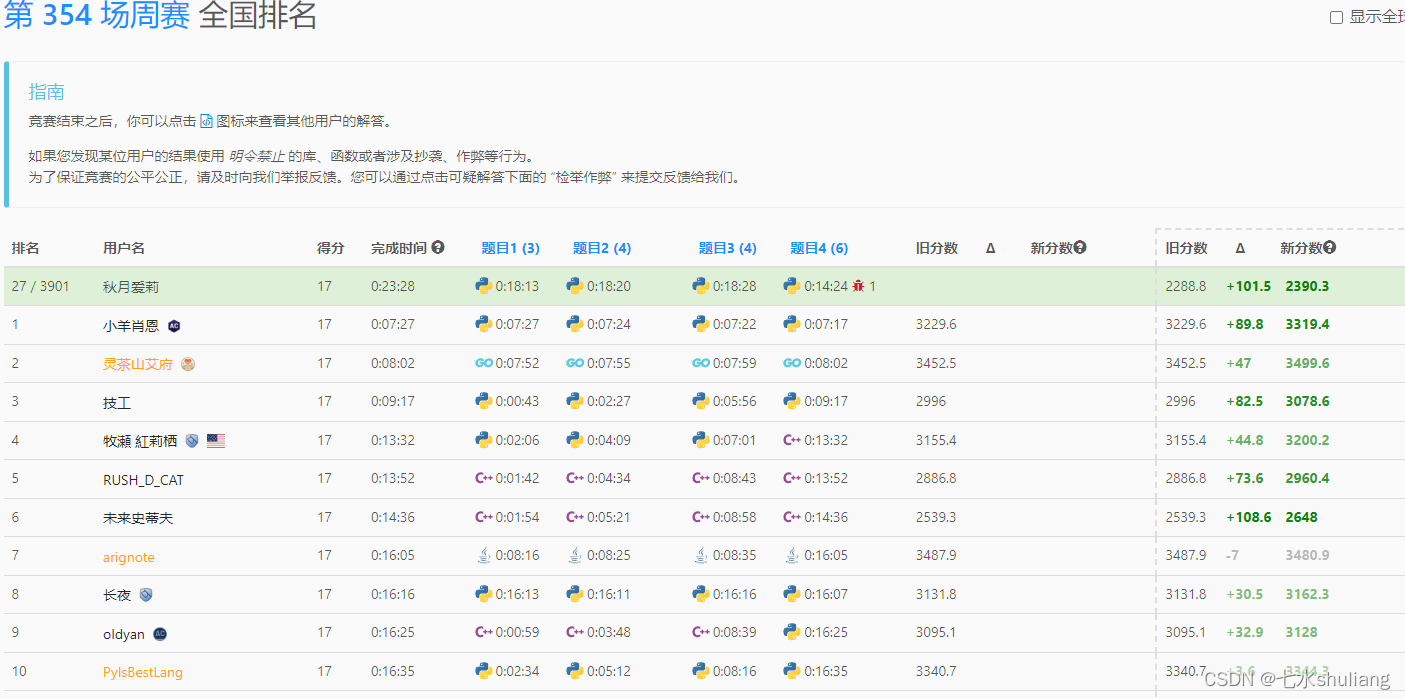
一、本周周赛总结

• T1 模拟。
• T2 RUPQ 差分/树状数组。
• T3 前后缀分解。
• T4 双指针+trie（py负优化）。
  

6889. 特殊元素平方和

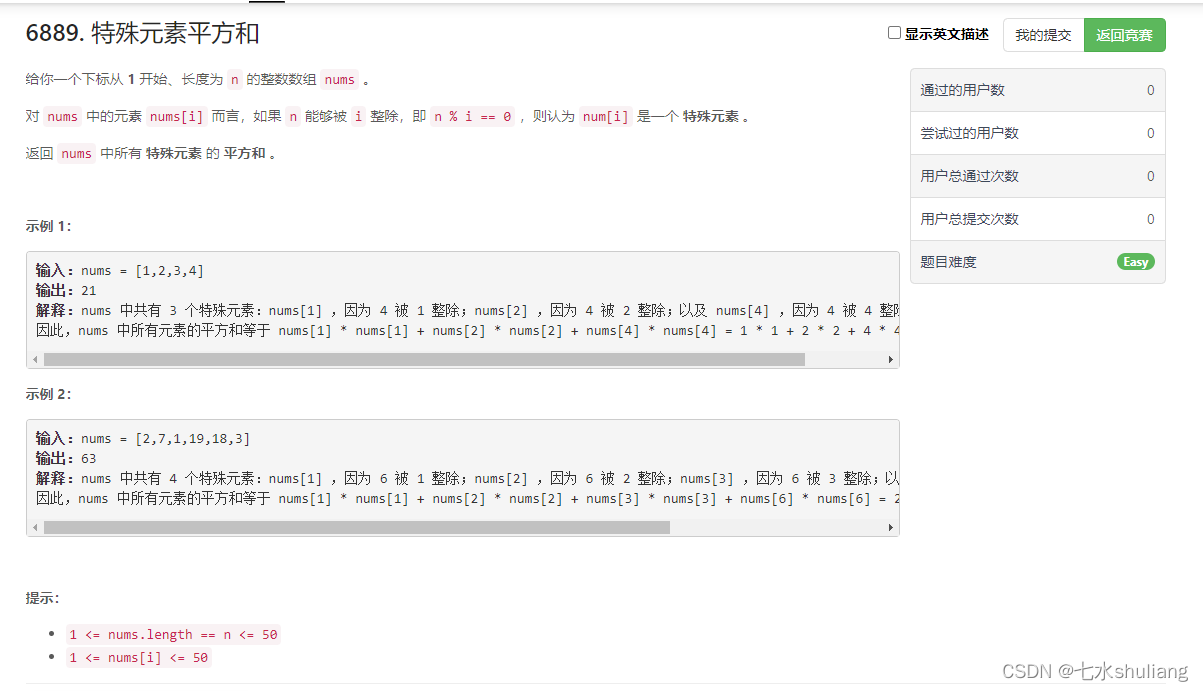
6889. 特殊元素平方和

1. 题目描述

2. 思路分析

按题意模拟即可。

3. 代码实现

class Solution:
    def sumOfSquares(self, nums: List[int]) -> int:
        return sum(v*v for i,v in enumerate(nums,start=1) if len(nums)%i==0)

6929. 数组的最大美丽值

6929. 数组的最大美丽值

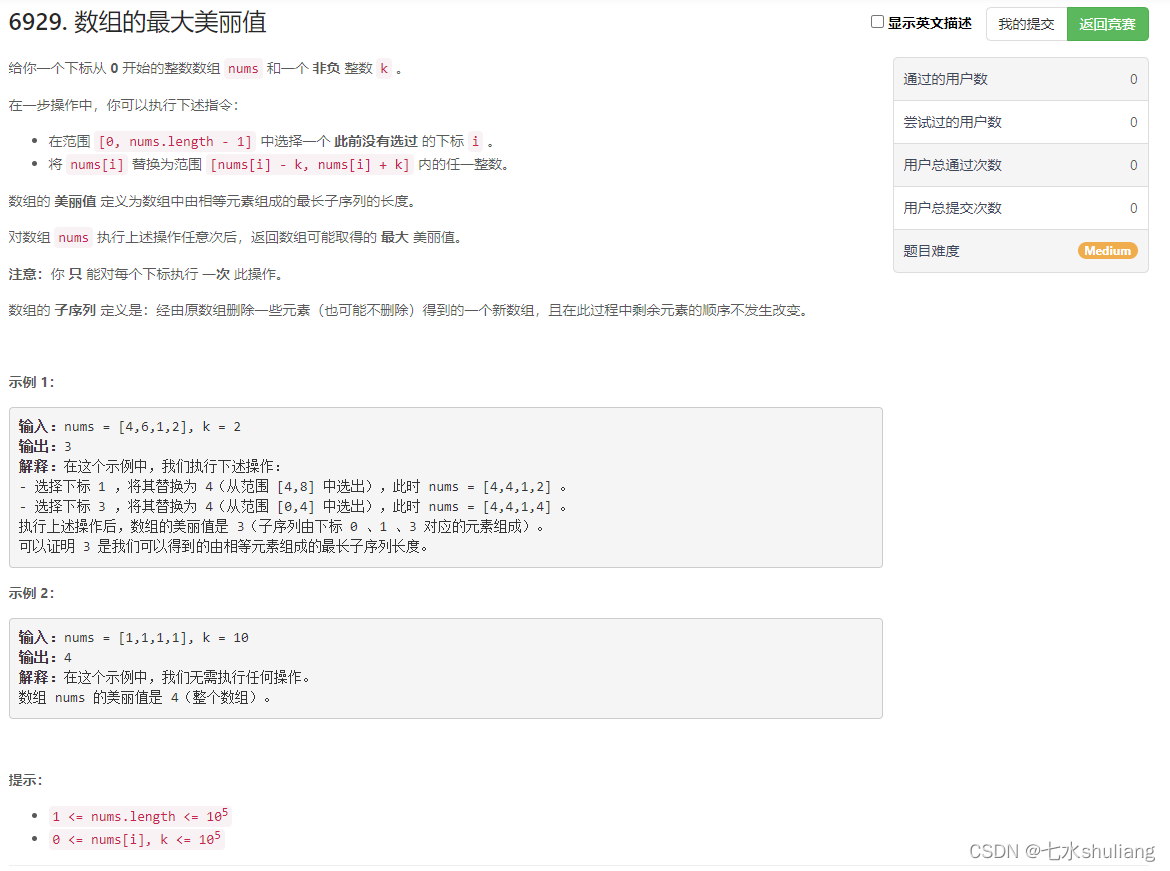
1. 题目描述

2. 思路分析

• 注意到值域很小，因此可以值域当下标，记录每个下标可以被访问多少次。
• 那么其实是个区间+1。用差分可以搞。树状数组也可以。
• 实现时，只需要对值域mn~mx处理即可，因为所有数都加相同的k，边界以外的次数一定不会超过边界（它们一定会路过边界）。

3. 代码实现

class Solution:
    def maximumBeauty(self, nums: List[int], k: int) -> int:
        mx = max(nums)
        d = [0]*(mx+2)
        for v in nums:
            x,y = max(0,v-k), min(mx,v+k)
            d[x] += 1
            d[y+1] -= 1 
            
        return max(accumulate(d))

6927. 合法分割的最小下标

6927. 合法分割的最小下标

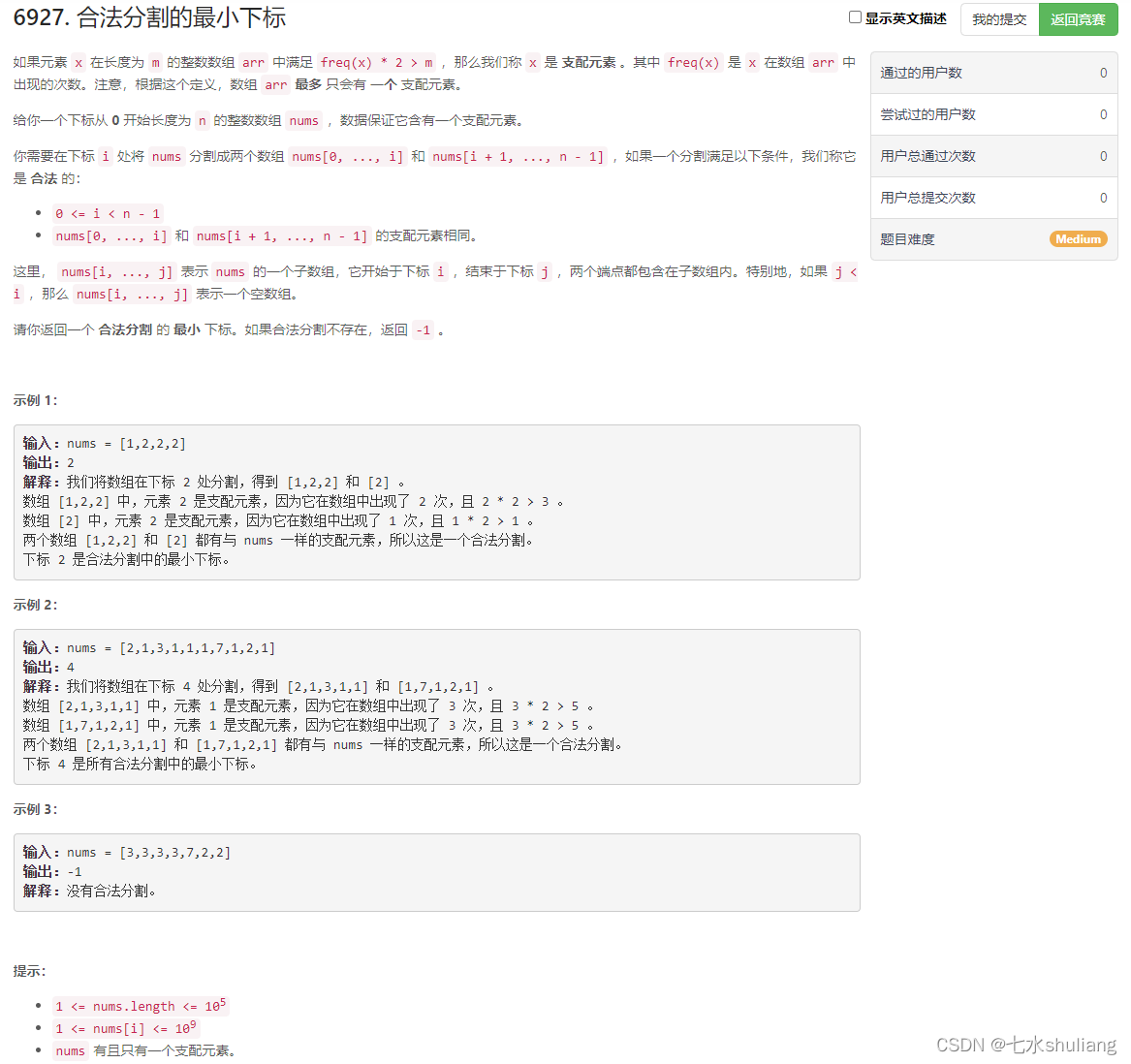
1. 题目描述

2. 思路分析

• 前后缀分解。
• 先计算出主元素x和它出现的次数y。那么前后缀的相同主元素只能是x。
• 那么可以从头向后遍历，记录x的出现次数p，并计算后边剩余的次数y-p。
• 找到第一个满足条件的下标即可。

3. 代码实现

class Solution:
    def minimumIndex(self, nums: List[int]) -> int:
        n = len(nums)
        cnt = Counter(nums)
        x,y = cnt.most_common(1)[0]
        p = 0
        for i,v in enumerate(nums):
            if v == x:
                p += 1 
                if p*2 > i+1 and (y-p)*2>(n-i-1):
                    return i
        return -1

6924. 最长合法子字符串的长度

6924. 最长合法子字符串的长度

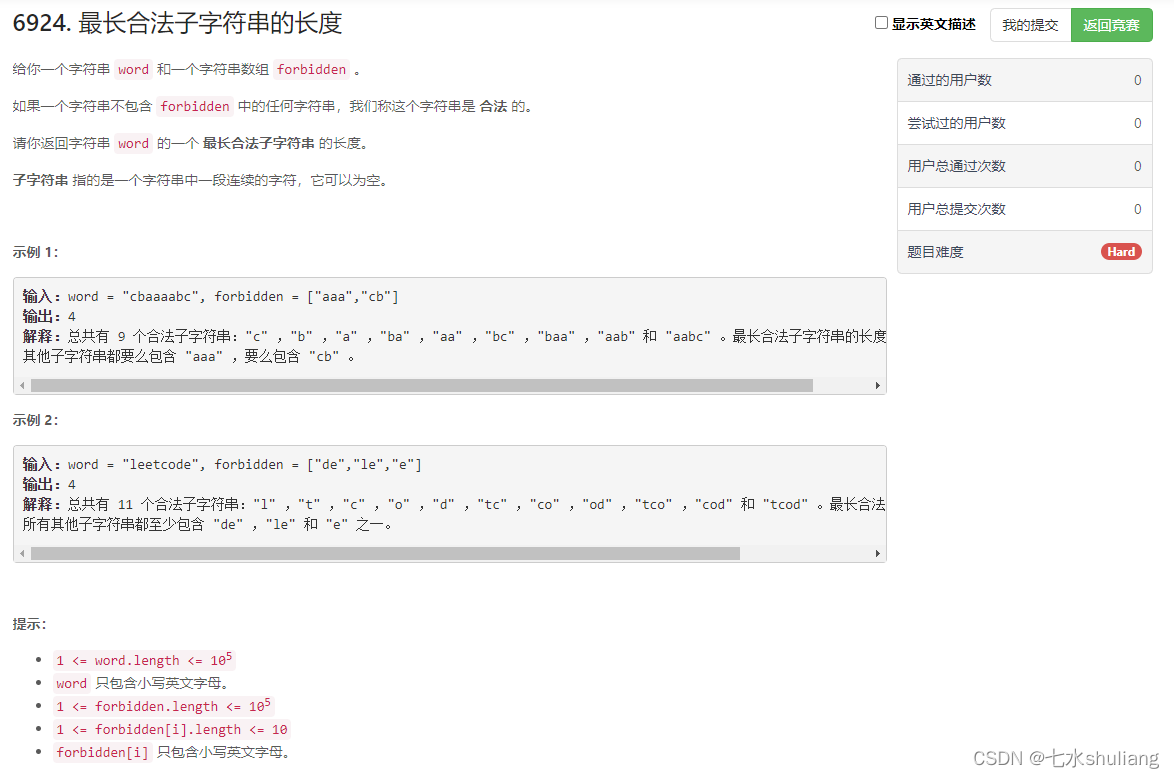
1. 题目描述

2. 思路分析

• 最长子段首先想到双指针/滑窗。
• 枚举每个字母作为子段的右端点。尝试检查这个尾缀里是否再forbid里。
• 由于forbid长度最多10，因此只需要暴力检查10次尾缀，找到最短那个fb尾缀，把左窗口挪过来，注意是l=j+1，因为要破坏这个非法单词。
• 这样复杂度是n1010,每个字符要检查10次，每次检查复杂度是len(s)=10。

---

• 可以用字典树trie优化成n*10。但是实测py果然还是切片+朴素set更快。
• 对forbid逆序建树。
• 枚举c为右端点时，也逆序向前组成字符串，然后去trie里判断是否存在这个单词。
• 由于检查也是从右向左，同步检查，因此复杂度就是10。

3. 代码实现

朴素set

class Solution:
    def longestValidSubstring(self, word: str, forbidden: List[str]) -> int:
        fb = set(forbidden)
        l = ans = 0 
        for r,c in enumerate(word):            
            for j in range(r,max(l-1,r-10),-1):
                if word[j:r+1] in fb:
                    l = j+1
                    break
            # print(r,l)
            ans = max(ans, r-l+1)
        return ans                       

trie

class Solution:
    def longestValidSubstring(self, word: str, forbidden: List[str]) -> int:
        trie = {}
        for s in  forbidden:
            s = s[::-1]
            cur = trie 
            for c in s:
                if c not in cur:
                    cur[c] = {}
                cur = cur[c]
            cur['#'] = 1
        def query(s):
            cur = trie
            for i,c in enumerate(s,start=1):
                if c not in cur:
                    return 0 
                cur = cur[c]
                if '#' in cur:
                    return i 
            return 0
        l = ans = 0 
        for r,c in enumerate(word):     
            s = word[max(l,r-9):r+1] 
            i = query(s[::-1])
            if i:
                l = r - i+2
            ans = max(ans, r-l+1)
        return ans                 

参考链接