目录
1 总结
1.1 本文目标总结方法
1.2 总结一些中间关键函数
2 均值和期望
2.1 求均值的公式
2.2 求随机变量期望的公式
2.3 求随机变量期望的朴素公式
3 方差
3.1 确定数的方差
3.2 统计数的方差公式
3.3 随机变量的方差公式
3.4 EXCEL提供的直接计算方差的公式
4 期望 和方差的公式的实践
4.1 实际计算
4.2 暂时发现,最朴素的期望和方差公式才是通用的,没有之一
5 特殊分布的期望和公式
5.0 用原始的概率,期望和方差的方法
5.0 各种特殊分布的期望和方差公式 (很多对应下面的EXCEL公式)
5.1 超几何分布 HYPGEOM.DIST()
5.2 二项分布 BINOM.DIST()
5.3 泊松分布 poisson.disct()
5.4 几何分布 (暂时没用,可用负二项的)
5.5 负二项分布 negbinom.dist()
5.6 指数分布 expon.dist()
5.7 正态分布 norm.dist()
5.8 其他
1 总结
1.1 本文目标总结方法
- EXCEL用来用计算 期望和方差
- 除了分布计算外,甚至有不少直接求某些期望和方差的公式
- 这里来总结下
1.2 总结一些中间关键函数
- combin() 组合函数
- fact() 阶乘函数
- 排列函数
- 等等
2 均值和期望
2.1 求均值的公式
如果不是随机变量,只能求均值,而均值有很多种,这也对应不同的均值公式
EXCEL都有对应的公式
- 算术平均值,AVERAGE()
- 几何平均值,GEOMEAN()
- 调和平均值,HARMEAN()
- 加权平均值,sumproduct(数列1,数列2)
2.2 求随机变量期望的公式
- 因为随机变量的,数学期望,本质也是一种加权平均值,因为也可以用加权平均值方法求值,sumproduct(数列1,数列2)
- 我现在没发现直接求 随机变量期望的公式
2.3 求随机变量期望的朴素公式
只要是随机变量,不管是哪种特定分布,甚至不知道具体的分布
朴素的期望公式
- E(X)=Σpi*xi
3 方差
3.1 确定数的方差
- D(X) = Σ(xi-均值)^2/n
3.2 统计数的方差公式
- 统计的方差公式 和上面基本相同
- D(X) = Σ(xi-期望)^2/n

3.3 随机变量的方差公式
- 因为是以概率为加权,所以
- D(X) = Σpi*(xi-u)^2
3.4 EXCEL提供的直接计算方差的公式
- 总体方差 VAR.P()
- 样本方差 VAR.S()
- 总体标准差 STDEV.P()
- 样本标准差 STDEV.S()
4 期望 和方差的公式的实践
4.1 实际计算
- 在EXCEL里,朴素的 均值,期望,方差公式,在有限数据的情况下都是可以算的
- 但是EXCEL没有提供通用的,期望和方差的特定计算公式,开始我还觉得奇怪,现在想起来,可能是因为不同的 随机变量,概率分布差别很大,除了统一的朴素 期望公式,朴素方差公式,
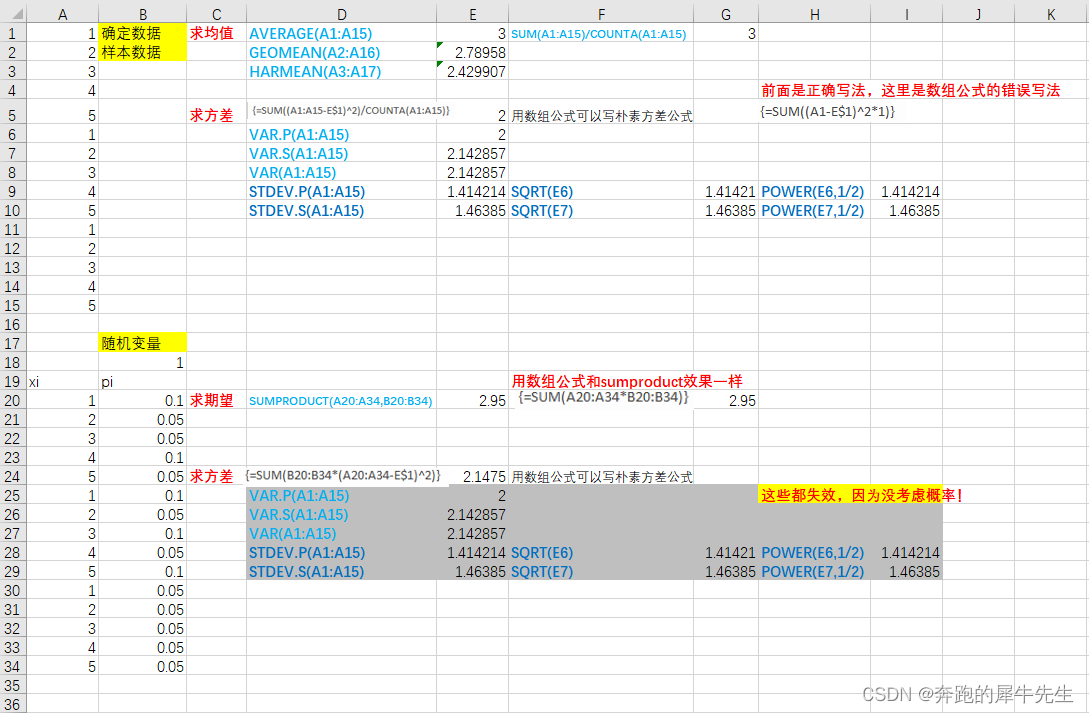
4.2 暂时发现,最朴素的期望和方差公式才是通用的,没有之一
确定数据/样本数据
- 确定数据的期望 E(X) = Σxi/n
- 确定数据的期望 E(X) = Σ(xi-u)^2/n
随机变量的
- 随机变量的期望 E(X) = Σpi*xi
- 随机变量的期望 E(X) = Σpi*(xi-u)^2
5 特殊分布的期望和公式
- 特定的分布,因为期望和方差都有特定公式
- EXCEL单独提供这些分布的期望和方差,直接求得公式
5.0 用原始的概率,期望和方差的方法
- 虽然计算概率,需要用对应分布的公式
- P(x=n) 想了解的随机变量是总次数n,需要对应几何分布,负二项分布
- P(x=k) 想了解的随机变量是成功次数k,需要对应超几何分布部分,二项分布等
- 但是计算,期望和方差可以用,随机变量的朴素的定义公式
- 注意是随机变量的期望和方差朴素定义公式,而不是统计的方差公式等!!
- 比如两种方差公式差别
- 但是也有相同点,可以认为 统计公式里 1/N=p
5.0 各种特殊分布的期望和方差公式 (很多对应下面的EXCEL公式)
- 0-1分布
- 几何分布,P(x=n) = p*(1-p)^n-1, E(x)=1/p , D(x)=(1-p)/p
- 超几何分布,P(x=k) = C(M,k)*C(N-m,n-k)/C(N,n), E(x)=nM/n , D(x)=n*M/N*(1-M/N)*(N-n)/(N-1)
- 二项分布,P(x=k) = C(n,k)*p*(1-p)^n-1, E(x)=np , D(x)=np*(1-p)
- 泊松分布,P(x=k) = λ^*e^-λ/k!, E(x)=λ , D(x)=λ,而λ=np
- 正态分布,
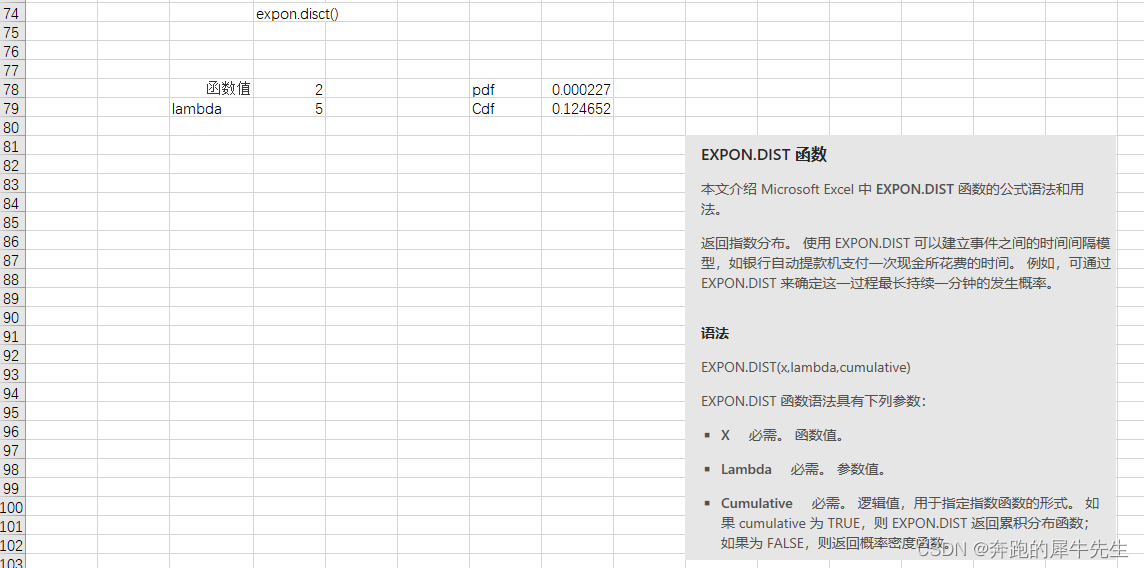
- 指数分布,
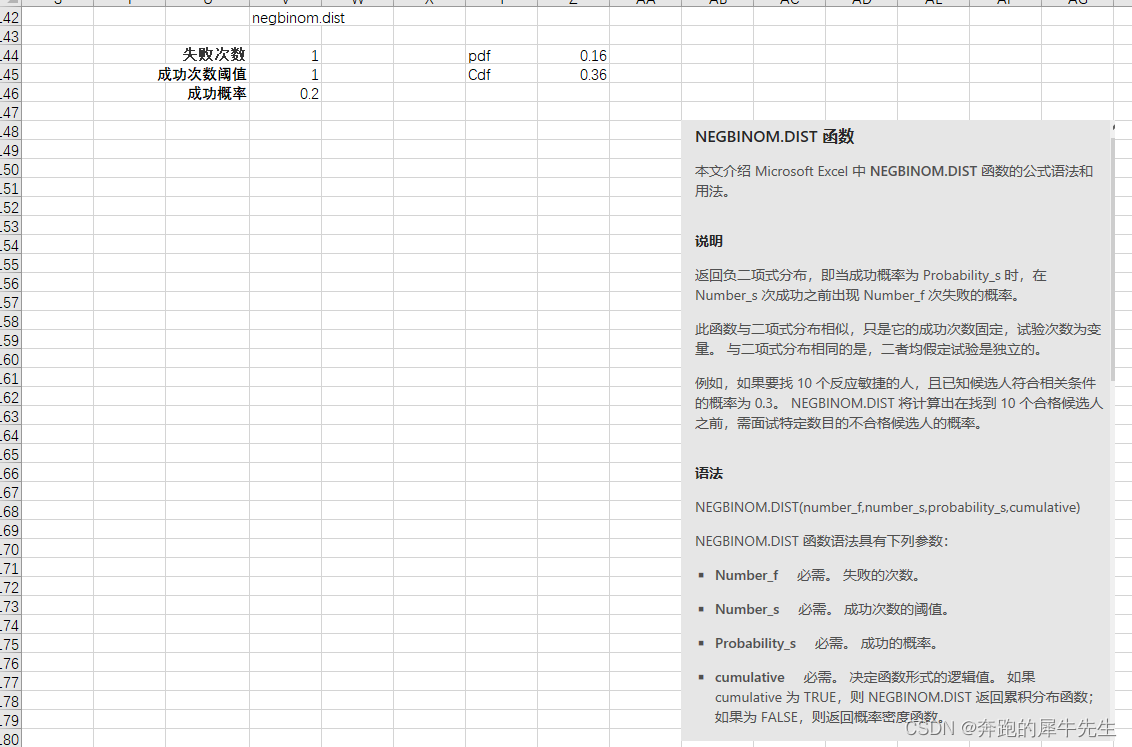
- 负二项分布,
- gamma分布,
5.1 超几何分布 HYPGEOM.DIST()

5.2 二项分布 BINOM.DIST()
- 二项分布可用如下公式
- BINOM.DIST(U3,V$1,V3,FALSE)
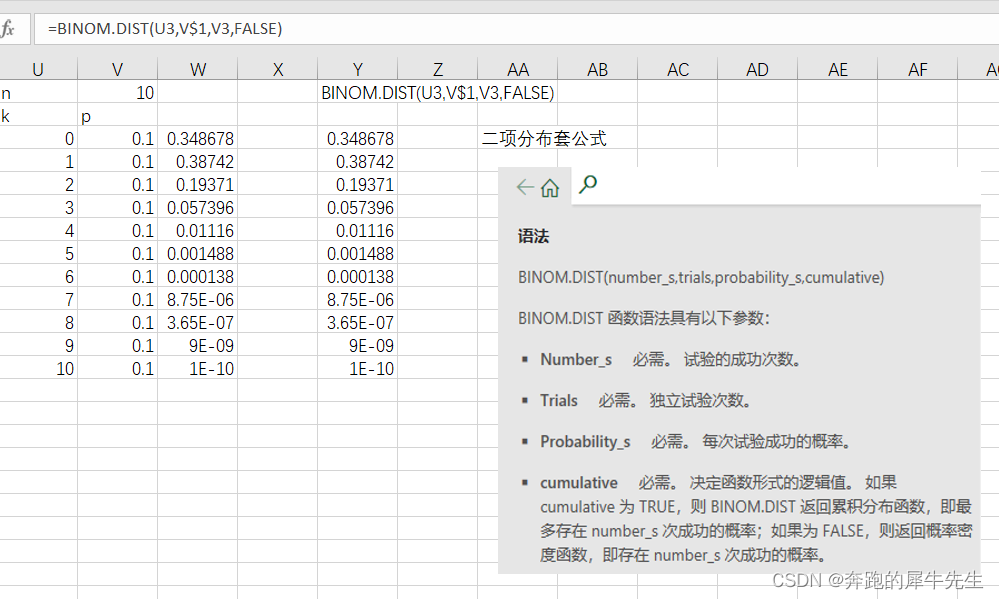
5.3 泊松分布 poisson.disct()
- poisson.disct()
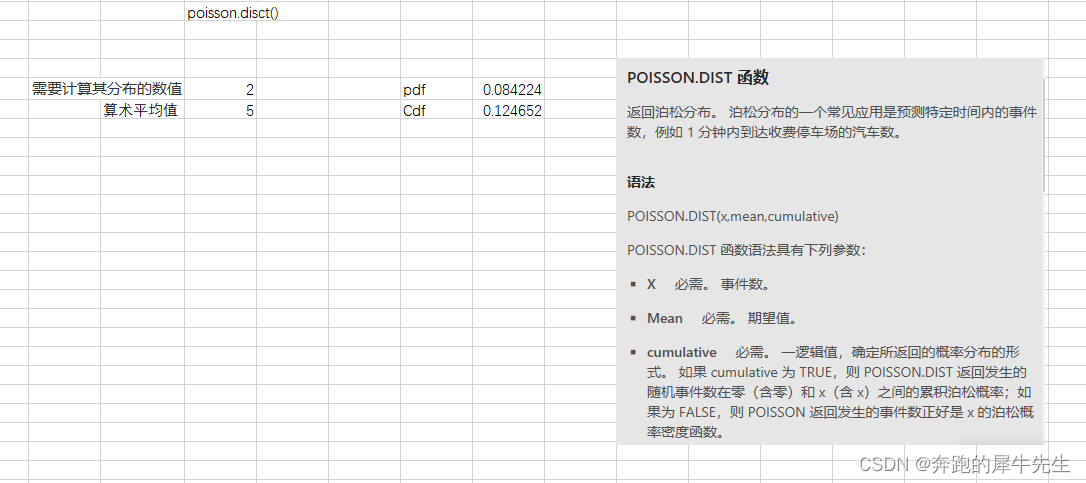
5.4 几何分布 (暂时没用,可用负二项的)
次数=1的特殊,负二项分布
5.5 负二项分布 negbinom.dist()
5.6 指数分布 expon.dist()
- expon.dist()
5.7 正态分布 norm.dist()
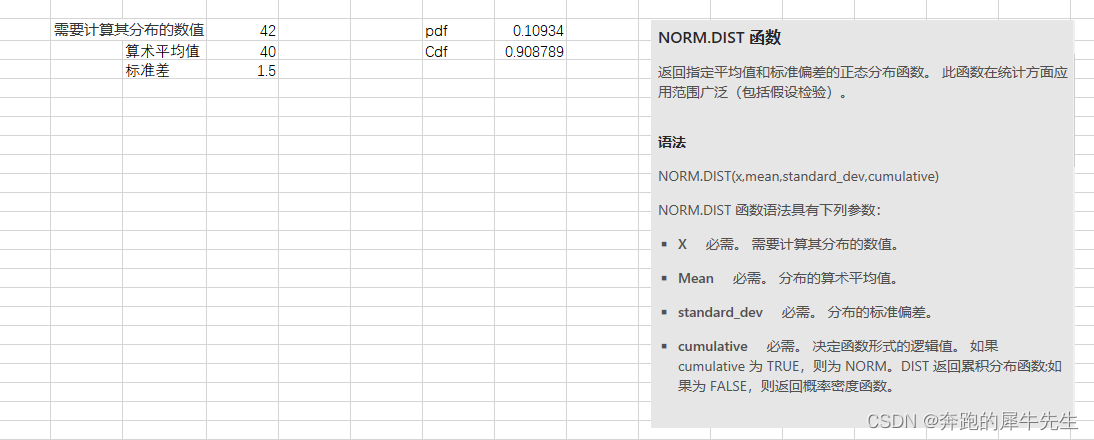
5.8 其他
- fdist F分布