一种用于RBF神经网络的新型自适应内核研究（Matlab代码实现）

news2024/9/22 15:45:31

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

在本文中，我们提出了一种新的径向基函数神经网络自适应核。所提出的核自适应地融合了欧几里得和余弦距离测度，以利用两者的往复性质。该框架使用梯度下降法动态调整参与核的权重，从而减轻了对预定权重的需求。结果表明，所提方法在非线性系统辨识、模式分类和函数逼近3个主要估计问题上优于人工核融合。

RBF 神经网络在许多实际感兴趣的问题上表现出优异的性能。在[24]中，使用具有遗传算法的RBF神经网络分析盐水储层的物理化学特性。所提出的模型称为GA-RBF模型，与以前的方法相比，它显示出良好的结果。在[12]中，RBF核用于高精度地预测压力梯度。在核物理的背景下，RBF已被有效地用于模拟材料的停止功率数据，如[15]。有关各种应用的全面讨论，请参见[6]。

近年来，该领域取得了相当大的进展。在[23]中，提出了几种新的RBF构造算法，目的是用更少的计算节点提高误差收敛率。第一种方法通过添加Nelder-Mead单纯形优化来扩展流行的增量极限学习机算法。第二种算法使用Levenberg-Marquardt算法来优化RBF的位置和高度。与之前的研究相比，结果显示出更好的错误性能。在[19]中，借助模糊聚类和数据预处理技术，开发了优化的RBF神经网络分类器的新架构。在[7]中，一种称为cOptBees的蜜蜂启发算法已被与启发式算法一起使用，以自动选择要在RBF网络中使用的基函数的数量，位置和分散度。由此产生的BeeRBF被证明具有竞争力，并具有自动确定中心数量的优势。为了加速大规模数据序列的学习，[2]提出了一种增量学习算法。模糊聚类和清晰聚类的优点在[18]中得到了有效的结合。

在[5]中，提出了基于正交最小二乘的替代学习过程。在算法中，以合理的方式逐个选择RBF的中心，直到构建出足够的网络。在[10]中，提出了一种具有多核的新型RBF网络，以获得优化且灵活的回归模型。多核的未知中心由改进的 k 均值聚类算法确定。使用正交最小二乘（OLS）算法来确定其余参数。[13]中提出的另一种学习算法通过使用自适应计算算法（ACA）简化了神经网络训练。ACA的收敛性通过李雅普诺夫准则进行分析。在[3]中，提出了一个顺序框架元认知径向基函数网络（McRBFN）及其基于投影的学习（PBL），称为PBL-McRBFN。PBL-McRBFN的灵感来自人类元认知学习原理。该算法基于两个实际问题进行评估，即声发射信号分类和用于癌症分类的乳房X光检查。在[4]中，提出了一种基于神经网络的非参数监督分类器，称为自适应增长神经网络（SAGNN）。SAGNN 允许神经网络根据训练数据调整其大小和结构。评估了该方法的性能以进行故障诊断，并与各种非参数监督神经网络进行了比较。[26]中提出了一种混合优化策略，通过将粒子群优化（PSO）的自适应优化整合到名为HPSOGA的遗传算法（GA）中。该策略用于自动确定径向基函数神经网络的参数（例如，神经元的数量及其各自的中心和半径）。

详细文章讲解见第4部分。

📚2 运行结果

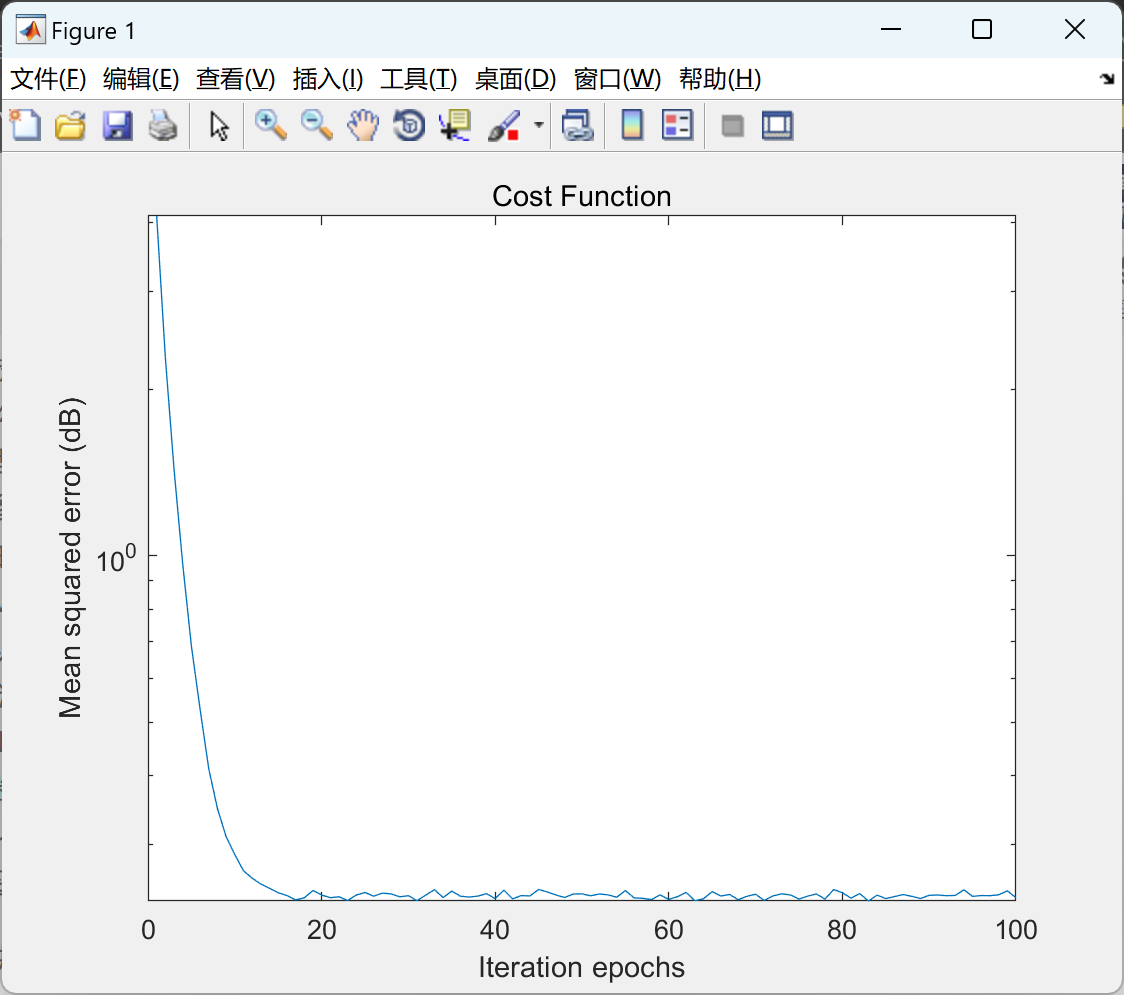
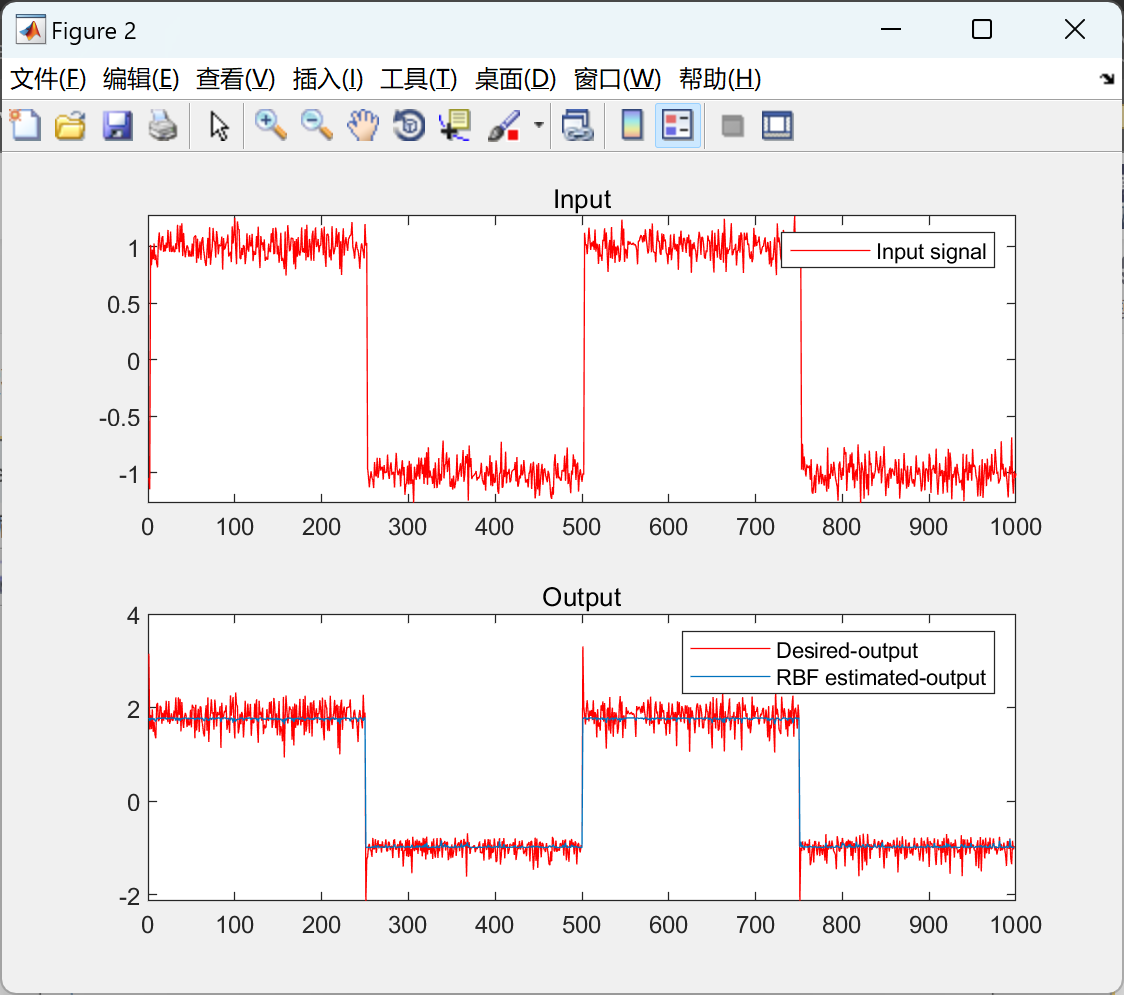
部分代码：

%% Initialization of the simulation parameters
len = 1000; % Length of the signal
runs = 10; % Monte Carlo simulations
epochs = 100; % Number of times same signal pass through the RBF

learning_rate = 5e-4; % step-size of Gradient Descent Algorithm
noise_var=1e-1; % disturbance power / noise in desired outcome

h = [2 -0.5 -0.1 -0.7 3]; % system's coeffients
delays = 2; % order/delay/No.of.Taps

% input signal is a noisy square wave
x=[-1*ones(1,delays) ones(1,round(len/4)) -ones(1,round(len/4)) ones(1,round(len/4)) -ones(1,round(len/4))];
x=awgn(x,20); % addition of noise in square wave signal

c = [-5:2:5]; % Gaussian Kernel's centers
n1=length(c); % Number of neurons
beeta=1; % Spread of Gaussian Kernels
MSE_epoch=0; % Mean square error (MSE) per epoch
MSE_train=0; % MSE after #runs of Monte Carlo simulations

epoch_W1 = 0; % To store final weights after an epoch
epoch_b = 0; % To store final bias after an epoch

%% Training Phase
for run=1:runs
% Random initialization of the RBF weights/bias
W1 = randn(1,n1);
b = randn();

for k=1:epochs

for i1=1:len
% Calculating the kernel matrix
for i2=1:n1
% Euclidean Distance / Gaussian Kernel
ED(i1,i2)=exp((-(norm(x(i1)-c(i2))^2))/beeta^2);
end

% Output of the RBF
y(i1)=W1*ED(i1,:)'+b;

% Desired output + noise/disturbance of measurement
d(i1)= h(1)*x(i1+2) +h(2)*x(i1+1)+h(3)*x(i1)+h(4)*(cos(h(5)*x(i1+2)) +exp(-abs(x(i1+2))))+sqrt(noise_var)*randn();

% Instantaneous error of estimation
e(i1)=d(i1)-y(i1);

% Gradient Descent-based adaptive learning (Training)