题目来源：https://leetcode.cn/problems/jump-game-ii/description/

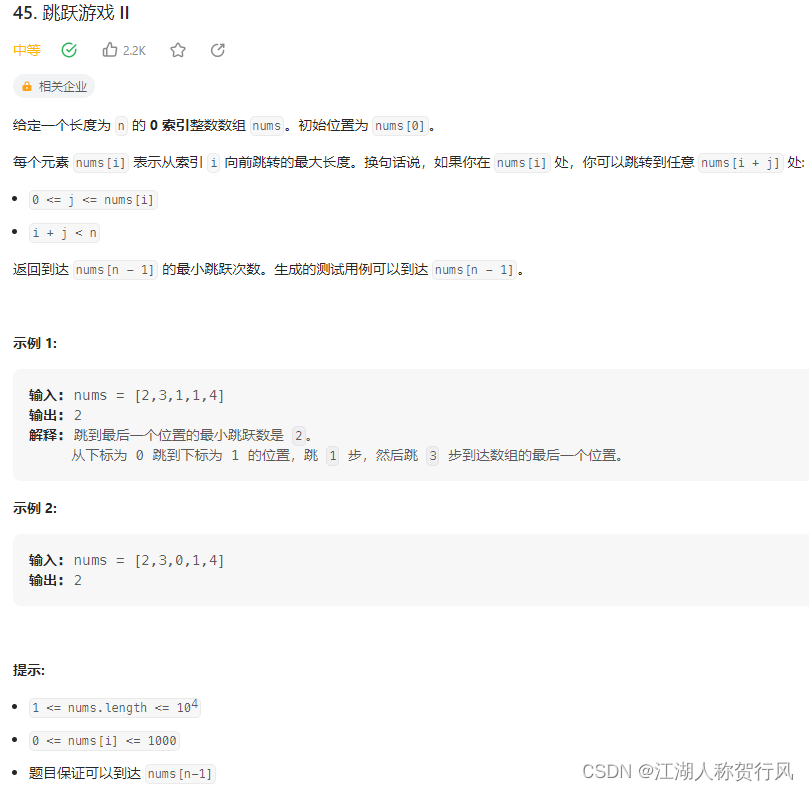
 C++题解1：因为每一步都要能走到下一个更远的地方，就比如 [2,3,1,1,4]，第一步虽然可以到索引2的位置，但是到索引1的位置下一步可以走更远。所以需要记录当前能到的最大范围，也要更新下一步能到的最大范围。确定走下一步时，count要更新。

class Solution {
public:
    int jump(vector<int>& nums) {
        int len = nums.size();
        if(len == 1) return 0;
        int ind = nums[0], nextind = 0;
        int count = 0;
        for(int i = 0; (i < len); i++){
            if(ind >= len-1) {count++; break;}
            int j = i;
            for(; (j <= ind) && (j < len); j++){  // 当前步能走的范围
                nextind = max(nextind, nums[j] + j);  //  更新下一步能走的范围
            }
            i = j - 1;  // 更新下一步的开始落脚点
            ind = nextind; //  更新当前步能走的范围
            count++;  // 确定走下一步
        }
        return count;
    }
};

C++题解2（来源代码随想录）：每一步都更新下一步能走的最大范围，当索引 i 到达当前最大范围，说明需要走下一步，步数加1，当前覆盖最大范围更新。

class Solution {
public:
    int jump(vector<int>& nums) {
        if (nums.size() == 1) return 0;
        int curDistance = 0;    // 当前覆盖最远距离下标
        int ans = 0;            // 记录走的最大步数
        int nextDistance = 0;   // 下一步覆盖最远距离下标
        for (int i = 0; i < nums.size(); i++) {
            nextDistance = max(nums[i] + i, nextDistance);  // 更新下一步覆盖最远距离下标
            if (i == curDistance) {                         // 遇到当前覆盖最远距离下标
                ans++;                                  // 需要走下一步
                curDistance = nextDistance;             // 更新当前覆盖最远距离下标（相当于加油了）
                if (nextDistance >= nums.size() - 1) break;  // 当前覆盖最远距到达集合终点，不用做ans++操作了，直接结束
            }
        }
        return ans;
    }
};

C++题解3（来源代码随想录）：上面的简化版。

class Solution {
public:
    int jump(vector<int>& nums) {
        int curDistance = 0;    // 当前覆盖的最远距离下标
        int ans = 0;            // 记录走的最大步数
        int nextDistance = 0;   // 下一步覆盖的最远距离下标
        for (int i = 0; i < nums.size() - 1; i++) { // 注意这里是小于nums.size() - 1，这是关键所在
            nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖的最远距离下标
            if (i == curDistance) {                 // 遇到当前覆盖的最远距离下标
                curDistance = nextDistance;         // 更新当前覆盖的最远距离下标
                ans++;
            }
        }
        return ans;
    }
};

贪心算法真的又巧又难。。