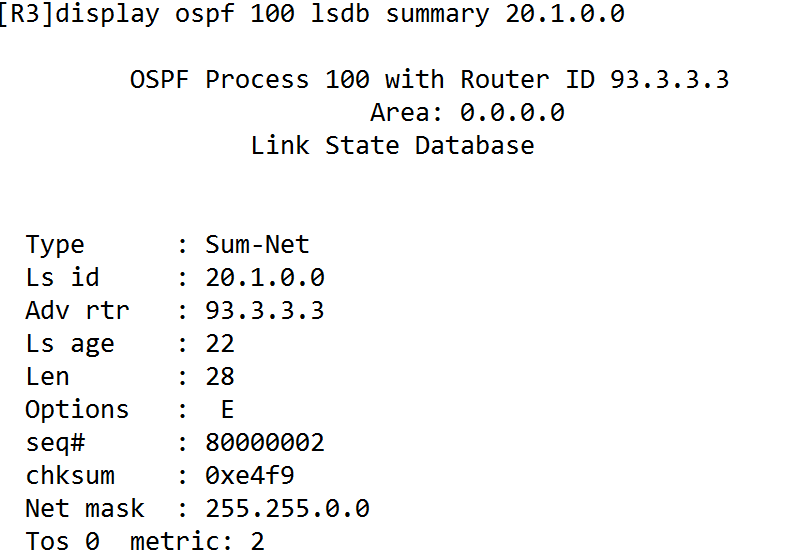
密码学中压缩函数是指将输入的任意长度消息压缩为固定长度输出的函数。压缩函数以两个特定长度的数据为输入，产生与其中一个输入大小相同的输出。简单来说就是它接受一些较长的数据，输出更短的数据。
在CRYPTO 2016，Cogliati和Seurin介绍了Encrypted Davies-Meyer（EDM）结构。
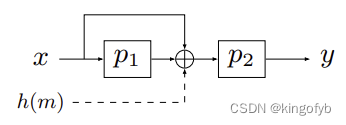
Cogliati和Seurin证明了的行为类似于复杂度为
的随机函数，并实际上推测
是可能的。
构造方法
XOR操作
XOR异或操作是一种按位操作的运算。
XOR的操作对象是2个比特。除两个操作数都是1的情况外，XOR运算与OR运算的结果完全一样。
Davies–Meyer
Davies–Meyer构造方法是是一种很常见的构造压缩函数的方法。压缩函数的第一个和输入块作为分组密码的密钥；第二个输入块作为分组密码的输入进行加密。然后用第二个输入块与分组密码的输出进行异或XOR操作。
使用分组密码F的Davies-Meyer构造的示意图如下所示：
压缩函数的Davies-Meyer构造使用了n位密钥长度和l位块长度的分组密码。
压缩函数可以被定义为：
为了证明所得到的压缩函数的抗碰撞性，我们将F建模为理想密码（理想随机强置换）。任何用于实例化理想密码的分组密码都必须根据理想密码提出的以下更严格的要求进行评估。
- 所有各方都可以访问一个用于随机密钥排列的预言机。
以及它的逆
另一种认为这一点的方法是，每个密钥在l个比特串上指定了一个独立的、一致的置换
(k,·)。 计算
（或
）的唯一方法是用(k，x)显式查询预言机并接收回
(k,x)。
- 理想的密码模型意味着不存在相关的密钥攻击。即，排列
(k,·)和
- 不可能存在一种弱密钥k（例如，全0密钥），因为
- 即使在已知k的情况下，
如果F被建模为理想密码，那么Davies-Meyer构造产生了抗碰撞压缩函数。具体地说，任何对其理想密码预言机进行查询的攻击者都会发现概率最大为
的冲突。
- SHA-2算法的压缩函数采用的就是Davies–Meyer构造方法
