0、二叉树的遍历方式总结

二叉树主要有两种遍历方式
- 深度优先遍历：先往深走，遇到叶子节点再往回走。
- 广度优先遍历：一层一层的去遍历。
从深度优先遍历和广度优先遍历进一步拓展，才有如下遍历方式
- 深度优先遍历
  - 前序遍历（递归法，迭代法）
  - 中序遍历（递归法，迭代法（最好使用统一迭代法））
  - 后序遍历（递归法，迭代法）
- 广度优先遍历
  - 层次遍历（递归法（少见），迭代法）
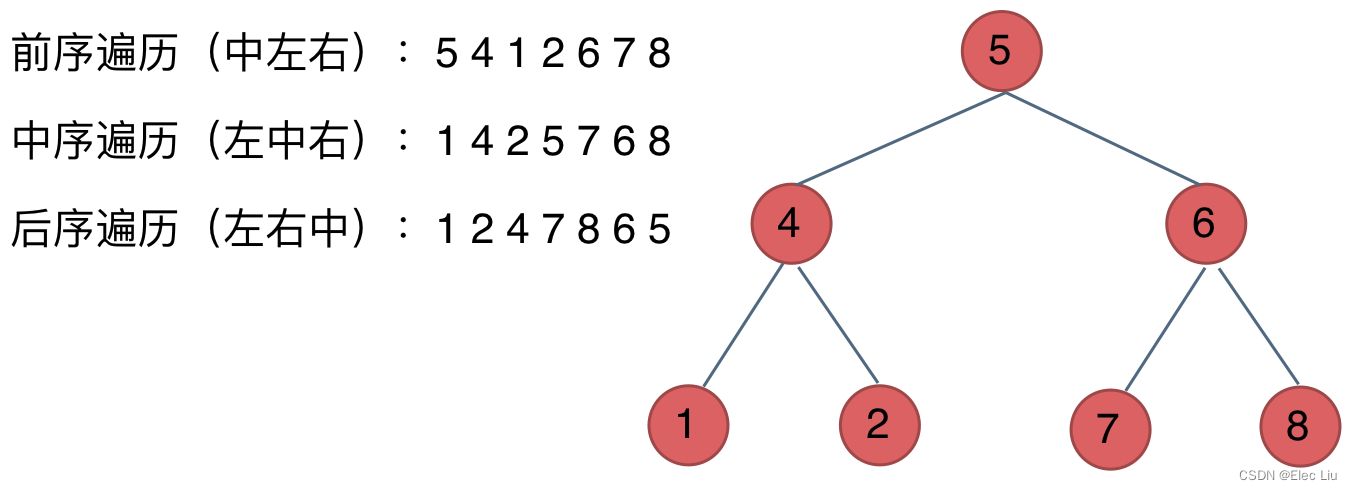
深度优先遍历中的前、中和后指的是中间结点的遍历顺序
其他
- 经常会使用递归的方式来实现深度优先遍历，也就是实现前中后序遍历，使用递归是比较方便的。
- 栈其实就是递归的一种实现结构，也就说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的。
- 广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出的结构，才能一层一层的来遍历二叉树。

1、二叉树的递归遍历

前序递归遍历

class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        vec.push_back(cur->val);    // 中
        traversal(cur->left, vec);  // 左
        traversal(cur->right, vec); // 右
    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};

有了前序遍历，中序遍历和后序遍历只是更换了一下遍历的顺序

中序递归遍历

void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    vec.push_back(cur->val);    // 中
    traversal(cur->right, vec); // 右
}

后序递归遍历

void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    traversal(cur->right, vec); // 右
    vec.push_back(cur->val);    // 中
}

2、二叉树的迭代遍历

前序迭代遍历
前序遍历是中左右，每次先处理的是中间节点，那么先将根节点放入栈中，然后将右孩子加入栈，再加入左孩子。
请添加图片描述

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();                       // 中
            st.pop();
            result.push_back(node->val);
            if (node->right) st.push(node->right);           // 右（空节点不入栈）
            if (node->left) st.push(node->left);             // 左（空节点不入栈）
        }
        return result;
    }
};

后序迭代遍历
先序遍历是中左右，后续遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后再反转result数组，输出的结果顺序就是左右中了，如下图
在这里插入图片描述

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
            if (node->right) st.push(node->right); // 空节点不入栈
        }
        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
        return result;
    }
};

中序迭代遍历
思索一下，中序迭代遍历完全不能用上面的套路，所以如果考到中序的话建议可以使用二叉树的统一迭代法，使用二叉树的统一迭代法是非常方便的。

3、二叉树的统一迭代法

以中序遍历为例，提到说使用栈的话，无法同时解决访问节点（遍历节点）和处理节点（将元素放进结果集）不一致的情况。那我们就将访问的节点放入栈中，把要处理的节点也放入栈中但是要做标记。标记的方法：就是要处理的节点放入栈之后，紧接着放入一个空指针作为标记。这种方法称为标记法

中序统一迭代遍历
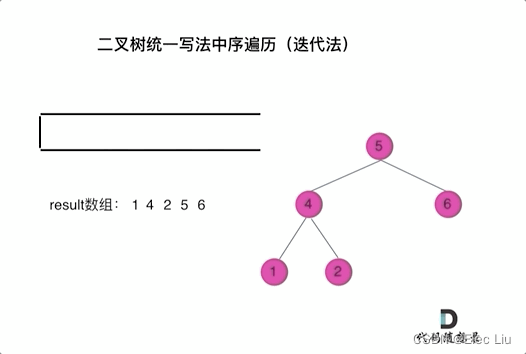
在这里插入图片描述

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                if (node->right) st.push(node->right);  // 添加右节点（空节点不入栈）

                st.push(node);                          // 添加中节点
                st.push(NULL); // 中节点访问过，但是还没有处理，加入空节点做为标记。

                if (node->left) st.push(node->left);    // 添加左节点（空节点不入栈）
            } else { // 只有遇到空节点的时候，才将下一个节点放进结果集
                st.pop();           // 将空节点弹出
                node = st.top();    // 重新取出栈中元素
                st.pop();
                result.push_back(node->val); // 加入到结果集
            }
        }
        return result;
    }
};

有了这份代码，前序代码和后序代码只是修改其中的遍历顺序

前序统一迭代遍历

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
            	...
    	        ...
                st.pop();
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左
                
                st.push(node);                          // 中
                st.push(NULL);
    	        ...
            	...
    }
};

后序统一迭代遍历

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        	    ...
	            ...
                st.pop();
                st.push(node);                          // 中
                st.push(NULL);

                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左
        	    ...
	            ...
    }
};

4、层序遍历

层序遍历需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上

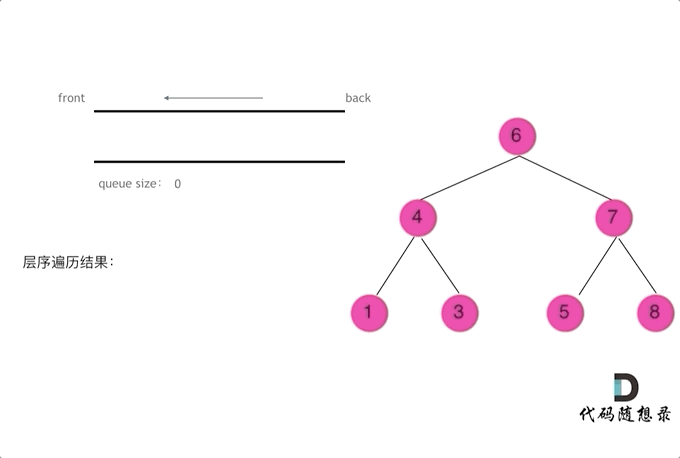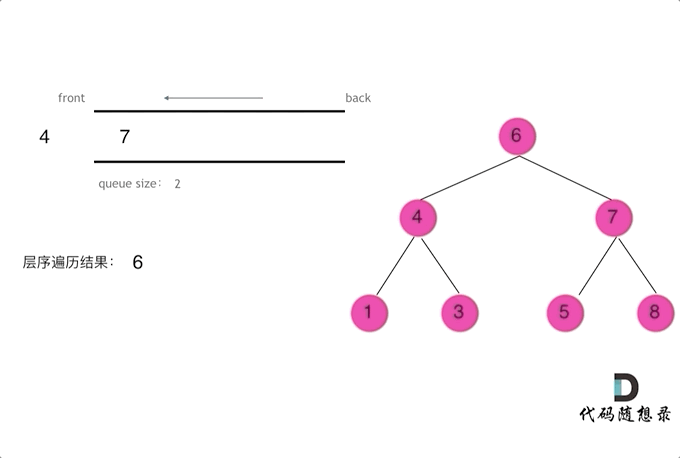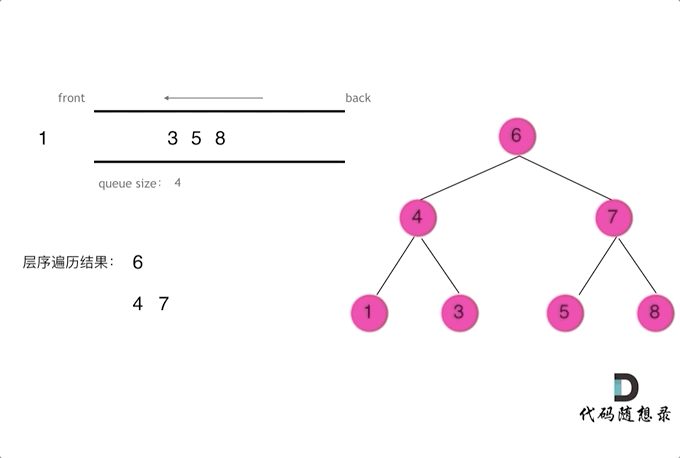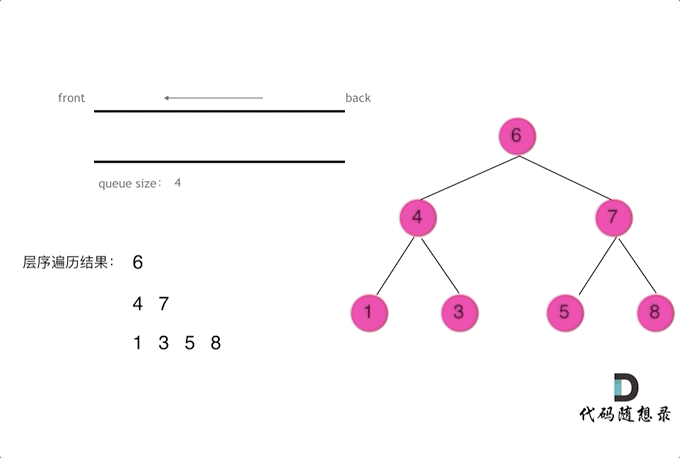
迭代法

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

递归法（这种似乎比较少见）

# 递归法
class Solution {
public:
    void order(TreeNode* cur, vector<vector<int>>& result, int depth)
    {
        if (cur == nullptr) return;
        if (result.size() == depth) result.push_back(vector<int>());
        result[depth].push_back(cur->val);
        order(cur->left, result, depth + 1);
        order(cur->right, result, depth + 1);
    }
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        int depth = 0;
        order(root, result, depth);
        return result;
    }
};