点云表面重建

（1）显式建模方法：
Explicit reconstruction
例如：Delaunay 三角网、Alpha shapes
（2）隐式建模方法：
Implicit reconstruction
例如：径向基函数法、移动最小二乘法、泊松重建法等

Open3d实现的算法：

Alpha shapes
Ball pivoting
Poisson

显示建模

显示建模可以看作一个根据已知的数据采样点，建立几何拓扑关系的过程；

显示建模- Delaunay三角剖分

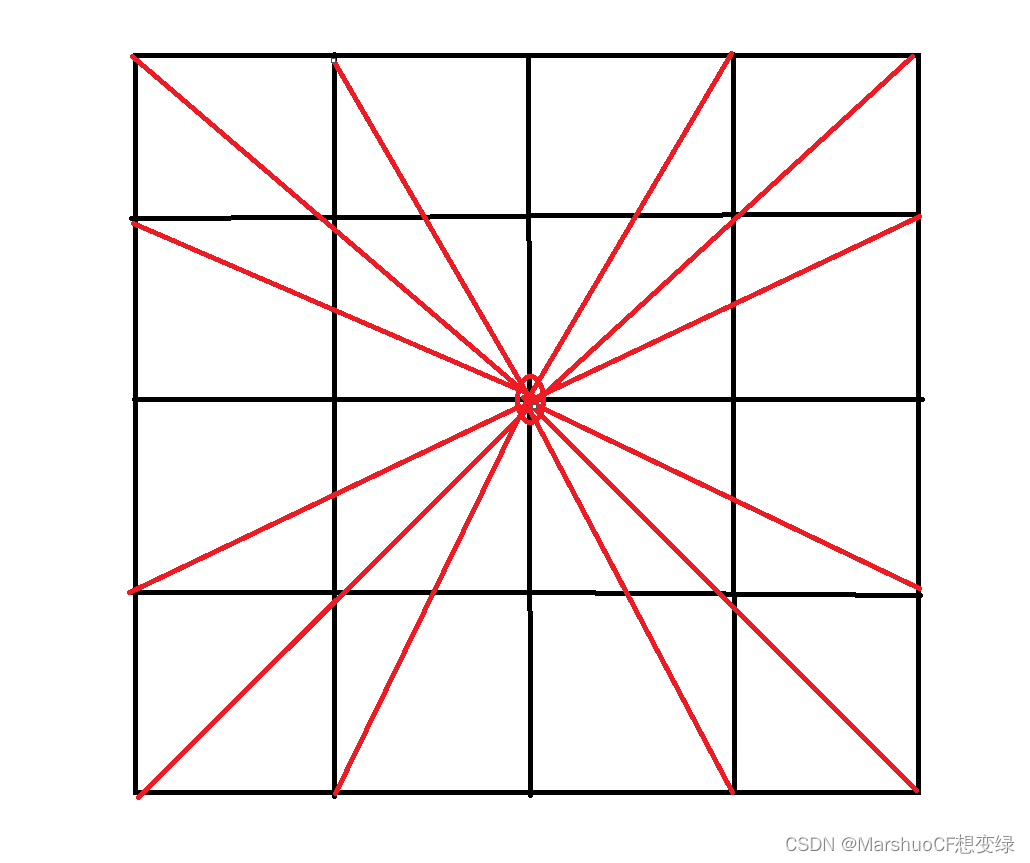
前苏联数学家 Delaunay于1934年提出，对于任意给定的平面点集，该方法遵循“ 最小角最大 ” 和“ 空外接圆 ” 准则进行剖分。
Delaunay 三角网是Voronoi图的伴生图形，通过连接具有公共顶点的三个V n多边形的生长中心而生成的, 这个公共顶点就是形成的Delaunay三角形外接圆的圆心。
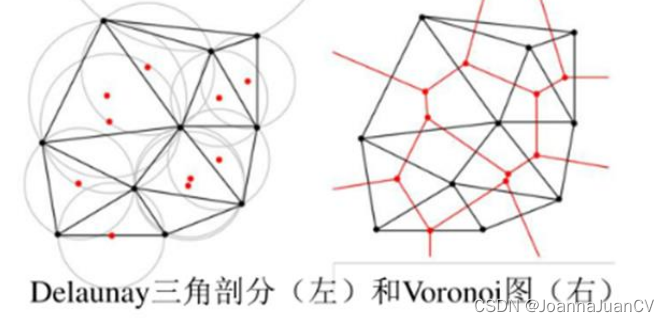
在这里插入图片描述
算法流程：

先将点云通过法线投影到某一二维坐标平面内；
然后对投影得到的点云做平面内的三角化，从而得到各点的拓扑连接关系（基于Delaunay三角剖分）；
最后根据平面内投影点的拓扑连接关系确定各原始三维点间的拓扑连接，所得三角网格即为重建得到的曲面模型；

PCL中的贪婪三角化算法pcl::GreedyProjectionTriangulation使用的是Delaunay三角剖分；

Delaunay三角剖分适用于地貌分析；在这里插入图片描述

显示建模- alpha-shape

计算几何中，alpha shape（α-shape）是描述欧氏平面有限点集形状的一组分段线性简单曲线
算法流程如下：
（1）点云预处理。计算并减去点云质心坐标，将点云移动至坐标轴中心；计算点云特征值和特征向量，对点云做旋转变换（只有2D点云需要做旋转变换）
（2）计算Delaunay三角网。调用qhull库，通过qh_new_qhull函数计算点云在4D空间的凸包
（3）计算每个单纯形的中心。调用qhull库，通过qh_setvoronoi_all函数计算每个单纯形（四面体/三角形）的球心/圆心
（4）确定Alpha Complexes。3D时，遍历土堡中位于下边界（Delaunay三角网）的四面体，计算四面体外接球半径r，若r<α，则保存该四面体的4个三角形边界；若r>=α，则找出四面体中满足要求的三角形并保存。2D时，遍历Delaunay三角网中的三角形，计算三角形外接圆半径r，若r<α，则保存该三角形的3条边，否则跳过（可能单独留下一条边没有什么意义）
（5）确定alpha shape。3D时，遍历Alpha Complexes中所有三角形，若相邻的三角形中有不属于Alpha Complexes的，则为边界三角形，保存下来。2D时，遍历所有边，若相邻边有不属于Alpha Complexes的，则为边界边，保存下来
（6）将点云旋转回来，并加回质心坐标。
在这里插入图片描述
Open3d实现了该算法，接口为create_from_point_cloud_alpha_shape其中包含了一个权重参数 alpha。

import open3d as o3d
mesh = o3d.io.read_triangle_mesh("BunnyMesh.ply")
mesh.compute_vertex_normals()

pcd = mesh.sample_points_poisson_disk(750)
o3d.visualization.draw_geometries([pcd])

# alpha-shape 算法 
alpha = 0.2
mesh = o3d.geometry.TriangleMesh.create_from_point_cloud_alpha_shape(pcd, alpha)
mesh.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh], mesh_show_back_face=True)

在这里插入图片描述
调整权重参数 alpha = 0.01，效果如下图：

调整权重参数 alpha = 0.01，且 pcd = mesh.sample_points_poisson_disk(3000)，效果如下图：

显示建模-Ball Pivoting-滚球法

球旋转算法 (BPA) [Bernardini1999] 是一种与 alpha 形状相关的表面重建方法。直观地，想象一个具有给定半
径的 3D 球，我们将其放在点云上。如果它击中任何 3 个点（并且它没有穿过这 3 个点），它会创建一个三
角形。然后，算法从现有三角形的边缘开始旋转，每次它击中球没有落下的 3 个点时，我们都会创建另一个
三角形。主要思想：想象一个半径为R的球在点云上不停滚动，掠过（不漏下去）的地方建立连接关系形成边、面。
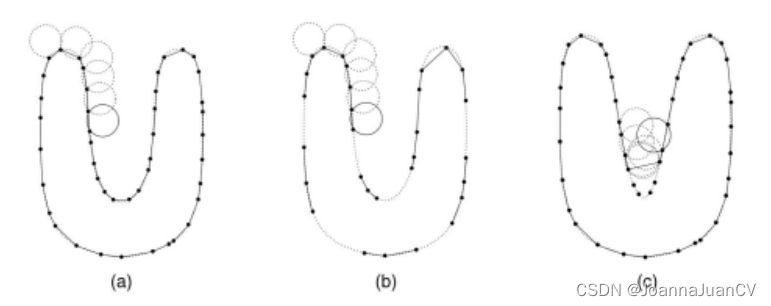
在这里插入图片描述
Open3D 在 create_from_point_cloud_ball_pivoting 中实现了这个方法。该方法接受半径列表作为参数，该参数对应于在点云上旋转的单个球的半径。（该算法假设PointCloud具有法线）

在这里插入代码片

在这里插入图片描述

隐式建模

隐式表面建模对应的是一个插值问题，根据已知的有限的数据采样点，求解连续表面上的未知点的函数值。

隐式建模-Poisson reconstruction-泊松重建

泊松曲面重建方法 [Kazhdan2006] 解决正则化优化问题以获得光滑曲面。出于这个原因，泊松曲面重建可能比上述方法更可取，因为它们会产生不平滑的结果，因为 PointCloud 的点也是生成的三角形网格的顶点，无需任何修改。
核心思想：点云代表了物体表面的位置，其法向量代表了内外的方向。通过隐式地拟合一个由物体派生的指示函数，可以给出一个平滑的物体表面的估计。
Open3D 实现了 create_from_point_cloud_poisson 方法，它基本上是 Kazhdan 代码的包装器。该函数的一个重要参数是深度，它定义了用于表面重建的八叉树的深度，因此意味着生成的三角形网格的分辨率。高的深度值意味着具有更多细节的网格。（该算法假设PointCloud具有法线）

import open3d as o3d
import numpy as np
pcd = o3d.io.read_point_cloud("EaglePointCloud.ply")

print(pcd)
o3d.visualization.draw_geometries([pcd],
                                  zoom=0.664,
                                  front=[-0.4761, -0.4698, -0.7434],
                                  lookat=[1.8900, 3.2596, 0.9284],
                                  up=[0.2304, -0.8825, 0.4101])
# possion
print('run Poisson surface reconstruction')
with o3d.utility.VerbosityContextManager(
        o3d.utility.VerbosityLevel.Debug) as cm:
    mesh, densities = o3d.geometry.TriangleMesh.create_from_point_cloud_poisson(
        pcd, depth=9)
print(mesh)
o3d.visualization.draw_geometries([mesh],
                                  zoom=0.664,
                                  front=[-0.4761, -0.4698, -0.7434],
                                  lookat=[1.8900, 3.2596, 0.9284],
                                  up=[0.2304, -0.8825, 0.4101])

print('remove low density vertices')
# 过滤低密度的点
vertices_to_remove = densities < np.quantile(densities, 0.01)
mesh.remove_vertices_by_mask(vertices_to_remove)
print(mesh)
o3d.visualization.draw_geometries([mesh],
                                  zoom=0.664,
                                  front=[-0.4761, -0.4698, -0.7434],
                                  lookat=[1.8900, 3.2596, 0.9284],
                                  up=[0.2304, -0.8825, 0.4101])