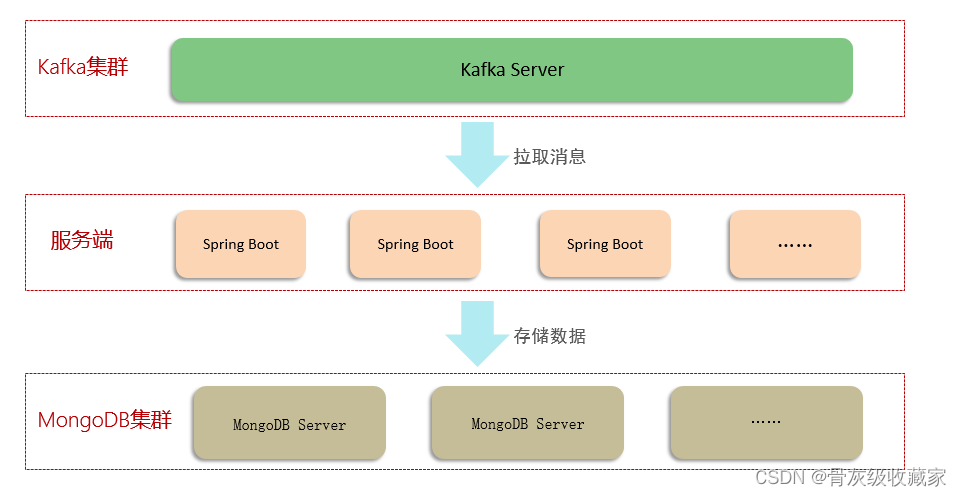
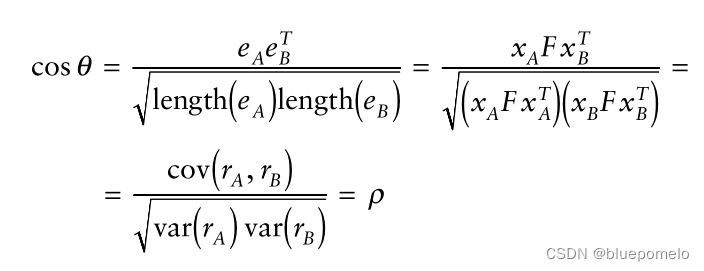我们来看看如何定义距离的计算方法。

回想一下，在共同趋势模型中，协整的必要条件是从共同趋势得到的新息序列必须完全相关。APT中的共同因子回报就理解成是从共同趋势得到的新息序列，因此，新息序列之间的相关系数就是共同因子回报之间的相关系数。那么，这些相关系数越接近1(unity)，两个时间序列越大程度地会协整（comovement)。所以，距离的计算方法设定为：共同因子回报的相关系数的绝对值。犹如以下式子：

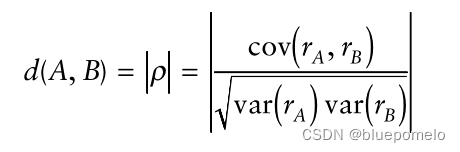
如果用APT的术语来说就是，如果和表示两个股票A和B的因子暴露系数向量，是协方差矩阵，那么距离的计算式子为：

 

 如果两个因子暴露系数向量的夹角越接近0，那么两个时间序列越大程度地协整。但是我们通常不用因子暴露系数向量的夹角去计算，而是用回报的向量夹角，做法是把因子暴露系数空间转换为回报空间再去计算。因为在多因子模型中，因子的地位是不平等的，即回报对不同因子的敏感程度是不一样的。

---

计算两个向量的夹角的cos值

以及是两个向量：

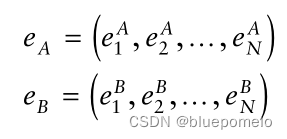
 它们的内积：

 如果使用矩阵的表示方法，则表示为。向量的长度表示为：

 现在我们可以计算两个向量的夹角：

第一步：我们首先计算这两个向量同方向的单位向量（长度为1的向量）。我们通过按这两个向量的长度分别缩放这两个向量的每个元素来实现这一步。

第二步：两个向量之间夹角的余弦现在是跟它们同方先的单位向量的内积。

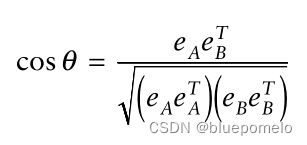
 现在我们看看向量夹角余弦值的几何解释。

协方差矩阵的特征值分解为。和表示两个股票A和B的因子暴露系数向量，那么把这两个向量转换为：

 这就是从因子暴露的空间转换到因子回报空间。

我们继续看：

 两个向量的夹角余弦为：