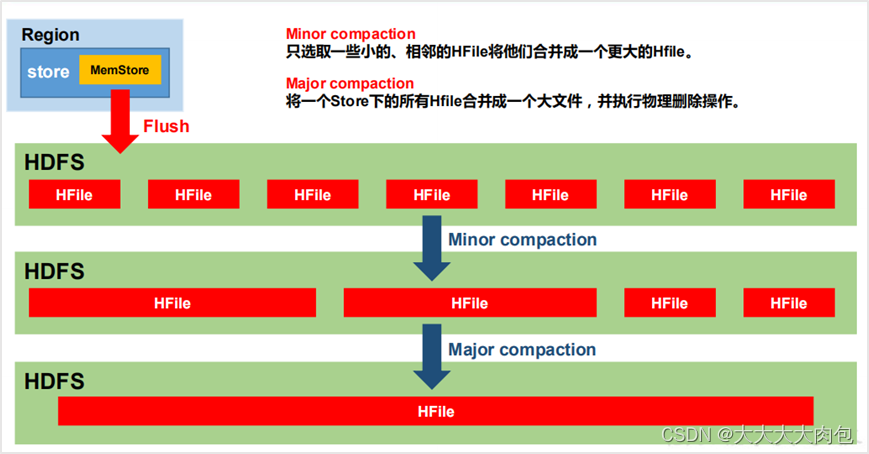
我们有了计算距离的方法,即共同因子相关系数的绝对值就是衡量协整性的一个好方法。现在看一些实际应用中会遇到的问题。
整合的特定回报的平稳性(Stationarity of Integration Specific Returns)
两个时间序列协整的必要条件是整合的特定回报时序是平稳的。我们需要在每个时间周期都评估共同因子以及特定回报的情况。也可以在协整检验阶段去评估。
协整检验包括了估计协整系数,以及保证在这个协整系数下,长短投资组合的价差时序是平稳。如果价差是平稳的,那么就能保证整合的特定回报是平稳的。
偏离最佳条件
以APT的术语来说,两个时间序列协整的话,那么它们的因子暴露系数矩阵的相关系数是+1或者-1。在实际应用中,这是很难达到的条件。如果它们的因子暴露系数矩阵(向量)没有完美的重合,那么由两个股票构成的长短投资组合就会有非零的共同因子回报。然而,协整需要共同因子回报是零值,破坏这个条件就不是完美的协整了。我们看看下面这个式子:

如果是非零的,那么共同因子价差
也是非零值,看下面这个式子,
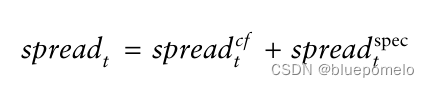
共同因子价差很有可能是非平稳的,破坏了协整的条件即价差是平稳的。
那么如何去衡量这种不完美的协整呢(偏离最佳协整)?我们把价差时序分成两部分,即平稳部分(特定价差)以及非平稳部分(共同因子价差)。用和
代表它们的方差。注意,非平稳部分的方差是跟一个时间范围T绑定在一起的。用
表示交易的时间范围。如果价差的非平稳部分变化很小,那么我们可以把它看作一个常数,然后宣布我们得到了协整的配对。一个衡量偏离最佳协整的方式signal-to-noise是:
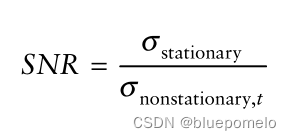
最理想就是非平稳部分(分母)接近0,所以实际应用中,SNR越大说明我们得到的配对越协整。但是随着时间的增加,非平稳部分的方差会越来越大,更短的交易时间范围会更容易得到好的协整配对。(所以这个时间范围要设置多大比较适合?)
回到式子:
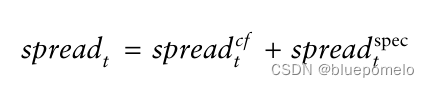
整体价差也可以解释为具有由共同因子价差决定的变化的平均值的特定回报价差。如果共同因子价差是非平稳的时序,那么整体价差就等同于具有随机偏离均值的特定价差。所以,偏离最佳协整条件导致了所谓的均值漂移(mean drift)。
均值漂移的后果是,对称带的交易(trading with symmetric band)可能不是最佳的,因为价差序列的走势可能是偏斜的。更糟糕的是,它可能会根据共同因子价差的移动而向任何方向倾斜,而且不可能提前知道。此外,如果共同因子价差是非平稳的,则偏斜的方差随时间线性缩放。在这个过程中需要注意的是,仅仅时间的流逝就意味着配对交易风险的增加,在设计基于时间的止损单时必须考虑到这一点。
模型误差
当我们的模型设定偏离市场时,就会出现模型误差。比如,有一个戏剧性的消息可能会导致公司基本面发生剧烈变化。市场立即开始对消息进行调整,从某种意义上改变了公司在新情况下的因子敞口(factor exposure)。在这种情况下,因子敞口发生显著变化,之前评估的共同因子相关性将过时,两个股票之间的相关性结构将崩溃。我们要意识到这一点,并在交易配对时不断关注此类事件。
看例子:
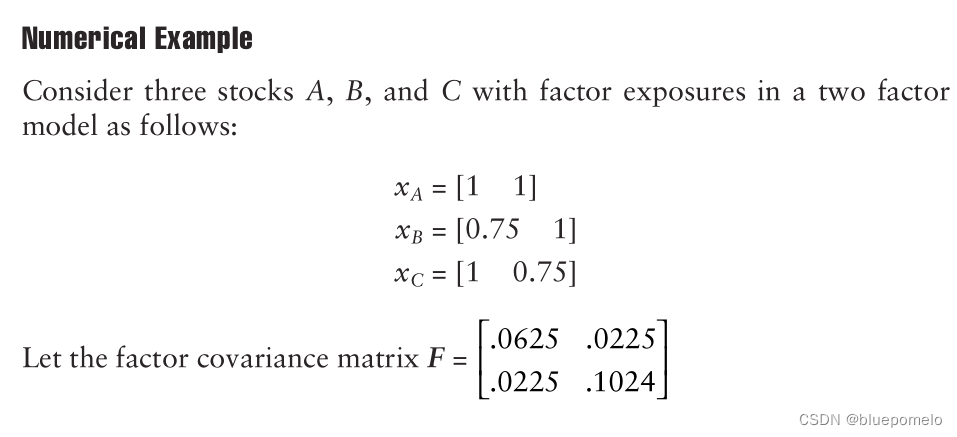








因此,即使在信噪比的基础上,股票对(A,B)也比股票对(A,C)做得更好。注意,具有高的特定风险/方差值(假定它是平稳的)是非常理想的,因为它提高了SNR。较高的特定方差意味着较高的股票波动性,表明高波动性环境有利于配对交易。