前缀和模板算法

news2024/10/6 22:23:19

一)模板前缀和

【模板】前缀和_牛客题霸_牛客网 (nowcoder.com)

前缀和:快速的得出数组中某一段连续区间的和

暴力破解的话需要从头到尾的进行遍历，时间复杂度就可以达到O(N)，而前缀和时间复杂度是可以达到O(1)的

第一步:预处理创建出一个前缀和数组dp，这个数组和原始数组规模是同等大小的

dp[i]就表示从[1,i]区间内所有数组的和

1到N区间内的和和1到L-1区间内的和本质上来说是同一类问题，研究问题的时候发现是同一类问题，我们就可以把这同一类问题抽象成状态表示，用动态规划的思想来进行解决

假设dp[3]表示的就是从1位置到3位置的所有元素的和，就是1+4+7=12

所以状态转移方程就是:dp[i]=dp[i-1]+array[i]；

第二步:使用前缀和数组解决问题:

dp[i]=dp[r]-dp[l-1]

细节问题:在题干中下标为什么从1开始进行计数?

因为如果题目中给定的范围是0-2，那么势必会访问到dp[-1]此时dp表就会出现下标越界访问的情况
public class Main {
    public static void main(String[] args) {
//1.输入数据
        Scanner scanner = new Scanner(System.in);
        int n=scanner.nextInt();
        int count=scanner.nextInt();
         long[] array=new long[n+1];
        for(int i=1;i<=n;i++){
            array[i]=scanner.nextLong();
        }
//2.预处理一个前缀和数组
        long[] dp=new long[n+1];
        for(int i=1;i<=n;i++){
            dp[i]=array[i]+dp[i-1];
        }
//3.使用前缀和数组
        while(count>0){
            count--;
            int left=scanner.nextInt();
            int right=scanner.nextInt();
            System.out.println(dp[right]-dp[left-1]);
        }
    }
}
二)二维前缀和

【模板】二维前缀和_牛客题霸_牛客网 (nowcoder.com)

一)预处理出来一个前缀和矩阵:这个前缀和矩阵必须和原始矩阵规模大小是一样的

dp[i][j]表示从(1，1)这个位置到(i，j)这段区间内，所围成的矩形的，这段区间内所有元素的和

dp[i][j]=dp[i-1][j]+array[i][j]+dp[i][j-1]-dp[i-1][j-1]

result=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]

自己画图可以不花正方形，可以直接画数进行分析
import java.util.Scanner;
import java.util.Arrays;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
//1.先进行处理数据的输入
 Scanner scanner=new Scanner(System.in);
  int m=scanner.nextInt();
  int n=scanner.nextInt();
  int count=scanner.nextInt();//初始化输入次数
  long[][] array=new long[m+1][n+1];
  for(int i=1;i<=m;i++){
    for(int j=1;j<=n;j++){
        array[i][j]=scanner.nextInt();
    }
  }
//2.创建dp表进行填表,使用前缀和数组
long[][] dp=new long[m+1][n+1];
  for(int i=1;i<=m;i++){
    for(int j=1;j<=n;j++){
        dp[i][j]=dp[i-1][j]+array[i][j]+dp[i][j-1]-dp[i-1][j-1];
    }
  }
//2.进行返回结果,使用前缀和数组
   while(count>0){
    int x1=scanner.nextInt();
    int y1=scanner.nextInt();
    int x2=scanner.nextInt();
    int y2=scanner.nextInt();
long result=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1];
// System.out.println(Arrays.deepToString(dp));
  System.out.println(result);
  count--;
}
    }
}

三)寻找数组的中心下标

724. 寻找数组的中心下标 - 力扣（Leetcode）

暴力枚举:每一次枚举一个中间下标i的时候，都需要把(0-i-1)之间的数进行相加，还需要把(i，array.length)之间的数进行相加一遍，可见时间复杂度会变得非常的高

一)定义一个状态表示:

f[i]表示从0号位置到i-1位置，所有元素的和

g[i]表示从i+1号位置到n-1位置，所有元素的和

二)根据状态表示推导状态转移方程

f[i]=f[i-1]+array[i-1]

g[i]=g[i+1]+array[i+1]

三)初始化(防止发生数组越界)

f[0]=0，g[n-1]=0

四)填表顺序:

f表:从左向右

g表:从右向左
class Solution {
    public int pivotIndex(int[] array) {
        int n=array.length;
        int[] f=new int[n];//f[i]表示从0号位置到i位置数组中这段区间内的和
        int[] g=new int[n];//g[i]表示从i+1号位置到n-1位置数组中这段区间的和
        //最后只是需要得出f[i]=g[i]即可
        f[0]=0;//填写到f[0]位置的时候数组就会发生越界
        g[n-1]=0;//因为填写到n-1位置的时候数组就会发生越界
        for(int i=1;i<n;i++){//f从前向后进行填表
            f[i]=f[i-1]+array[i-1];
        }
        for(int i=n-2;i>=0;i--){//g从后向前填表
            g[i]=g[i+1]+array[i+1];
        }
      for(int i=0;i<n;i++){
          if(f[i]==g[i]){
              return i;
          }
      }
      return -1;
    }
}

四)除自身以外数组的乘积:

238. 除自身以外数组的乘积 - 力扣（Leetcode）

一)定义一个状态表示:

f[i]表示从0-i-1位置这段区间所有元素的乘积

g[i]表示从i+1位置开始到n-1这段区间内所有元素的乘积

二)根据状态表示推导状态转移方程:

f[i]=f[i-1]*array[i-1](0号位置的元素到i-2位置的元素的乘积再乘上array[i-1]位置的元素即可)

g[i]=g[i+1]*array[i+1](从i+2号位置的元素到n-1号位置的元素的乘积再乘以i+1号位置的元素)

三)进行初始化操作:f[0]=1，g[n-1]=1

四)填表顺序:f表从左向右填，g表从右向左填
class Solution {
    public int[] productExceptSelf(int[] array) {
//1.创建前缀积以及后缀积数组
        int[] f=new int[array.length];
        int[] g=new int[array.length];
        int[] ret=new int[array.length];
        f[0]=1;
        g[array.length-1]=1;
//2.初始化
        for(int i=1;i<array.length;i++){
            f[i]=f[i-1]*array[i-1];
        }
        for(int i=array.length-2;i>=0;i--){
            g[i]=g[i+1]*array[i+1];
        }
        for(int i=0;i<array.length;i++){
            ret[i]=f[i]*g[i];
        }
     return ret;
    }
}

五)和为K的子数组

剑指 Offer II 010. 和为 k 的子数组 - 力扣（Leetcode）

1)暴力解法:

1)采取枚举策略，定义两个变量i和j，i每次固定不动，j一直向后走，走一步加array[j]，直到遇到sum和等于k

2)但是此时j应该继续向后走，直到j把整个数组遍历完成，因为有可能会出现j遇到整数又遇到负数的情况，此时应该还是让sum=sum+array[j]，如果sum==k，应该再次让count++)，此时的时间复杂度就是O(N^2)

不能使用双指针优化:必须有单调性
class Solution {
    public int subarraySum(int[] array, int k) {
        int count=0;
        for(int i=0;i<array.length;i++){
            int sum=0;
            for(int j=i;j<array.length;j++){
                sum=sum+array[j];
                if(sum==k) count++;
            }
        }
    return count;
    }
}
2)前缀和:

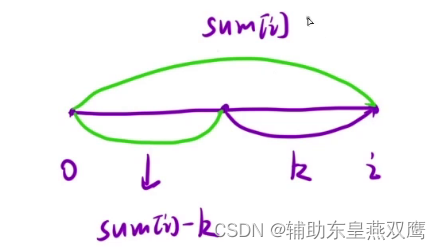
2.1)以i位置为结尾的所有子数组(一定是包含i位置的元素的)，先找到和为K的子数组有多少个，然后把所有情况都进行累加起来

2.2)从而就转化成了在[0~i-1]区间内，i前面有多少个前缀和等于sum[i]-k

如果真的采用上面的思路进行遍历查找(0-i)区间内有多少前缀和等于K，array[right]-array[left-1]=K，那么最终的时间复杂度就是O(N^2)+K，时间复杂度又会飙升
class Solution {
    public int subarraySum(int[] array, int k) {
        //dp[i]表示从0号位置到i号位置所有元素的和,开始初始化dp数组
        int[] dp=new int[array.length+1];
        dp[0]=0;
        for(int i=1;i<=array.length;i++){
            dp[i]=dp[i-1]+array[i-1];
        }
        System.out.println(Arrays.toString(dp));
        int count=0;
        //1.使用前缀和注意下标的映射关系
//2.注意新的dp数组left到right区间内的和有多少等于k是dp[right]-dp[left-1]是[left,right]区间内的和
        for(int left=1;left<=array.length;left++){
            for(int right=left;right<=array.length;right++){
                if(dp[right]-dp[left-1]==k) count++;
            }
        }
        return count;
    }
}