将 n 堆石子绕圆形操场排放，现要将石子有序地合并成一堆。

规定每次只能选相邻的两堆合并成新的一堆，并将新的一堆的石子数记做该次合并的得分。

请编写一个程序，读入堆数 nn 及每堆的石子数，并进行如下计算：

• 选择一种合并石子的方案，使得做 n−1 次合并得分总和最大。
• 选择一种合并石子的方案，使得做 n−1 次合并得分总和最小。

输入格式

第一行包含整数 n，表示共有 n 堆石子。

第二行包含 n 个整数，分别表示每堆石子的数量。

输出格式

输出共两行：

第一行为合并得分总和最小值，

第二行为合并得分总和最大值。

数据范围

1≤n≤200

输入样例：

4
4 5 9 4

输出样例：

43
54

思路：

区间DP

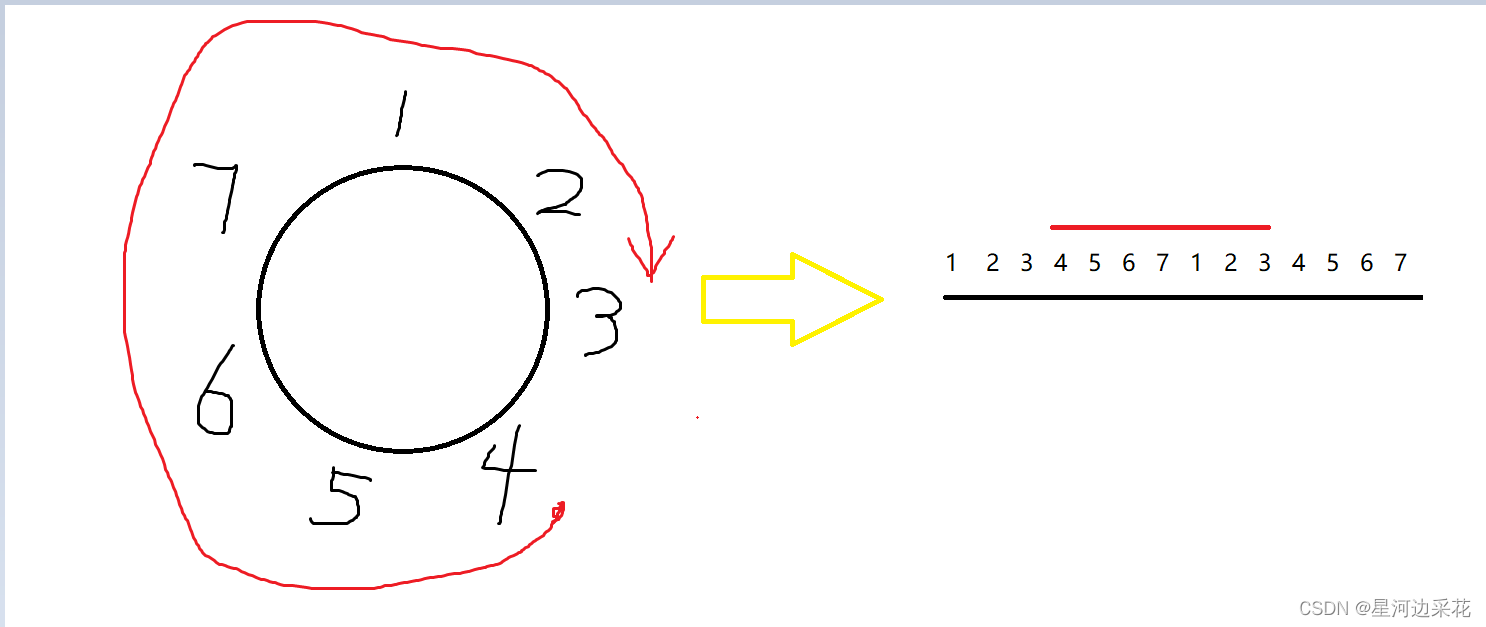
将石子环形摆放，我们要将它变成链式，用到一个常用技巧

将原边长度变为两倍，枚举每一个起点和长度就可以了

 

代码（有注释）：

#include <bits/stdc++.h>
#define LL long long
using namespace std;
//N要开两倍大
const int N = 410,INF=0x3f3f3f3f;
int n;
//w权值数组，s前缀和数组
int w[N], s[N];
//f存最小，g存最大
int f[N][N], g[N][N];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> w[i];
        w[i + n] = w[i];
    }
    //求前缀和
    for (int i = 1; i <= 2 * n; i++)s[i] = s[i - 1] + w[i];

    memset(f, 0x3f, sizeof f);
    memset(g, -0x3f, sizeof g);
    //r-l+1 = len
    //r = l+len-1
    //r <= 2*n
    for (int len = 1; len <= n; len++) {//遍历长度
        for (int l = 1; l + len - 1 <= 2 * n; l++) {//遍历起点
            int r = l + len - 1;

            if (l == r)f[l][r] = g[l][r] = 0;
            else {
                for (int k = l; k < r; k++) {//遍历分界点
                    f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
                    g[l][r] = max(g[l][r], g[l][k] + g[k + 1][r] + s[r] - s[l - 1]);
                }
            }
            
        }
    }

    int maxv = -INF, minv = INF;
    for (int i = 1; i <= n; i++) {
        minv = min(minv, f[i][i + n - 1]);
        maxv = max(maxv, g[i][i + n - 1]);
    }
    cout << minv << endl << maxv;
    return 0;
}