代码随想录刷题记录day39 完全背包+零钱兑换 II+组合总和 Ⅳ

参考：代码随想录

完全背包

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

和0 1背包的区别就是物品加入的次数，完全背包物品可以加入无限次。

所以遍历顺序需要改变。要从小到大去遍历物品。

// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

遍历顺序是可以颠倒的。

518. 零钱兑换 II

思想

完全背包问题，集合中的数可以重复放入背包种

设计到遍历顺序

先遍历物品，再遍历背包，是组合顺序

       for(int i=0;i<coins.length;i++){//遍历背包
            for(int j=coins[i];j<=amount;j++){//遍历物品
                dp[j]+=dp[j-coins[i]];
                System.out.println("i:"+i+",j:"+j+",dp[j]:"+dp[j]);
            }
            System.out.println("\b");
        }

打印数组如下：

i:0,j:1dp[j]:1
i:0,j:2dp[j]:1
i:0,j:3dp[j]:1
i:0,j:4dp[j]:1
i:0,j:5dp[j]:1

i:1,j:2dp[j]:2
i:1,j:3dp[j]:2
i:1,j:4dp[j]:3
i:1,j:5dp[j]:3

i:2,j:5dp[j]:4

先遍历背包在遍历物品，是排列顺序

for(int j=0;j<=amount;j++ ){//遍历背包
    for(int i=0;i<coins.length;i++){//遍历物品
        if (j>=coins[i])dp[j]+=dp[j-coins[i]];
        System.out.println("i:"+i+",j:"+j+",dp[j]:"+dp[j]);
    }
    System.out.println("\b");
}

打印数组如下：

i:0,j:0,dp[j]:1
i:1,j:0,dp[j]:1
i:2,j:0,dp[j]:1

i:0,j:1,dp[j]:1
i:1,j:1,dp[j]:1
i:2,j:1,dp[j]:1

i:0,j:2,dp[j]:1
i:1,j:2,dp[j]:2
i:2,j:2,dp[j]:2

i:0,j:3,dp[j]:2
i:1,j:3,dp[j]:3
i:2,j:3,dp[j]:3

i:0,j:4,dp[j]:3
i:1,j:4,dp[j]:5
i:2,j:4,dp[j]:5

i:0,j:5,dp[j]:5
i:1,j:5,dp[j]:8
i:2,j:5,dp[j]:9

代码

public int change(int amount, int[] coins) {

        //dp[j]表示容量为j的背包，有dp[j]种方法。

        //dp[j]+=dp[j-coins[i]]
        int[] dp=new int[amount+1];
        dp[0]=1;

        //递推公式
        //假设背包的容量，j=5，
        // 如果有一个重量1，有dp[4]种方法可以装满背包
        //如果有一个重量2，有dp[3]种方法可以装满背包
        //如果有一个重量3，有dp[2]种方法可以装满背包
        //如果有一个重量4，有dp[1]种方法可以装满背包
        //如果有一个重量5，有dp[0]种方法可以装满背包
        //dp[j]+=dp[j-coins[i]]

        for(int i=0;i<coins.length;i++){//遍历物品
            for(int j=coins[i];j<=amount;j++){//遍历背包
                dp[j]+=dp[j-coins[i]];
                System.out.println("i:"+i+",j:"+j+",dp[j]:"+dp[j]);
            }
            System.out.println("\b");
        }

//        for(int j=0;j<=amount;j++ ){//遍历背包
//            for(int i=0;i<coins.length;i++){//遍历物品
//                if (j>=coins[i])dp[j]+=dp[j-coins[i]];
//                System.out.println("i:"+i+",j:"+j+",dp[j]:"+dp[j]);
//            }
//            System.out.println("\b");
//        }

        return dp[amount];

    }

377. 组合总和 Ⅳ

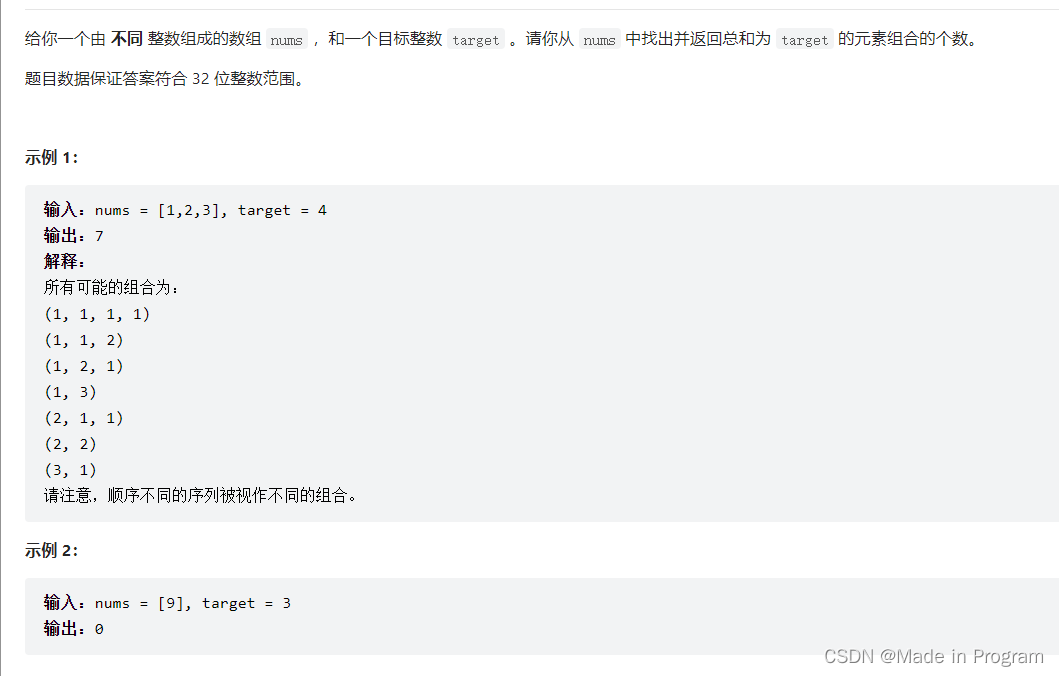
思想

就是上一题提到的排列的情况。

但是还没有完全理解呀！！！

动态规划好难~

代码

class Solution {
    public int combinationSum4(int[] nums, int target) {
        //dp[j] 表示容量为j的背包可以 装满有dp[j]种

        int [] dp=new int[target+1];
        dp[0]=1;

        // for(int i=0;i<nums.length;i++){
        //     for(int j=nums[i];j<=target;j++){
        //         dp[j]+=dp[j-nums[i]];
        //         System.out.println(dp[j]);
        //     }
        // }

        for(int j=0;j<=target;j++){
            for(int i=0;i<nums.length;i++){
                if(j>=nums[i])dp[j]+=dp[j-nums[i]];
            }
        }
        return dp[target];

    }
}