文章和代码已经归档至【Github仓库:https://github.com/timerring/dive-into-AI 】或者公众号【AIShareLab】回复 pytorch教程 也可获取。
文章目录
- nn网络层-池化-线性-激活函数层
- 池化层
- 最大池化:nn.MaxPool2d()
- nn.AvgPool2d()
- nn.MaxUnpool2d()
- 线性层
- 激活函数层
- nn.Sigmoid
- nn.tanh
- nn.ReLU(修正线性单元)
- nn.LeakyReLU
- nn.PReLU
- nn.RReLU
nn网络层-池化-线性-激活函数层
池化层
池化的作用则体现在降采样:保留显著特征、降低特征维度,增大 kernel 的感受面。 另外一点值得注意:pooling 也可以提供一些旋转不变性。 池化层可对提取到的特征信息进行降维,一方面使特征图变小,简化网络计算复杂度并在一定程度上避免过拟合的出现;一方面进行特征压缩,提取主要特征。
池化可以实现一个冗余信息的剔除,以及减少后面的计算量。
最大池化:nn.MaxPool2d()
nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
这个函数的功能是进行 2 维的最大池化,主要参数如下:
- kernel_size:池化核尺寸
- stride:步长,通常与 kernel_size 一致
- padding:填充宽度,主要是为了调整输出的特征图大小,一般把 padding 设置合适的值后,保持输入和输出的图像尺寸不变。
- dilation:池化间隔大小,默认为 1。常用于图像分割任务中,主要是为了提升感受野
- ceil_mode:默认为 False,尺寸向下取整。为 True 时,尺寸向上取整
- return_indices:为 True 时,返回最大池化所使用的像素的索引,这些记录的索引通常在反最大池化时使用,把小的特征图反池化到大的特征图时,每一个像素放在哪个位置。
下图 (a) 表示反池化,(b) 表示上采样,© 表示反卷积。

平均池化与最大池化的差距一般体现在图像的整体亮度上。由于最大池化取得是最大值,因此在亮度上一般是大于平均池化结果的。
下面是最大池化的代码:
import os
import torch
import torch.nn as nn
from torchvision import transforms
from matplotlib import pyplot as plt
from PIL import Image
from common_tools import transform_invert, set_seed
set_seed(1) # 设置随机种子
# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "imgs/lena.png")
img = Image.open(path_img).convert('RGB') # 0~255
# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0) # C*H*W to B*C*H*W
# ================================= create convolution layer ==================================
# ================ maxpool
flag = 1
# flag = 0
if flag:
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2)) # input:(i, o, size) weights:(o, i , h, w)
img_pool = maxpool_layer(img_tensor)
print("池化前尺寸:{}\n池化后尺寸:{}".format(img_tensor.shape, img_pool.shape))
img_pool = transform_invert(img_pool[0, 0:3, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_pool)
plt.subplot(121).imshow(img_raw)
plt.show()
结果和展示的图片如下:
池化前尺寸:torch.Size([1, 3, 512, 512])
池化后尺寸:torch.Size([1, 3, 256, 256])
nn.AvgPool2d()
torch.nn.AvgPool2d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True, divisor_override=None)
这个函数的功能是进行 2 维的平均池化,主要参数如下:
- kernel_size:池化核尺寸
- stride:步长,通常与 kernel_size 一致
- padding:填充宽度,主要是为了调整输出的特征图大小,一般把 padding 设置合适的值后,保持输入和输出的图像尺寸不变。
- dilation:池化间隔大小,默认为 1。常用于图像分割任务中,主要是为了提升感受野
- ceil_mode:默认为 False,尺寸向下取整。为 True 时,尺寸向上取整
- count_include_pad:在计算平均值时,是否把填充值考虑在内计算
- divisor_override:除法因子。在计算平均值时,分子是像素值的总和,分母默认是像素值的个数。如果设置了 divisor_override,把分母改为 divisor_override。
img_tensor = torch.ones((1, 1, 4, 4))
avgpool_layer = nn.AvgPool2d((2, 2), stride=(2, 2))
img_pool = avgpool_layer(img_tensor)
print("raw_img:\n{}\npooling_img:\n{}".format(img_tensor, img_pool))
输出如下:
raw_img:
tensor([[[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]]])
pooling_img:
tensor([[[[1., 1.],
[1., 1.]]]])
加上divisor_override=3后,输出如下:
raw_img:
tensor([[[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]]])
pooling_img:
tensor([[[[1.3333, 1.3333],
[1.3333, 1.3333]]]])
nn.MaxUnpool2d()
nn.MaxUnpool2d(kernel_size, stride=None, padding=0)
功能是对二维信号(图像)进行最大值反池化,主要参数如下:
- kernel_size:池化核尺寸
- stride:步长,通常与 kernel_size 一致
- padding:填充宽度
代码如下:
# pooling
img_tensor = torch.randint(high=5, size=(1, 1, 4, 4), dtype=torch.float)
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2), return_indices=True)
# 注意这里是保存了最大值所在的索引
img_pool, indices = maxpool_layer(img_tensor)
# unpooling
img_reconstruct = torch.randn_like(img_pool, dtype=torch.float)
maxunpool_layer = nn.MaxUnpool2d((2, 2), stride=(2, 2))
img_unpool = maxunpool_layer(img_reconstruct, indices)
print("raw_img:\n{}\nimg_pool:\n{}".format(img_tensor, img_pool))
print("img_reconstruct:\n{}\nimg_unpool:\n{}".format(img_reconstruct, img_unpool))
输出如下:
# pooling
img_tensor = torch.randint(high=5, size=(1, 1, 4, 4), dtype=torch.float)
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2), return_indices=True)
img_pool, indices = maxpool_layer(img_tensor)
# unpooling
img_reconstruct = torch.randn_like(img_pool, dtype=torch.float)
maxunpool_layer = nn.MaxUnpool2d((2, 2), stride=(2, 2))
img_unpool = maxunpool_layer(img_reconstruct, indices)
print("raw_img:\n{}\nimg_pool:\n{}".format(img_tensor, img_pool))
print("img_reconstruct:\n{}\nimg_unpool:\n{}".format(img_reconstruct, img_unpool))
线性层
线性层又称为全连接层,其每个神经元与上一个层所有神经元相连,实现对前一层的线性组合或线性变换。
代码如下:
inputs = torch.tensor([[1., 2, 3]])
linear_layer = nn.Linear(3, 4)
linear_layer.weight.data = torch.tensor([[1., 1., 1.],
[2., 2., 2.],
[3., 3., 3.],
[4., 4., 4.]])
linear_layer.bias.data.fill_(0.5)
output = linear_layer(inputs)
print(inputs, inputs.shape)
print(linear_layer.weight.data, linear_layer.weight.data.shape)
print(output, output.shape)
输出为:
tensor([[1., 2., 3.]]) torch.Size([1, 3])
tensor([[1., 1., 1.],
[2., 2., 2.],
[3., 3., 3.],
[4., 4., 4.]]) torch.Size([4, 3])
tensor([[ 6.5000, 12.5000, 18.5000, 24.5000]], grad_fn=<AddmmBackward>) torch.Size([1, 4])
激活函数层
假设第一个隐藏层为: H 1 = X × W 1 H_{1}=X \times W_{1} H1=X×W1,第二个隐藏层为: H 2 = H 1 × W 2 H_{2}=H_{1} \times W_{2} H2=H1×W2,输出层为:
Output = H 2 ∗ W 3 = H 1 ∗ W 2 ∗ W 3 = X ∗ ( W 1 ∗ W 2 ∗ W 3 ) = X ∗ W \begin{aligned} \text { Output } &=\boldsymbol{H}_{\mathbf{2}} * \boldsymbol{W}_{\mathbf{3}} \\ &=\boldsymbol{H}_{1} * \boldsymbol{W}_{\mathbf{2}} * \boldsymbol{W}_{\mathbf{3}} \\ &=\boldsymbol{X} *\left(\boldsymbol{W}_{1} * \boldsymbol{W}_{\mathbf{2}} * \boldsymbol{W}_{3}\right) \\ &=\boldsymbol{X} * \boldsymbol{W} \end{aligned} Output =H2∗W3=H1∗W2∗W3=X∗(W1∗W2∗W3)=X∗W
如果没有非线性变换,由于矩阵乘法的结合性,多个线性层的组合等价于一个线性层。
激活函数对特征进行非线性变换,赋予了多层神经网络具有深度的意义。下面介绍一些激活函数层。
nn.Sigmoid
- 计算公式: y = 1 1 + e − x y=\frac{1}{1+e^{-x}} y=1+e−x1
- 梯度公式: y ′ = y ∗ ( 1 − y ) y^{\prime}=y *(1-y) y′=y∗(1−y)
- 特性:
- 输出值在(0,1),符合概率
- 导数范围是 [0, 0.25],容易导致梯度消失
- 输出为非 0 均值,破坏数据分布

nn.tanh
- 计算公式: y = sin x cos x = e x − e − x e − + e − x = 2 1 + e − 2 x + 1 y=\frac{\sin x}{\cos x}=\frac{e{x}-e{-x}}{e{-}+e{-x}}=\frac{2}{1+e^{-2 x}}+1 y=cosxsinx=e−+e−xex−e−x=1+e−2x2+1
- 梯度公式: y ′ = 1 − y 2 y{\prime}=1-y{2} y′=1−y2
- 特性:
- 输出值在(-1, 1),数据符合 0 均值
- 导数范围是 (0,1),容易导致梯度消失

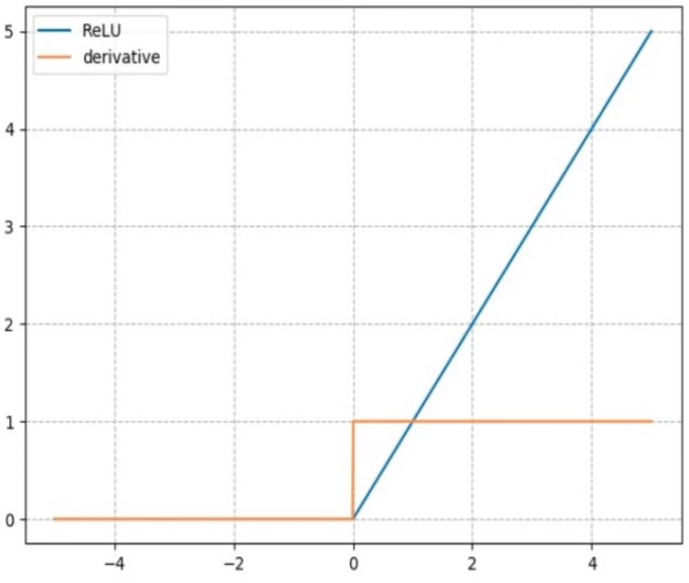
nn.ReLU(修正线性单元)
- 计算公式: y = m a x ( 0 , x ) y=max(0, x) y=max(0,x)
- 梯度公式: y ′ = { 1 , x > 0 undefined, x = 0 0 , x < 0 y^{\prime}=\left\{\begin{array}{ll} 1, & x>0 \\ \text { undefined, } & x=0 \\ 0, & x<0 \end{array}\right. y′=⎩ ⎨ ⎧1, undefined, 0,x>0x=0x<0
- 特性:
- 输出值均为正数,负半轴的导数为 0,容易导致死神经元
- 导数是 1,缓解梯度消失,但容易引发梯度爆炸
针对 RuLU 会导致死神经元的缺点,出现了下面 3 种改进的激活函数。
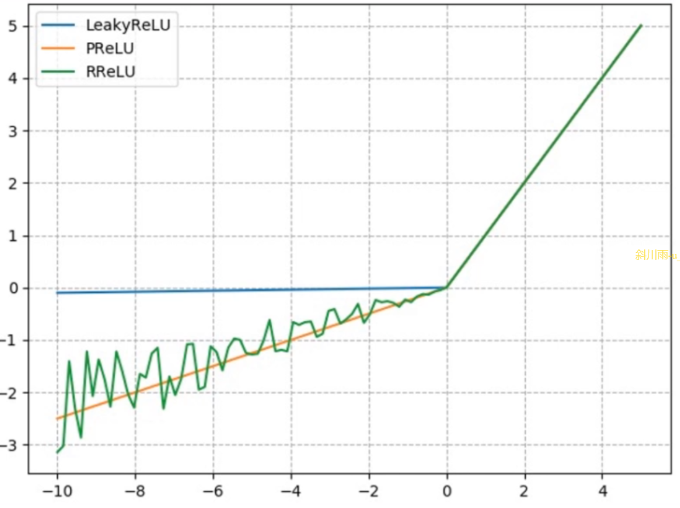
nn.LeakyReLU
- 有一个参数
negative_slope:设置负半轴斜率
nn.PReLU
- 有一个参数
init:设置初始斜率,这个斜率是可学习的
nn.RReLU
R 是 random 的意思,负半轴每次斜率都是随机取 [lower, upper] 之间的一个数
- lower:均匀分布下限
- upper:均匀分布上限