第3章简单的优化模型

关键词：简单优化微分法建模思想

本章与第4章连续两章都是优化、规划的问题，可以看成一类问题——内容上也是由简单到复杂。在第3章中，主要是几个简单的优化模型，可以归结到函数极值问题来求解，直接用微分法。虽然模型、数学计算难不倒，但是还是那句——建模，求解之后结果分析、结果解释的思想，是我们要学习和引入脑中的。

3.1 存储模型
允许缺货两种讨论，中间推出一个最小费用的结果——经济订货批量公式。对存储量函数作图，观察规律，对结果解释。

3.2 生猪出售时机
关键点在于敏感性分析和强健性分析——这对于优化模型是否实用、有效是很重要的。

3.3 森林救火
亮点是对火势蔓延程度的形式作出的数条假设，以及假设对应的实际解释。只要合理、自圆其说，就是一个好的对实际问题的简化算法。

3.4 最优价格
主要是引出边际收入、编辑支出，以及经济学一条著名定律——最大利润在边际收入等于编辑支持时达到。

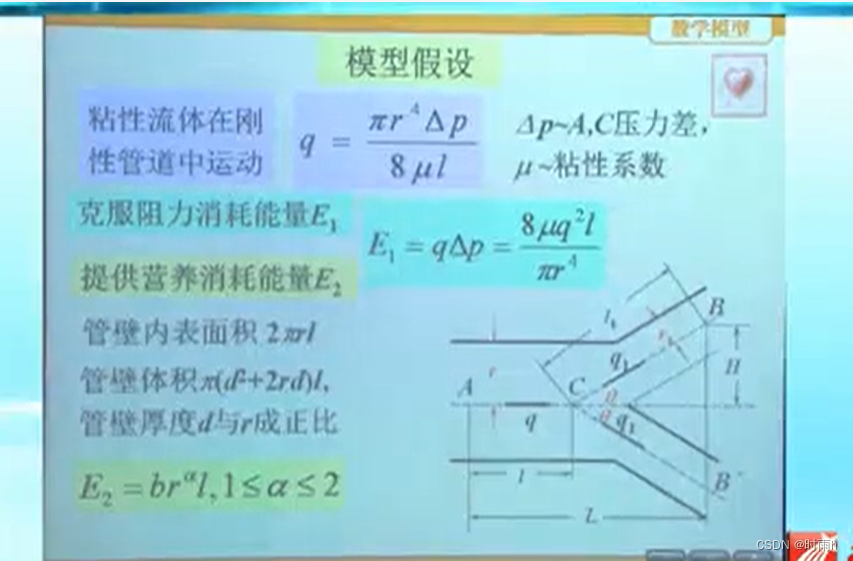
3.5 血管分支
是很有趣的一节，用数学模型研究生理问题，我们还是只关注建模、数学的层面，而对于血管系统几何形状等生理学知识不讨论过多，用合理有力的假设代之。

3.6 消费者的选择
一个消费者买两种产品时，钱应该如何分配。分配比例使他得到最大的满意度的最优比例乘务消费者均衡，而建立消费者均衡模型的关键在于确定效用函数。

3.7 冰山运输
也是很有趣的问题，考虑各种因素，基于一些假设，这节研究怎样运输冰山使费用最小。其中用实际数据建立了经验公式，二是假设冰山为球形，简化了融化规律等的计算。
在这里插入图片描述

在这里插入图片描述

允许缺货的情况

在这里插入图片描述

血管模型

在这里插入图片描述

第4章数学规划模型

关键词：数学规划方法 lingo/lindo软件结果深入分析变量个数

约束条件、可行域、目标函数，构成了常说的“数学规划”模型。本章揭示了数学规划的本质，和它与传统优化数学问题的区别：常理优化模型属于函数极值问题的范畴，但实际中更多的是决策变量数、约束个数较大，且最优解往往在边界上取得的问题，因此不能用传统的“微分法”求解——因此要引入“数学规划”方法。

这一章内容不少，但都是一类问题，主要点有几个：

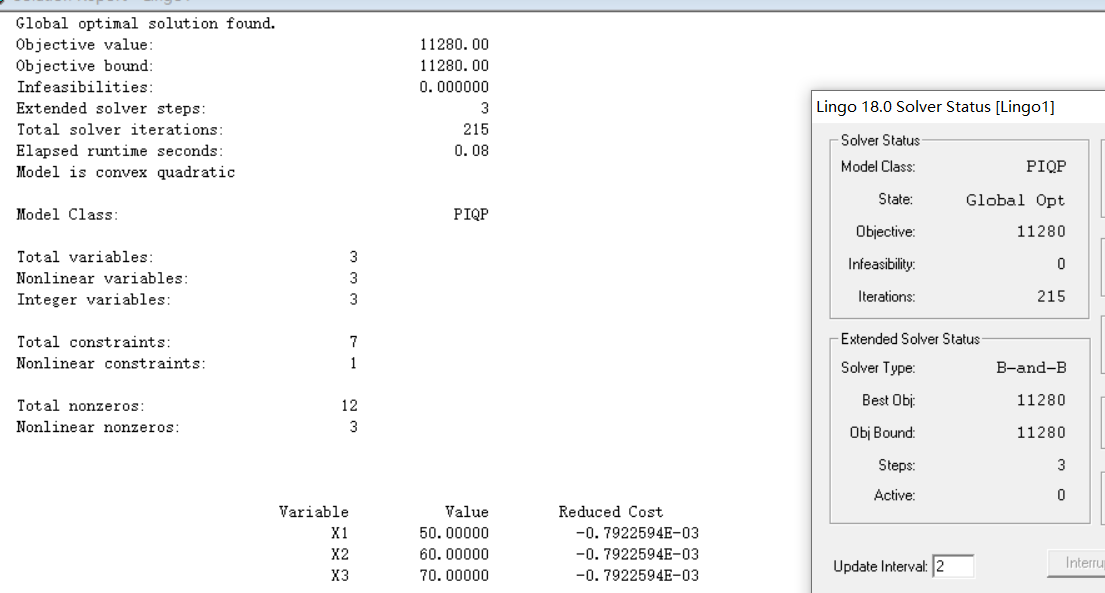
lingo、lindo求解的使用——运行结果中还有一些平时未留意的信息，可以作为结果分析来用，前两节叙述较多；
一些细节之处：把一句话用数学公式表达，它往往作为约束条件，如p102的式（19）；
多目标规划的处理，p109的“选课策略”——基本思想是通过加权组合形成一个新的目标，从而化为单目标规划；
同前面章节一样地，对一个问题解出结果后，问题虽然解决了，但分析并没有结束——我们要学习这种further discussion的精神，发现这个结果“恰与…相同…”之类的，不妨多问自己一句：“这是偶然的吗？”然后继续分析，得出一般的结论，这样往往能看到更多的风景，得出的结论更有含金量/启发性，而不是仅仅是解决了该个问题而已。如p109选课策略。
减少变量个数，简化模型、式子（简化起见，同时lingo对变量个数有限制），p115销售的例子。
求最优解时，为了减少搜索范围，加快速度，可以先去一个特殊情况求出一个可行解，然后让最优解至少优于它。

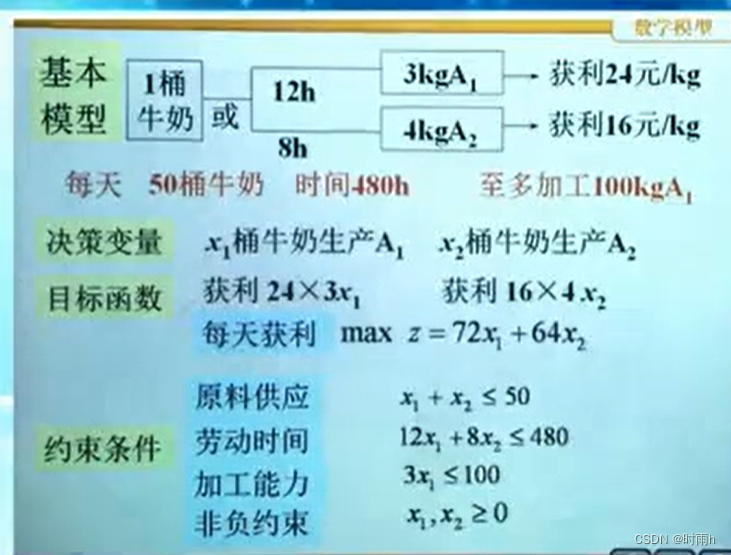
奶制品的生产销售

在这里插入图片描述
奶制品的生产销售是一个复杂的过程，需要考虑多个因素来进行数学建模。以下是一些可能的建模要素：

生产成本：包括原料成本、劳动力成本、设备成本等。这些成本可以用数学公式表示，并考虑到不同产品的成本差异。
生产容量：根据工厂的产能限制，确定每种奶制品的最大生产量。这可以通过制约条件来表示，例如生产时间、设备能力等。
供应链管理：考虑供应商和配送渠道，建立供应链网络模型来确定最佳的原料采购和产品分销策略。
需求预测：通过历史数据或市场调研，预测不同奶制品的需求量。这可以使用时间序列分析、回归模型等方法进行建模。
库存管理：根据需求预测和生产计划，确定合理的库存水平和补充策略，以避免库存过剩或缺货的情况。
客户满意度：考虑客户对不同产品的偏好和满意度，建立数学模型来优化产品组合和定价策略，以最大化客户满意度和市场份额。
销售预测：基于市场营销活动、竞争情况等因素，预测不同奶制品的销售量，并制定相应的销售策略。

综上所述，奶制品的生产销售数学建模涉及到成本、产能、供应链、需求预测、库存管理、客户满意度和销售预测等多个方面。通过合理的建模和优化方法，可以提高生产效率、降低成本，实现可持续发展和市场竞争优势。

在这里插入图片描述

当涉及奶制品的生产销售数学建模时，还可以考虑以下因素：

品质控制：建立质量控制模型来监测和控制奶制品的生产过程中的质量问题，以确保产品符合标准和客户要求。
季节性因素：考虑不同季节对奶制品需求的影响，以及季节性波动对生产计划和库存管理的影响。例如，夏季对冰淇淋的需求可能更高。
资源优化：考虑资源利用效率，如能源、水资源等。可以建立数学模型来优化资源的使用，以降低生产成本和环境影响。
产品组合优化：考虑不同奶制品之间的互补性和替代性，通过建立数学模型来确定最佳产品组合，以实现销售收入最大化。
价格策略：通过建立定价模型，考虑市场需求、成本和竞争情况，确定最佳的产品定价策略，以实现利润最大化或市场份额最大化。
营销策略：将市场推广、促销活动和广告投放纳入数学建模，以优化市场营销策略，增加产品曝光度和销售量。
风险管理：考虑生产过程中的不确定性因素，如原材料价格波动、需求波动、供应链中断等，建立风险管理模型，以最小化风险和损失。

通过对上述因素的数学建模和优化，可以帮助奶制品生产销售企业做出更科学和有效的决策，提高生产效率、降低成本、增加利润，并满足客户需求。
在这里插入图片描述
无约束优化是指在没有任何约束条件下，寻找函数的最大值或最小值的问题。在奶制品生产销售中，无约束优化可以应用于以下方面：

生产成本最小化：通过优化生产过程中的各项成本，包括原材料成本、劳动力成本和设备成本等，以达到生产成本的最小化。
销售利润最大化：通过优化定价策略、产品组合和市场营销策略等因素，以实现销售利润的最大化。
生产效率最大化：优化生产资源的分配和利用，以提高生产效率，最大限度地利用可用资源。
产品质量优化：通过优化生产过程中的参数和控制变量，以实现产品质量的最佳化。
生产能力最大化：通过优化工厂的产能规划和生产调度，以最大化生产能力，并满足市场需求。

在进行无约束优化时，可以使用各种数学方法和优化算法，如梯度下降法、牛顿法、遗传算法等。这些方法可以帮助找到函数的最大值或最小值，并提供更优的生产销售决策。
在这里插入图片描述

在这里插入图片描述

约束优化的简单分类

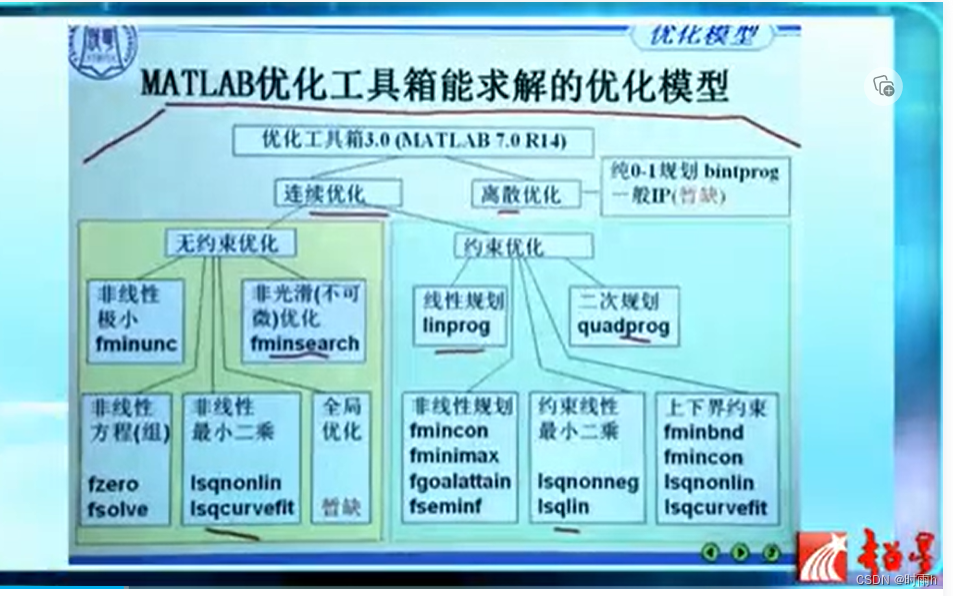
在这里插入图片描述

MATLAB提供了一个强大的优化工具箱，用于解决各种无约束和有约束的优化问题。该工具箱包含了多种优化算法和函数，可以帮助用户寻找函数的最大值或最小值。

以下是MATLAB优化工具箱中常用的函数和算法：

fminunc：用于无约束优化问题的函数。它使用基于梯度的方法（如拟牛顿法、共轭梯度法）在局部最小值处寻找函数的最小值。
fminsearch：也是用于无约束优化的函数，但它不要求提供梯度信息。它使用模拟退火等全局搜索算法来寻找函数的最小值。
fmincon：用于有约束优化问题的函数。它可以处理等式约束、不等式约束和边界约束，并使用内点法等算法来求解最小化问题。
lsqnonlin：用于非线性最小二乘问题的函数。它通过最小化残差向量来寻找最优解，可以处理等式约束和不等式约束。

除了上述函数之外，MATLAB优化工具箱还提供了许多其他函数和工具，如fminimax用于极小极大问题、patternsearch用于模式搜索、ga用于遗传算法等。

使用MATLAB优化工具箱，您可以通过编写适当的目标函数和约束条件，并选择合适的优化算法，来解决奶制品生产销售中的各种优化问题，从而提高效率、降低成本或最大化利润。
以下是使用MATLAB优化工具箱解决一个无约束优化问题的简单示例：

假设有一个目标函数 f(x) = x^2 + 3x + 2，我们的目标是找到使得该函数取得最小值的 x 值。

% 定义目标函数
f = @(x) x^2 + 3*x + 2;

% 调用优化函数 fminunc
x0 = 0;  % 初始猜测值
x_opt = fminunc(f, x0);

% 输出最优解和最优值
fprintf('最优解 x = %f\n', x_opt);
fprintf('最优值 f(x) = %f\n', f(x_opt));