1、多元线性回归模型：定义：具有多个特征的线性回归模型

• 多元线性回归模型，见下图：
  
• 多元线性回归总结（参数、模型、损失函数、梯度下降算法）见下图：【注意：梯度下降算法每次都是同时更新w_j和b】
  

2、多维特征：

• 多维特征：{x₁、x₂、…、x_n}，其中x_j表示第j个特征
  • n表示特征的数量
  • 具体解释如下图：
    

---

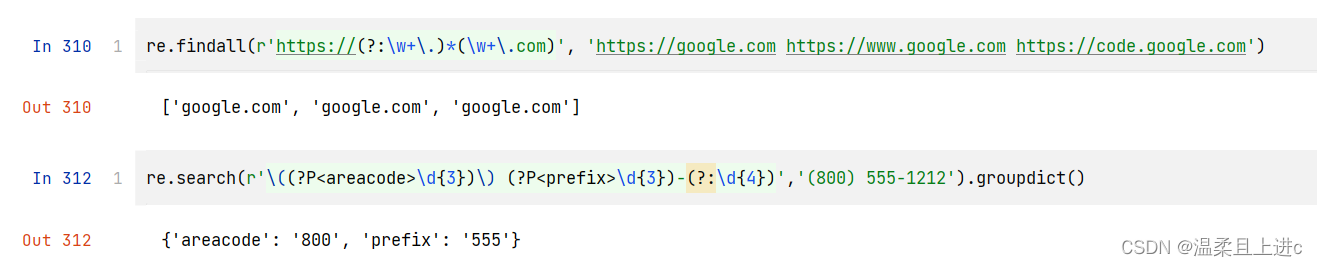
3、矢量化（vectorization）

• 工具：使用Numpy库，Numpy库是python中，机器学习使用最广泛的数值线性库
• 优点：
  • 1、简化代码
  • 2、提升运算速度，具体解释见下面两幅图
  • 3、提升代码可阅读性
    
    

4、多元线性回归的梯度下降算法：用矢量化（python当中的Numpy库）实现，可以通过硬件并行计算提升运行速度

5、正规方程（Normal equation）：仅适用于线性回归求解w和b，不能推广到其他算法，线性数量过大时，该方法速度会变慢，相比之下，在回归算法以及其他算法中，梯度下降是寻找w和b的推荐算法。

6、缩放不同特征：【特征就是模型的输入x_j】

• 原因：特征范围跨度会影响梯度下降算法的速度，见下图（以房价预测为例）：
  
• 可以用来缩放特征的方法，见下图：
  • 方法一：
    
  • 方法二：
    
  • 方法三：
    
• 特征缩放的技巧：
  
• 如何检查损失函数有没有收敛【通过J-iteration图，其中J为损失函数，iteration为w和b的迭代次数】
  

7、特征工程：找到适合作为特征的输入x_j

8、多项式回归：可以获得更好的曲线模型【选择合适的多项式函数来拟合训练样本】

9、scikit-learn：一个非常广泛使用的python开源机器学习库【注意：了解回归原理非常重要，单纯调用scikit-learn当中的函数，就像使用一个黑盒。】

总结：

• 线性回归中的单变量线性回归是理解线性回归的基础，多项式回归是更为复杂的一种回归模型
• 回归的过程就是通过寻找合适的参数w和b使得损失函数最小
• 梯度下降过程的速度受到特征范围的影响