文章目录
- 1. 命题与联结词
- 1.1 命题
- 1.2 常用联结词
- 1.3 命题公式
- 1.4 命题的等值演算与推理
- 等价关系式
- 基本等价式
1. 命题与联结词
1.1 命题
命题:我们对确定对象做出的陈述句称为命题(propositions and statements 命题或陈述)。当判断为真时,该命题为真,否则为假。
今天下雨 是命题 √
你在干什么啊 非陈述句 X
我只给所有不给自己理发的人理发 悖论 X
原子命题:通常把不含有逻辑联结词的命题称为原子命题或原子(atoms)
复合命题:把由原子命题和逻辑联结词共同组成的命题称为复合命题(compositive propositions or compound statements 综合命题或复合命题)。
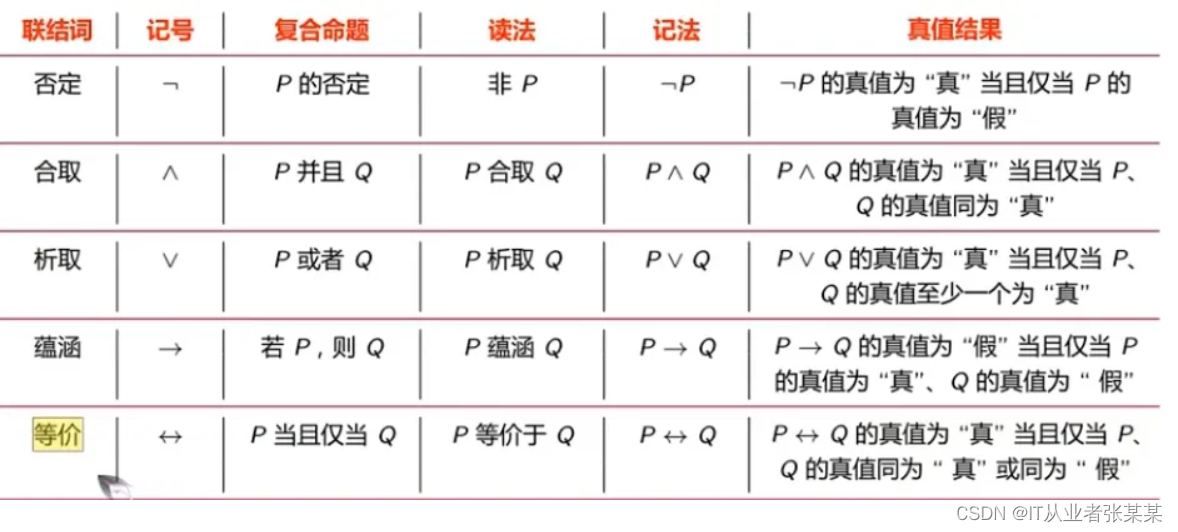
1.2 常用联结词
否定:符号
¬
\neg
¬ 称作否定联结词
合取: 符号
∧
\wedge
∧称作合取联结词
析取: 符号
∨
\vee
∨称作析取联结词 .
蕴含或条件: 符号
→
\to
→称作蕴含或条件联结词 .
双向蕴含或等价: 符号
↔
\leftrightarrow
↔称作双向蕴含或等价联结词 .
联结词优先级
(
)
()
() >
¬
\neg
¬ >
∧
\wedge
∧ >
∨
\vee
∨ >
→
\to
→ >
↔
\leftrightarrow
↔
1.3 命题公式
命题常元:代表特定的简单命题
命题变元:代表任意命题,取值为真或假的变量
命题公式:含有命题变元的表达式。即
P
∨
Q
P \vee Q
P∨Q便是一个命题公式
公式的赋值
定义:若命题公式
A
A
A含有的全部命题变元为
p
1
,
p
2
,
p
3
,
p
4
…
p
n
p_1,p_2,p_3,p_4…p_n
p1,p2,p3,p4…pn,给
p
1
,
p
2
,
p
3
,
p
4
…
p
n
p_1,p_2,p_3,p_4…p_n
p1,p2,p3,p4…pn指定一组真值,称为
A
A
A的一个解释或赋值。使
A
A
A的真值为真的赋值称为成真赋值,使A的真值为假的赋值为成假赋值。
指派或赋值:用
α
,
β
\alpha,\beta
α,β等表示当
A
A
A对取值状况
α
\alpha
α为真时,称指派
α
\alpha
α成真
A
A
A,或是
α
\alpha
α是
A
A
A的成真赋值。记为
α
(
A
)
=
1
\alpha\left(A\right)=1
α(A)=1
对一切可能的指派,公式
A
A
A的取值可用下表描述,真值表
真值表:命题公式在所有可能的赋值下的取值的列表含n个变形的公式有2的n次方个赋值。
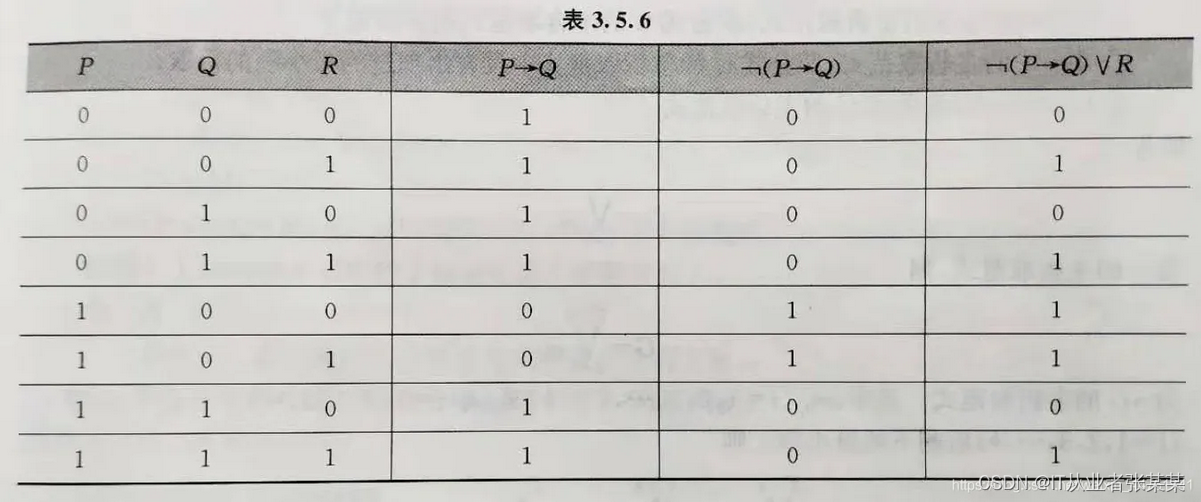
命题公式的分类
若A在它的各种情况下赋值的取值均为真,则称A为重言式或永真式
若A在它的各种情况下赋值的取值均为假,则称A为矛盾式或永假式
若至少存在一种赋值能使A的真值为真,则称A为可满足式
1.4 命题的等值演算与推理
等价关系式
逻辑等价:当命题公式
A
↔
B
A \leftrightarrow B
A↔B为重言式时,称
A
A
A逻辑等价于
B
B
B,记为
A
⇔
B
A \Leftrightarrow B
A⇔B
基本等价式
(1)双重否定律
¬
¬
⇔
A
\neg \neg \Leftrightarrow A
¬¬⇔A
(2)幂等律
A
∧
A
⇔
A
,
A
∨
A
⇔
A
A \wedge A \Leftrightarrow A,A \vee A \Leftrightarrow A
A∧A⇔A,A∨A⇔A
(3)交换律
A
∧
B
⇔
B
∧
A
,
A
∨
B
⇔
B
∨
A
A \wedge B \Leftrightarrow B \wedge A, A \vee B \Leftrightarrow B \vee A
A∧B⇔B∧A,A∨B⇔B∨A
(4)结合律
A
∧
(
B
∧
C
)
⇔
(
A
∧
B
)
∧
C
,
A
∨
(
B
∨
C
)
⇔
(
A
∨
B
)
∨
C
A \wedge (B \wedge C )\Leftrightarrow (A \wedge B) \wedge C , A \vee (B \vee C )\Leftrightarrow (A \vee B) \vee C
A∧(B∧C)⇔(A∧B)∧C,A∨(B∨C)⇔(A∨B)∨C
(5)分配律
A
∧
(
B
∨
C
)
⇔
(
A
∧
B
)
∨
(
A
∧
C
)
,
A
∨
(
B
∧
C
)
⇔
(
A
∨
B
)
∧
(
A
∨
C
)
A \wedge (B \vee C )\Leftrightarrow (A \wedge B) \vee (A \wedge C) , A \vee (B \wedge C )\Leftrightarrow (A \vee B) \wedge (A \vee C)
A∧(B∨C)⇔(A∧B)∨(A∧C),A∨(B∧C)⇔(A∨B)∧(A∨C)
(6)德摩根律
¬
(
A
∧
B
)
⇔
¬
A
∨
¬
B
,
¬
(
A
∨
B
)
⇔
¬
A
∧
¬
B
\neg (A \wedge B) \Leftrightarrow \neg A \vee \neg B , \neg (A \vee B) \Leftrightarrow \neg A \wedge \neg B
¬(A∧B)⇔¬A∨¬B,¬(A∨B)⇔¬A∧¬B
(7)吸收律
A
∧
(
A
∨
B
)
⇔
A
,
A
∨
(
A
∧
B
)
⇔
A
A \wedge (A \vee B )\Leftrightarrow A , A \vee (A \wedge B ) \Leftrightarrow A
A∧(A∨B)⇔A,A∨(A∧B)⇔A
(8)零律
A
∨
1
⇔
1
,
A
∧
0
⇔
0
A \vee 1 \Leftrightarrow 1 , A \wedge 0 \Leftrightarrow 0
A∨1⇔1,A∧0⇔0
(9)同一律
A
∧
1
⇔
A
,
A
∨
0
⇔
A
A \wedge 1 \Leftrightarrow A , A \vee 0 \Leftrightarrow A
A∧1⇔A,A∨0⇔A
(10)排中律
A
∨
¬
A
⇔
1
A \vee \neg A \Leftrightarrow 1
A∨¬A⇔1
(11)矛盾律
A
∧
¬
A
⇔
0
A \wedge \neg A \Leftrightarrow 0
A∧¬A⇔0
(12)蕴涵等值式
A
→
B
⇔
¬
A
∨
B
A \to B \Leftrightarrow \neg A \vee B
A→B⇔¬A∨B
(13)等价等值式
A
↔
B
⇔
(
A
→
B
)
∧
(
B
→
A
)
A \leftrightarrow B \Leftrightarrow (A \to B) \wedge (B \to A)
A↔B⇔(A→B)∧(B→A)
A
↔
B
⇔
(
¬
A
∨
B
)
∧
(
¬
B
∨
A
)
A \leftrightarrow B \Leftrightarrow (\neg A \vee B) \wedge (\neg B \vee A)
A↔B⇔(¬A∨B)∧(¬B∨A)
A
↔
B
⇔
(
A
∧
B
)
∨
(
¬
A
∧
¬
B
)
A \leftrightarrow B \Leftrightarrow (A \wedge B) \vee (\neg A \wedge \neg B)
A↔B⇔(A∧B)∨(¬A∧¬B)
(14)假言易位
A
→
B
⇔
¬
B
→
¬
A
A \to B \Leftrightarrow \neg B \to \neg A
A→B⇔¬B→¬A
(15)等价否定等值式
A
↔
B
⇔
¬
A
↔
¬
B
A \leftrightarrow B \Leftrightarrow \neg A \leftrightarrow \neg B
A↔B⇔¬A↔¬B
(16)归谬论
(
A
→
B
)
∧
(
A
→
¬
B
)
⇔
¬
A
(A \to B)\wedge (A \to \neg B) \Leftrightarrow \neg A
(A→B)∧(A→¬B)⇔¬A

逻辑蕴涵:当命题公式
A
→
B
A \rightarrow B
A→B为重言式时,称
A
A
A逻辑蕴涵
B
B
B,记为
A
⇒
B
A \Rightarrow B
A⇒B