文章目录
- SkipList
- 理解跳表从单链表说起
- 查找的时间复杂度
- 空间复杂度
- 插入数据
- 更高效的方式维护索引
- 代码实现索引的抽取
- 概率算法
- 举例插入元素
- 删除数据
- 总结
- 为什么Redis选择使用跳表而不是红黑树来实现有序集合
SkipList
理解跳表从单链表说起
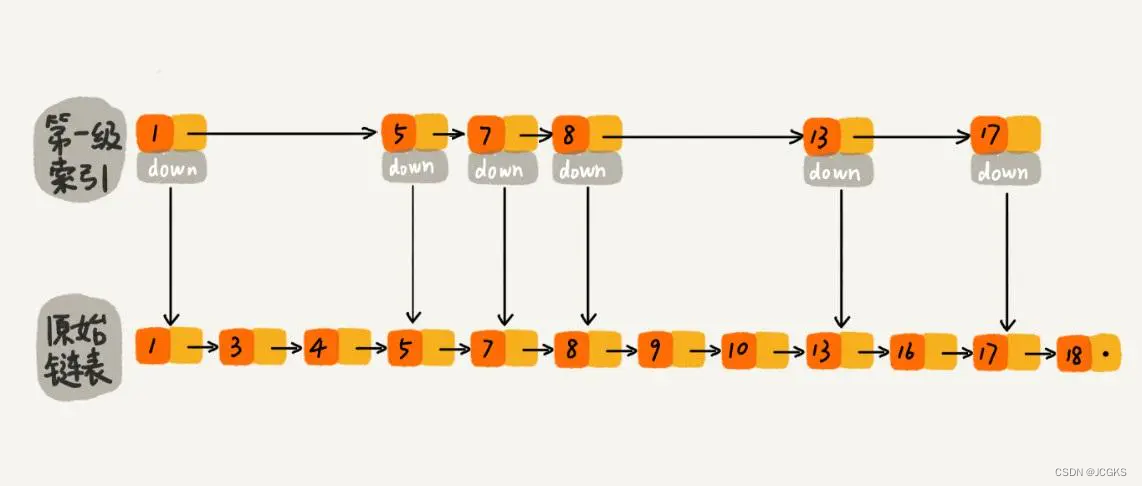
在原始单链表中查找元素,只能从头到尾一个一个的比较往后遍历,当数据量非常大的时候,时间复杂度会很高。于是考虑为单链表添加索引,在单链表的基础上添加一级索引,在一级索引的基础上添加二级索引…
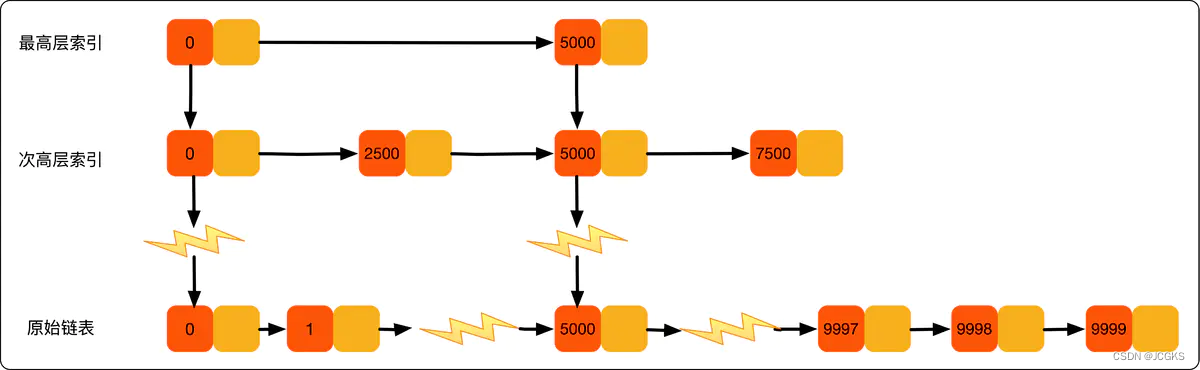
当数据量非常大的时候,优势就会很明显。
查找的时间复杂度
时间复杂度 = 索引的高度 * 每层索引遍历的元素的个数
原始链表有n个元素,一级索引有n/2个元素、二级索引有n/4个元素、k级索引有n/2^k
个元素。最高级索引一般有2个元素,2= n/(2^h) 即h = log2n-1;最高级索引h为索引层的高度加上原始数据一层,跳表的总高度为h = log2n。每一层最多遍历3个节点。所以查找的时间复杂度为O(3logn)省略常数即O(logn)
空间复杂度
假如原始链表包含n个元素,则一级索引元素个数为n/2、二级索引个数为n/4、三级索引元素个数为n/8以此类推,索引节点总和为n/2+n/4+n/8+…+8+4+2 = n-2空间复杂度为O(n)
如果每三个节点抽一个节点作为索引,索引总和数就是n/3+n/9+…+9+3 = n/2-1减少了一半。所以可以通过减少索引数减少空间复杂度,但是相应的肯定会造成查找效率有一定下降,可以根据我们的应用场景控制这个阈值
但是,索引节点往往只需要存储key和几个指针,并不需要存储完整的对象,所以当对象比较索引节点大很多时,索引占用的额外空间就可以忽略了。
插入数据
跳表的原始链表需要保持有序,所以会像查找元素一样,找到元素应该插入的位置,时间复杂度为O(logn)
如果一直往原始列表中添加数据,但是不更新索引,就可能出现索引节点之间数据非常多的情况,极端情况退化为单链表,从而使查找效率降低。
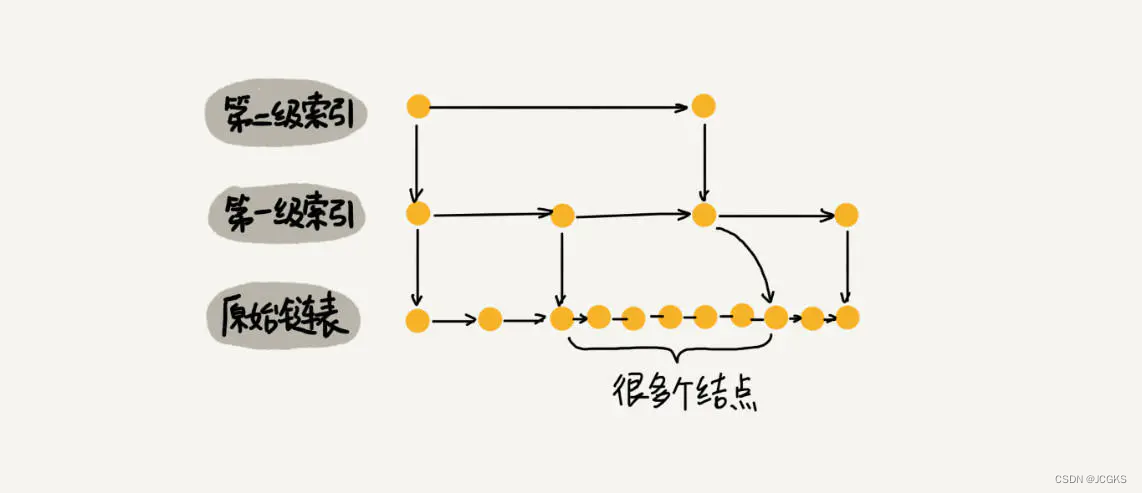 比较容易理解的做法就是完全重建索引,每次插入数据都把这个跳表的索引删除掉,然后重建。因为索引的空间复杂度是O(n),所以重建的时间复杂度是O(n),造成的后果是,为了维护索引导致每次插入数据的时间复杂度变成了O(n)
比较容易理解的做法就是完全重建索引,每次插入数据都把这个跳表的索引删除掉,然后重建。因为索引的空间复杂度是O(n),所以重建的时间复杂度是O(n),造成的后果是,为了维护索引导致每次插入数据的时间复杂度变成了O(n)
更高效的方式维护索引
在原始链表中随机选取n/2个元素作为一级索引是不是也能通过索引提高查找的效率?当然可以,因为一般随机选取的元素相对来说都比较均匀。如下图所示,随机选择n/2个元素作为一级索引,虽然不是每隔一个元素抽取一个,但是对于查找效率来讲,影响不大,比如想找元素16,仍然可以通过一级索引,使得遍历路径少了将近一半,如果抽取的一级元素恰好是前一半的元素1,3,4,5,7,8那么查找效率确实没有提升。但是这样的概率太小了。可以这样认为:当原始链表中元素数量足够大,且抽取足够随机,得到的索引是均匀的
代码实现索引的抽取
在每次插入新元素的时候,尽量让该元素有1/2的几率建立一级索引,1/4的几率建立二级索引,1/8的几率建立三级索引,以此类推,就能满足上面的条件。需要一个算法把控这个1/2、1/4…当每次有数据要插入时,先通过概率算法告诉我们这个元素要插入到几级索引中,然后开始维护索引并把数据插入到原始链表中。
概率算法
可以实现一个randomLevel()方法,该方法随即生成1~MAX_LEVEL之间的数(MAX_LEVEL表示索引的最高层数)该方法有1/2的概率返回1,1/4的概率返回2、1/8的概率返回3
- randomLevel()方法返回1表示当前插入的该元素不需要重建索引,只需要存储数据到原始链表中即可。
- randomLevel()方法返回2表示当前插入的该元素需要建立一级索引,(概率为1/4)
- randomLevel()方法返回3表示当前插入的该元素需要建立二级索引,(概率为1/8)
- randomLevel()方法返回4表示当前插入的该元素需要建立三级索引,(概率为1/16)
- …
当建立二级索引的时候,同时也会建立一级索引;当建立三级索引的时候,同时也会建立一二级索引。所以一级索引的个数等于 = 原始链表元素个数 * [randomLevel()>1的概率]
也就是n ** (1-1/2) = n/2;以此类推…
//该randomLevel()算法会随机生成一个1~maxlevel之间的数,且:
// 1/2的概率返回1
// 1/4的概率返回2
// 1/8的概率返回3
int randomLevel(){
int level = 1;
//当level < MAX_LEVEL,且随机数小于设定的晋升概率时,level+1
while(random()<SKIPLIST_P && level < MAX_LEVEL){
//random()产生0-1中间的随机数
level+=1;
}
return level;
}
这里的SKIPLIST_P为1/2;如果想节省空间利用率可以适当降低SKIPLIST_P的值从而减少索引个数REdis的zset中的SKIPLIST设定为0.25

元素插入到单链表的时间复杂度为O(1),索引的高度最多为logn当插入一个元素x时,最坏的情况就是元素x需要插入到每层索引中,最坏的时间复杂度为O(logn)
举例插入元素
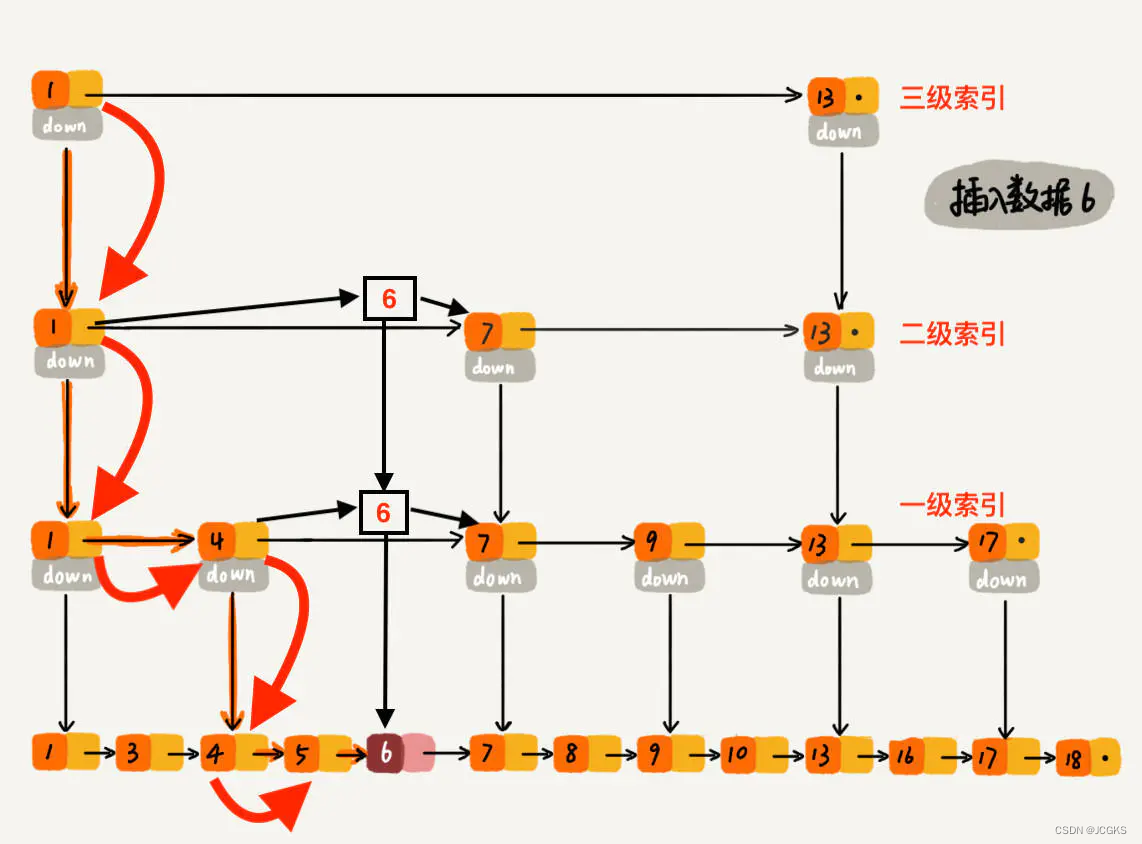
要插入数据 6 到跳表中,首先 randomLevel() 返回 3,表示需要建二级索引,即:一级索引和二级索引需要增加元素 6。该跳表目前最高三级索引,首先找到三级索引的 1,发现 6 比 1大比 13小,所以,从 1 下沉到二级索引。
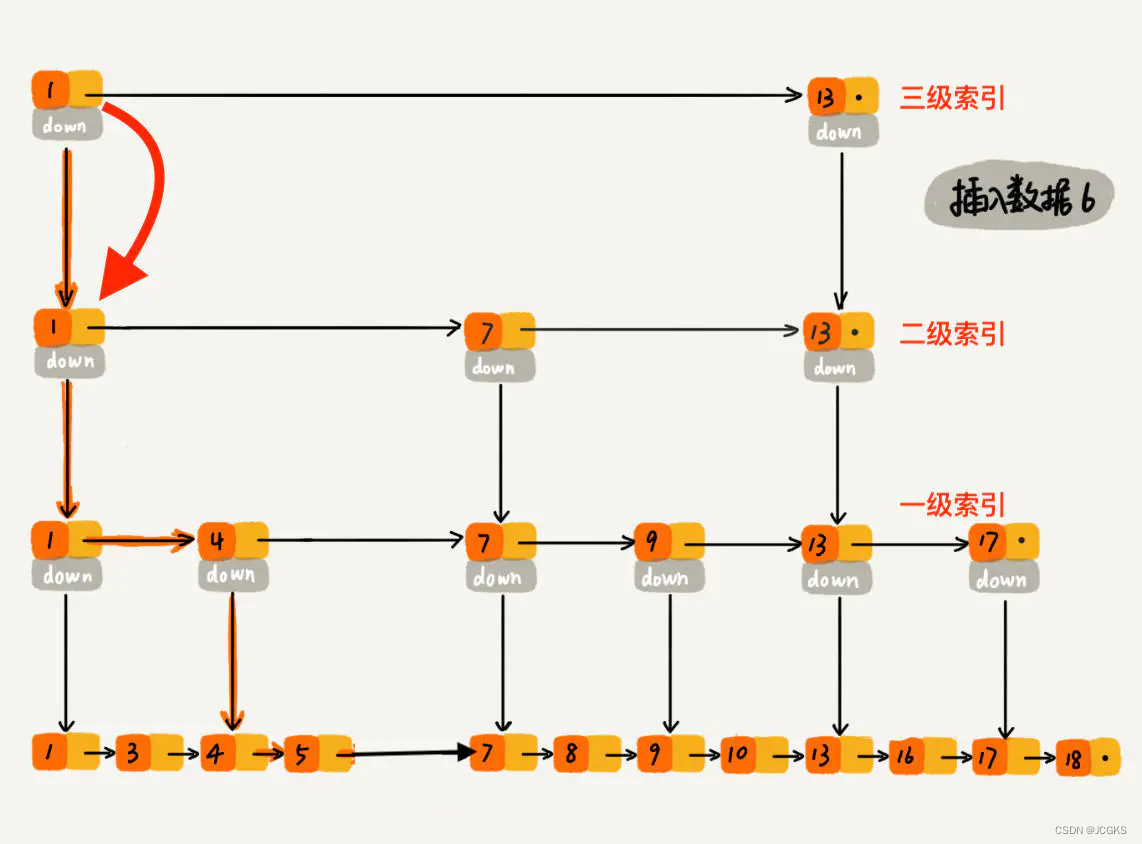
下沉到二级索引后,发现 6 比 1 大比 7 小,此时需要在二级索引中 1 和 7 之间加一个元素6 ,并从元素 1 继续下沉到一级索引
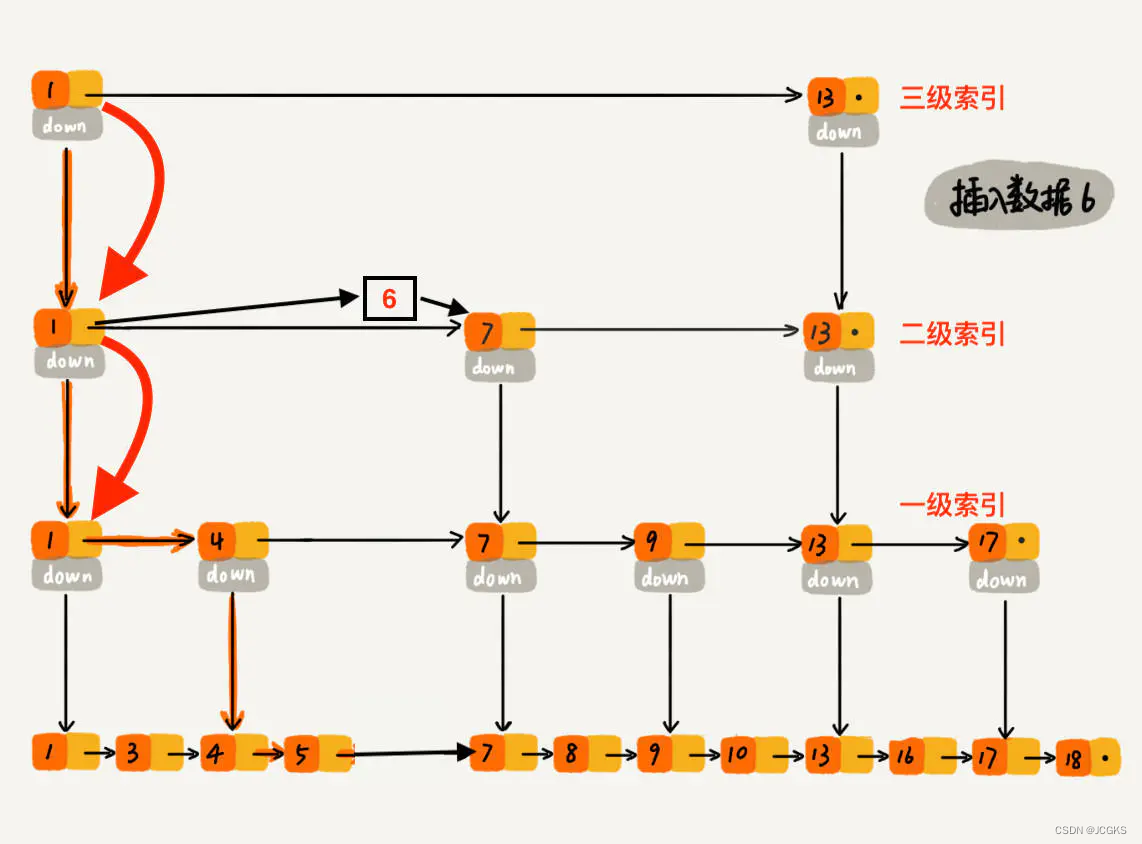
下沉到一级索引后,发现 6 比 1 大比 4 大,所以往后查找,发现 6 比 4 大比 7 小,此时需要在一级索引中 4 和 7 之间加一个元素 6 ,并把二级索引的 6 指向 一级索引的 6,最后,从元素 4 继续下沉到原始链表。
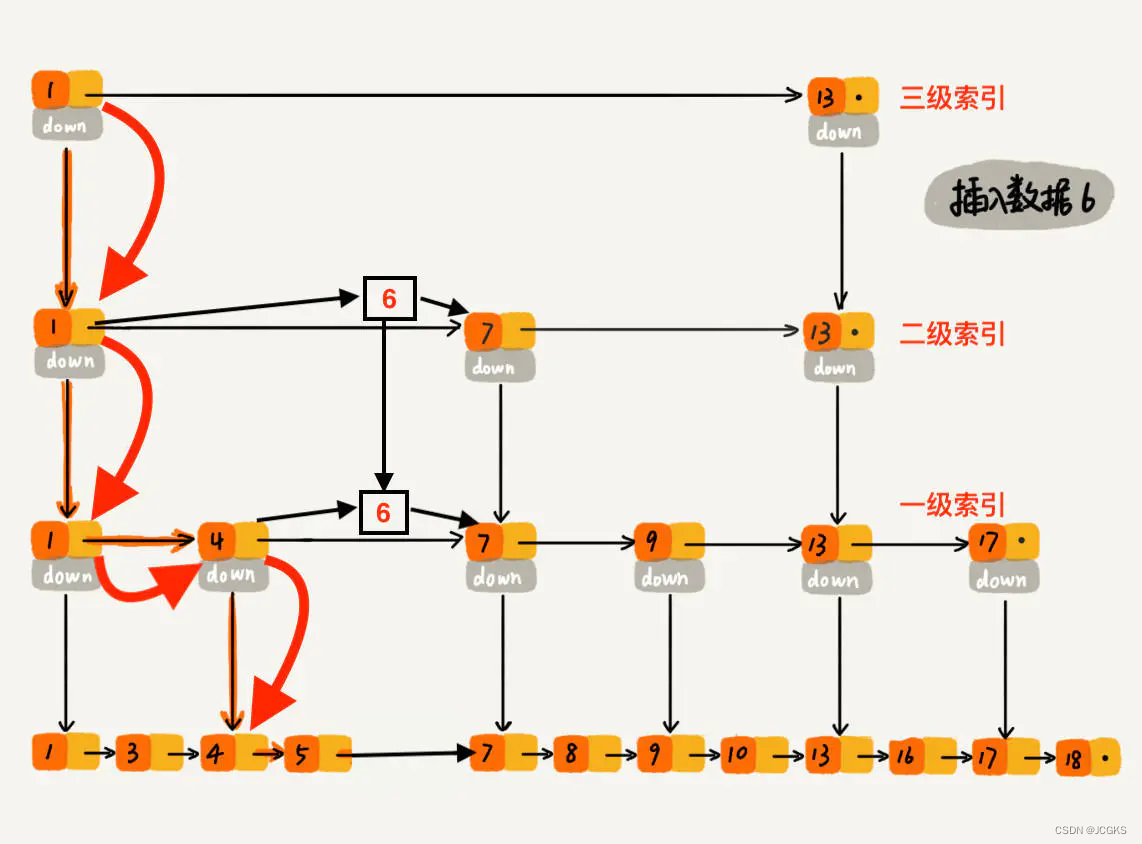
下沉到原始链表后,就比较简单了,发现 4、5 比 6小,7比6大,所以将6插入到 5 和 7 之间即可,整个插入过程结束。
删除数据
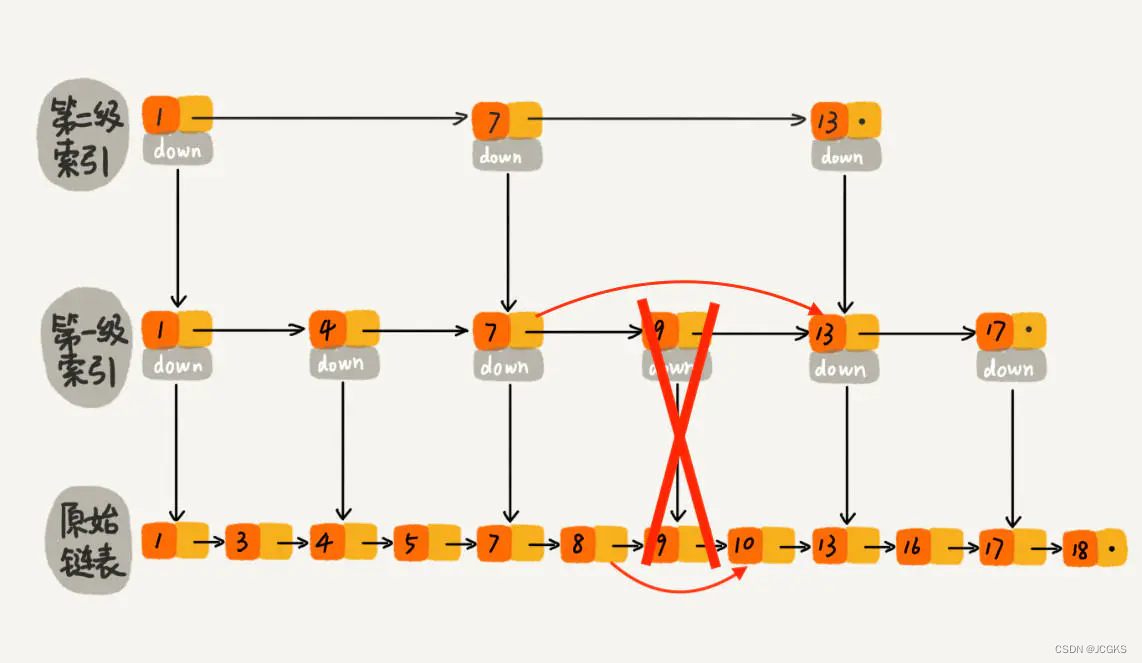
时间复杂度为O(logn)。删除节点其对应的索引也要删除
总结
- 跳表是实现二分查找的有序链表
- 每个元素插入时随机生成它的level
- 最低层包含所有元素
- 如果一个元素出现在level(x)那么它一定出现在x以下的level中
- 每个索引节点包含两个指针一个向下一个向右(但是各种跳表源码包括redis的zset都没有向下的指针)
- 跳表查询删除插入的时间复杂度都是O(logn)与平衡二叉树接近
为什么Redis选择使用跳表而不是红黑树来实现有序集合
插入一个元素
删除一个元素
查找一个元素
有序输出所有元素
按照范围区间查找元素(比如[100,356])
其中前四个操作红黑树也可以完成,且时间复杂度跟跳表是一样的但是,按照区间查找数据这个操作,红黑树的效率没有跳表高。