目录
- Explicit Representations in Computer Graphics(计算机图形学中的显式几何表示)
- Point Cloud(点云)
- Polygon Mesh(多边形网格)
- The Wavefront Object File(.obj) Format(OBJ格式文件)
- Curves(曲线)
- Bezier Curves(贝塞尔曲线)
- Defining Cubic Bezier Curve With Tangents(定义带切线的贝塞尔曲线)
- Bezier Curces - de Casteljau Algorithm(贝塞尔曲线的绘制算法)
- Evaluating Bezier Curves Algebraic Formula(贝塞尔曲线的代数表示)
- Properties of Bezier Curves(贝塞尔曲线的性质)
- Piecewise Bezier Curves(分段的贝塞尔曲线)
- Piecewise Bezier Curve - Continuity(分段贝塞尔曲线的连续性)
- Other types of splines(其它种类的样条)
- Surfaces(曲面)
- Bezier Surfaces(贝塞尔曲面)
- 参考
Explicit Representations in Computer Graphics(计算机图形学中的显式几何表示)
在图形学中有许多几何的显式的表示方式:
- Triangle meshes(三角网格)
- Bezier surfaces(贝塞尔曲面)
- Subdivision surfaces(细分曲面)
- NURBS(非均匀有理B样条)
- Point Clouds(点云)
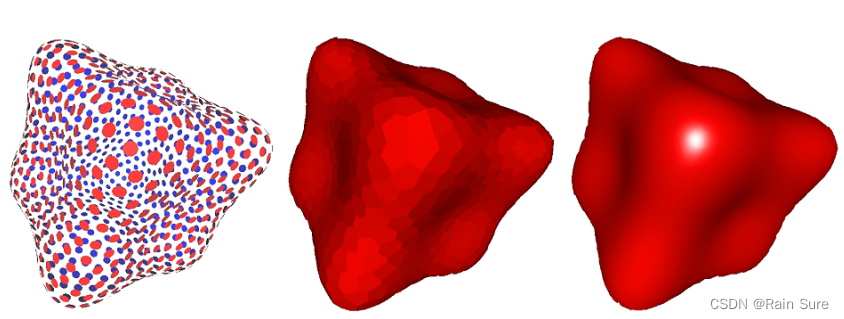
Point Cloud(点云)
最简单的表示方式:给定一些点的集合 ( x , y , z ) (x, y, z) (x,y,z)
可以很容易表示任何形状的几何。
对于大型数据集非常有效。
通常会被转换为多边形网格。
在采样不足的区域难以绘制。
Polygon Mesh(多边形网格)
该方法用的最多的方法,得到了最广泛的应用。
尤其是三角形和四边形。
更容易做处理、模拟、自适应采样等。
在三角形之间的连接关系等,需要更复杂的数据结构。

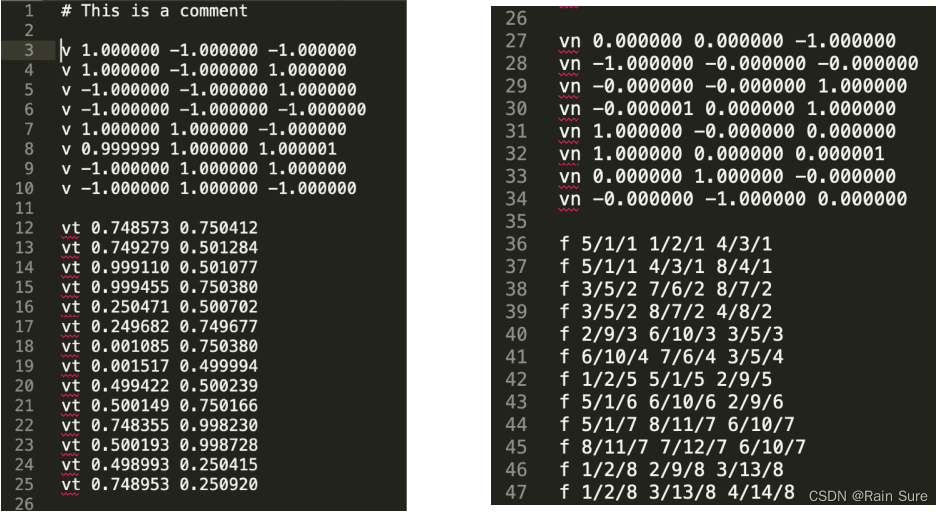
The Wavefront Object File(.obj) Format(OBJ格式文件)
这是一种文本文件,将顶点、法线、纹理坐标分别进行表示,并存储各个顶点和面的连接关系等。
通常用于图形学的研究。
Curves(曲线)
Bezier Curves(贝塞尔曲线)
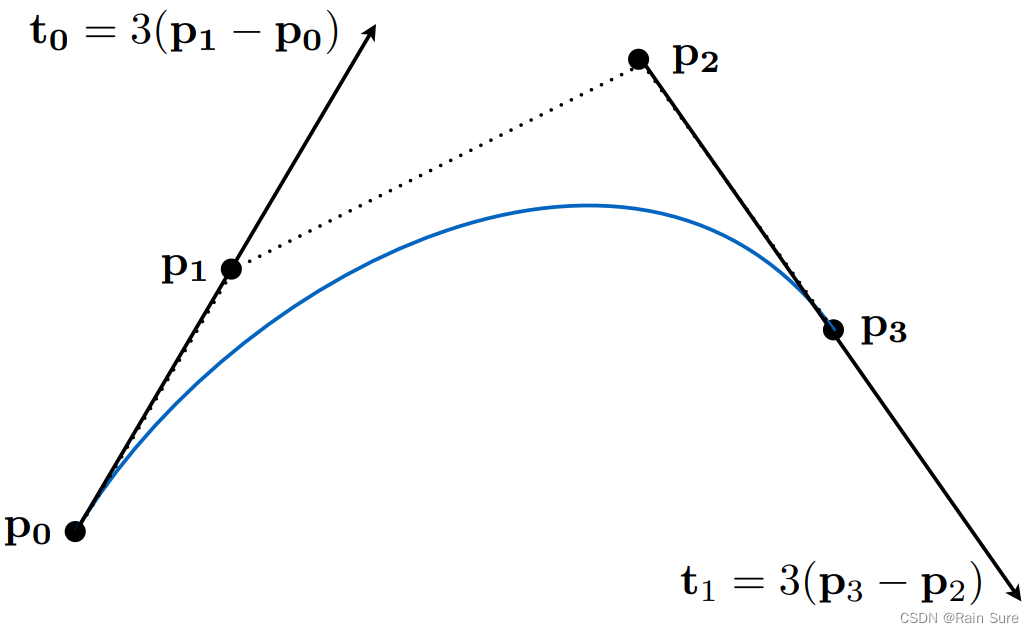
Defining Cubic Bezier Curve With Tangents(定义带切线的贝塞尔曲线)
给定一些控制点。
起始点和终止点一定需要在 p 0 p_0 p0和 p 3 p_3 p3上。
起始点的斜率必须要在 p 0 p 1 p_0p_1 p0p1方向,终止点的斜率必须要在 p 2 p 3 p_2p_3 p2p3方向。
并不要求曲线一定经过所有控制点。
Bezier Curces - de Casteljau Algorithm(贝塞尔曲线的绘制算法)
考虑给定三个控制点的贝塞尔曲线(二次贝塞尔曲线)。
假定 b 0 b_0 b0是在时间 t = 0 t = 0 t=0时的点, b 1 b_1 b1是在时间 t = 1 t = 1 t=1的点。
现在问题转换为,给定任意一个时间 t ∈ [ 0 , 1 ] t \in [0, 1] t∈[0,1],求出这个曲面上的点应该位于哪里?
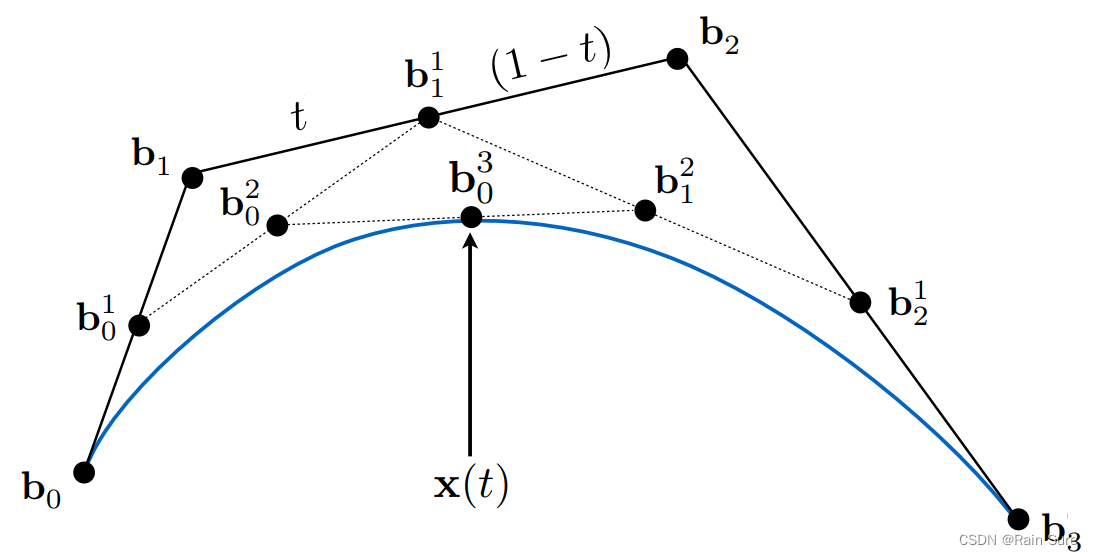
假设,现在我们需要找到 t = 1 3 t = \frac{1}{3} t=31时的点:
- 我们分别在 b 0 b 1 b_0 b_1 b0b1上和 b 1 b 2 b_1b_2 b1b2上找到位于 1 3 \frac{1}{3} 31位置的点,分别设为 b 0 1 b_{0}^1 b01和 b 1 1 b_{1}^{1} b11。
- 将这两个点连接起来。
- 在 b 0 1 b_{0}^1 b01和 b 1 1 b_{1}^{1} b11之间再找到位于 1 3 \frac{1}{3} 31位置的点。
- 那么这个点就是贝塞尔曲面在时间 t t t定义的点。
如果我们要画出曲线,我们只需要枚举时间 t t t即可。
这是一个递归的算法。
给定四个控制点的贝塞尔曲线做法也同理:
Evaluating Bezier Curves Algebraic Formula(贝塞尔曲线的代数表示)
例子:二次贝塞尔曲线
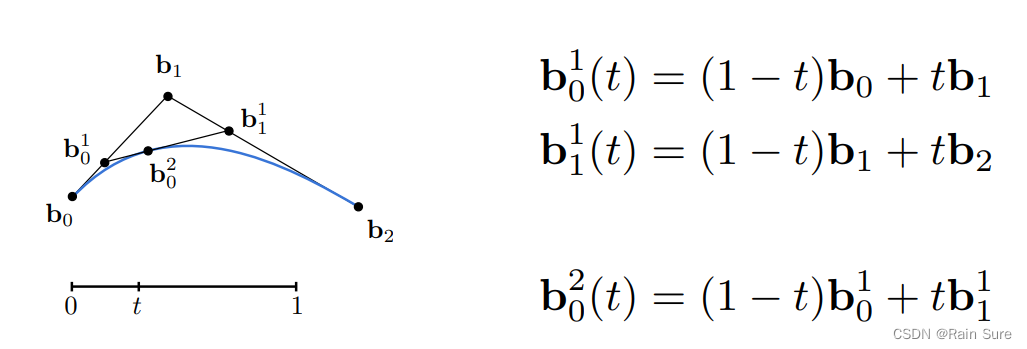
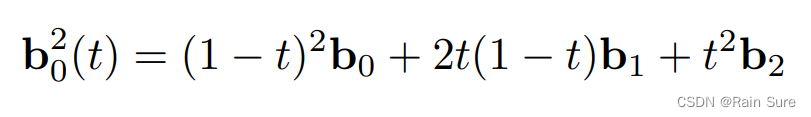
总结一下:
给定
n
+
1
n + 1
n+1个控制点,可以得到
n
n
n阶贝塞尔曲线:
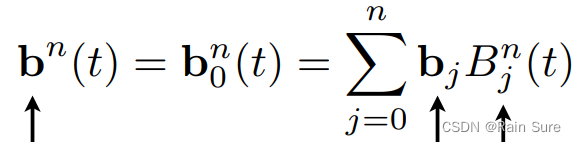
其中,下图中的多项式就是伯恩斯坦多项式。
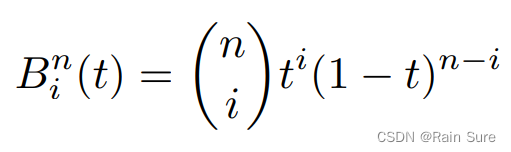
Properties of Bezier Curves(贝塞尔曲线的性质)
- 一定过起止点。
- 起点和终点切线方向一定沿初始方向。
- 在仿射变换下,直接对各个顶点做仿射变换后再画出一条贝塞尔曲线等价于直接对原始贝塞尔曲线做仿射变换。
- 曲线一定在控制点的凸包内。
Piecewise Bezier Curves(分段的贝塞尔曲线)
考虑高阶贝塞尔曲线,可能会出现不符合实际情况的曲线:
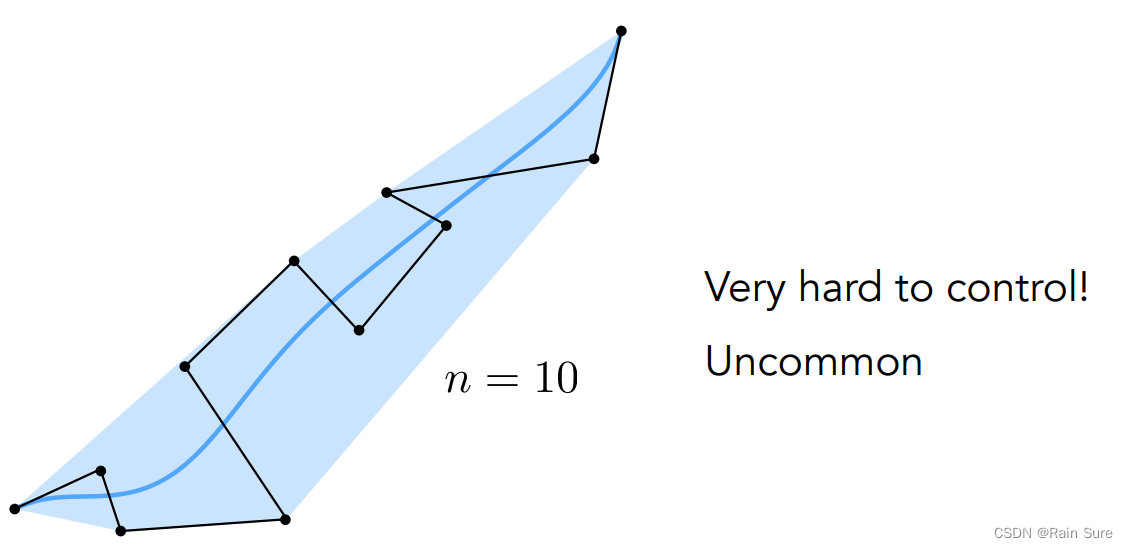
我们可以通过拼接一些低阶贝塞尔曲线来解决这个问题:

Piecewise Bezier Curve - Continuity(分段贝塞尔曲线的连续性)
- C 0 C^{0} C0连续: a n = b 0 a_n = b_0 an=b0第一段的终点等于第二段的起点。
- C 1 C^{1} C1连续: a n = b 0 = 1 2 ( a n − 1 + b 1 ) a_n = b_0 = \frac{1}{2}(a_{n - 1} + b_1) an=b0=21(an−1+b1)切线连续。
- C 2 C^{2} C2连续,曲率连续。
Other types of splines(其它种类的样条)
样条:
穿过一系列给定的点,并有一定数量的连续导数。
简而言之,一个可控的曲线。

B样条:

Surfaces(曲面)
Bezier Surfaces(贝塞尔曲面)

参考
GAMES101 Lecture11