先做一个声明:文章是由我的个人公众号中的推送直接复制粘贴而来,因此对智能优化算法感兴趣的朋友,可关注我的个人公众号:启发式算法讨论。我会不定期在公众号里分享不同的智能优化算法,经典的,或者是近几年提出的新型智能优化算法,并附MATLAB代码。
水母搜索(Jellyfish Search, JS)算法是于2021年提出的一种新型群智能优化算法。水母搜索行为的模拟包括它们的洋流跟随,它们在水母群中的运动(主动运动和被动运动),以及在这些运动之间切换的时间控制机制。作者使用了一套综合的Benchmark函数进行测试,并应用于一系列工程结构问题。相比于其他启发式算法,JS不仅表现最好,而且需要最少的目标函数评估,具有寻优能力强,收敛速度快等特点。
“Chou J S, Truong D N. A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean[J]. Applied Mathematics and Computation, 2021, 389: 125535.”

01
灵感来源
水母生活在世界上不同深度和温度的水中。它们酷似钟状,一些水母的直径小于1cm。它们有各种各样的颜色、大小和形状。大多数水母偏好海洋环境。它们进食的方式有两种:1.利用触手把食物送进嘴里;2.以触手过滤水中的微小的浮游生物,经口腕沟靠纤毛作用送入口。它们捕食方式也有两种:1.食用洋流带来的任何食物(被动);2.主动捕食猎物,利用触手刺中猎物,令其动弹不得(主动),如图1所示。

图1 水母利用触手捕食猎物
水母可以自己控制移动。它们下侧像一把伞一样合拢,利用体内喷水反射前进。尽管它们拥有这种能力,但是它们大多数漂流在水中依靠洋流和潮汐运动。当条件有利时,水母会形成群,这种被称为水母潮(Jellyfifish Bloom)。水母是一种脆弱的生物,维持水母潮的关键是它们相对洋流的方向,才不至于被搁浅。
水母自身的运动和洋流的运动促成了水母潮的形成,这种现象在海洋中随处可见。水母去的地方,食物数量各不相同。因此,通过食物比例的比较,确定最佳位置。作者以水母在海洋中的搜索行为和运动为灵感,提出了JS算法。图2给出了算法的大致步骤。
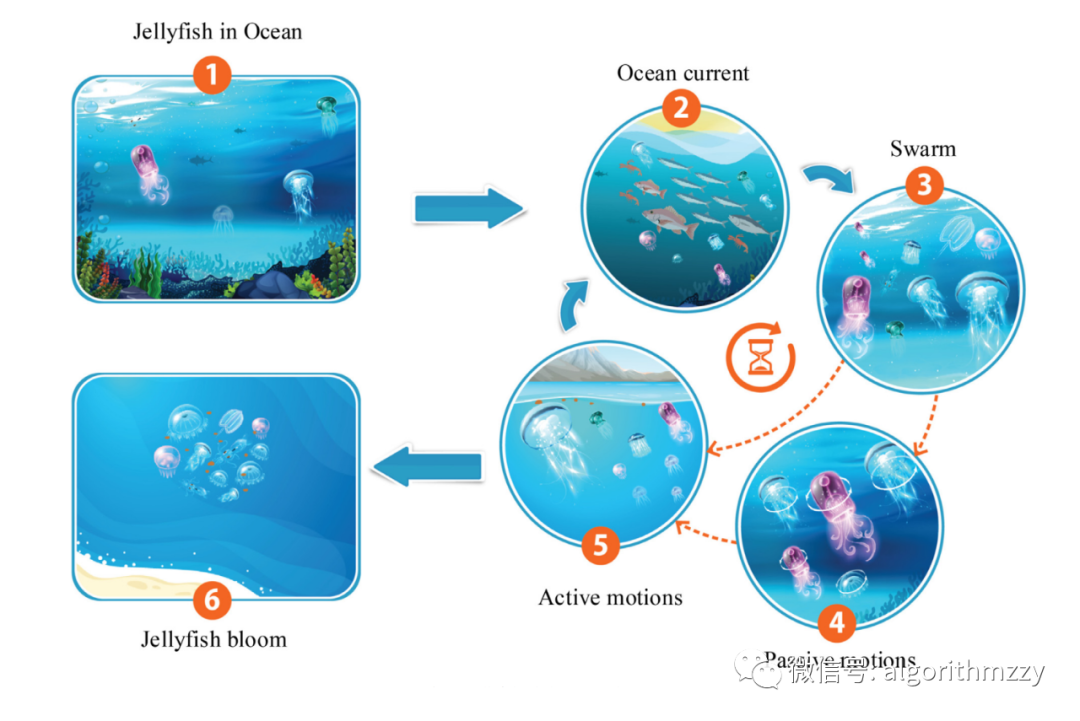
图2 水母在海洋中的种群行为
02
算法设计
水母搜索算法通过模拟水母跟随洋流和在种群内部的运动方式(主动运动和被动运动),以及在这些运动之间切换的时间控制机制来建立数学模型。
首先,JS算法的三个理想化规则(模型假设):
1.水母要么跟随洋流,要么在群内自身移动,这两者运动由时间控制机制切换;
2.在海洋中,水母寻找食物时,它们会被食物数量更多的位置吸引;
3.找到的食物数量由该位置和对应的目标函数决定。
在这三条准则的基础上,JS算法的描述如下:


03
计算流程
JS算法的计算流程图如图3所示:
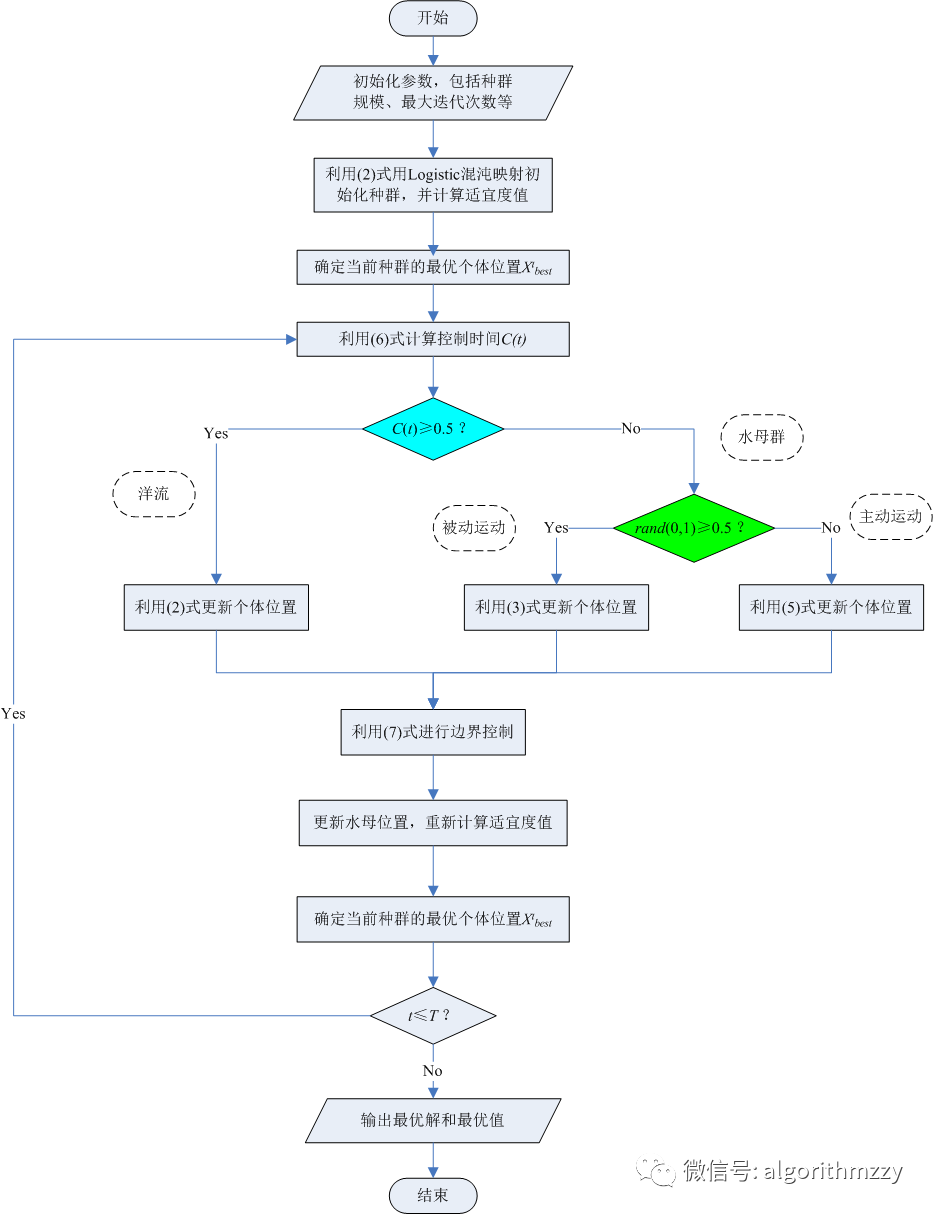
图3 JS的计算流程
04
实验仿真
这里对JS算法的性能进行简单的测试。首先将JS用于函数寻优,算法的MATLAB程序是严格按照它的原始参考文献进行编码的。此外,种群规模取N等于50,Benchmark函数分别采用了CEC2005测试集、CEC2013测试集、CEC2014测试集、CEC2017测试集和CEC2020优化函数测试集。这里对仿真结果进行简要展示,就不再进一步做分析了。
首先,我们来检验一下JS算法对全局勘探和局部开发的平衡能力。如图4所示,是JS算法在CEC2005测试函数f7上的勘探和开发占比曲线。
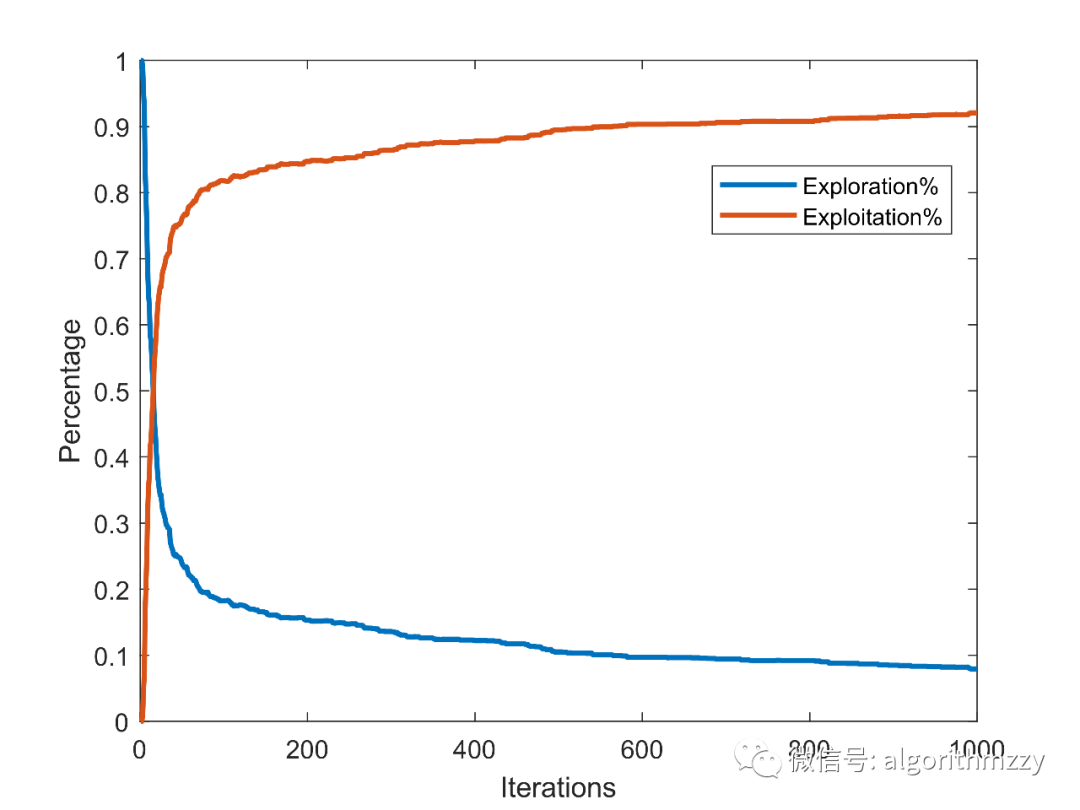
图4 JS在CEC2005 f7上的勘探和开发百分占比变化曲线
其次,以CEC2005的多峰函数Ackley (f10)为例,展示JS算法在30维环境下的收敛效果。在之前我还推送过几期海洋中的其他动物算法,如:鲸鱼优化算法(WOA)及其优秀变体(含MATLAB代码)、樽海鞘群算法(SSA)(含MATLAB代码)、旗鱼优化(SFO)算法(含MATLAB代码)、䲟鱼优化算法(ROA)(含MATLAB代码)、白鲸优化(BWO)算法(含MATLAB代码)
将它们作为对比算法,看看谁才是“海洋一哥”!最大迭代次数T均设为1000,比较它们的收敛性能,如图5所示。
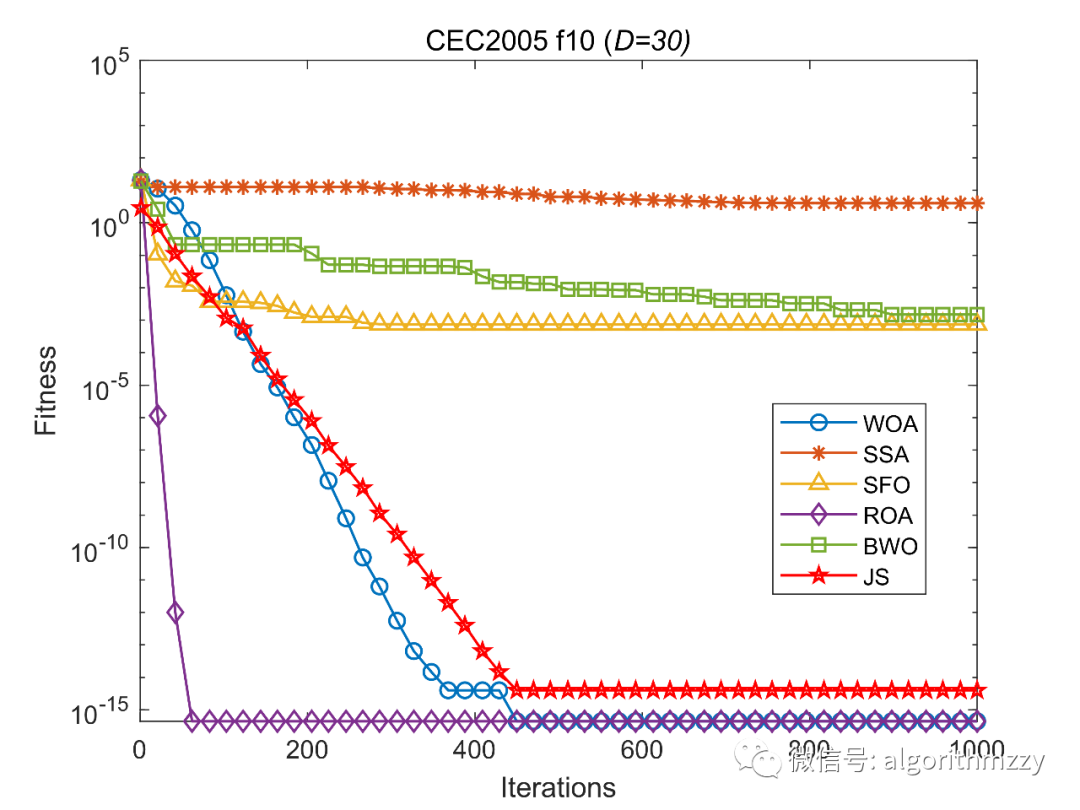
图5 六种对比算法在CEC2005 f10上的收敛曲线
再次,以CEC2013测试集中的单峰函数F5为例,展示JS算法在30维环境下的收敛效果,如图6所示。(注意是画的误差曲线)
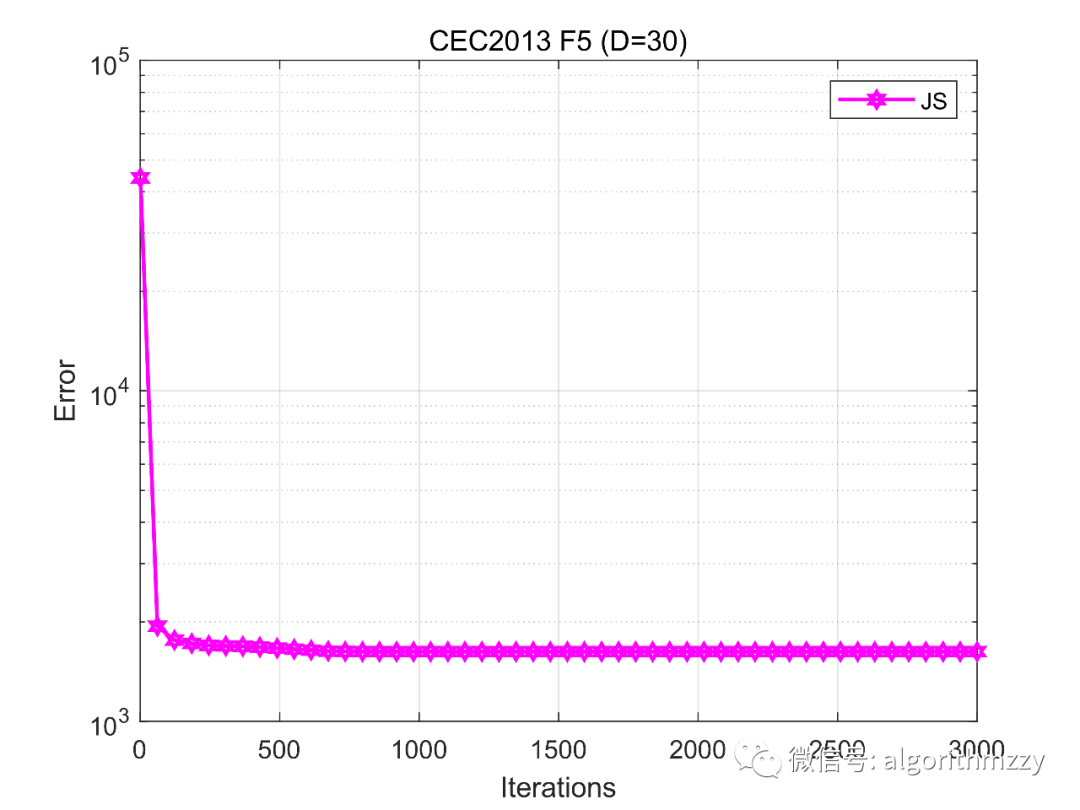
图6 JS在CEC2013 F5上的误差收敛曲线
接着,以CEC2014测试集中的混合函数F19为例,展示JS算法在30维环境下的收敛效果,如图7所示。(注意是画的误差曲线)
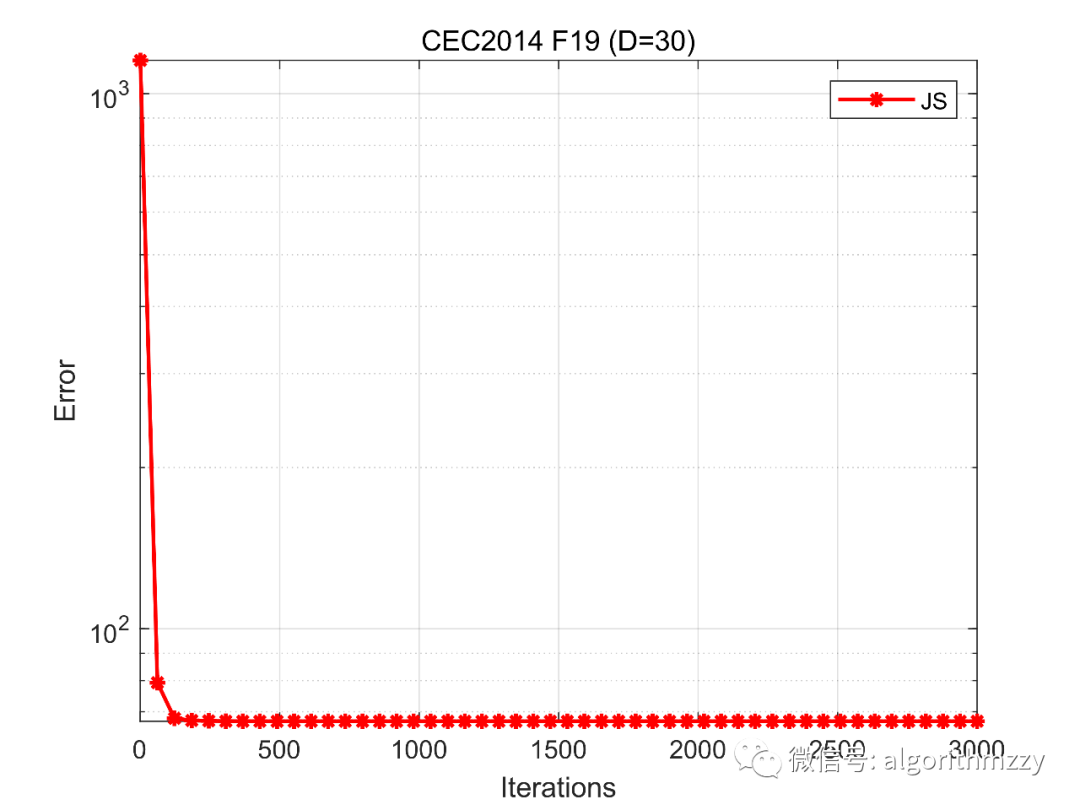
图7 JS在CEC2014 F19上的误差收敛曲线
再然后,以CEC2017测试集中的多模态函数F4为例,展示JS算法在30维环境下的收敛效果,如图8所示。(注意是画的误差曲线)
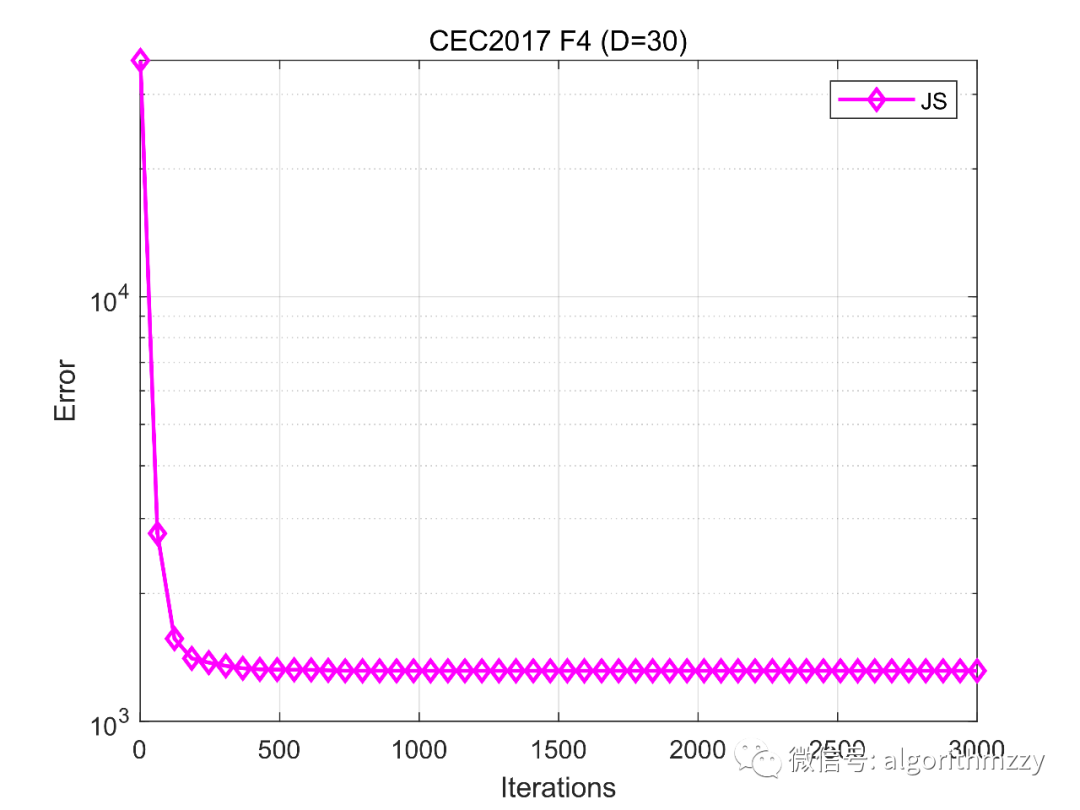
图8 JS在CEC2017 F4上的误差收敛曲线
最后,以CEC2020优化函数测试集中的复合函数F9为例,展示JS算法在10维环境下的收敛效果,如图9所示。(注意是画的误差曲线)
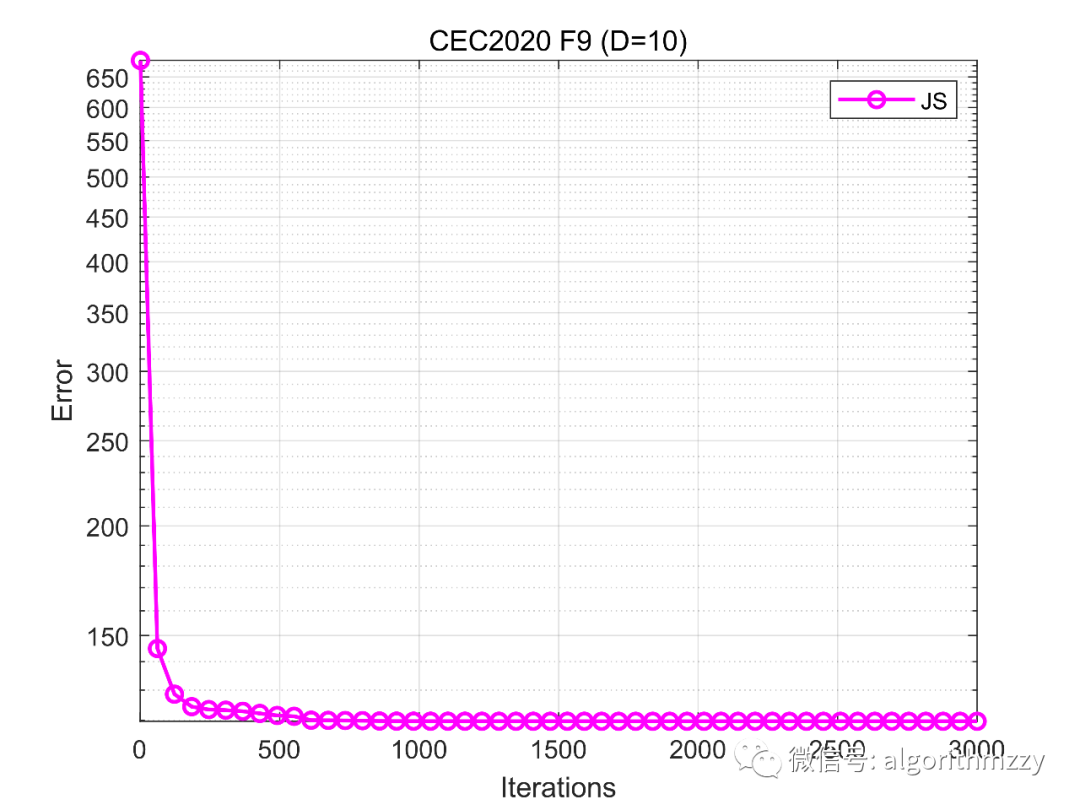
图9 JS在CEC2020优化函数 F9上的误差收敛曲线
进一步,可将JS算法应用于复杂工程约束优化问题,例如之前推送的两期算法应用内容:
算法应用:基于DBO算法的工程优化设计(第1期)(含MATLAB代码)
算法应用:工程优化设计(第2期)(含MATLAB代码)
这里以压力容器设计(Pressure vessel design)问题为例,展示JS算法求解效果。对比算法选择:灰狼优化(GWO)、哈里斯鹰优化(HHO)、沙猫群优化(SCSO)、蜣螂优化(DBO)、浣熊优化(COA)。收敛曲线如图10所示。
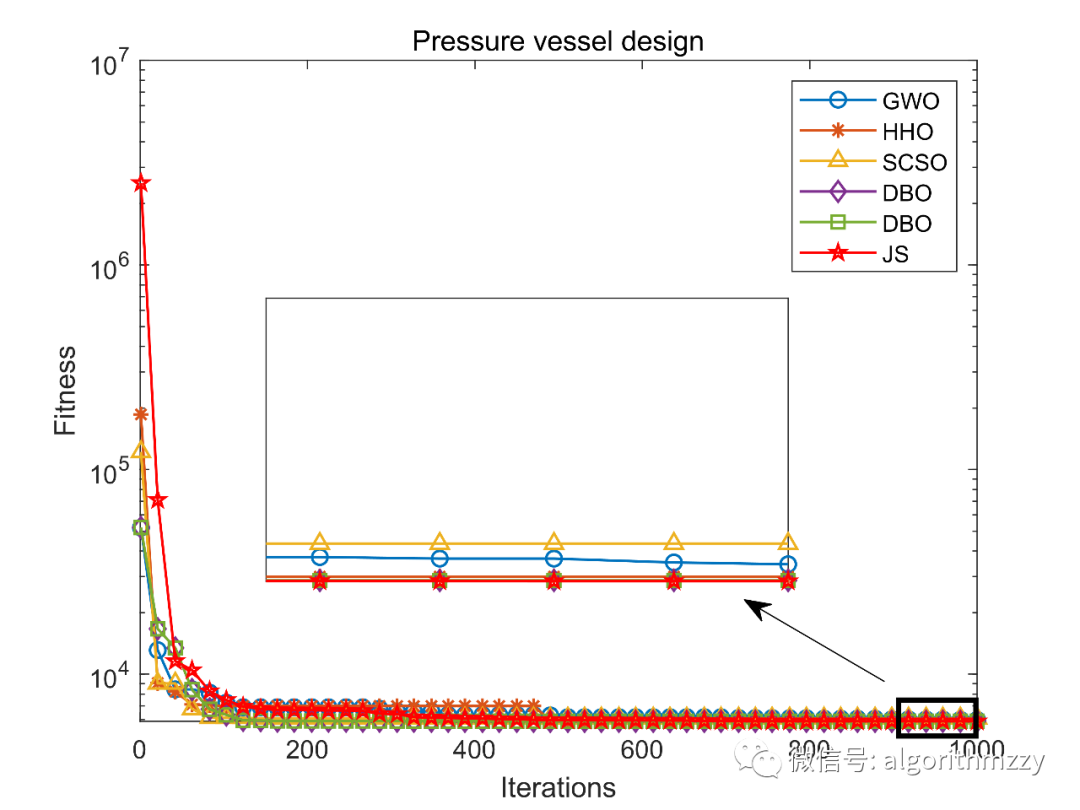
图10 六种对比算法在压力容器设计问题上的目标函数收敛曲线
05
MATLAB代码
公众号里有,关注:启发式算法讨论