题目:

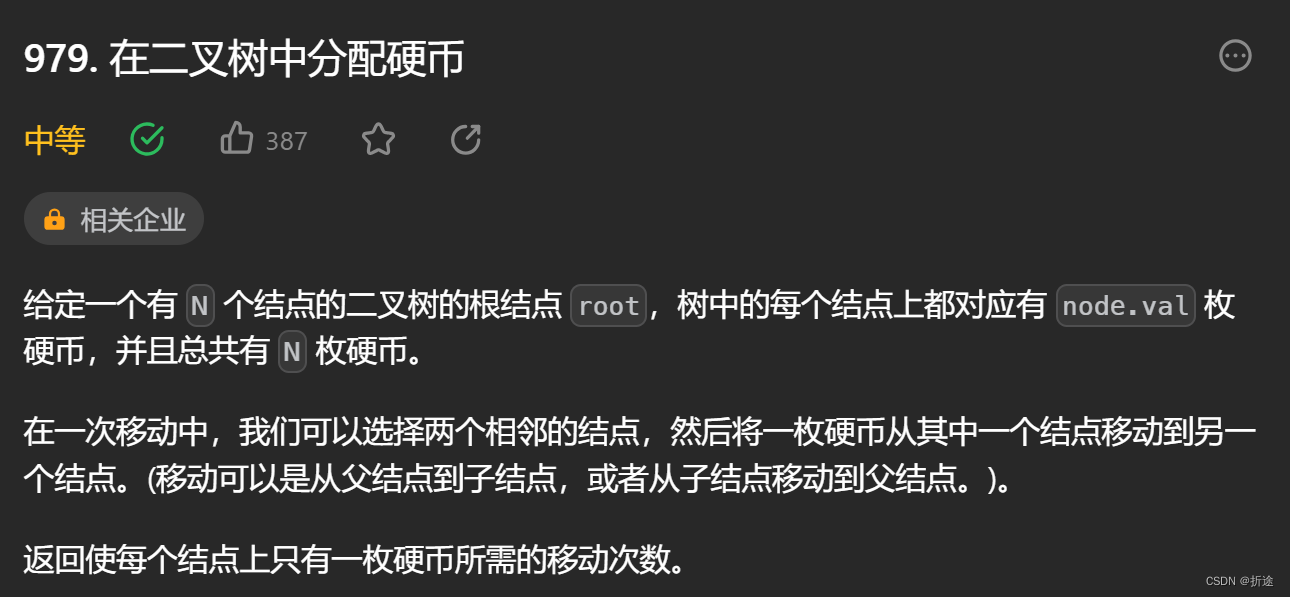
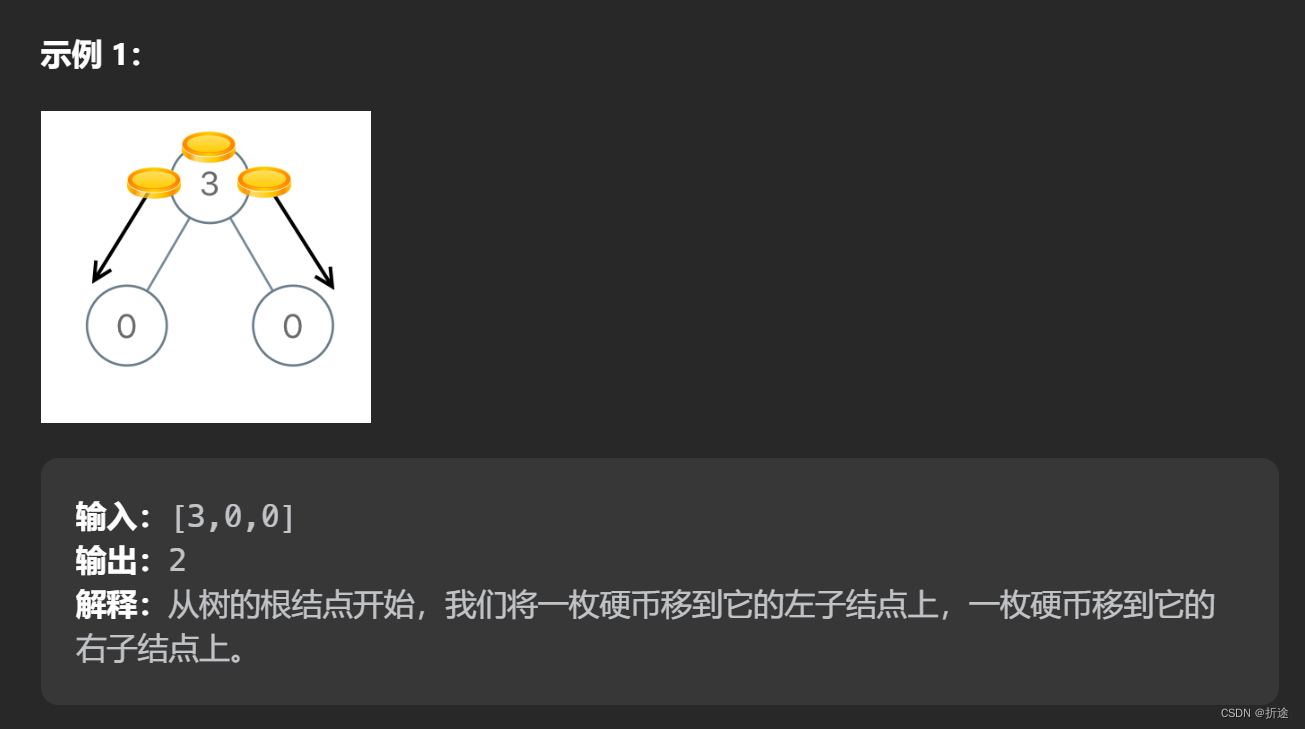
示例:

分析:

给一个二叉树,二叉树的值总和等于整个二叉树的节点数,我们一次可以移动一个节点的一个值到相邻节点,问我们需要移动多少次才可以把值的总和平均分配每个节点(即每个节点的值都为1).

我们可以确定的是,如果某个节点的左子树共有n个节点,而节点值总和为m,那么光这个节点的左子树就会有|n-m|个值会经过这个节点,我们虽然不知道|n-m|个值一共要移动多少次,但是光是与节点相邻的边就一定会要移动|n-m|次.以示例1为例,我们结合下图来说明一下:

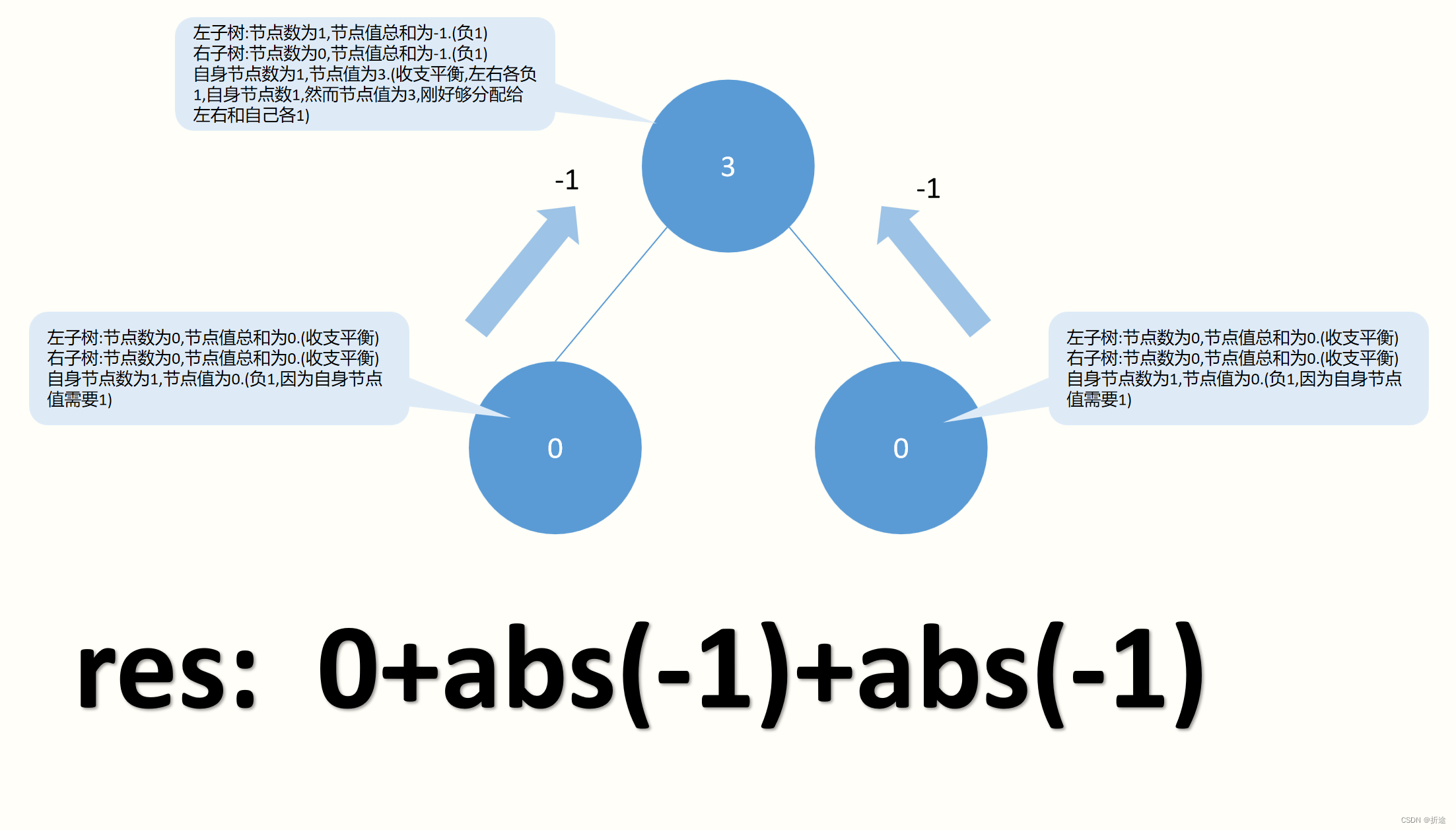
 以根节点的左节点为例,它没有左右子树,也就是说子树节点和为0,子树节点值总和也为0,二者相同,可以暂时不用管.而自己的值为0,但是自己需要有一个值,那也就只能从父节点给一个值过来,所以左节点和根节点之间的这条路径,会有一个值传递过来,也就是算作移动一次(即使还没有发生,但是我们可以预料到会发生,因此可以先加入到res中).

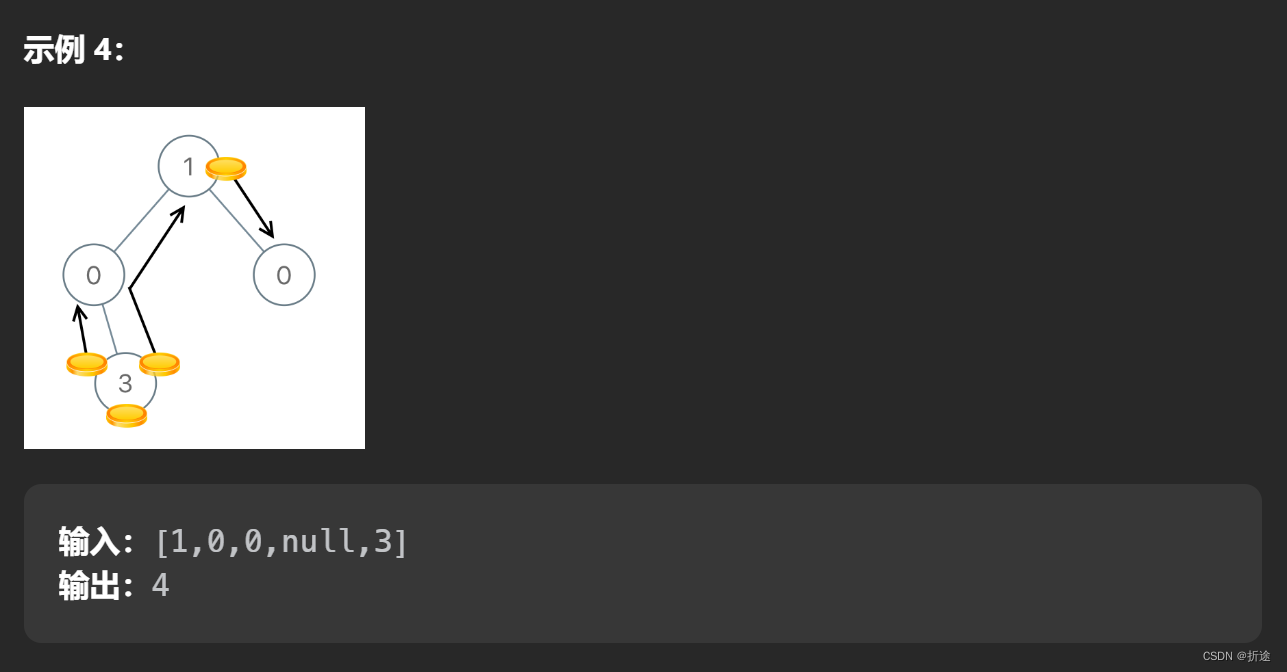
我们再看一下示例四:

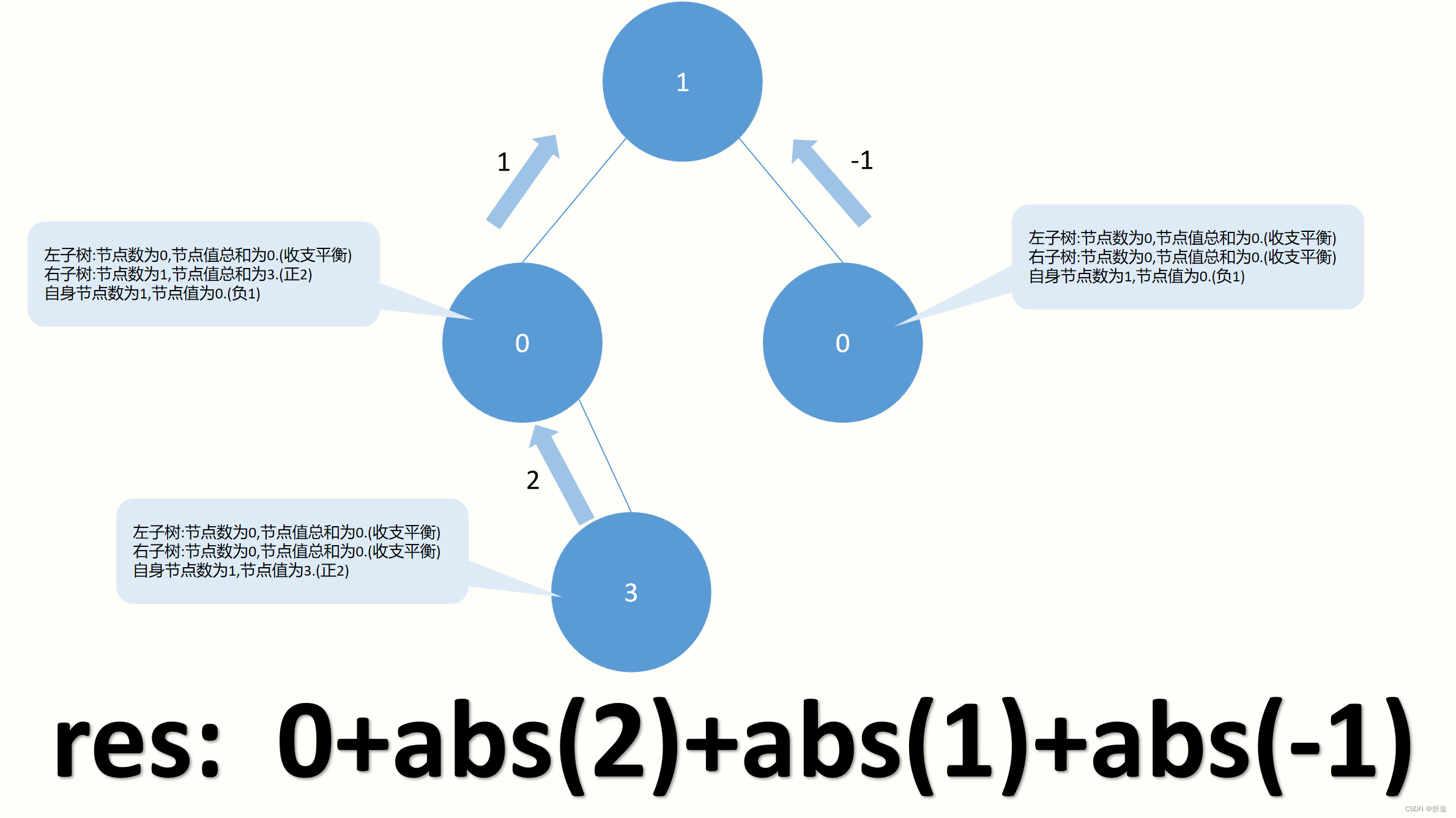
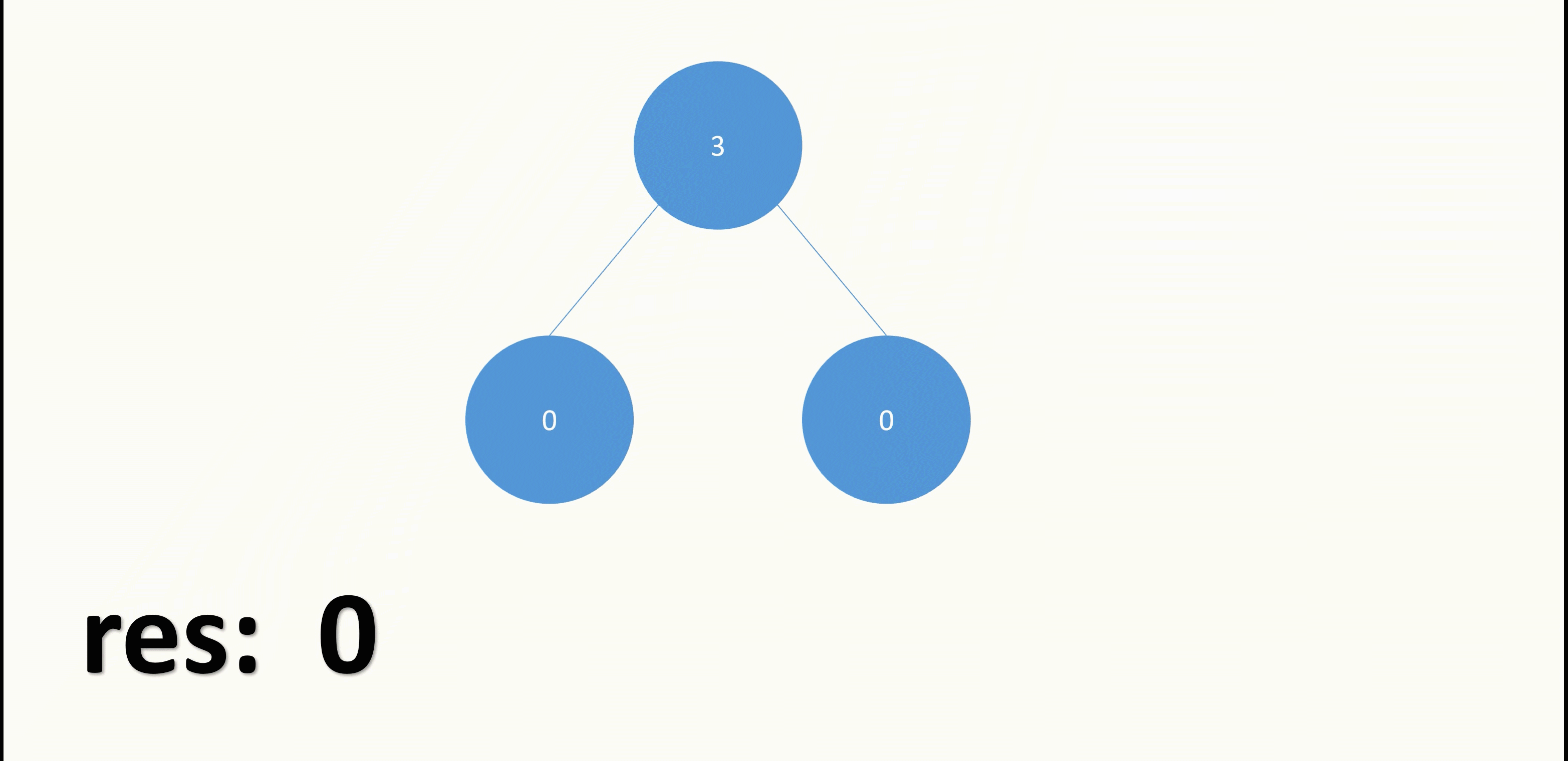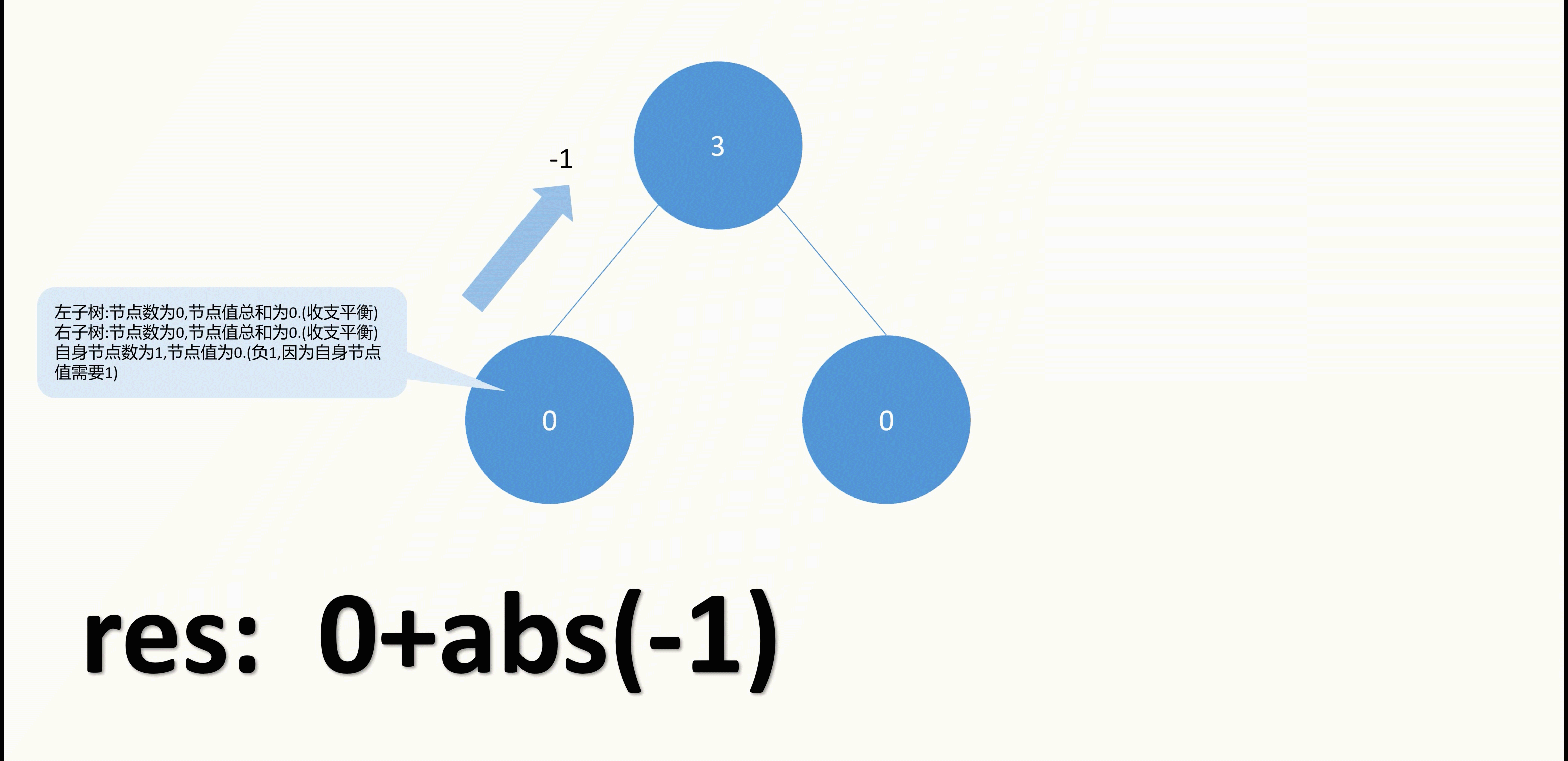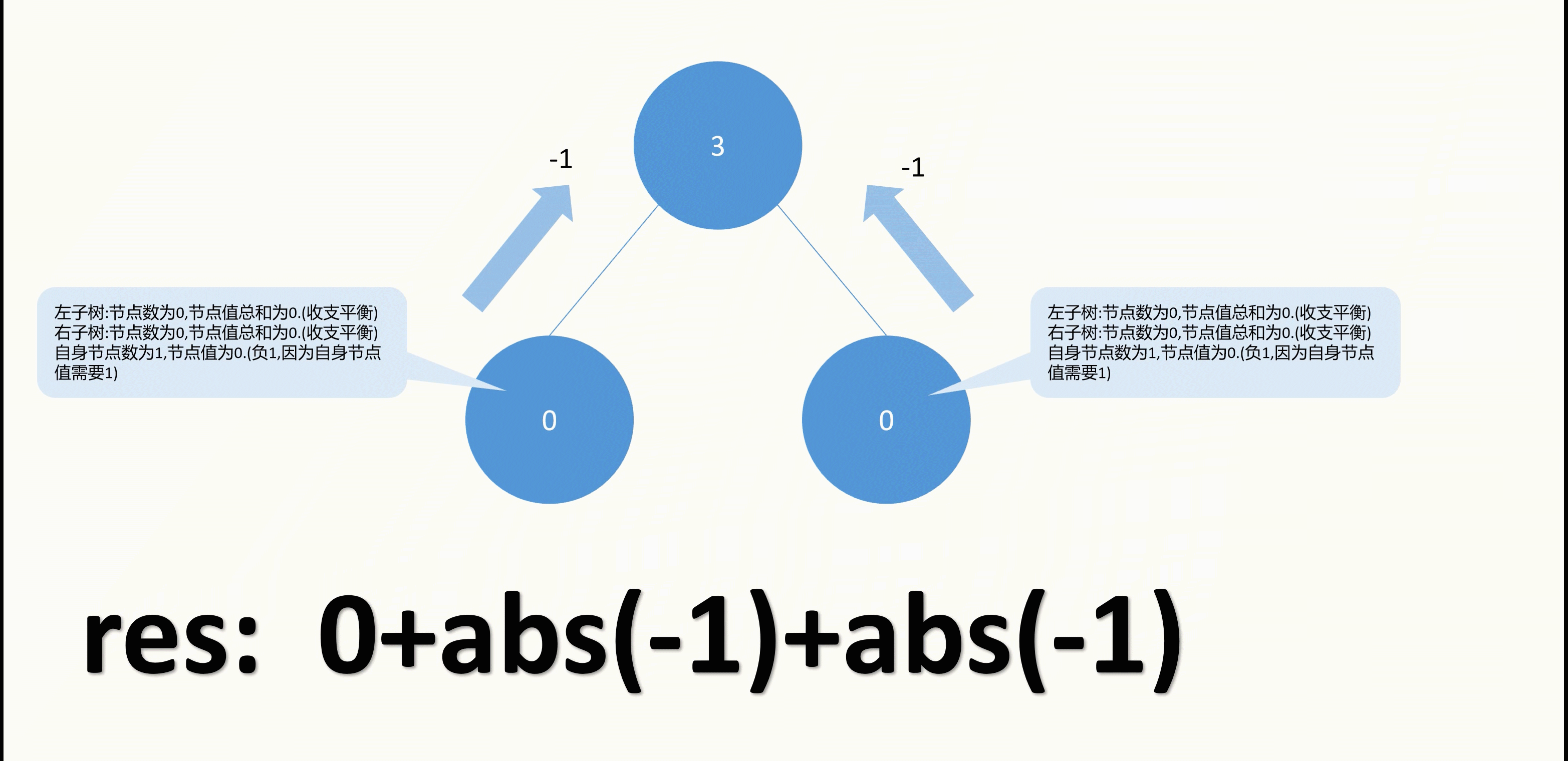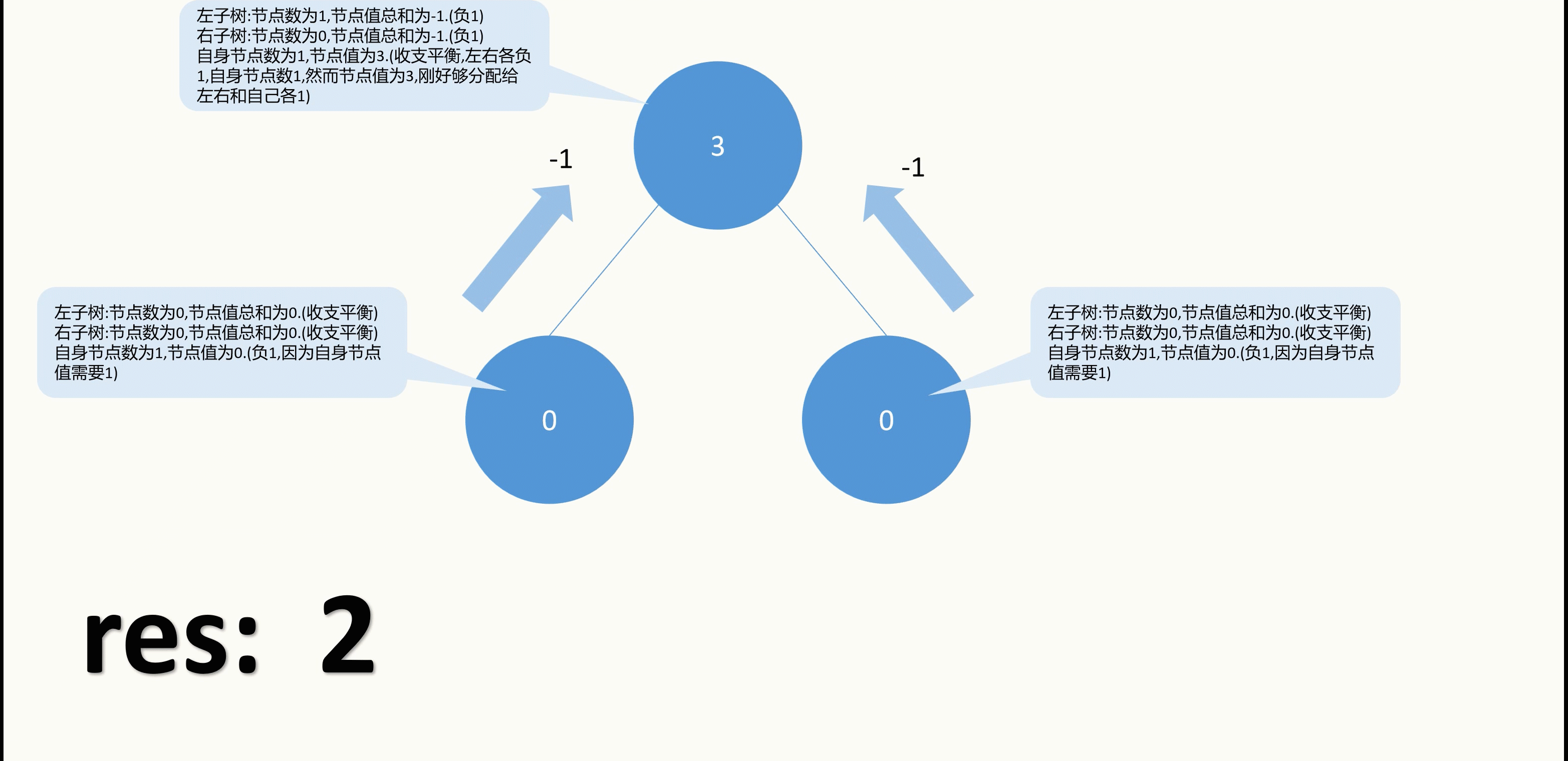
 最下面的值为3的节点,没有子树,自然也没有子树值总和,因此在子树这方面属于收支平衡,而自己的节点值为3,比1多2,因此它必须把两个值都传递给父节点,所以算是需要传递两次(res+=abs(2)).

再看一下左边的值为0的节点,该节点的子树节点数为1,而子树节点值总和为3,有2的盈余,但是自己的值为0,算是自身亏损1,再加上子树的盈余,因此总的有1的盈余,因此它必然有一个值要传递给它的父节点,所以算是要传递一次(res+=abs(1)).

再复杂的二叉树也是如此分析的,因此我们可以总结出一个套路,就是遍历二叉树,然后找出节点的节点数和值总和,再算上自己的值减1(自己节点数为1)传递给父节点,并且取绝对值后加入到结果中.

完整代码+结果如下:

class Solution {
public:
    int res=0;
    int dfs(TreeNode* root){
        if(root==nullptr) return 0;
        int need=dfs(root->left)+dfs(root->right)+root->val-1;
        res+=abs(need);
        return need;
    }


    int distributeCoins(TreeNode* root) {
        dfs(root);
        return res;
    }
};