目录

1 神经元

2 MP模型

3 激活函数

      3.1 激活函数

      3.2 激活函数作用

      3.3 激活函数有多种

4、神经网络模型

---

1 神经元

       神经元是主要由树突、轴突、突出组成，树突是从上面接收很多信号，经过轴突处理后传递给突触，突触会进行选择性向下一级的树突传递信号。突触输出的信号只有两种可能，要么输出，要么不输出，即只有0和1两种情况。

       在生物神经网络中，每个神经元与其他神经元相连，当它“兴奋”时，就会向相连的神经元发送化学物质，从而改变这些神经元内的电位；如果某神经元的电位超过了一个“阈值”，那么它就会被激活，即“兴奋”起来，向其他神经元发送化学物质。

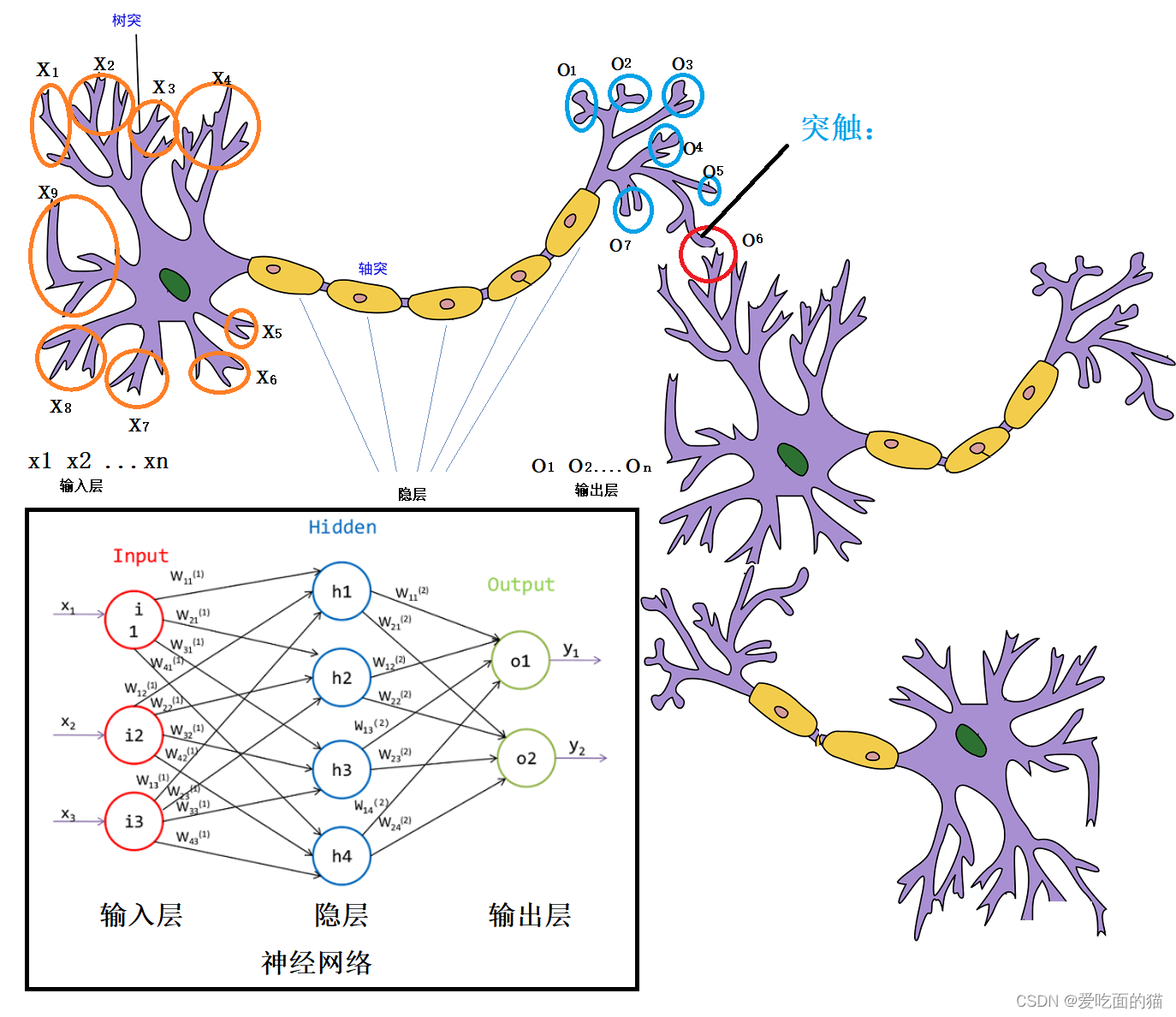
2 MP模型

       每个神经网络单元抽象出来的数学MP模型如下，也叫感知器，它接收多个输入（x1，x2，x3...），产生一个输出 即 y= W1X1+W2X2+W3X3+...+WnXn + b。

       这就好比是神经末梢感受各种外部环境的变化（感知外部刺激），产生不同的电信号（也就是输入：x1，x2，x3...xn），这些强度不同(也就是参数w1,w2,w3...wn)的电信号汇聚到一起，会改变这些神经元内的电位，如果神经元的电位超过了一个“阈值”（参数 b），它就会被激活(激活函数)，即“兴奋”起来，向其他神经元发送化学物质。

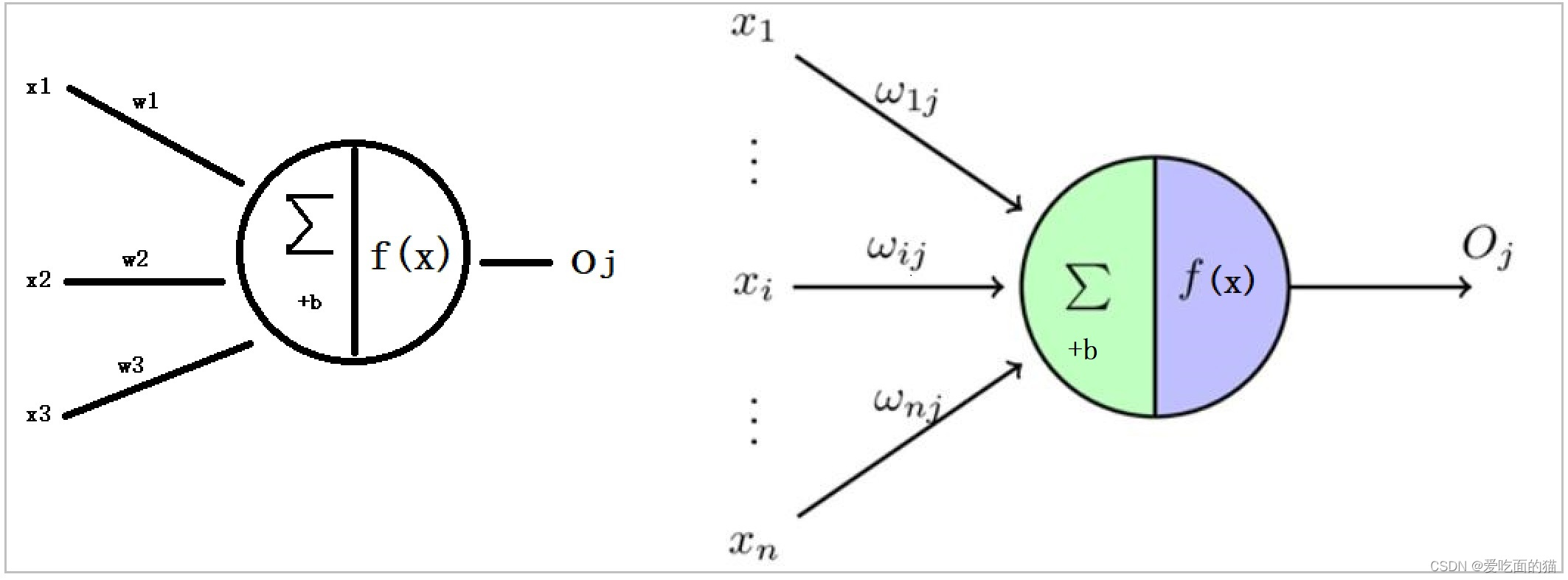
        MP模型：麦卡洛克一皮茨模型(McCulloch-Pitts model )简称，一种早期的神经元网络模型.

       由美国神经生理学家麦卡洛克(McCulloch, W.)和数学家皮茨 <Pitts,W.)于1943年共同提出。设有n个神经元相互连结，每个神经元的状态Si (i=1，2，…，n)取值0或1，分别表示该神经元的抑制和兴奋，每个神经元的状态都受其他神经元的制约，B是第i个神经元的阂值，W是神经元i与神经元J 之间的连结强度。

MP模型过程：

• 每个神经元都是一个多输入端
• 如x1,x2,x3
• 每个输入都会乘以权重w1,w2,w3
• 再加一个阈值 b
• 最后我们会得到 y = w1x1 + w2x2 + w3x3 + b
• 最终我们得到一个值 y
• 得到这个值后是否会向下游输出则取决于激活函数f(x)
• 向下游输出的结果Oj的值要么是0，要么是1。

3 激活函数

      3.1 激活函数

        就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。

      3.2 激活函数作用

       如果不用激活函数：每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机（Perceptron）。
        如果使用激活函数：激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

      3.3 激活函数有多种

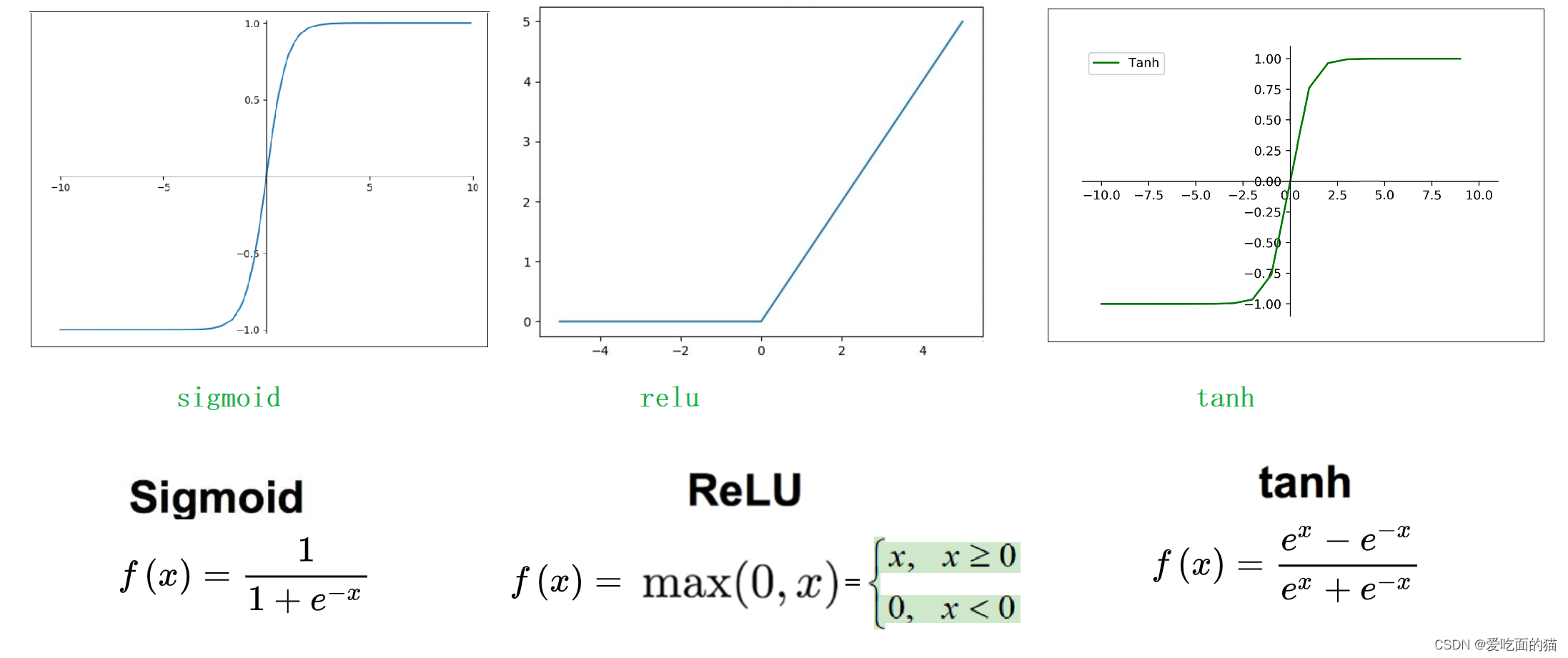
• Sigmoid激活函数

        Sigmoid函数是一个在生物学中常见的S型函数，也称为S型生长曲线。在信息科学中，由于其单增以及反函数单增等性质，Sigmoid函数常被用作神经网络的阈值函数，将变量映射到0,1之间 。

• ReLU函数

       Relu激活函数（The Rectified Linear Unit），用于隐层神经元输出。

• Tanh函数

       Tanh是双曲函数中的一个，Tanh()为双曲正切。在数学中，双曲正切“Tanh”是由基本双曲函数双曲正弦和双曲余弦推导而来。

4、神经网络模型

       单个的感知器(也叫单感知机)就构成了一个简单的模型(MP模型)，但在现实世界中，实际的决策模型则要复杂得多，往往是由多个感知器组成的多层网络，如下图所示，这也是经典的神经网络模型（也叫多感知机），由输入层、隐含层、输出层构成。

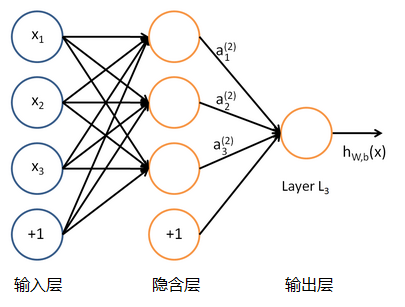
       人工神经网络可以映射任意复杂的非线性关系，具有很强的鲁棒性、记忆能力、自学习等能力，在分类、预测、模式识别等方面有着广泛的应用。