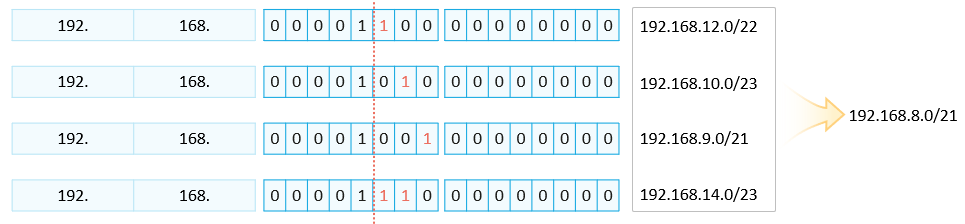
张量和随机运行,exp函数
import torch
a = torch.tensor([[1,2],[3,4]])
print(a)
a = torch.randn(size=(10,3))
print(a)
b = a-a[0]
print(torch.exp(b)[0].numpy())
输出:
tensor([[1, 2],
[3, 4]])
tensor([[-1.0165, 0.3531, -0.0852],
[-0.1065, -0.5012, 0.8104],
[-2.1894, -0.1413, -0.6508],
[-0.1741, 0.3935, 1.1463],
[-0.2633, 0.3840, 0.9641],
[ 0.3000, -0.1504, 0.9952],
[ 1.5889, 1.0660, 0.3868],
[ 0.9958, -0.6398, -0.5993],
[-0.3170, -3.0703, 0.5259],
[ 0.2989, -0.6463, -0.8022]])
[1. 1. 1.]
a-a[0] ,也就意味着所有的行减去第一行,这样b的第一行就是[0,0,0], ===>exp(0)= 1 所以
torch.exp(b)[0].numpy 都是1.
计算梯度
什么是梯度呢,梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。为什么要这个变化率最大的呢?其实就是变化最大的地方就是特征,理解了吧。我们在pytorch里面用以下函数来求解梯度,并反向传播
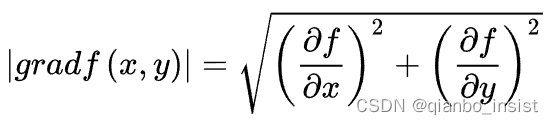
import torch
a = torch.randn(size=(2, 2), requires_grad=True)
b = torch.randn(size=(2, 2))
c = torch.mean(torch.sqrt(torch.square(a) + torch.square(b))) # Do some math using `a`
c.backward() # call backward() to compute all gradients
print(a.grad)
如果将张量的属性 .requires_grad 设置为 True ,它将开始追踪(track)在其上的所有操作,可以利⽤链式法则进⾏梯度传播了。完成计算后,可以调 ⽤ .backward() 来完成所有梯度计算,并且 Tensor 的梯度将累积到 .grad 属性中。backward() 时,如果 x 是标量,则不需要为 backward() 传⼊任何参数;否则,需要传⼊⼀个与 x 同形的 Tensor 。
pytorch会自动累计梯度运算,通过zero_() 函数可以清除累计
a = torch.tensor([[1.2,2.1],[3.0,4.1]],requires_grad=True);
b = torch.tensor([[5,6],[7,8]]);
c = torch.mean(torch.sqrt(torch.square(a) + torch.square(b)))
c.backward(retain_graph=True)
print(a.grad)
c.backward(retain_graph=True)
print(a.grad)
a.grad.zero_()
c.backward()
print(a.grad)
打印
tensor([[0.0583, 0.0826],
[0.0985, 0.1140]])
tensor([[0.1167, 0.1652],
[0.1970, 0.2280]])
tensor([[0.0583, 0.0826],
[0.0985, 0.1140]])
zero_() 操作以后,梯度运算又恢复了
pytorch 计算标量函数的梯度,相当于损失函数,计算一个张量对于另外一个张量的梯度,我们需要一个雅可比矩阵和一个给定的向量,假定我们有一个向量函数 y = f(x) , y = [y1,y2,y3,y4,…yn] , 那 y关于 x 的梯度 被定义为一个雅可比矩阵,就是每个y 量对于x 的求导,如下图所示
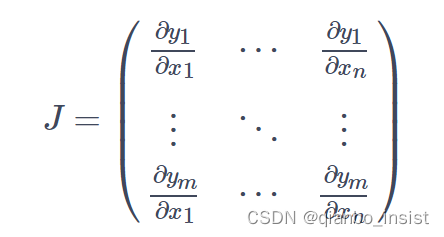
pytorch里面会计算每个的乘积。
梯度下降的优化
看以下这个函数,先定义全 0 矩阵,再定义一个函数f
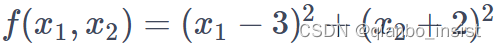
我们使用lambda 来定义一个函数,lambda x 代表每一个x的值,我们都做定义
x = torch.zeros(2,requires_grad=True)
f = lambda x : (x-torch.tensor([3,-2])).pow(2).sum()
lr = 0.1
我们求解15次迭代进行梯度下降, 每次迭代, 我们更新x ,同时打印一下,确保我们接近我们需要的点在(3,-2)附近,lr实际上就是我们学习的学习率
for i in range(15):
y = f(x)
y.backward()
gr = x.grad
x.data.add_(-lr*gr)
x.grad.zero_()
print("Step {}: x[0]={}, x[1]={}".format(i,x[0],x[1]))
打印如下值
Step 0: x[0]=0.6000000238418579, x[1]=-0.4000000059604645
Step 1: x[0]=1.0800000429153442, x[1]=-0.7200000286102295
Step 2: x[0]=1.4639999866485596, x[1]=-0.9760000705718994
Step 3: x[0]=1.7711999416351318, x[1]=-1.1808000802993774
Step 4: x[0]=2.0169599056243896, x[1]=-1.3446400165557861
Step 5: x[0]=2.2135679721832275, x[1]=-1.4757120609283447
Step 6: x[0]=2.370854377746582, x[1]=-1.5805696249008179
Step 7: x[0]=2.4966835975646973, x[1]=-1.6644556522369385
Step 8: x[0]=2.597346782684326, x[1]=-1.7315645217895508
Step 9: x[0]=2.677877426147461, x[1]=-1.7852516174316406
Step 10: x[0]=2.7423019409179688, x[1]=-1.8282012939453125
Step 11: x[0]=2.793841600418091, x[1]=-1.8625609874725342
Step 12: x[0]=2.835073232650757, x[1]=-1.8900487422943115
Step 13: x[0]=2.868058681488037, x[1]=-1.912039041519165
Step 14: x[0]=2.894446849822998, x[1]=-1.929631233215332
是不是慢慢开始理解梯度了
线性回归
先看下面这个例子,我们使用scikit-learn 包来使用线性回归。如果没有安装,请使用如下命令
pip install scikit-learn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification, make_regression
from sklearn.model_selection import train_test_split
import random
np.random.seed(13) # pick the seed for reproducibility - change it to explore the effects of random variations
train_x = np.linspace(0, 3, 120)
train_labels = 2 * train_x + 0.9 + np.random.randn(*train_x.shape) * 0.5
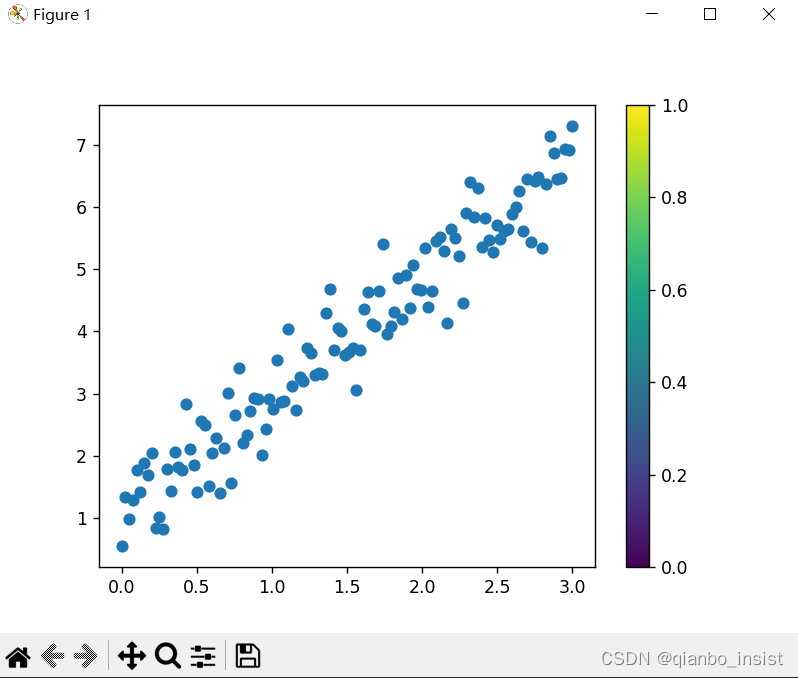
plt.scatter(train_x,train_labels)
plt.colorbar() # 显示颜色条
plt.show()
显示如下图,我们能生成了等差数列,得到了一些数据
我们来定义模型和损失函数
input_dim = 1
output_dim = 1
learning_rate = 0.1
# 权重 y = wx + b, b 就是模型参数
w = torch.tensor([100.0],requires_grad=True,dtype=torch.float32)
# bias 向量
b = torch.zeros(size=(output_dim,),requires_grad=True)
def f(x):
return torch.matmul(x,w) + b
# 定义计算损失函数
def compute_loss(labels, predictions):
return torch.mean(torch.square(labels - predictions))
定义训练的过程函数
def train_on_batch(x, y):
predictions = f(x)
loss = compute_loss(y, predictions)
loss.backward()
w.data.sub_(learning_rate * w.grad)
b.data.sub_(learning_rate * b.grad)
w.grad.zero_()
b.grad.zero_()
return loss
打乱数据
indices = np.random.permutation(len(train_x))
features = torch.tensor(train_x[indices],dtype=torch.float32)
labels = torch.tensor(train_labels[indices],dtype=torch.float32)
定义批次
batch_size = 4
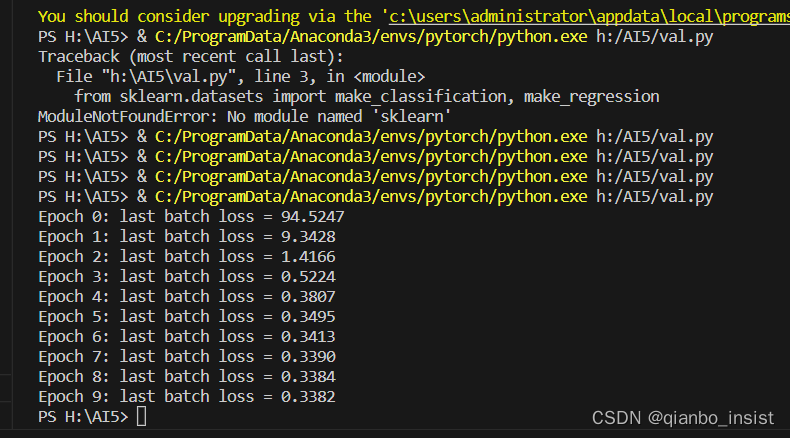
for epoch in range(10):
for i in range(0,len(features),batch_size):
loss = train_on_batch(features[i:i+batch_size].view(-1,1),labels[i:i+batch_size])
print('Epoch %d: last batch loss = %.4f' % (epoch, float(loss)))
打印如下
Epoch 0: last batch loss = 94.5247
Epoch 1: last batch loss = 9.3428
Epoch 2: last batch loss = 1.4166
Epoch 3: last batch loss = 0.5224
Epoch 4: last batch loss = 0.3807
Epoch 5: last batch loss = 0.3495
Epoch 6: last batch loss = 0.3413
Epoch 7: last batch loss = 0.3390
Epoch 8: last batch loss = 0.3384
Epoch 9: last batch loss = 0.3382
不用怀疑,我截图一下,值就是这样,因为我们的数据是等差数列
补充一下,不然就不是线性回归了
print(w,b)
值如下所示
tensor([1.8617], requires_grad=True) tensor([1.0711], requires_grad=True)
解释一下np.random.permutation函数,是一个随机排列函数,就是将输入的数据进行随机排列,生成了120个数据
np.random.permutation(len(train_x))
import torch
import numpy as np
x = np.linspace(0, 3, 120)
print(x)
print(len(x))
indices = np.random.permutation(len(x))
print(indices)
试一下上面这段程序,打印输出:
[0. 0.02521008 0.05042017 0.07563025 0.10084034 0.12605042
0.1512605 0.17647059 0.20168067 0.22689076 0.25210084 0.27731092
0.30252101 0.32773109 0.35294118 0.37815126 0.40336134 0.42857143
0.45378151 0.4789916 0.50420168 0.52941176 0.55462185 0.57983193
0.60504202 0.6302521 0.65546218 0.68067227 0.70588235 0.73109244
0.75630252 0.78151261 0.80672269 0.83193277 0.85714286 0.88235294
0.90756303 0.93277311 0.95798319 0.98319328 1.00840336 1.03361345
1.05882353 1.08403361 1.1092437 1.13445378 1.15966387 1.18487395
1.21008403 1.23529412 1.2605042 1.28571429 1.31092437 1.33613445
1.36134454 1.38655462 1.41176471 1.43697479 1.46218487 1.48739496
1.51260504 1.53781513 1.56302521 1.58823529 1.61344538 1.63865546
1.66386555 1.68907563 1.71428571 1.7394958 1.76470588 1.78991597
1.81512605 1.84033613 1.86554622 1.8907563 1.91596639 1.94117647
1.96638655 1.99159664 2.01680672 2.04201681 2.06722689 2.09243697
2.11764706 2.14285714 2.16806723 2.19327731 2.21848739 2.24369748
2.26890756 2.29411765 2.31932773 2.34453782 2.3697479 2.39495798
2.42016807 2.44537815 2.47058824 2.49579832 2.5210084 2.54621849
2.57142857 2.59663866 2.62184874 2.64705882 2.67226891 2.69747899
2.72268908 2.74789916 2.77310924 2.79831933 2.82352941 2.8487395
2.87394958 2.89915966 2.92436975 2.94957983 2.97478992 3. ]
120
[ 65 58 25 68 47 85 64 111 59 82 96 27 34 24 62 95 100 10
79 78 80 98 41 14 97 108 69 16 92 66 15 106 0 42 81 107
70 91 116 5 94 46 17 11 3 57 35 115 109 8 29 74 2 38
53 87 63 52 61 22 117 13 28 4 77 88 55 36 32 30 56 93
110 1 51 103 7 18 26 113 86 50 84 20 72 23 83 112 33 99
12 102 101 31 49 90 71 37 73 6 67 60 9 54 40 76 19 43
21 39 104 114 44 48 89 45 118 119 75 105]
理解万岁
最后我们来画出我们能的预测函数
plt.scatter(train_x,train_labels)
x = np.array([min(train_x),max(train_x)])
with torch.no_grad():
y = w.numpy()*x+b.numpy()
plt.plot(x,y,color='red')
plt.colorbar() # 显示颜色条
plt.show()
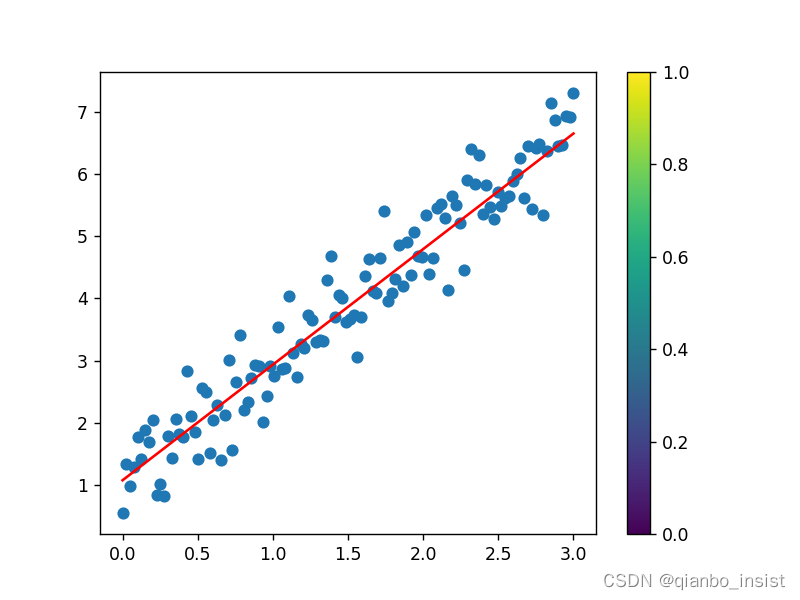
预测函数出来了,我们可以清晰地看到红色的直线。
到gpu执行
最后我们把数据放到gpu执行,执行的时候to就行了
device = 'cuda' if torch.cuda.is_available() else 'cpu'
print('Doing computations on '+device)
w = torch.tensor([100.0],requires_grad=True,dtype=torch.float32,device=device)
b = torch.zeros(size=(output_dim,),requires_grad=True,device=device)
def f(x):
return torch.matmul(x,w) + b
def compute_loss(labels, predictions):
return torch.mean(torch.square(labels - predictions))
def train_on_batch(x, y):
predictions = f(x)
loss = compute_loss(y, predictions)
loss.backward()
w.data.sub_(learning_rate * w.grad)
b.data.sub_(learning_rate * b.grad)
w.grad.zero_()
b.grad.zero_()
return loss
batch_size = 4
for epoch in range(10):
for i in range(0,len(features),batch_size):
### Changes here: move data to required device
loss = train_on_batch(features[i:i+batch_size].view(-1,1).to(device),labels[i:i+batch_size].to(device))
print('Epoch %d: last batch loss = %.4f' % (epoch, float(loss)))
读者可以尝试一下上面的代码,等到下一次 第二篇再讲了