从零开始进行高精度手眼标定 eye in hand(小白向)1 原理推导
- 前言
- 原理推导
- 算法框图
- MATLAB编程计算
- 相关优化工具箱的安装(不安装会报错)
- 数据读取
- 目标函数计算
- 完整代码
- 实验验证
传送门:
1.【从零开始进行高精度手眼标定 eye in hand(小白向)1 原理推导】
2.【从零开始进行高精度手眼标定 eye in hand(小白向)2 Tsai轴角法与四元数法编程实现】
3.【从零开始进行高精度手眼标定 eye in hand(小白向)3 非线性高精度标定法编程实现】
前言
最近由于组内的相关工作需求,需要进行机器人的高精度标定。原始的标定精度在6mm左右,虽然听起来是非常微小的偏差,但是由于研究方向手术机器人对精度要求极高。且在运动过程中,深度信息误差、畸变误差、机械误差、坐标系转换等一系列误差累积环节,将导致误差放大,因此远不能达到要求。
在经过了为其两周的研究和编程探索,最后成功将标定精度提升到0.5mm,达到了任务要求。
使用规划和智能算法对相机进行标定具有比较强的优势在于,不管是非线性规划的方法还是粒子群/遗传等智能方法的计算目标函数可以将旋转矩阵与位移矩阵一起进行计算,这种计算方法也被称之为一步法,对比传统的Tsai手眼标定的两步法可以有效避免旋转矩阵和位移矩阵计算的误差积累。当然缺点是非常不好进行编程实现,且一旦编程出现错误极有可能误差巨大,而且数学要求较高,需要一定的数学基础。
本系列的重点有三个:
- 原理中A,B矩阵的推导和代码计算
- Tsai轴角方法和四元数等二步计算方法的实现
- 基于非线性优化的高精度手眼标定方法的原理与代码实现
原理推导
算法框图

MATLAB编程计算
相关优化工具箱的安装(不安装会报错)
主要需要的相关工具箱进行优化求解:
不知道matlab怎么安装工具箱的同学也可以走传送门:
优秀的同学就可以直接自己往下看
数据读取
%% RobotEffectorPose; %机器人末端位姿导入
img_num = 10;
x = load("E:\研究生学习\手眼标定\IMG_20230516_5\pos.txt");
pos = zeros(4,4,img_num);
% 各个点机械臂位姿变化矩阵
for i=1:1:img_num
pos(:,:,i) = x(((4*(i-1)+1):4*i),:);
end
% 相邻机械臂位姿变化增量
for i=1:1:img_num-1
A_add(:,:,i)= pos(:,:,i)\pos(:,:,i+1);
end
% 矩阵拼接
A = [];
for i=1:1:img_num-1
A(:,:,i) = A_add(:,:,i);
end
B = [];
%% 相机标定数据导入
load('calibrationSession0516_5.mat')
for i=1:1:img_num-1
Rr1 = calibrationSession.CameraParameters.RotationMatrices(:,:,i);
Rr2 = calibrationSession.CameraParameters.RotationMatrices(:,:,i+1);
Tr1 = calibrationSession.CameraParameters.TranslationVectors(i,:);
Tr2 = calibrationSession.CameraParameters.TranslationVectors(i+1,:);
B_add = [Rr1' (Tr1/1000)';0,0,0,1]/[Rr2' (Tr2/1000)';0,0,0,1];
B(:,:,i) = B_add;
end
中需要注意的两点是数据的输入格式
其中矩阵A的输入为:
x = load("E:\研究生学习\手眼标定\IMG_20230516_3\pos.txt");
pos.tx文件中储存的是机械臂各个位姿点,由机器人基座标系到末端坐标系的变换矩阵
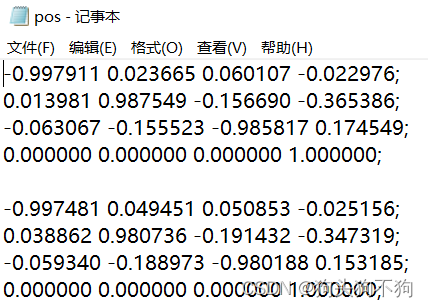
矩阵B的输入为:
load('calibrationSession0516_3.mat')
其中calibrationSession0516_3.mat是通过相机标定工具箱保存在代码同一文件夹下的标定参数
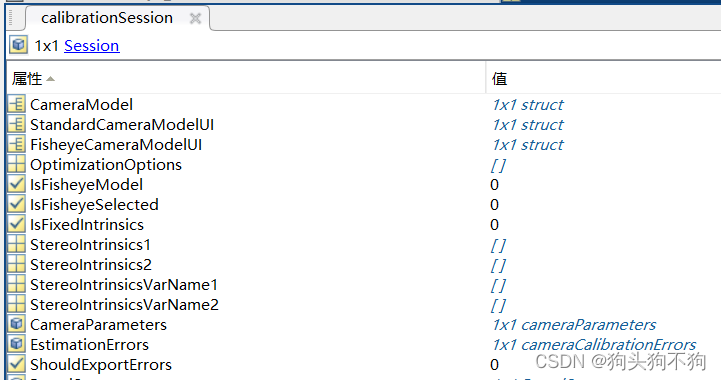
目标函数计算
X=[q0^2+q1^2-q2^2-q3^2 2*(q1*q2-q0*q3) 2*(q1*q3-q0*q2) t1
2*(q1*q2-q0*q3) q0^2-q1^2+q2^2-q3^2 2*(q2*q3-q0*q1) t2
2*(q1*q3-q0*q2) 2*(q2*q3-q0*q1) q0^2-q1^2-q2^2-q3^2 t3
0 0 0 1];
%% 根据几何误差创建关于X的目标函数
fx_sum = 0;
for i = 1:img_num-1
fx = A(:,:,i)*X-X*B(:,:,i);
fx_transpose = transpose(fx); % 计算矩阵的转置
fx_norm_2 = trace(fx * fx_transpose); % 计算矩阵的二范数平方
% fx_norm_2 = sqrt(sigma_max); % 计算二范数(最大奇异值的平方根)
% fx_norm_2 = norm(fx, 'fro')^2; % 计算矩阵A的二范数
fx_sum = fx_sum + fx_norm_2;
end
Fx = fx_sum /(img_num-1);
完整代码
代码目前由于还涉及项目问题不准备完全公开,可能晚一些时间等项目结束会更新博客内容。感谢理解。
我会上传部分关键代码在资源,有能力的同学可以尝试根据博客内容补齐:
基于非线性优化的高精度手眼标定关键部分代码
完整代码和答疑真正需要的同学可以私信联系我,请私信表明来意和代码用途
实验验证
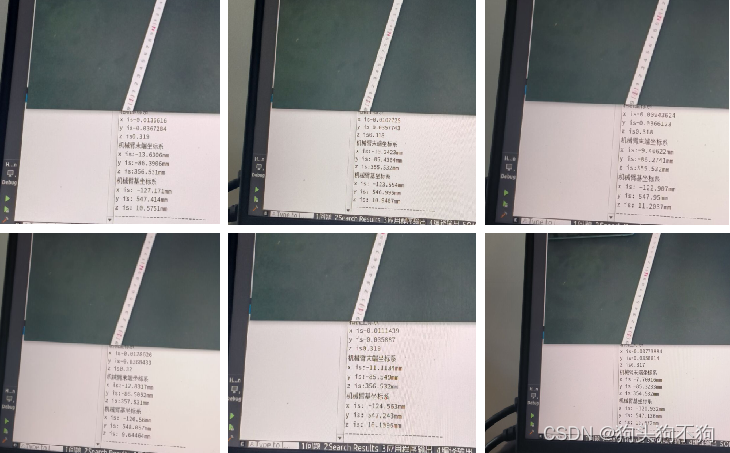
经过实验测量以y轴精度进行验证,整机验证进行六次采集,平均精度误差为0.361mm
在本次中参考论文:
[1]LI, W., LYU, N., DONG, M., & LOU, X. (2017). Robot hand-eye calibration by convex relaxation global optimization. Journal of Computer Applications, 37(5), 1451.
[2]李巍, 吕乃光, 董明利, & 娄小平. (2017). 凸松弛全局优化机器人手眼标定. 计算机应用, 37(5), 1451-1455.