目录
1.题目:
题目描述
输入格式
输出格式
2.思路
1.ans数组的维护
2.L and R 的维护
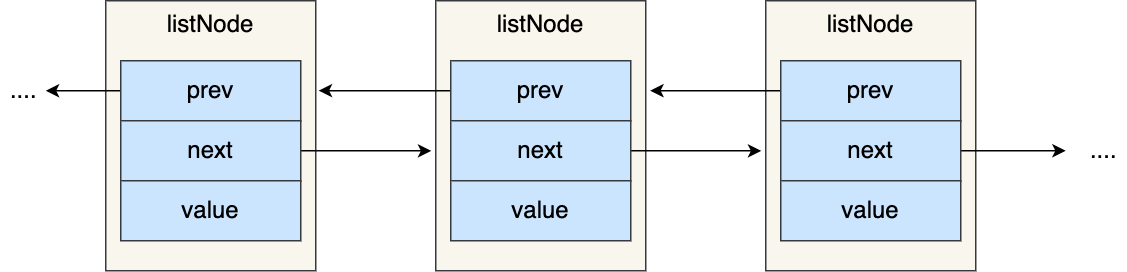
3.ne数组与pr数组的维护
4.len数组:
3.代码:
1.有注释版:
2.copy版:
1.题目:
题目描述
给定一个长度为N的字符序列 ,初始时序列中全部都是字符L。
有 q次修改,每次给定一个 x,若为L,则将
修改成R,否则将
修改成L。
对于一个只含字符 L,R的字符串S,若其中不存在连续的L和R,则称 S满足要求。
每次修改后,请输出当前序列
中最长的满足要求的连续子串的长度。
输入格式
第一行有两个整数,分别表示序列的长度 n 和修改操作的次数 q。
接下来 q 行,每行一个整数,表示本次修改的位置 x。
输出格式
对于每次修改操作,输出一行一个整数表示修改 a 中最长的满足要求的子串的长度。
一句话解释(不知道大家了解不) :最长01交替字串
2.思路
我们循序渐进,慢慢分析:(码力重点呀!!!)
首先:单点修改,动态维护最长,很明显是线段树
那么:首先,应该有一个数组
来记录最长的字串。
1.ans数组的维护
继续分析:
区区线段树,必有的操作是建一棵树(此处以区间和为基准)。void build(int l,int r,int k) { if(l==r){cin>>c[k];return;} int mid=(l+r)>>1; build(l,mid,lk); build(mid+1,r,lk|1); c[k]=c[lk]+c[lk|1]; }//oh,lk与rk是define,后文有注意一下:
最后一排
c[k]=c[lk]+c[lk|1];是一个合并的过程。
但题目描述中提到:能否合并,must 左区间的右端点 != 右区间的左端点
所以拿两个数组:
表示
左端点是什么 ,
表示
右端点是什么。
那么,就可以推如何合并了。
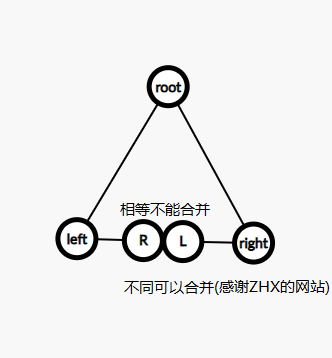
如果ans[root]的左区间的右端点=ans[root]的右区间的左端点,那么不满足要求,代码就是
ans[root]=max(ans[root<<1],ans[root<<1|1]) /* 注意,我这里用的是位运算(个人喜好) root<<1 就是root*2 root<<1|1 就是root*2+1(因为<<1保证了root二进制的末尾为0,所以或1后就得root+1) */如果ans[root]的右区间的左端点!=ans[root]的左区间的右端点,那么就可以合并。
蒙了吧?我也蒙了来人!本蒟蒻的树呢?
(图片来源:Graph Editor (csacademy.com))
那么相等怎么合并呢???(更晕的来了)
就是上图中以R为右端点的最长01字串+以L为左端点的最长01字串的和,在
与
的最大值作比较,取最大值。
综合就是:
#define lk k<<1 a[k]=max(a[lk],r[lk]!=l[rk]?max(a[rk],ne[lk]+pr[rk]):a[rk]);//ne数组是后缀,pr数组是前缀。所以像消消乐一样,只有下面几个问题等我们维护:
- R 数组的维护
- L 数组的维护
- ne 数组的维护
- pr 数组的维护
所以慢慢看······
2.L and R 的维护
这个简单呀!!!
你 ans[root*2]的左端点 就一定是 ans[root]的左端点
ans[root<<1|1]的右端点 就一定是ans[root]的右段点
(啥?why??)
给张图:
可以理解了吧!
3.ne数组与pr数组的维护
直接来吧······
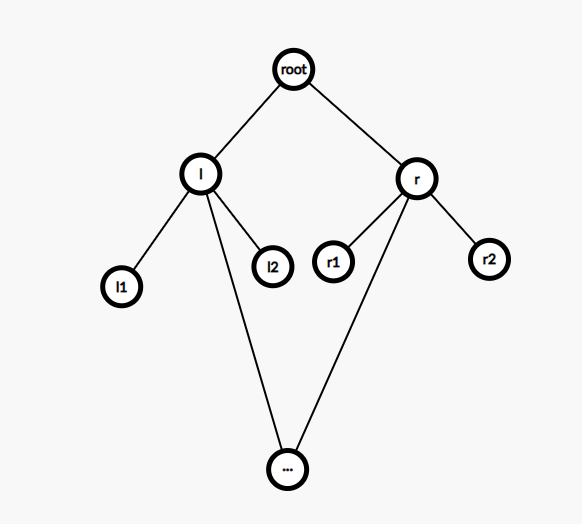
如果ne[rook*2]数组没有覆盖van左区间
那很明显,根节点的ne就是左区间的ne,
同样,pr[rook*2+1]数组没有覆盖van右区间
根节点的pr就是右区间的pr。
给张图:
如果到已经l2已经不能继续了,那么从l1开始的ne 就只能到l2
R也一样。
但如何判断是否能覆盖呢?
所以还要引入len数组。
4.len数组:
很简单,建树时直接赋值即可。
3.代码:
1.有注释版:
#include<bits/stdc++.h>
using namespace std;
#define lk k<<1
#define rk k<<1|1
const int N=2e5;
int n,q,x,len[N*4+10],a[N*4+10],l[N*4+10],r[N*4+10],pr[N*4+10],ne[N*4+10];
inline int read()//快读
{
int x=0,w=0;char c=0;
while(!isdigit(c)) {w|=c=='-';c=getchar();}
while(isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
return w?-x:x;
}
void change(int k)
{
a[k]=max(a[lk],r[lk]!=l[rk]?max(a[rk],ne[lk]+pr[rk]):a[rk]);//维护总长度
l[k]=l[lk];//维护L
r[k]=r[rk];//维护R
if(pr[lk]==len[lk]&&r[lk]!=l[rk]) pr[k]=pr[lk]+pr[rk];//维护pr
else pr[k]=pr[lk];//维护pr
if(ne[rk]==len[rk]&&r[lk]!=l[rk]) ne[k]=ne[lk]+ne[rk];//维护ne
else ne[k]=ne[rk];//维护ne
}
void build(int ll,int rr,int k)//建树
{
len[k]=rr-ll+1;//维护len
if(ll==rr) {a[k]=pr[k]=ne[k]=1;return;}
int mid=(ll+rr)>>1;
build(ll,mid,lk),build(mid+1,rr,rk);
change(k);
}
void modify(int x,int ll,int rr,int k)//修改
{
if(ll==rr)
{
a[k]=pr[k]=ne[k]=1;
l[k]=(l[k]==0?1:0),r[k]=(r[k]==0?1:0);//维护l ,r
return ;
}
int mid=(ll+rr)>>1;
if(x<=mid) modify(x,ll,mid,lk);
else modify(x,mid+1,rr,rk);
change(k);
}
int main()
{
n=read(),q=read();
build(1,n,1);
while(q--)
{
x=read();
modify(x,1,n,1);
printf("%d\n",a[1]);
}
return 0;
}2.copy版:
#include<bits/stdc++.h>
using namespace std;
#define lk k<<1
#define rk k<<1|1
const int N=2e5;
int n,q,x,len[N*4+10],a[N*4+10],l[N*4+10],r[N*4+10],pr[N*4+10],ne[N*4+10];
inline int read()
{
int x=0,w=0;char c=0;
while(!isdigit(c)) {w|=c=='-';c=getchar();}
while(isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
return w?-x:x;
}
void change(int k)
{
a[k]=max(a[lk],r[lk]!=l[rk]?max(a[rk],ne[lk]+pr[rk]):a[rk]);
l[k]=l[lk];
r[k]=r[rk];
if(pr[lk]==len[lk]&&r[lk]!=l[rk]) pr[k]=pr[lk]+pr[rk];
else pr[k]=pr[lk];
if(ne[rk]==len[rk]&&r[lk]!=l[rk]) ne[k]=ne[lk]+ne[rk];
else ne[k]=ne[rk];
}
void build(int ll,int rr,int k)
{
len[k]=rr-ll+1;
if(ll==rr) {a[k]=pr[k]=ne[k]=1;return;}
int mid=(ll+rr)>>1;
build(ll,mid,lk),build(mid+1,rr,rk);
change(k);
}
void modify(int x,int ll,int rr,int k)
{
if(ll==rr)
{
a[k]=pr[k]=ne[k]=1;
l[k]=(l[k]==0?1:0),r[k]=(r[k]==0?1:0);
return ;
}
int mid=(ll+rr)>>1;
if(x<=mid) modify(x,ll,mid,lk);
else modify(x,mid+1,rr,rk);
change(k);
}
int main()
{
n=read(),q=read();
build(1,n,1);
while(q--)
{
x=read();
modify(x,1,n,1);
printf("%d\n",a[1]);
}
return 0;
}(L('ω')┘点赞,关注,下篇博客再见 └('ω')」)