文章目录
- 3.数字逻辑
- 3.1 MOS管
- 3.1.1 p型MOS晶体管
- 3.1.2 n型MOS晶体管
- 3.2 逻辑门
- 3.2.1 非门——反相器
- 3.2.2 或非门、或门
- 或非门
- 或门
- 3.2.3 与非门、与门
- 3.2.4 逻辑门符号表示
- 逻辑门的数电表达式
- 摩根定律
- 3.3 逻辑结构
- 3.3.1 组合逻辑
- 译码器
- 多路复用器
- 全加器
- 可编程逻辑阵列
- 3.3.2 存储单元
- R-S锁存器
- 门控D锁存器
- 寄存器
- 内存
- 3.4 时序电路
- 3.4.1 有限状态机
- 状态图
- 时钟
- 3.4.2 有限状态机的实现
- 3.5 习题
3.数字逻辑
- MOS晶体管工作原理
- 如何基于MOS晶体管实现逻辑门
- 如何通过逻辑门互连构建计算机的组成单元
3.1 MOS管
MOS管(metal-oxide semicconductor) 金属氧化物半导体
- 通常情况下假设MOS晶体管工作稳定,不会出现问题。
- 其底层属于电气特性,属于电子学
使电路工作,需要满足两个条件:电源和闭合回路
MOS管相当于电路中开关的作用
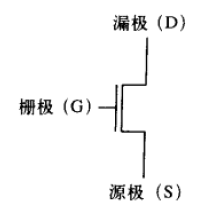
- 栅极:使能端
- 源极、漏极:接入电路的两端
在栅极接通时,源极与漏极之间会形成一条通路——导通、闭路状态
源极和漏极之间断开,则处于——断开、开路状态
3.1.1 p型MOS晶体管
低连通
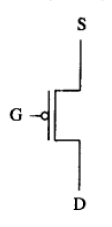
在栅极接入2.9V电压,源极和漏极断开
在栅极接入小于2.9V的电压,源极和漏极导通
3.1.2 n型MOS晶体管
高连通
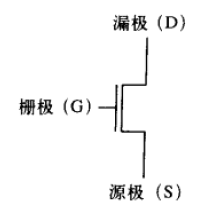
在栅极接入2.9V电压,源极和漏极导通
在栅极接入小于2.9V的电压,源极和漏极断开
同时包含p-MOS管和n-MOS管的的电路称为CMOS电路——(互不金属氧化物半导体,Complementary Metal-Oxide Semiconductor)
3.2 逻辑门
将实现逻辑函数的COMS电路称为逻辑门电路
3.2.1 非门——反相器
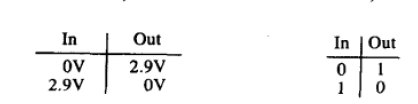
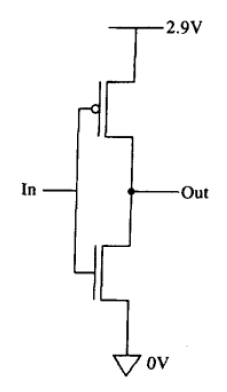
- 一个p-型MOS管
- 一个n-型MOS管
3.2.2 或非门、或门
或非门
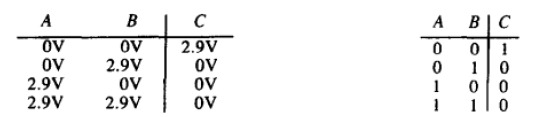
- 两个p-型MOS管
- 两个n-型MOS管
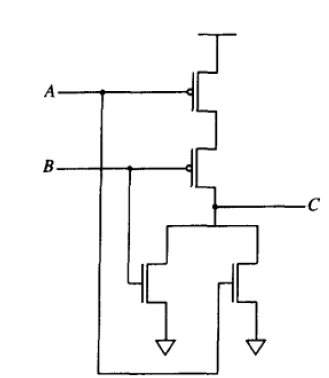
或门
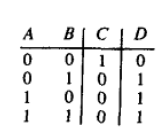
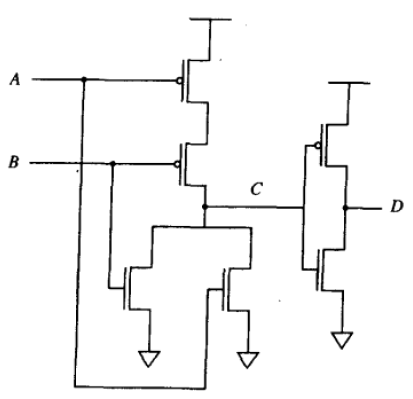
- 三个p-型MOS管
- 三个n-型MOS管
3.2.3 与非门、与门
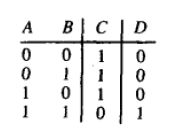
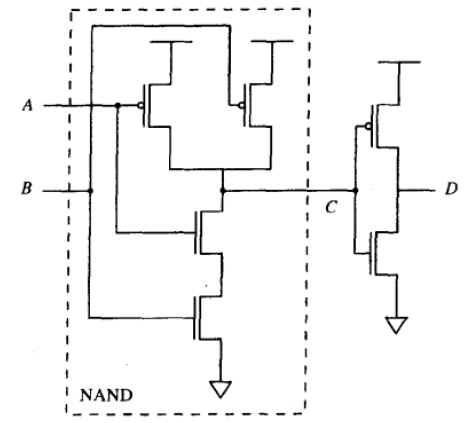
- 三个p-型MOS管
- 三个n-型MOS管
3.2.4 逻辑门符号表示
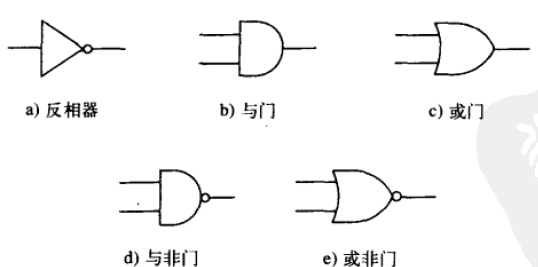
逻辑门的数电表达式
x ‾ \overline{x} x 表示 x x x 的非
a ⋅ b a\cdot b a⋅b 表示 a a a 和 b b b 相与
a + b a+b a+b 表示 a a a 和 b b b 相或
摩根定律
a ⋅ b ‾ = a ‾ + b ‾ \overline{a\cdot b}=\overline{a}+\overline{b} a⋅b=a+b
a + b ‾ = a ‾ ⋅ b ‾ \overline{a+b}=\overline{a}\cdot \overline{b} a+b=a⋅b
3.3 逻辑结构
逻辑结构分为两大类:不可存储信息——组合逻辑;可存储信息——存储单元
3.3.1 组合逻辑
组合逻辑(“决策单元”)的输出状态完全取决于当前逻辑结构的输入
- 译码器
- 多路复用器
- 全加器
译码器
用于解释一个二进制数
在特定的输入模式下,相应的输出线被置位
- n个输入, 2 n 2^n 2n 个输出
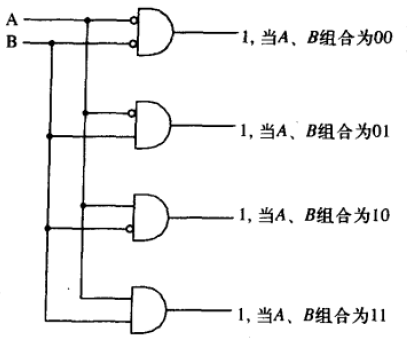
多路复用器
从多个输入中选择一个
- 2 n 2^n 2n 个输入,一个输出,n个选择线
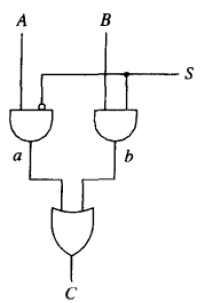
全加器
1bit全加器
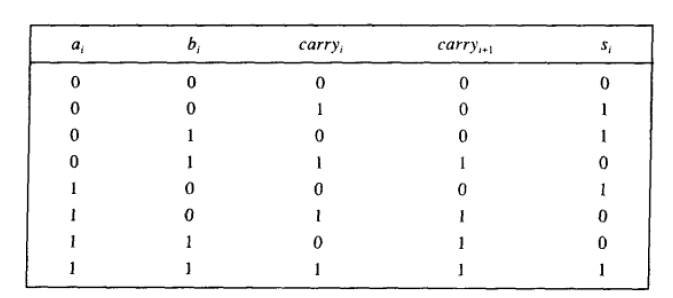
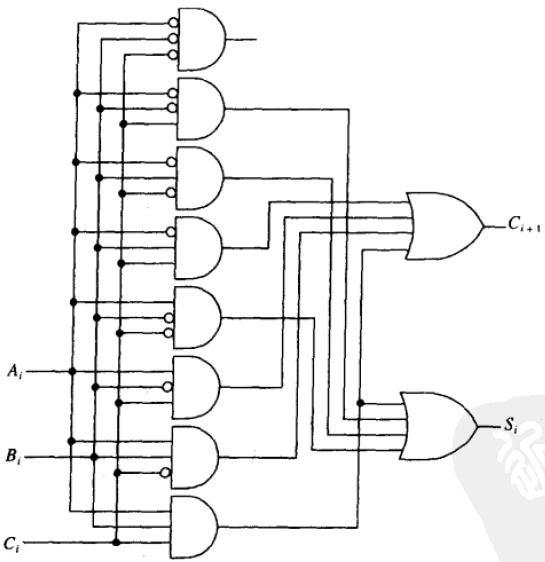
逻辑表达式
s i = a i ⊕ b i ⊕ c a r r y i s_i=a_i\oplus b_i\oplus carry_i si=ai⊕bi⊕carryi
- 奇数个1置1
- 偶数个1或者3个0,置0
c a r r y i + 1 = c a r r y i ( a i ⊕ b i ) + a i b i carry_{i+1}=carry_i(a_i\oplus b_i)+a_ib_i carryi+1=carryi(ai⊕bi)+aibi
- 三个输入中多于2个1,则有进位
4bit全加器
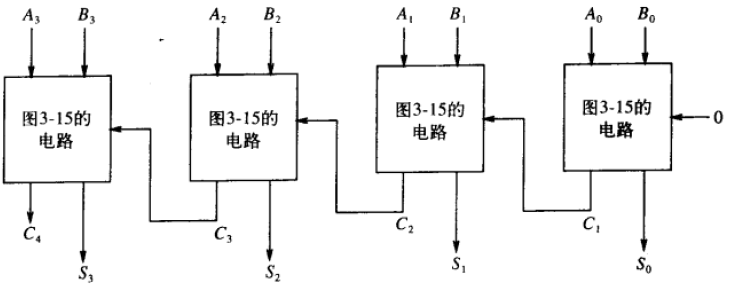
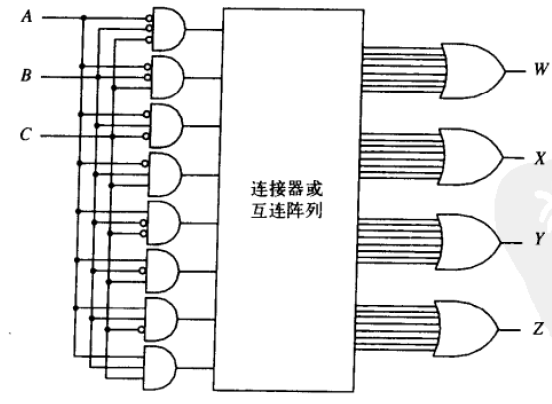
可编程逻辑阵列
逻辑门的组合可以实现不同的输出值组合
可编程阵列(Programmable Logic Array,PLA)
通过“编程”多个与门(不同输入组合)与多个或门(不同输出组合)之间的连接关系,可以实现任何逻辑函数
逻辑完备性
PLA只要有与或非三种逻辑门,就可以实现任何逻辑函数。
- 因为与或非是逻辑完备的
3.3.2 存储单元
可以存储电路的历史信息,但不具备数据处理能力
R-S锁存器
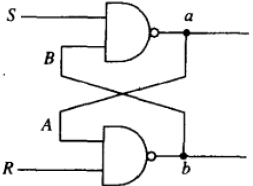
- R=1,S=1,锁存——静态,输出不变
- R=1不变,S置0,输出置1
- S=1不变,R置1,输出置0
- R=0,S=0,锁存器状态不确定
静态
- a = 1 ⇒ b = B = 0 ⇒ a = 1 a=1\Rightarrow b=B=0\Rightarrow a=1 a=1⇒b=B=0⇒a=1
- a = 0 ⇒ b = B = 1 ⇒ a = 0 a=0\Rightarrow b=B=1\Rightarrow a=0 a=0⇒b=B=1⇒a=0
S=0输出置1
清除S, S = 0 ⇒ a = 1 ⇒ b = 0 ⇒ a = 1 S=0\Rightarrow a=1\Rightarrow b=0\Rightarrow a=1 S=0⇒a=1⇒b=0⇒a=1
此时,S变为1,则锁存器处于静态
- a = 1 ⇒ b = 0 ⇒ a = 1 a=1\Rightarrow b=0\Rightarrow a=1 a=1⇒b=0⇒a=1
R=0输出置0
清除R, R = 0 ⇒ b = 1 ⇒ a = 0 R=0\Rightarrow b=1\Rightarrow a=0 R=0⇒b=1⇒a=0
若R变为1,则锁存器进入静态
- a = 0 ⇒ b = 1 ⇒ a = 0 a=0\Rightarrow b=1\Rightarrow a=0 a=0⇒b=1⇒a=0
门控D锁存器
R-S锁存器+控制电路
只有(写入)控制信号 WE=1 有效时,才使锁存器的值等于输入值D
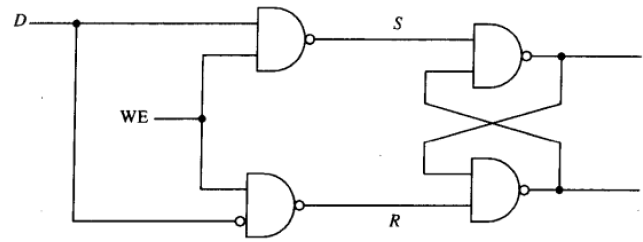
WE无效时,RS都等于1,R-S锁存器处于静态
WE瞬间置位时,两个与非门至少有一个为0
- D=1,S=0,输出=D=1
- D=0,R=0,输出=D=0
寄存器
将多个bit组合成一个独立单元
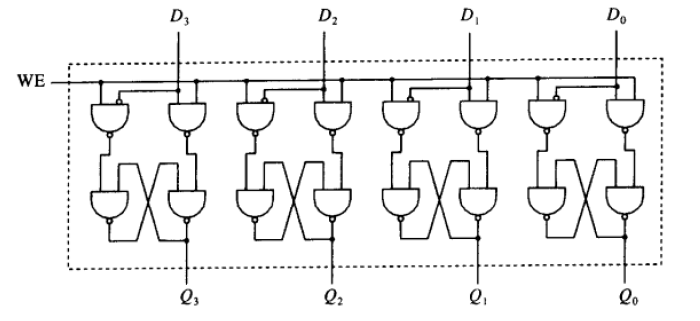
内存
每个 位置 可以被单独识别并独立存放的一个数据
位置标识符称为 地址
存储在位置中的bit数称为 寻址能力
寻址空间 :可独立识别的位置总数
寻址能力:每个内存位置包含的bit 数=存储字长
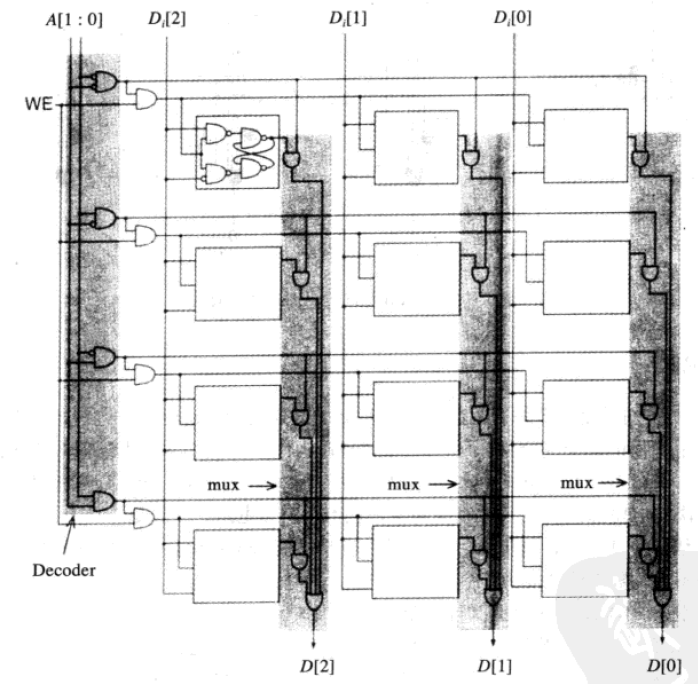
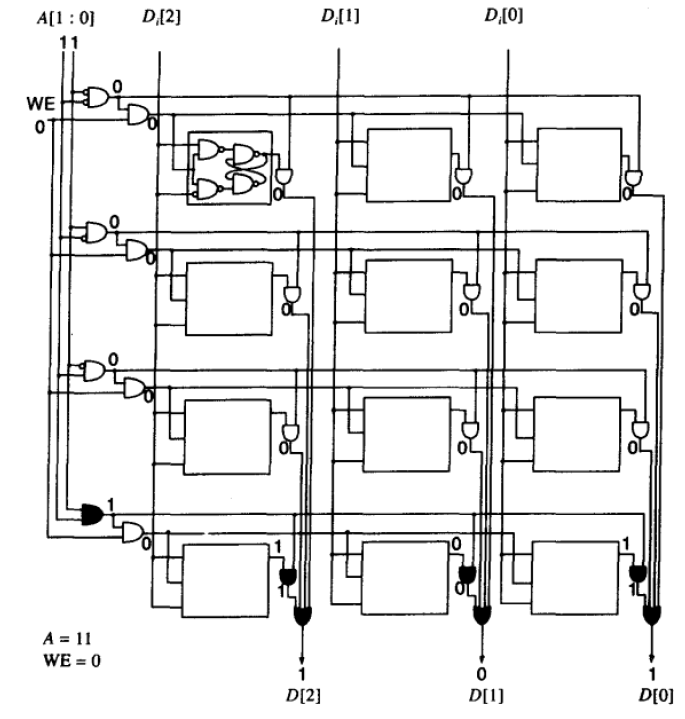
字线 :通过译码器,对应的输出线置1,同字的bit都可被选中
- 每个bit与所在字线相与,与其他字线上的同bit位置相或(当然,由于只有一个字被选中,即一个字线为1,所以输出端的值为所选字的值)
3.4 时序电路
既能处理数据又能存储数据的逻辑电路单元
- 输出与当前输入、之前电路状态相关
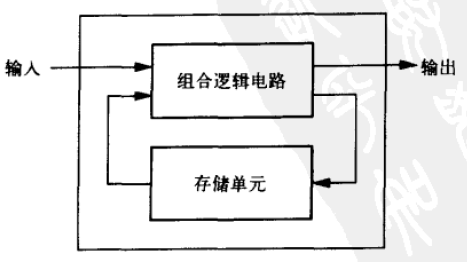
- 存储单元:跟踪电路以前的状态
- 输出:由电路当前输入信号和存储单元信息共同决定
- 状态:系统在特定时刻和特定条件下的快照
3.4.1 有限状态机
组成
- 状态(有限数目)
- 用状态集合表示可能处于的所有状态
- 外部输入(有限数目)
- 对外输出(有限数目)
- 任意状态间迁移(显式注明)
- 从一个状态到另一个状态需要的条件
- 对外输出操作(显式标注)
状态图
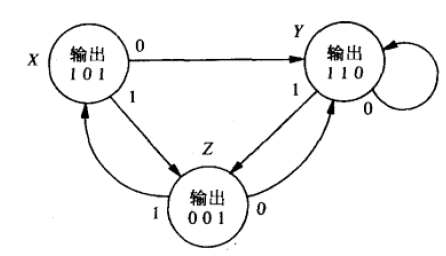
状态结节点:代表系统的一个状态
- 当前状态
- 下一状态
节点间连接线:代表一个状态到另一个状态的转换
- 状态间转移线代表了在当前状态下的所有可能操作(输入)
- 最终的转移取决于外部输入
系统输出既可以由当前状态唯一决定,也可以由当前状态和当前输入共同决定
如:时序锁密码为 R12-L22-R3
- 将输入值与操作历史结合,最终决定是否能将所打开。与旋转过程有关
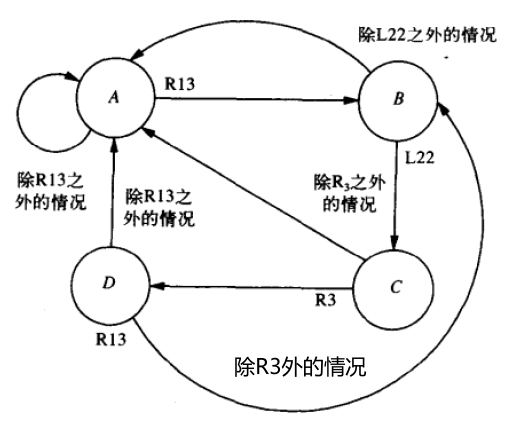
时钟
状态转移的触发机制——状态转移是通过时钟电路来触发的。
- 时钟:01交替变换的信号
有限状态机的状态转移发生在时钟周期的起始时刻
3.4.2 有限状态机的实现
-
外部输入
-
输出
-
存储单元
-
时钟电路
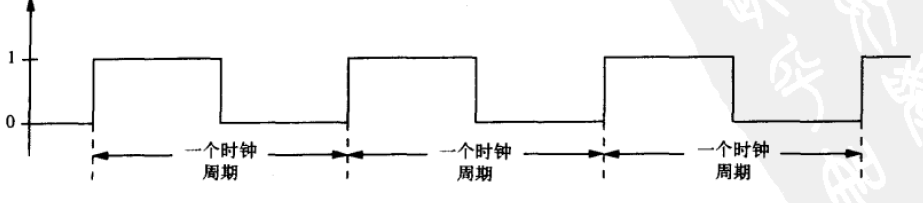
如:交通警示牌
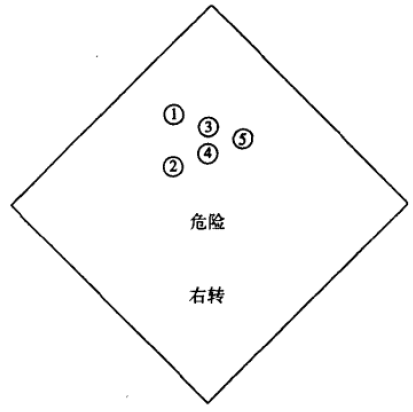
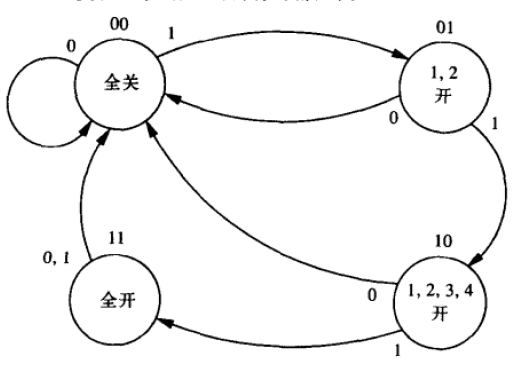
- 外部输入:控制灯亮灭的开关
- 输出:控制1-2号灯亮的操作信号;控制3-4号灯亮的操作信号;控制5号灯亮的操作信号
- 存储单元:记录控制器的当前状态。反映系统之前的状态
- 时钟电路:周期的控制系统的状态转移
组合逻辑
- 外部输出:交通灯的操作信号
- 内部输出:存储单元的状态信息
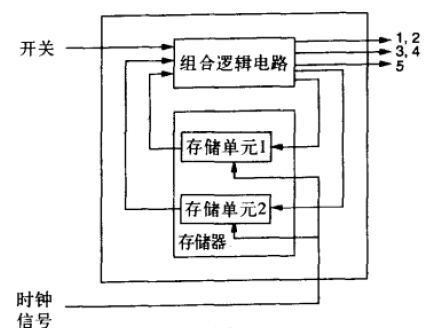
组合逻辑电路:
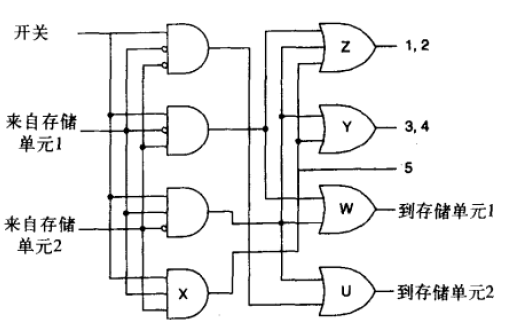
5号灯亮的唯一情况是开关闭合且当前状态为11
3,4号灯亮的情况是开关闭合且状态为10与11
1,2号灯亮的情况为开关闭合且当前状态为01,10与11
存储单元
需要用到主从锁存器
-
由于当前时钟周期内,存储单元的输出是组合逻辑的输入——当前状态
同时组合逻辑的输出又是存储单元的输入,该输入应等到下一时钟周期再写入存储单元
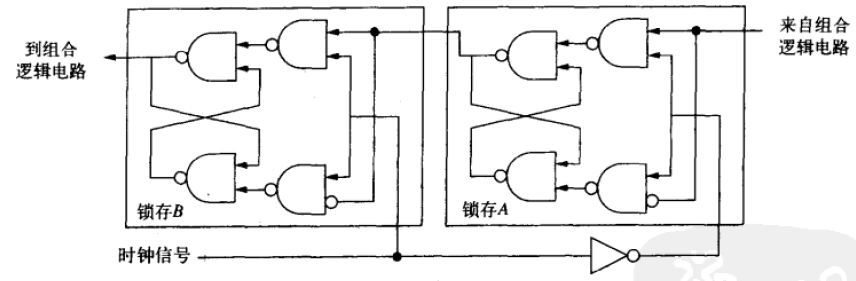
相当于两段式R-S锁存器
当前状态由锁存B输出,下一状态存入锁存A。
- 时钟前半周期,锁存A内容不变,即当前状态不变
- 时钟后半周期,锁存B内容不变,锁存A内容变为下一状态
存储单元1置1的情况是下一状态为10或11,则当前状态为01或10
存储单元2置1的情况是下一状态为01或11,则当前状态为00或10
3.5 习题
3.1
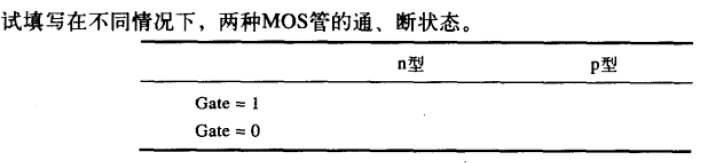
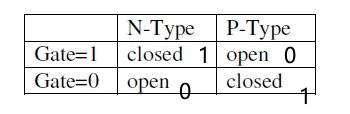
3.2非门
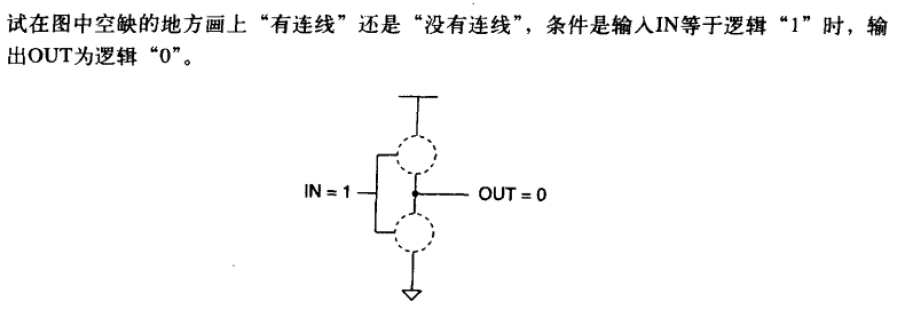
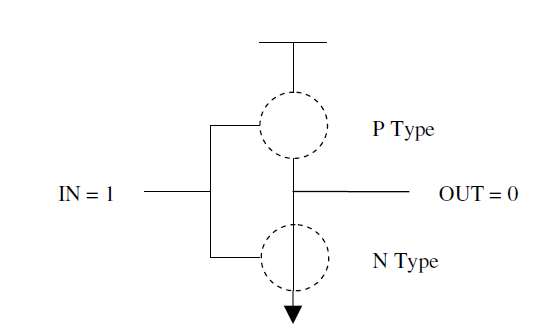
3.3

2输入电路有4种输入组合,相应的每种输出有两种取值,所以理论上有 2 4 = 16 2^4=16 24=16 种两输入逻辑
3.4
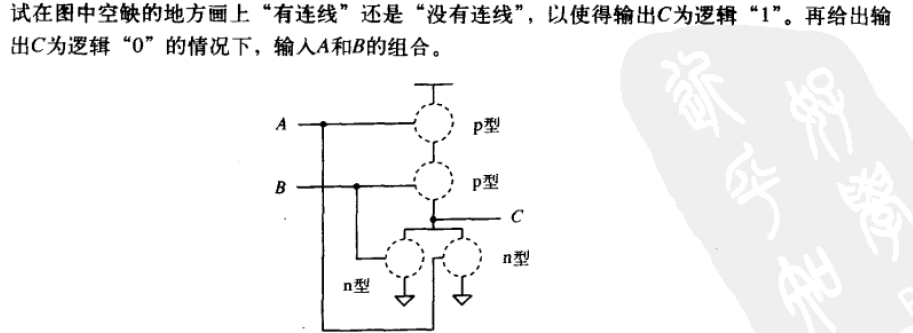
或非门
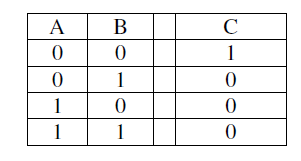
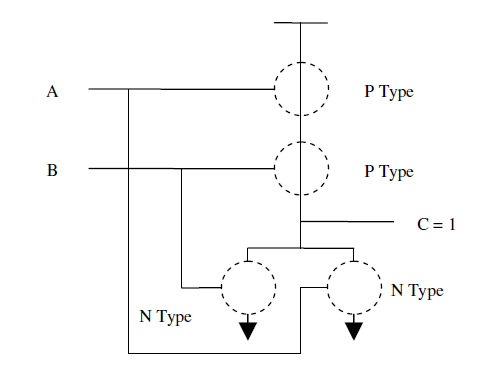
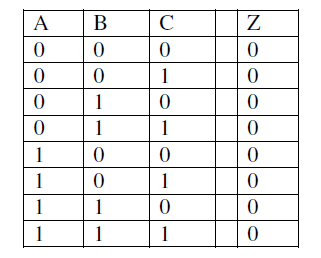
3.5 枚举
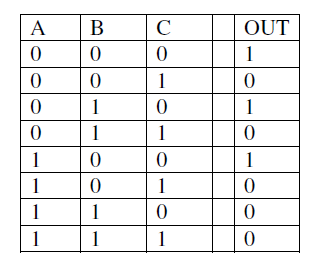
3.6
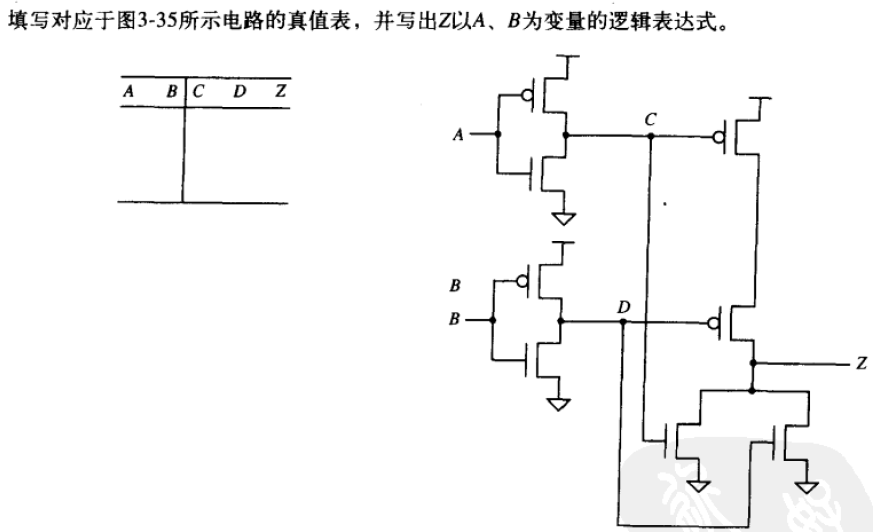
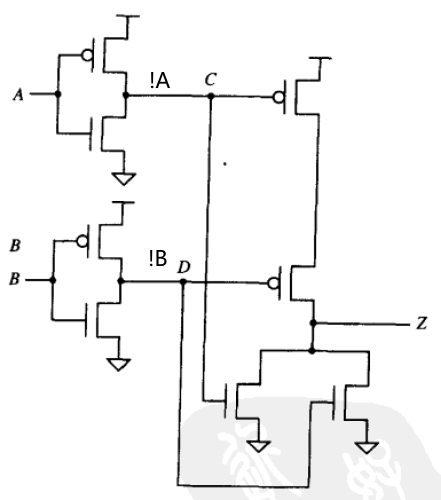
可得逻辑表达式 Z = A ‾ + B ‾ ‾ = A ⋅ B Z=\overline{\overline{A}+\overline{B}}=A\cdot B Z=A+B=A⋅B
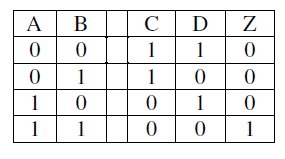
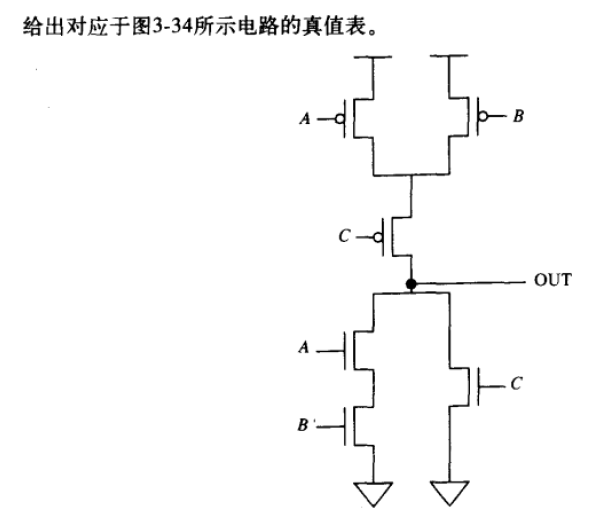
3.7
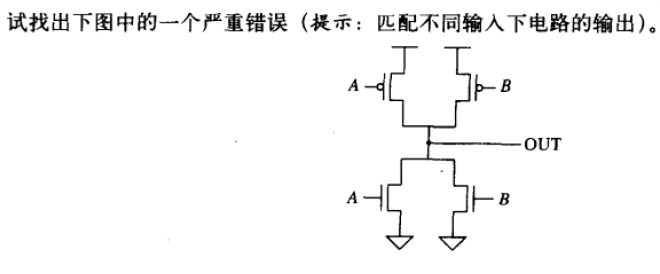
| A | B | OUT |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 冲突 |
| 1 | 0 | 冲突 |
| 1 | 1 | 0 |
在 A ⊕ B = 1 A\oplus B=1 A⊕B=1 的情况下,在源极和漏极之间会形成短路
3.8
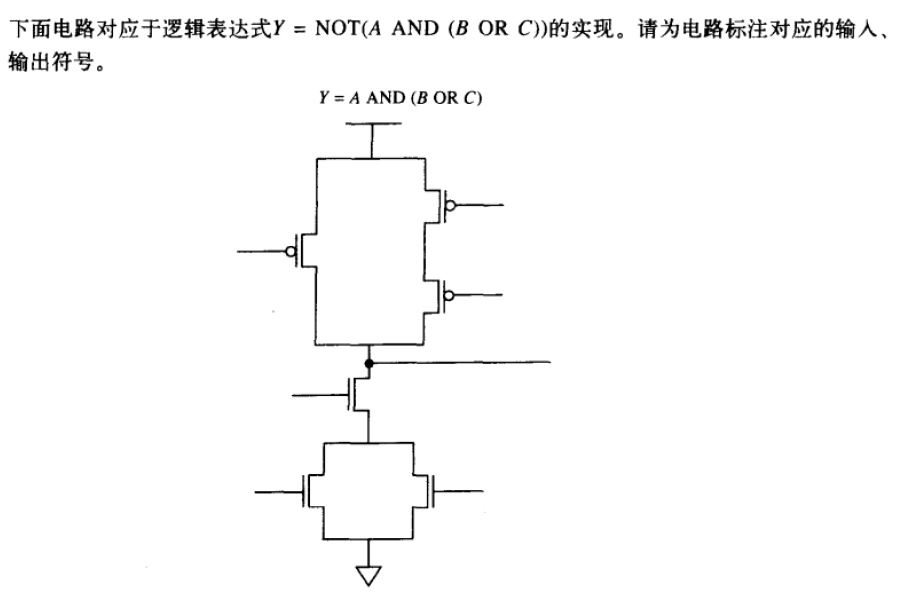
先简化表达式
A ( B + C ) ‾ = A ‾ + B ‾ C ‾ \overline{A(B+C)}=\overline{A}+\overline{B}\overline{C} A(B+C)=A+BC
A为0的情况,则Y一定为1,
A为1,且BC=1时,Y为0
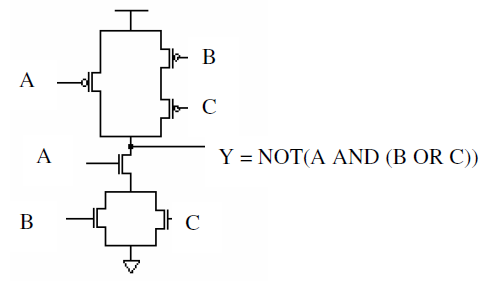
3.9 3.10 都是先化简表达式

3.9为与门,3.10为或非门
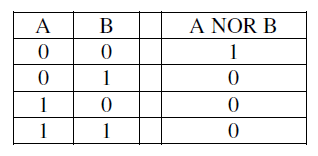
3.11

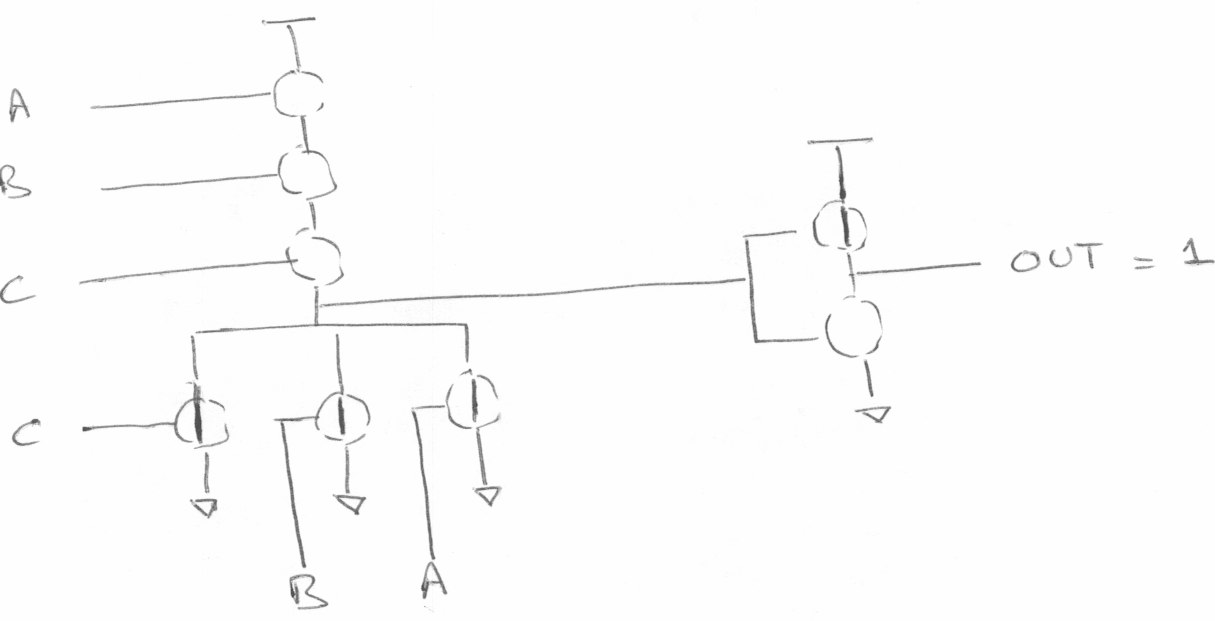
三输入与门,只有 A = B = C = 1 A=B=C=1 A=B=C=1 时,输出为1,其余都为0
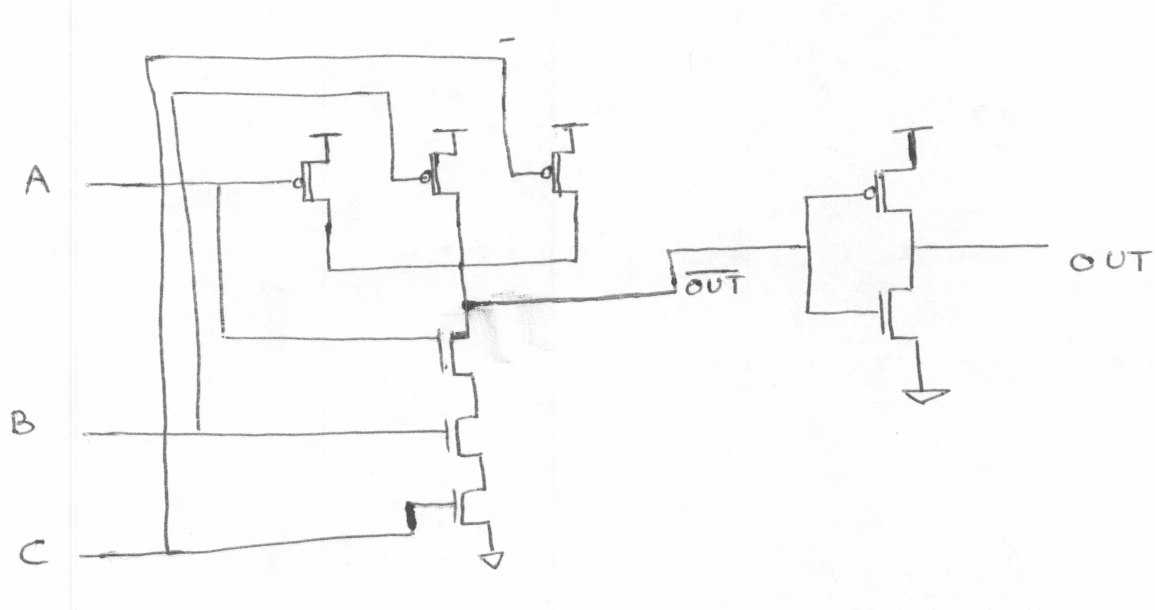
三输入或门
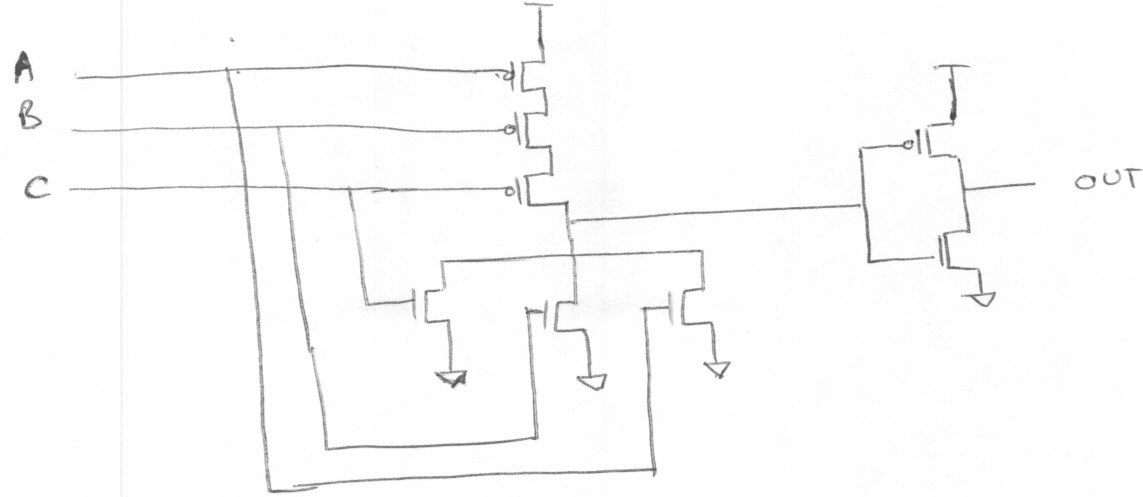
与门标注MOS管的通断
A = 1, B = 0, C = 0.
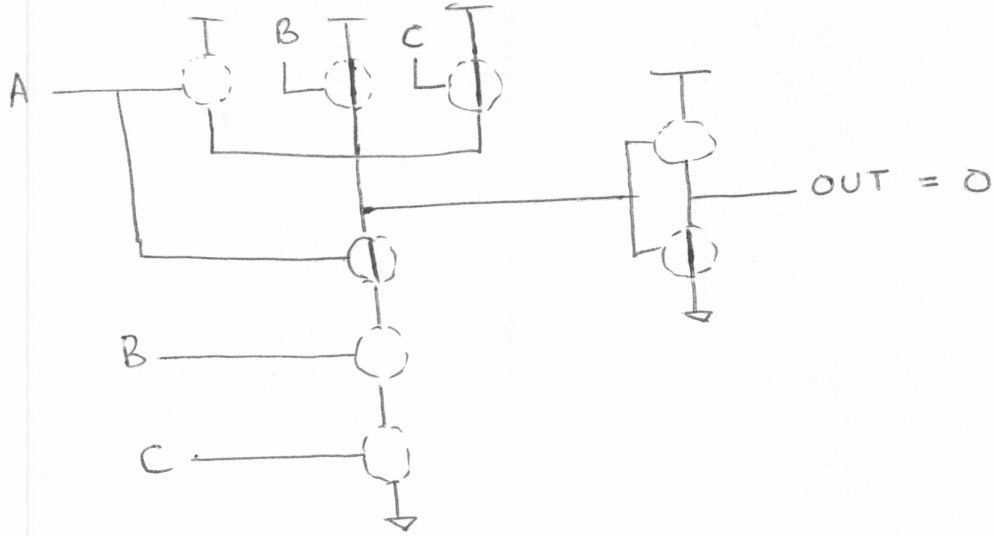
A = 0, B = 0, C = 0
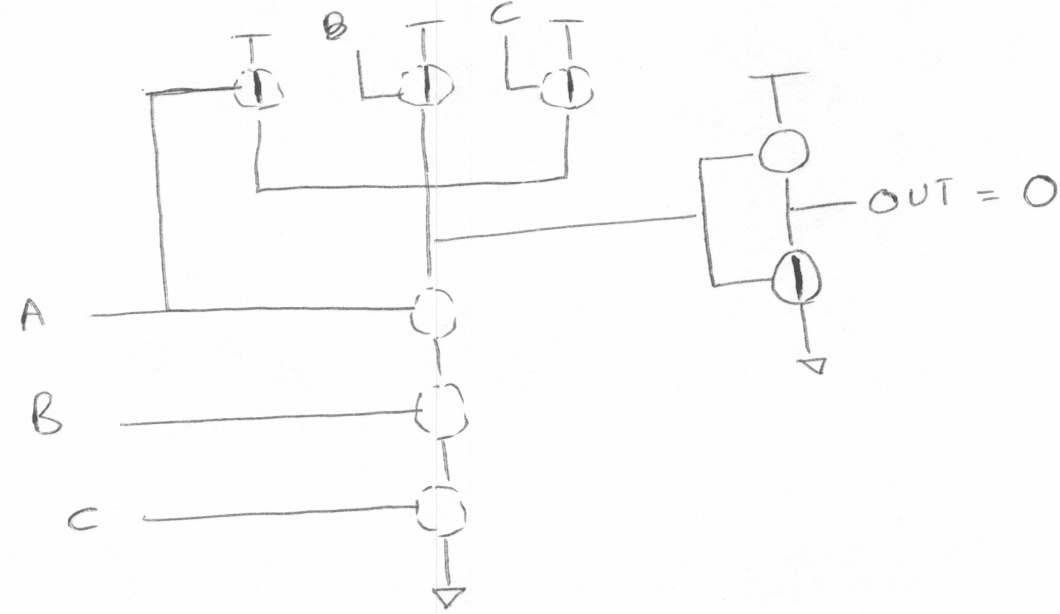
A = 1, B = 1, C = 1
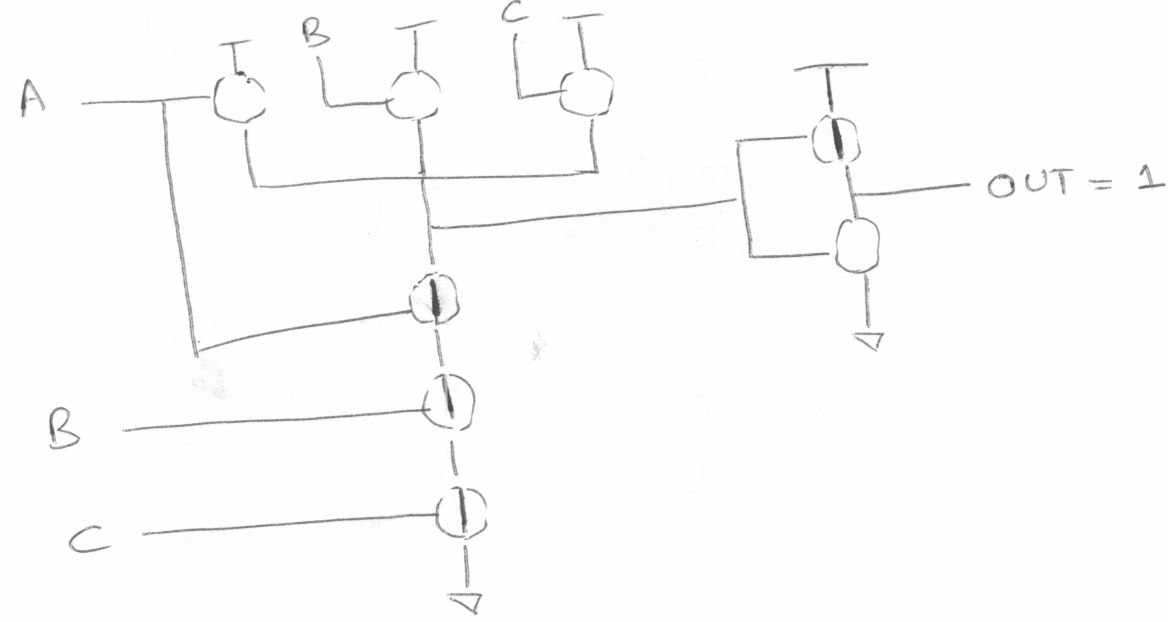
或门标注MOS管的通断
A = 1, B = 0, C = 0
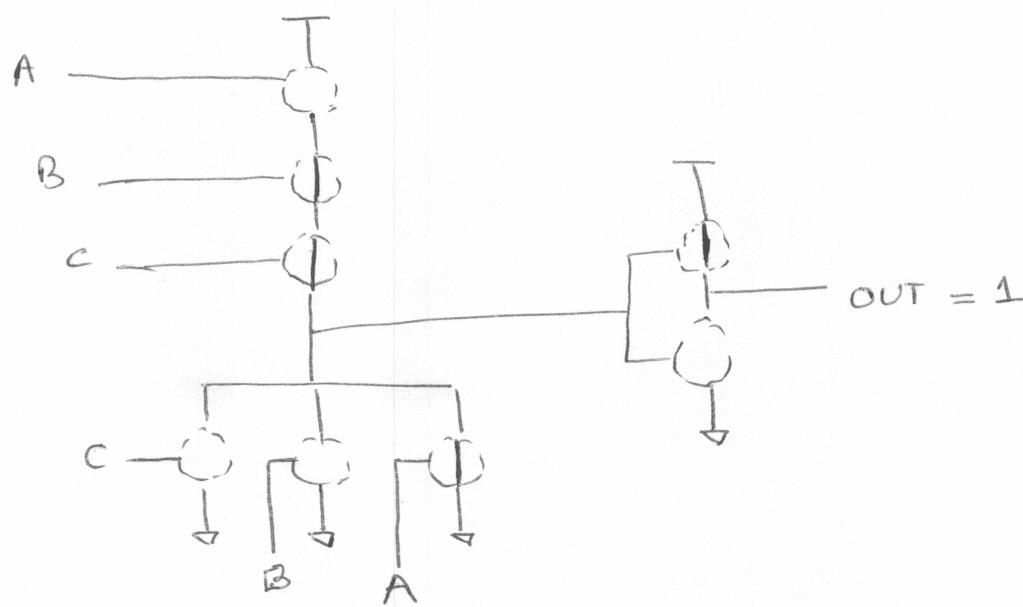
A = 0, B = 0, C = 0
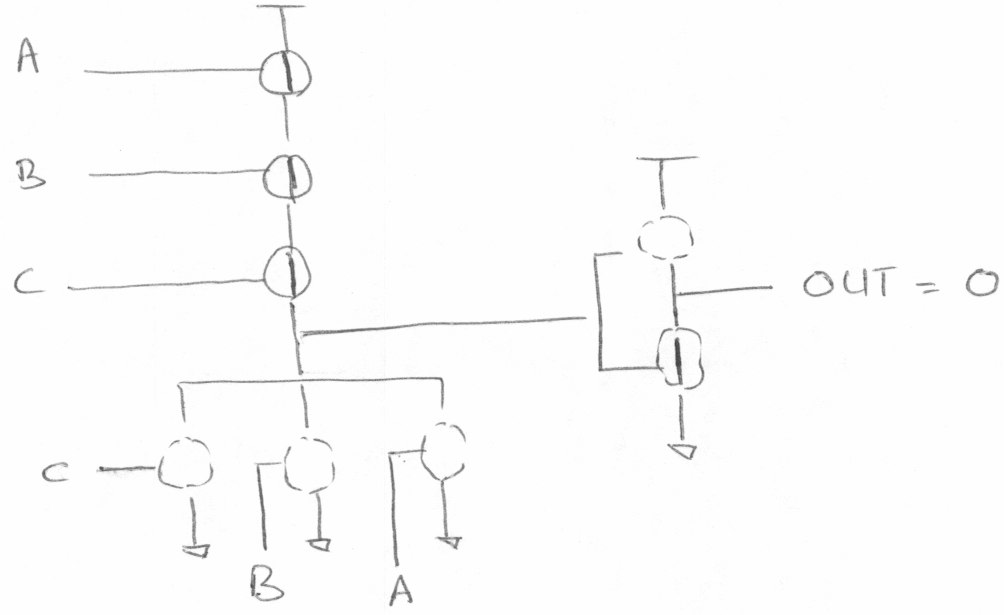
A = 1, B = 1, C = 1
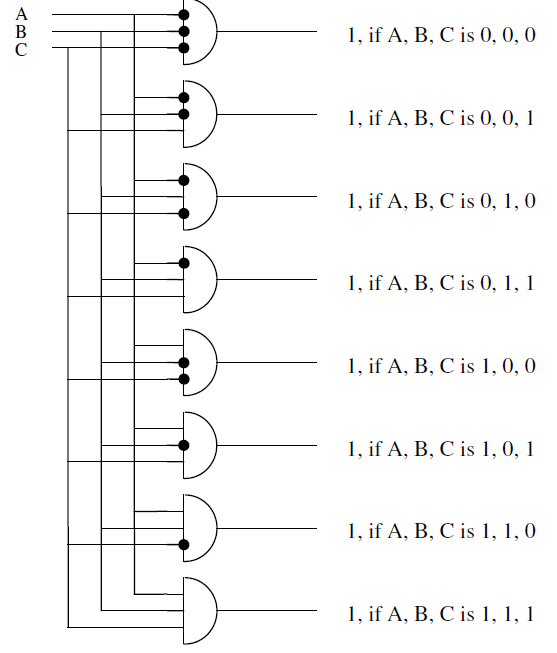
3.12 三输入译码器
3.13
五输入译码器有 2 5 = 32 2^5=32 25=32 根输出线
3.14
2 4 = 16 2^4=16 24=16 所以16输入多路选择器有4条选择线
3.15 全加器

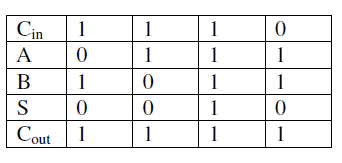
A=7,B=11,A+B=18=10010
最高位有进位,发生溢出
3.16
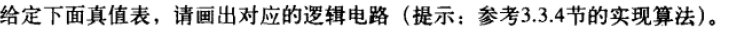
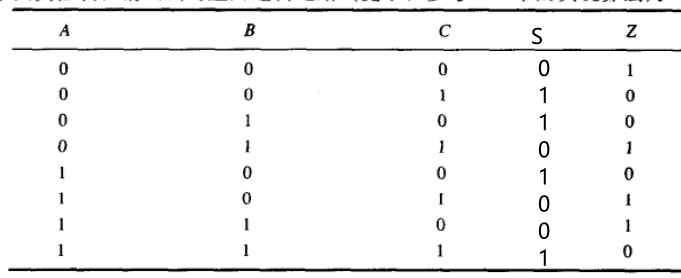
相当于全加器本位运算结果
S = A ⊕ B ⊕ C S=A\oplus B\oplus C S=A⊕B⊕C
Z = S ‾ = S = A ⊕ B ⊕ C ‾ Z=\overline{S}=\overline{S=A\oplus B\oplus C} Z=S=S=A⊕B⊕C
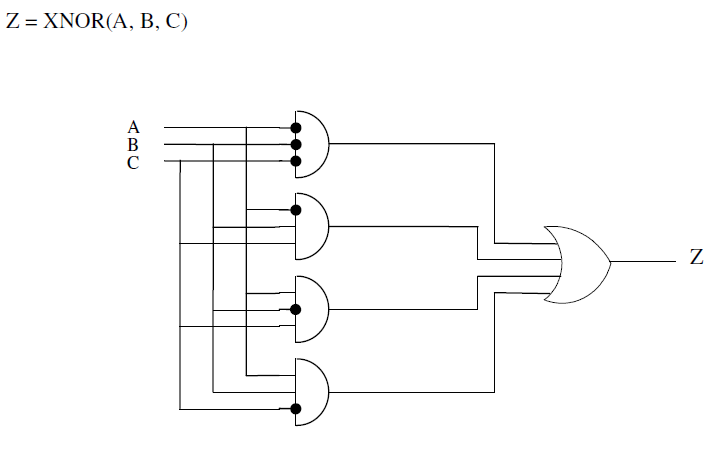
3.17

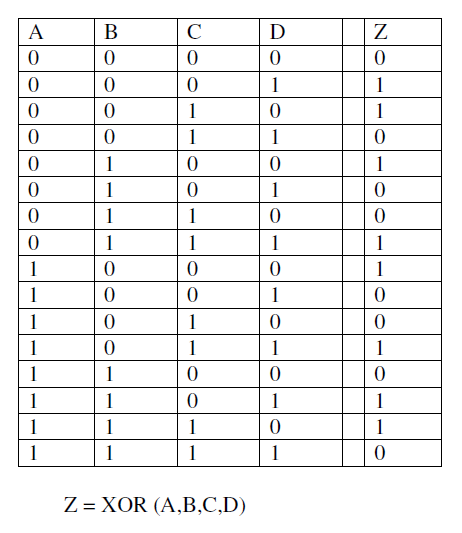
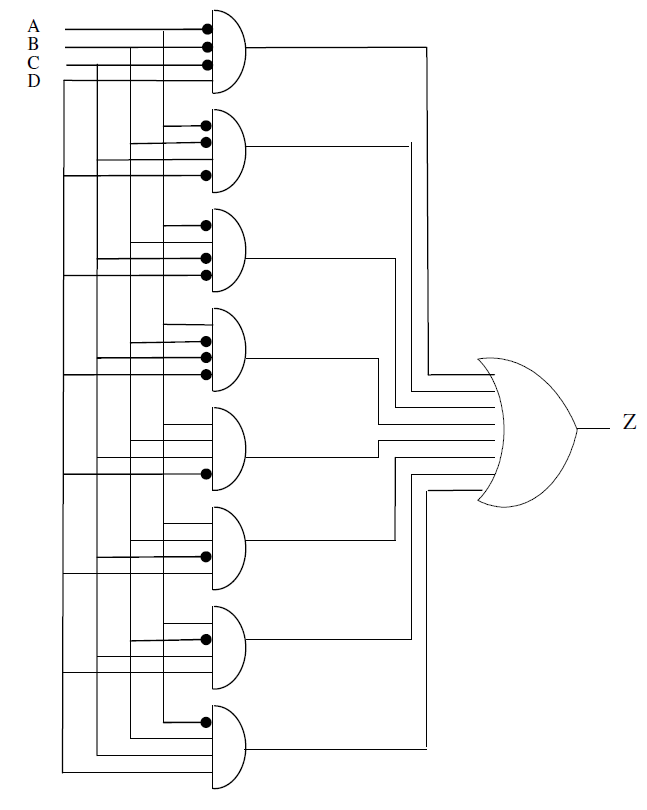
3.18 与或非门PLA

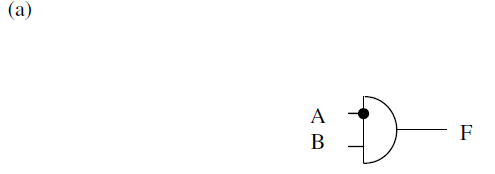
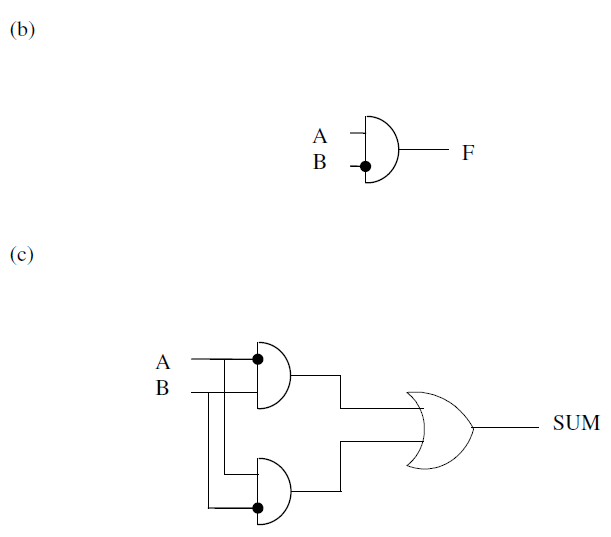
(d) 缺少进位信息
3.19
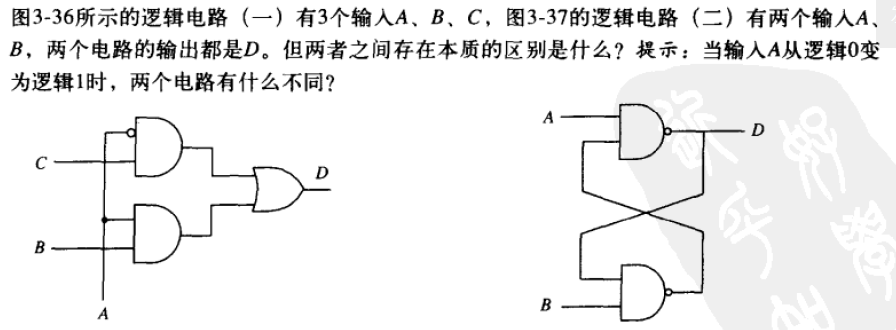
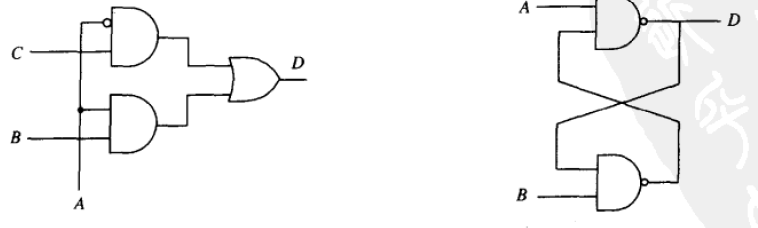
A图是时序逻辑,B图是R-S锁存器
时序逻辑电路输出仅与当前输入有关
R-S锁存器,在A=B=1时,处于静止状态
- A=0,置1
- B=0,置0
3.20

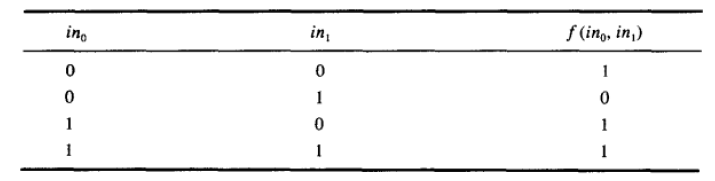
三同一异 与门相关
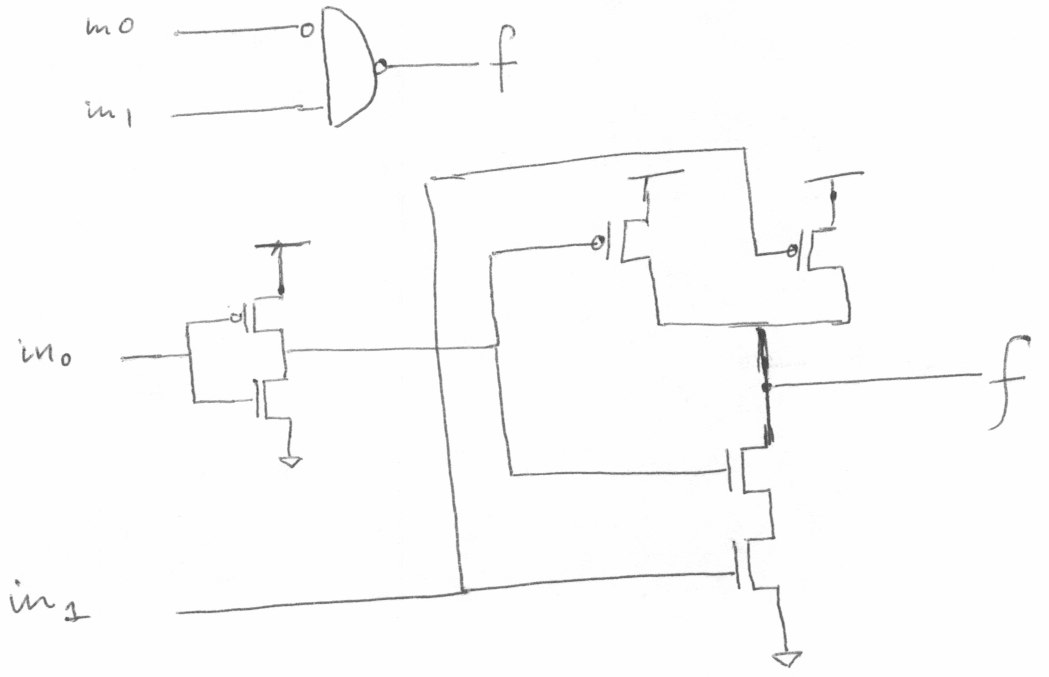
3.21

2 × 2 14 = 2 15 2\times 2^{14}=2^{15} 2×214=215 个半子
3.22

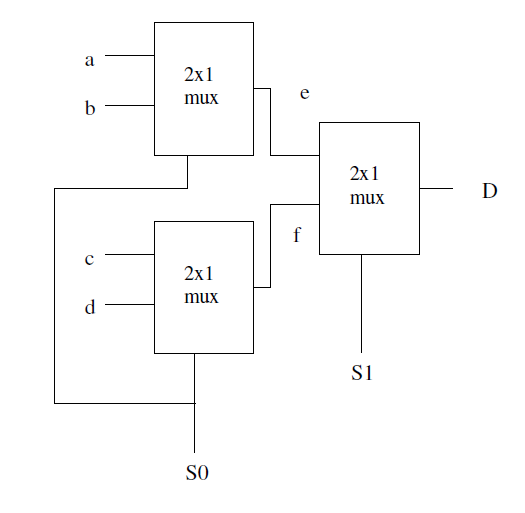
S 1 S_1 S1 为片选信号, S 0 S_0 S0 为片内信号

3.23
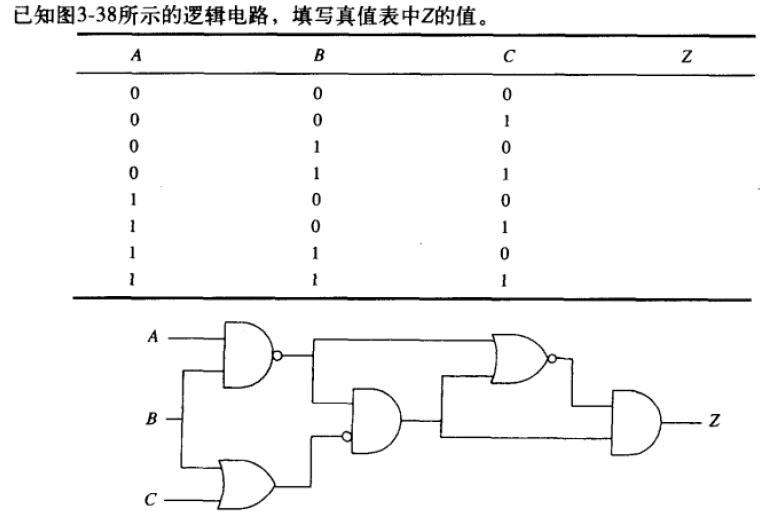
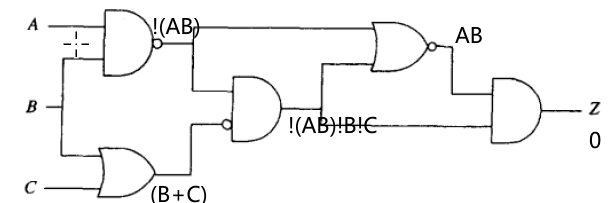
A B ‾ ⋅ B ‾ ⋅ C ‾ + A B ‾ ‾ = A B + ( A B ‾ + 1 ) ‾ = A B \overline{\overline{AB}\cdot \overline{B}\cdot \overline{C}+\overline{AB}}=AB+ \overline{(\overline{AB}+1)}=AB AB⋅B⋅C+AB=AB+(AB+1)=AB
3.24
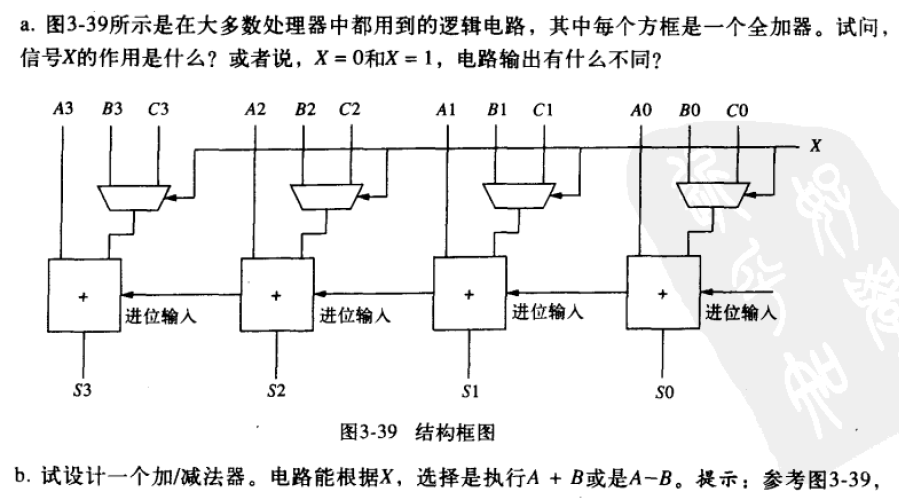
选通:
X=0,S=A+B
X=1,S=A+C
可令 C = B ‾ , C a r r y i n = X C=\overline{B},Carry_{in}=X C=B,Carryin=X
3.25

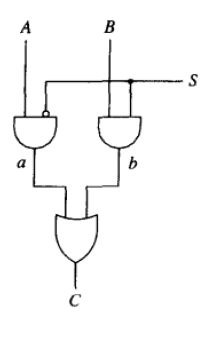
1非1与1或,有三个门延迟
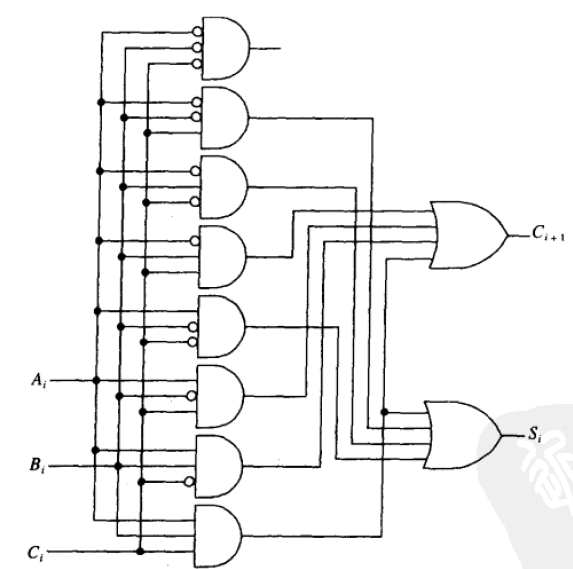
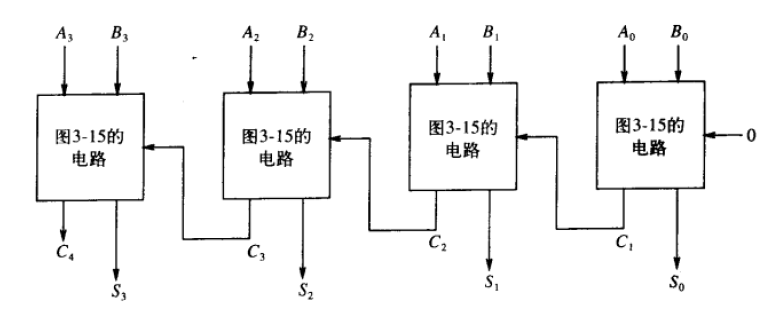
- 1bit加法器有3个门延迟,所以四个1bit加法器串联有12个门延迟
扩展为32位全加器,传输延迟为 32 × 3 = 96 32\times 3=96 32×3=96 个
3.26
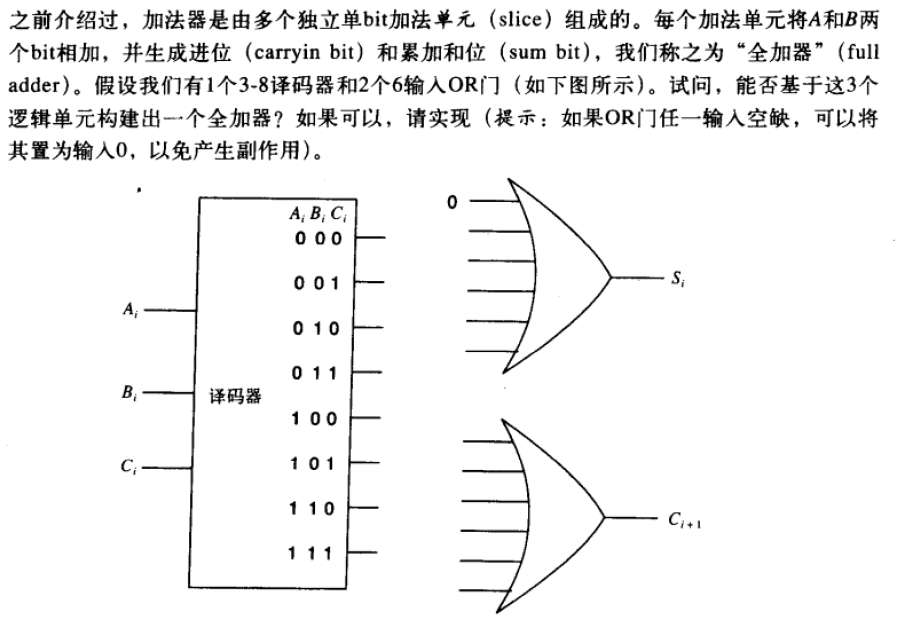
S=1:单数个1
C=1:2个1或三个1
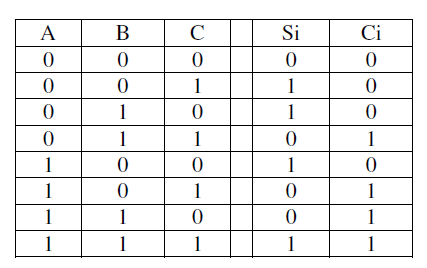
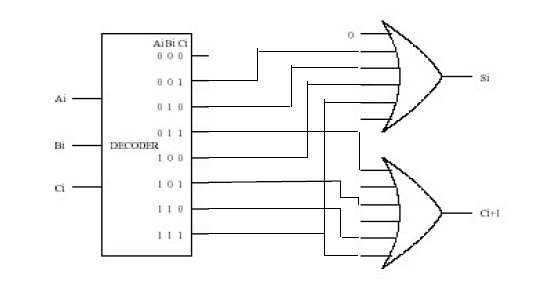
3.27
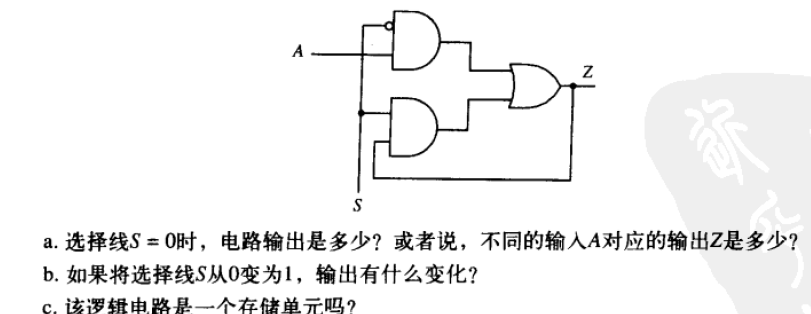
S=0,Z=A
S=1,Z不变,存储之前的值。是一个存储单元
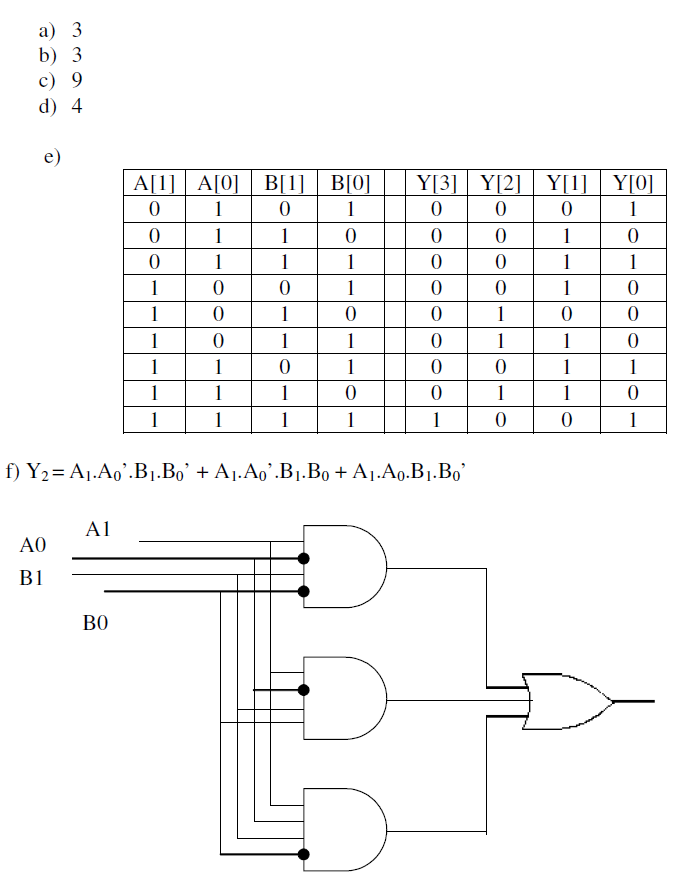
3.29

存储单元是覆盖式的,一旦被写入就无法恢复
3.30
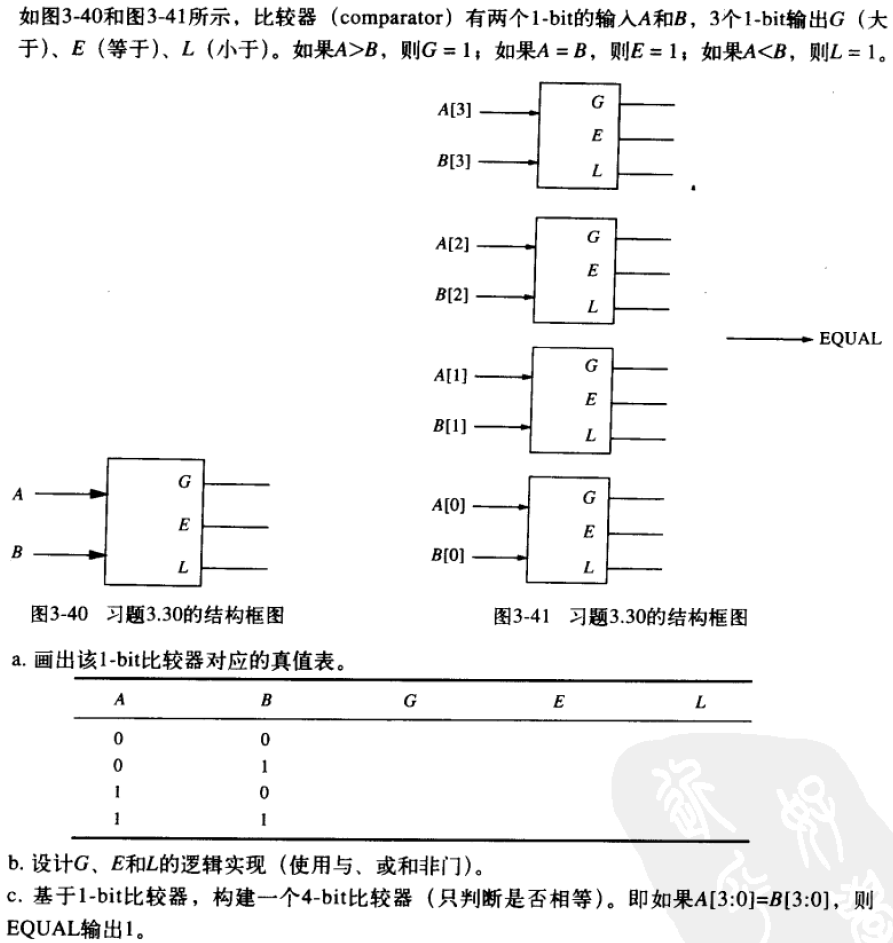
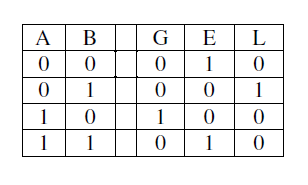
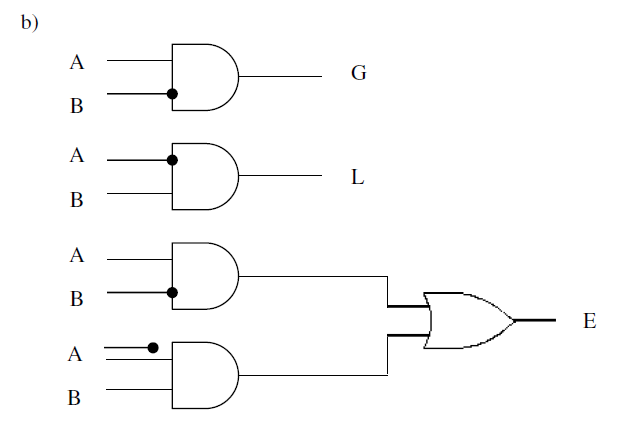
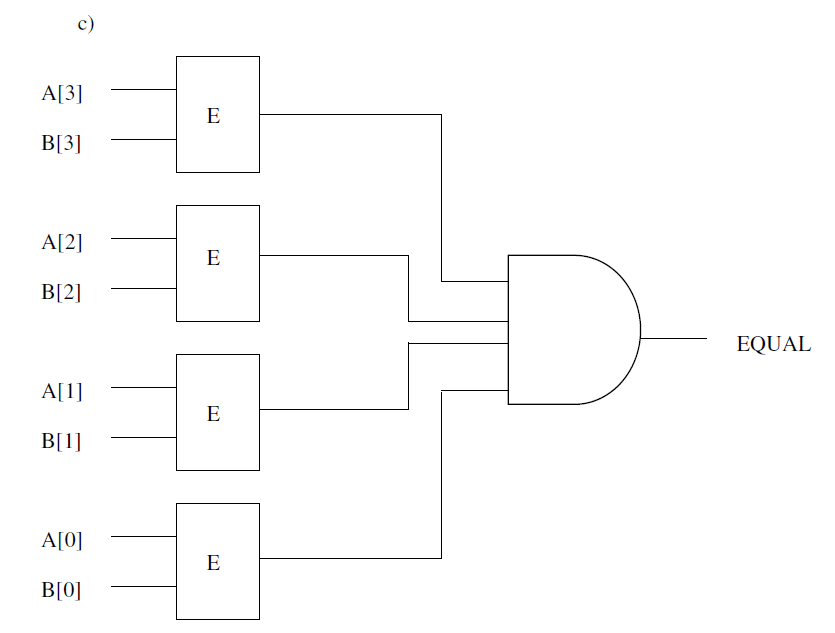
2 3 ⋅ 8 B = 64 B 2^3\cdot 8B=64B 23⋅8B=64B
3.32
内存地址指向一个存储字的位置
内存寻址能力是一个存储字的存储字长,一个存储字中有多少bit
3.33

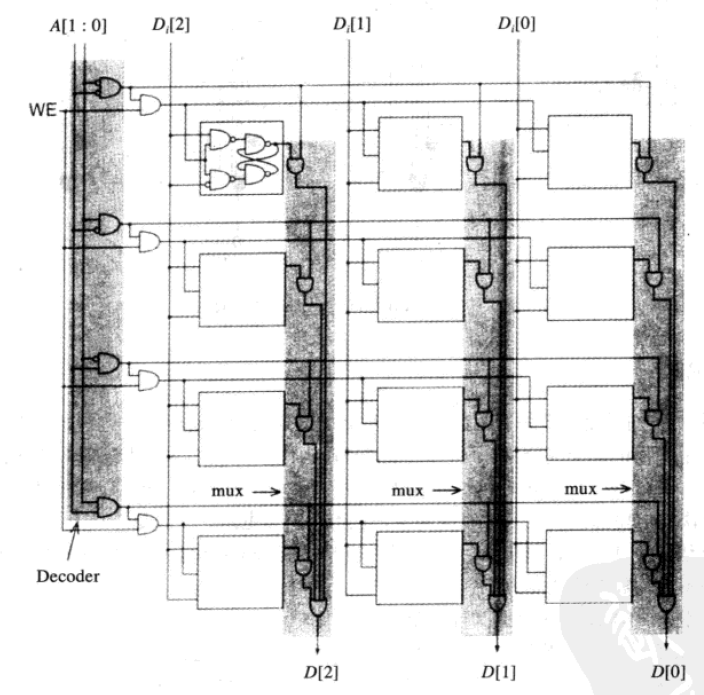

3.34
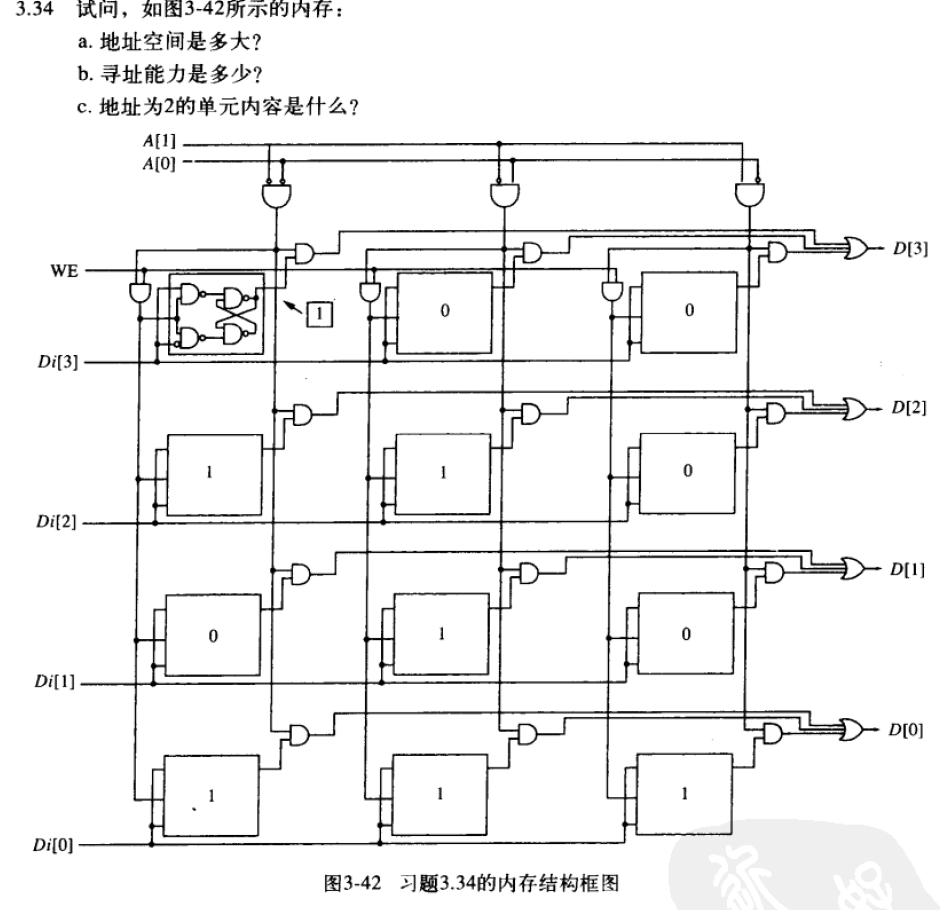

3.35
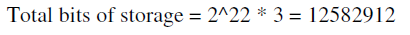
3.36

组合逻辑,无存储功能,输出只与当前输入有关




3.41

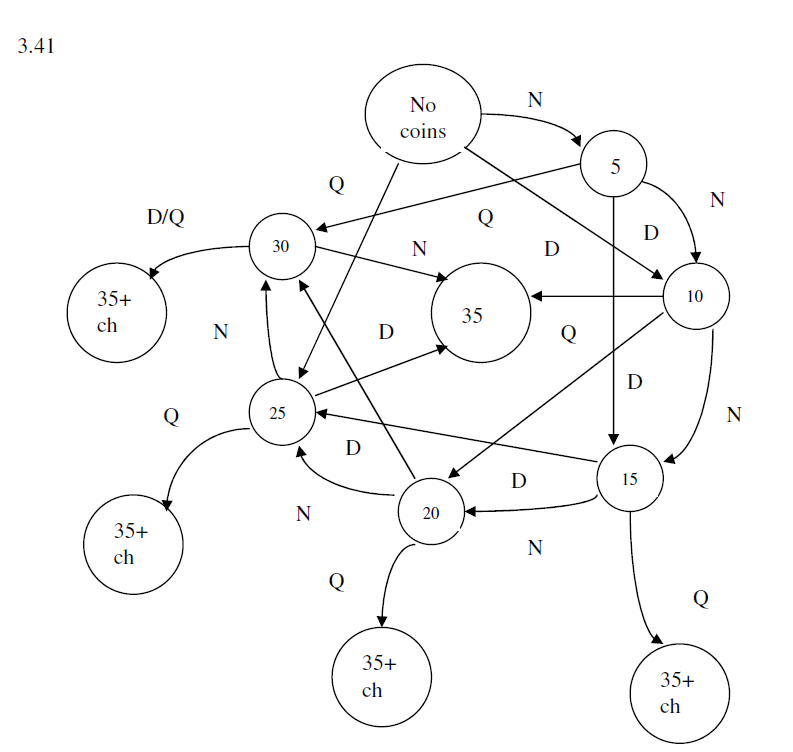
三种输入:
N:投5美分
D:投10美分
Q:投25美分
9种状态
2种输出
- 只输出汽水
- 输出汽水并找零
3.43
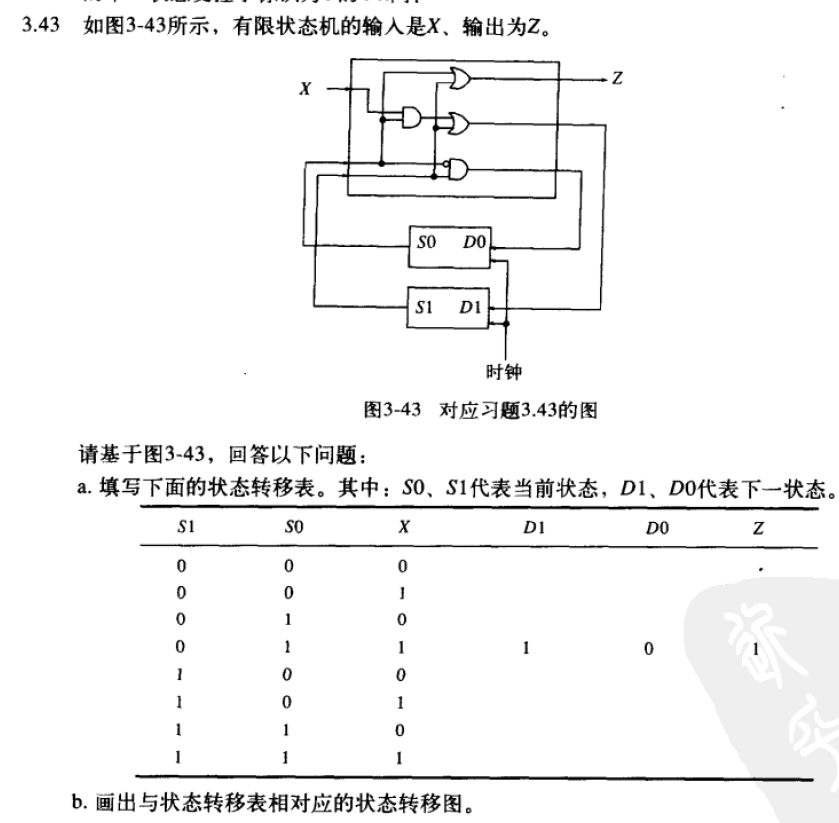
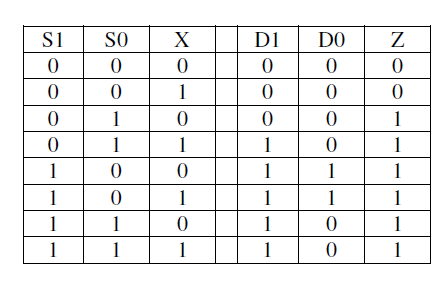
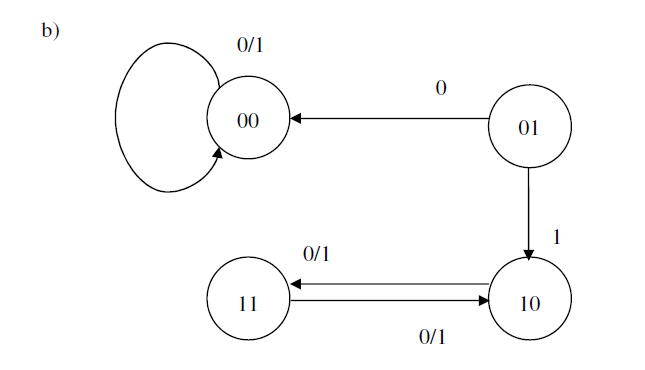
3.43

即用与非门构造与或非三种逻辑门
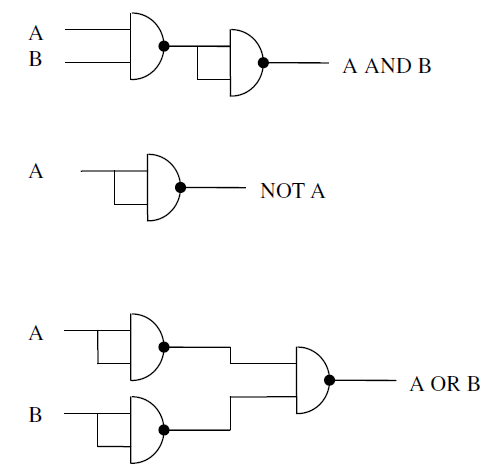
A B = A B ‾ ⋅ A B ‾ ‾ AB=\overline{\overline{AB}\cdot \overline{AB}} AB=AB⋅AB
A ‾ = A ⋅ A ‾ \overline{A}=\overline{A\cdot A} A=A⋅A
A + B = A ‾ ⋅ B ‾ ‾ A+B=\overline{\overline{A}\cdot \overline{B}} A+B=A⋅B