在人工智能领域,比如深度学习,机器学习,张量这一概念被频繁使用。虽然网上有很多关于张量的文章,但基本都是废话太多,而且复制粘贴说不到重点。
今天我就来讲解一下张量维度的真正含义。
首先. 张量并不是一个简单多维数组的概念
为了说明这个问题,用代码解释最为清楚(这里用pytorch作为演示工具):
>>> import torch
>>> torch.rand(2,3,4)tensor([[[0.3893, 0.0926, 0.5927, 0.0362],
[0.7488, 0.1284, 0.1658, 0.6883],
[0.9692, 0.6096, 0.3811, 0.6348]],[[0.3132, 0.4856, 0.5010, 0.5382],
[0.4209, 0.9758, 0.6052, 0.8183],[0.0462, 0.9005, 0.9736, 0.8771]]])
我不知道各位有没有从上面的例子,发现到规律没有?
(2,3,4)是上面这个张量的形状没错,但是这不是重点。重点在于: 你怎么去理解这个维度在上面数组中的具体含义的?
首先我给出一个结论:在多维张量中,张量维度中的最后一个维度表示了张量的最小单位,也是该最小单位的列数/长度。
我相信:这是网上从来没有人告诉过你的一个关键特征。因为他们都不懂,要么就是故意不说
你可以看到上面这个三维张量的最小单位:[0.3893, 0.0926, 0.5927, 0.0362],它的列数刚好是4
为了印证这一点,我把上面的张量从3维扩展4维:
>>> torch.rand(2,3,4,5)
tensor([[[[0.2797, 0.8020, 0.4698, 0.5959, 0.3229],
[0.9926, 0.6175, 0.1324, 0.1322, 0.6438],
[0.2046, 0.3593, 0.8734, 0.1032, 0.4316],
[0.2191, 0.5165, 0.7173, 0.2843, 0.7192]],[[0.7188, 0.9162, 0.7454, 0.0712, 0.0822],
[0.3084, 0.4359, 0.3200, 0.6938, 0.8972],
[0.8860, 0.0275, 0.9120, 0.9609, 0.4668],
[0.3209, 0.4625, 0.6925, 0.3628, 0.5243]],[[0.5671, 0.5452, 0.8791, 0.0238, 0.9310],
[0.9554, 0.4225, 0.1282, 0.0430, 0.1930],
[0.3095, 0.3146, 0.7911, 0.9851, 0.0080],
[0.6860, 0.2170, 0.0167, 0.3191, 0.1569]]],
[[[0.0101, 0.4069, 0.0368, 0.0711, 0.8693],
[0.6945, 0.0231, 0.6840, 0.1747, 0.9457],
[0.8171, 0.0382, 0.4268, 0.0348, 0.0104],
[0.9574, 0.7956, 0.6939, 0.1443, 0.4272]],[[0.2437, 0.0244, 0.6358, 0.7854, 0.5776],
[0.8892, 0.5903, 0.3915, 0.0739, 0.8040],
[0.1287, 0.8313, 0.2242, 0.3242, 0.6272],
[0.5183, 0.3957, 0.9779, 0.7776, 0.5292]],[[0.4206, 0.0818, 0.5058, 0.9838, 0.7958],
[0.1617, 0.9986, 0.8095, 0.8501, 0.9051],
[0.3168, 0.5005, 0.6576, 0.3395, 0.0077],
[0.5153, 0.1495, 0.5506, 0.5251, 0.3986]]]])
同样可以看到这个四维张量的最小单元:[0.2797, 0.8020, 0.4698, 0.5959, 0.3229]
它的列数/长度是5,跟它的形状(2,3,4,5)中最后一个维度刚好对应。
所以,首先多维张量的维度一定要倒过来看!
那么这个4维张量的这么中括号,我们该从哪里看起呢?
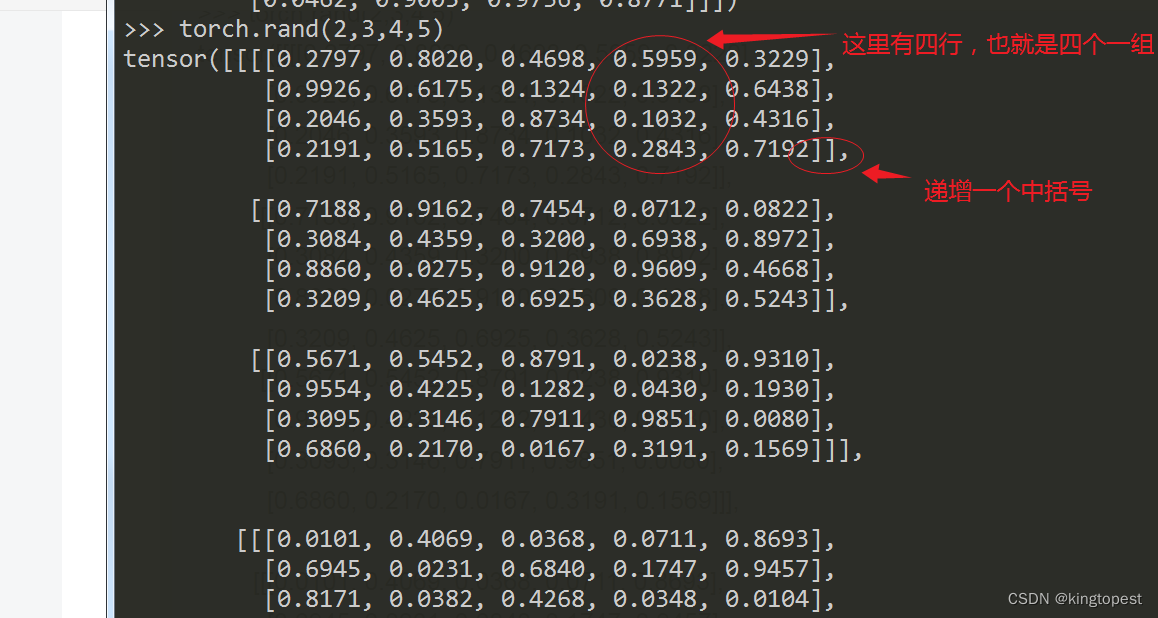
从上面的图片中可以看到端倪:
在两个中括号包围的里面: 以张量最小单位,四个为一组。4刚好是倒数第二维度4的大小。
所以,每递增一个中括号,当前维度就会逆向往上递增一个维度。
注意: 这里维度都是倒过来看的
现在继续递增中括号==》
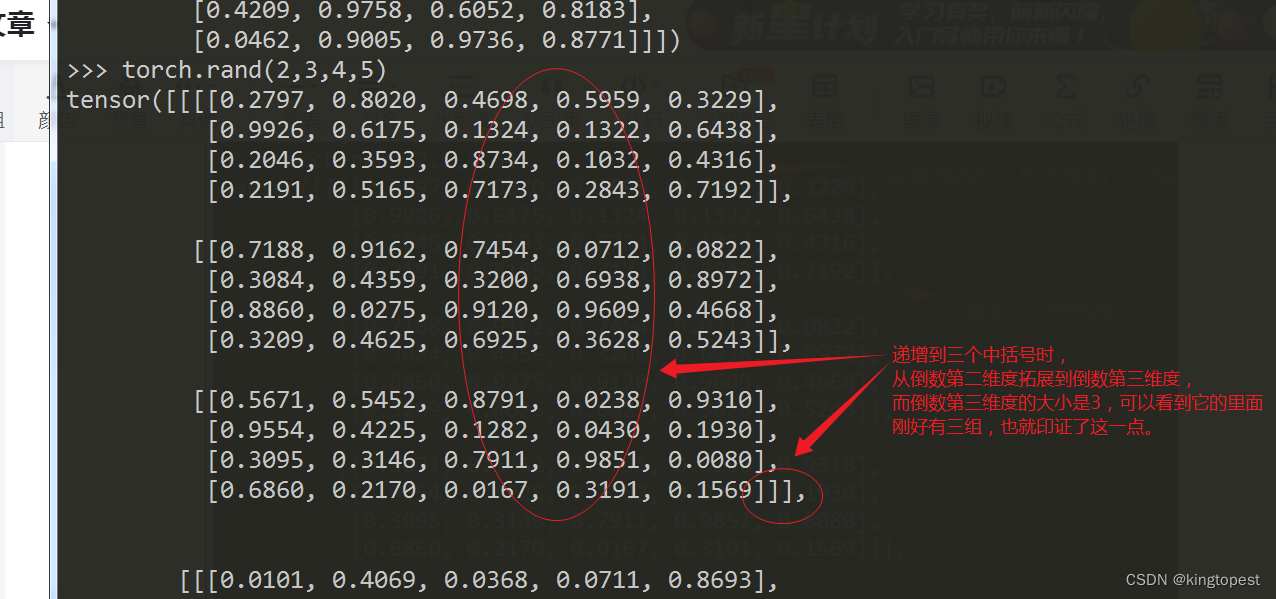
可以看到当中括号递增到第三层时,它的里面刚好有3组,也就是倒数第三维度的大小。
如果我们继续往上递增维度呢?
此时可以看到因为上面的三个中括号后面有个逗号,说明有个后面的同级的三维。
那总共有几个呢?需要继续升维。
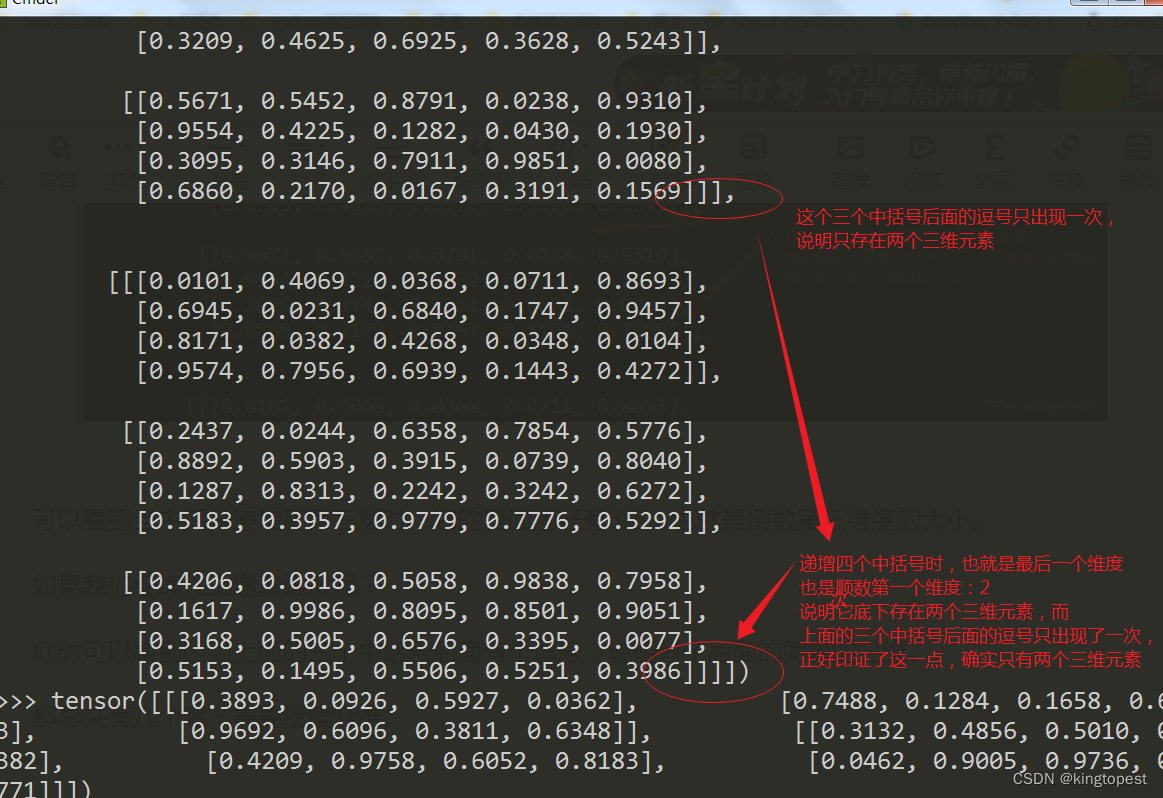
当递增到四个中括号时,也就是倒数最后一个维度,也是顺数第一维度:2
说明它底下存在两个三维元素。而上面的三个中括号后面的逗号只出现过一次,正好印证了这一点,确实只有两个三维元素。
所以,关于张量的维度总结起来有以下几点:
1. 在多维张量中,张量维度中的最后一个维度表示了张量的最小单位,也是该最小单位的列数/长度。
2. 张量的维度应该倒过来看,而且每递增一个中括号,当前维度就会逆向往上递增一个维度。
3. 张量当前维度大小的意义: 表示它子维度成员的数量
再举一个张量实际应用的例子:
比如以下图像张量:
(samples, height, width,channel, colorDepth)
这个张量代表了:图像样本的数量,图像样本的长,宽,色彩通道以及色深。





![[MySql]表的增删查改](https://img-blog.csdnimg.cn/260f16477e8245b991584552c6d6e1c2.png)