参考文档：

曲柄滑块机构运动分析..doc-原创力文档

偏置曲柄滑块机构的运动学分析 - 豆丁网

偏置式曲柄滑块机构仿真与运动分析 - 豆丁网

https://www.cnblogs.com/aksoam/p/17013811.html

function main
%输入已知数据
close all
clear;
i1=100;
i2=300;
e=56;
hd = pi/180; %一度对应的弧度
du=180/pi;  %一弧度对应的度数
omega1=10;  %主动件角速度
alpha1=0;   %主动件角加速度
 
%使用子函数计算出曲柄滑块的位置，速度，加速度。
for n1=1:721
    theta1(n1)=(n1-1)*hd;          %
    %调用函数
    [theta2(n1),xc(n1),omega2(n1),vc(n1),alpha2(n1),ac(n1)]=sli_crank(theta1(n1),omega1,alpha1,i1,i2,e);
end
%图形输出
figure;
%绘制位移的图
[ax,h1,h2]=plotyy(theta1*du,theta2*du,theta1*du,xc);
set(get(ax(1), 'ylabel'), 'String', '连杆角位移/\circ');
set(get(ax(2), 'ylabel'), 'String', '滑块位移/mm');
title('位移图');
xlabel('曲柄转角\theta_1/\circ');


%速度
figure
[ax,h1,h2]=plotyy(theta1*du,omega2,theta1*du,vc)
title('速度图');
xlabel('曲柄转角\theta_1/\circ')
ylabel('连杆角速度/rad\cdots^{-1}')

 
%加速度
figure
[ax,h1,h2]=plotyy(theta1*du,alpha2,theta1*du,ac)
title('加速度图');
xlabel('曲柄转角\theta_1/\circ')
ylabel('连杆角加速度/rad\cdots^{-2}')

figure
j=0;
for n1 = 1:5:360
    j=j+1;
    clf;
    x(1)=0;
    y(1)=0;
    x(2)=i1*cos(n1*hd);
    y(2)=i1*sin(n1*hd);
    x(3)=xc(n1);
    y(3)=e;
    x(4)=i1+i2+50;
    y(4)=0;
    x(5)=0;
    y(5)=0;
    x(6)=x(3)-40;
    y(6)=y(3)+10;
    x(7)=x(3)+40;
    y(7)=y(3)+10;
    x(8)=x(3)+40;
    y(8)=y(3)-10;
    x(9)=x(3)-40;
    y(9)=y(3)-10;
    x(10)=x(3)-40;
    y(10)=y(3)+10;
    i=1:3;
    plot(x(i), y(i));
    grid on;
    hold on;
    i=4:5;
    plot(x(i), y(i))
    i=6:10;
    axis equal
    plot(x(i), y(i))
    plot(x(1),y(1),'o')
    plot(x(2),y(2),'o')
    plot(x(3),y(3),'o')
    text(-10,-10,'A')
    text(x(2)-15,y(2)+10,'B')
    text(x(3),y(3)-20,'C')
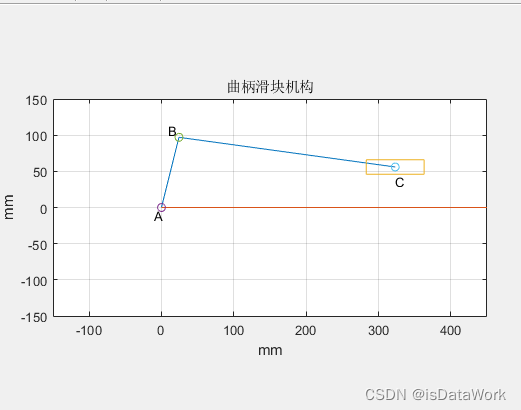
    title('曲柄滑块机构');
    xlabel('mm');
    ylabel('mm');
    axis([-150 450 -150 150]);
    m(j)=getframe;
end
movie(m,2);
end
 
%返回连杆和滑块的参数
function[theta2,xc,omega2,vc,alpha2,ac]=sli_crank(theta1,omega1,alpha1,i1,i2,e)
 
    %计算连杆的角位移theta2和xc
    theta2=asin((e-i1*sin(theta1))/i2);
    xc=i1*cos(theta1)+i2*cos(theta2);
 
    %计算连杆和滑块的参数
    A=[ i2*sin(theta2),1;
        -i2*cos(theta2),0
        ];
    B=[-i1*sin(theta1);
    i1*cos(theta1)];
    omega=A\(omega1*B);
    omega2=omega(1);
    vc=omega(2);
    
    %计算连杆和滑块的加速度
    AT=[
        omega2*i2*cos(theta2),0;
        omega2*i2*sin(theta2),0
        ];
    BT=[
        -omega1*i1*cos(theta1);
        -omega1*i1*sin(theta1)
    ];
    alpha=A\(-AT*omega+alpha1*B+omega1*BT);
    alpha2=alpha(1);
    ac=alpha(2);
end