下降路径最小和

力扣链接：931. 下降路径最小和

题目描述

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例

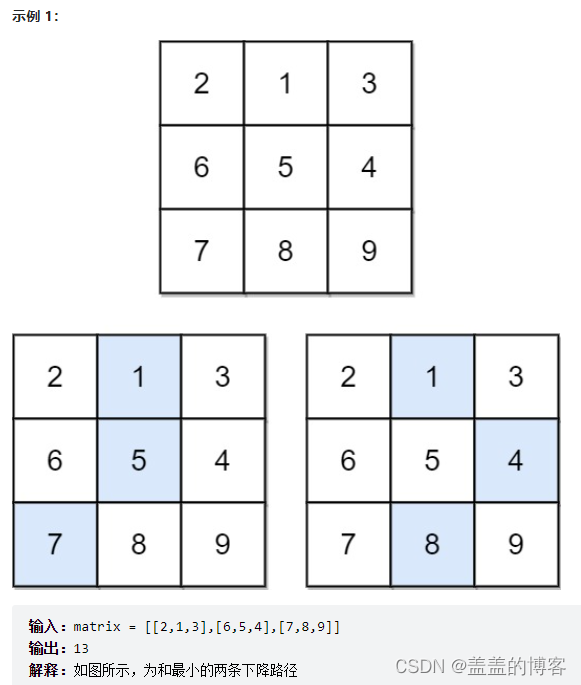
Java代码

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        int n = matrix.length, res = Integer.MAX_VALUE;
        for(int i = 1; i < n; i++) {
            for(int j = 0; j < n; j++) {
                if(j == 0) {
                    matrix[i][j] += Math.min(matrix[i - 1][j], matrix[i - 1][j + 1]);
                }else if(j == n - 1) {
                    matrix[i][j] += Math.min(matrix[i - 1][j - 1], matrix[i - 1][j]);
                }
                else {
                    matrix[i][j] += Math.min(matrix[i - 1][j - 1], Math.min(matrix[i - 1][j], matrix[i - 1][j + 1]));
                }
            }
        }
        for(int j = 0; j < n; j++) {
            res = Math.min(res, matrix[n - 1][j]);
        }
        return res;
    }
}

python代码

class Solution:
    def minFallingPathSum(self, matrix: List[List[int]]) -> int:
        dp = [matrix[0]]
        n = len(matrix)
        for i in range(1, n):
            cur = [0] * n
            for j in range(n):
                mn = dp[-1][j]
                if j > 0:
                    mn = min(mn, dp[-1][j - 1])
                if j < n - 1:
                    mn = min(mn, dp[-1][j + 1])
                cur[j] = mn + matrix[i][j]
            dp.append(cur)
        return min(dp[-1])

---

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/minimum-falling-path-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。