上一话
分割2——语义分割评价指标
https://blog.csdn.net/XiaoyYidiaodiao/article/details/125149509?spm=1001.2014.3001.5502
转置卷积不是卷积的逆操作，并且转置卷积是卷积操作！
这是因为普通卷积的操作图 1.
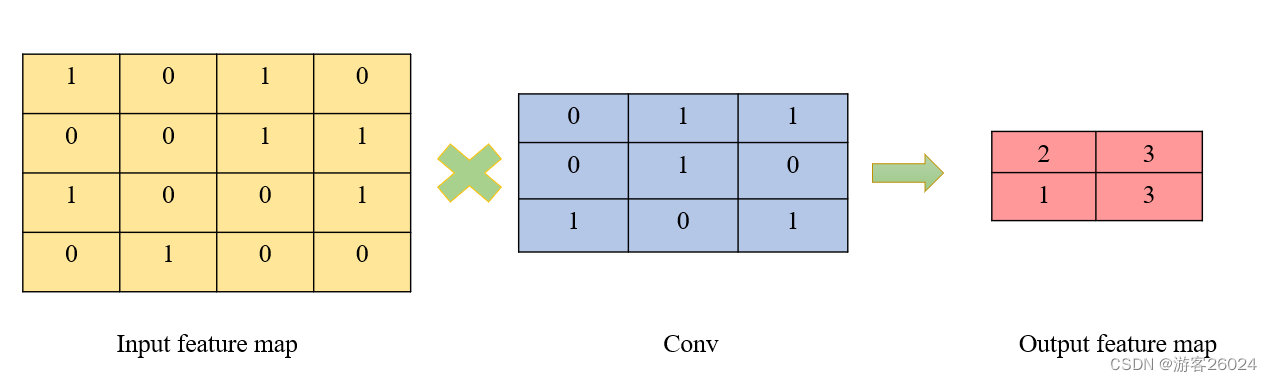
其卷积可等效为图 2.
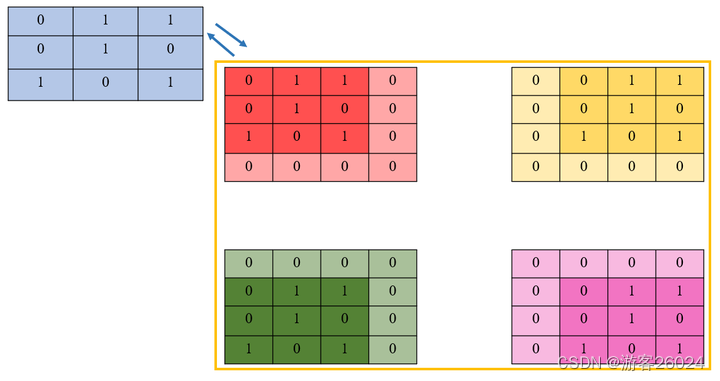
其卷积操作可等效为图 3.
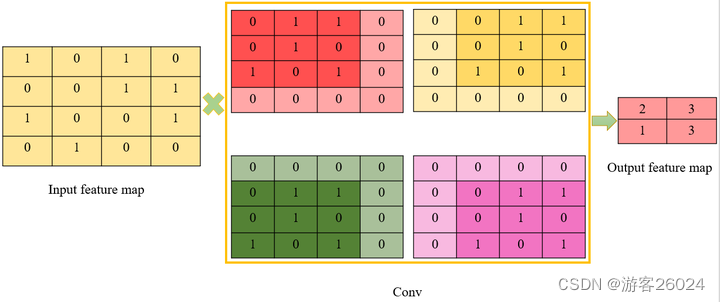
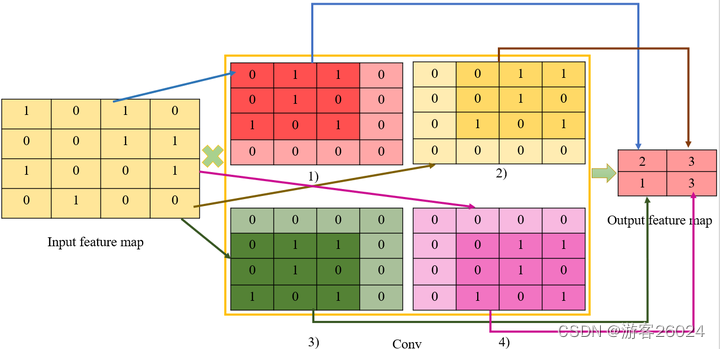
图 2. 卷积 还可等效为图 4. 扩展为图 5. -> 图 6.
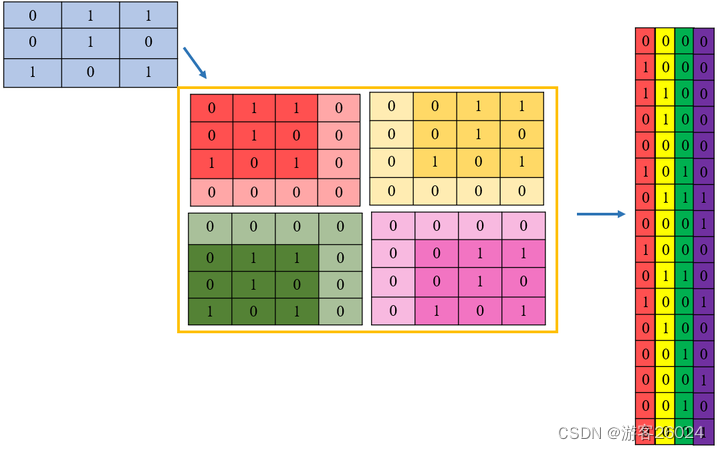
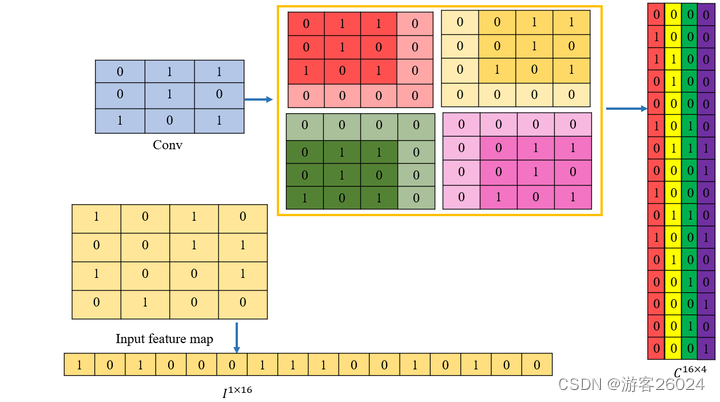
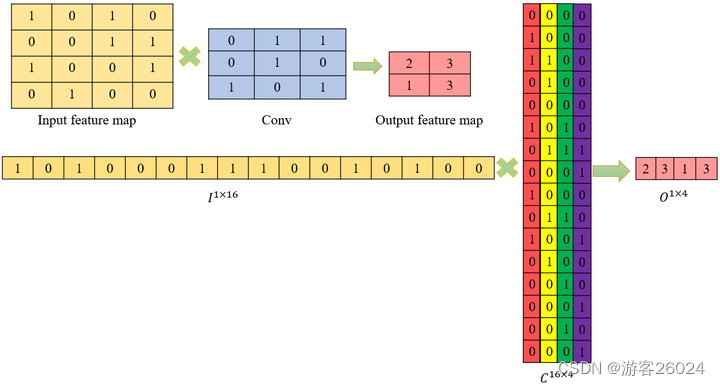
输入特征图、卷积与输出特征图展平后可整理成：
接下来出现一个问题，已知矩阵与矩阵
能否反向求得矩阵
答案是不能。当然，如果能在等号左右两边乘上的逆矩阵，则能反向求得矩阵
；但是一个矩阵能有逆矩阵的前提条件是此矩阵必是方阵，但是
不为方阵，则不能反向求得
（没法通过矩阵
与矩阵
还原矩阵
）。
这样也就说明了转置卷积并不是卷积的逆操作！并且也说明了一般情况下，卷积不可逆！
接下来，放宽条件，我们只想通过 与
得到一个与
大小相同的矩阵，能行吗？
答案是能行。只需要在等号左右两边乘上矩阵 的转置 (
) 即可！
且
此时的这个我们reshape成
的矩阵, 便是我们真正的转置矩阵，也就是我们所说的转置卷积，
可以是
上下左右翻转得到！
参考文献
转置卷积https://www.bilibili.com/video/BV1mh411J7U4/?spm_id_from=333.788
下一话
FCN
未完...
