---

引言

本系列为 CMU 15-445 Fall 2022 Database Systems 数据库系统 [卡内基梅隆] 课程重点知识点摘录，附加个人拙见，同样借助CMU 15-445课程内容来完成MIT 6.830 lab内容。

---

Sorting

为什么需要排序

需要排序算法的原因：本质在于 tuples 在 table 中没有顺序，无论是用户还是 DBMS 本身，在处理某些任务时希望 tuples 能够按一定的顺序排列，如：

• 若 tuples 已经排好序，去重操作将变得很容易（DISTINCT)
• 批量将排好序的 tuples 插入到 B+ Tree index 中，速度更快
• Aggregations (GROUP BY)

Algorithms

若数据能够放入内存中，我们可以使用标准排序算法搞定，如快排；若数据无法放入内存中，就得考虑数据在 disk 与 memory 中移动的成本，以及排序算法的适配。

External Merge Sort

外部排序通常有两个步骤：

• Sorting Phase：将数据分成多个 chunks，每个 chunk 可以完全读入到 memory 中，在 memory 中排好序后再写回到 disk 中
• Merge Phase：将多个子文件合并成一个大文件

2-Way External Merge Sort

以下是 2-way external merge sort 的一个简单例子，假设：

• Files 本分成 N 个 pages
• DBMS 有 B 个 fixed-size buffers

Pass #0

• 从 table 中读入 B pages tuples
• 将这些 tuples 排序后写会到 disk 中
• 每一轮成为一个 run

Pass #1,2,3,…

• 递归地将一对 runs 合并成一个两倍长度的 run
• 这一操作值需要 3 个 buffer pages ( 2 个用于输入，1个用于输出)
  
  完整过程如下图所示：
  

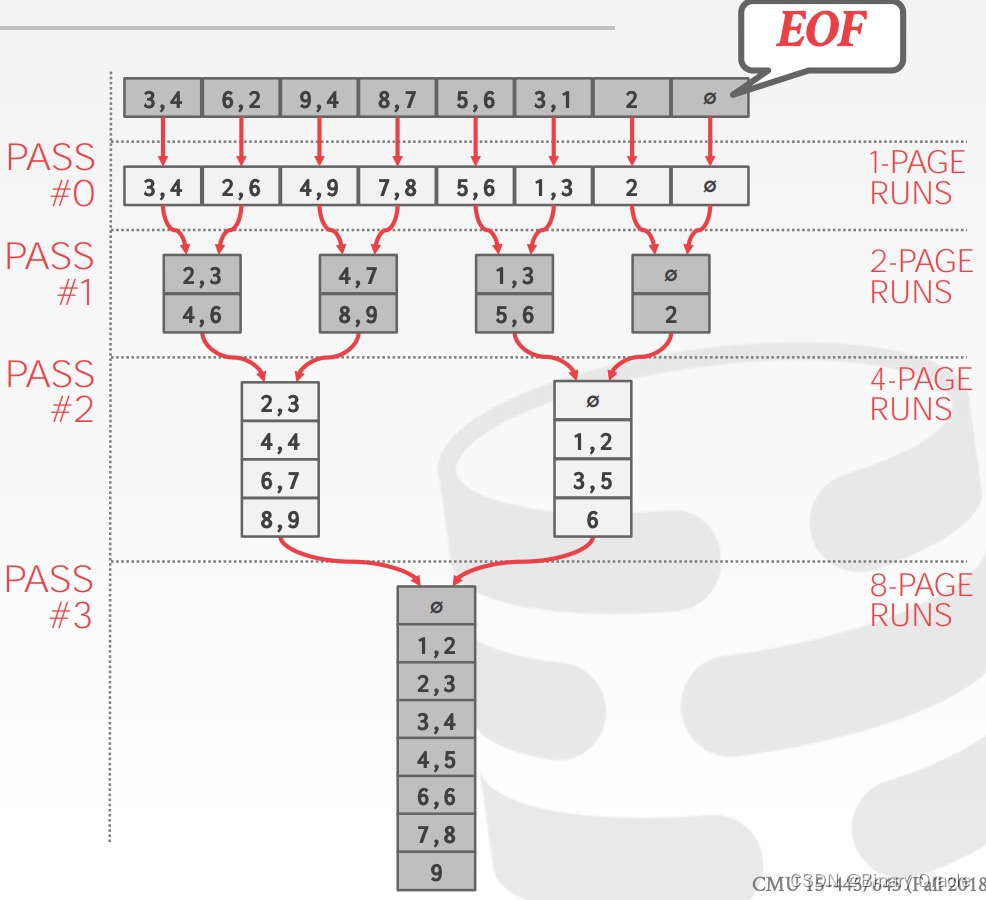
归并排序再数据库中的玩法

复杂度：

• number of passes：1+ceil(log2N)
• cost/pass：I/O 成本为 2N ，系数 2 表示读入 + 写出。
• total cost： 2N × (number of passes)

值得注意的是：

• 这个算法只需要 3 个 buffer pages，B=3
• 即使 DBMS 能够提供更多的 buffer pages（B>3），2-way external merge sort 也无法充分地利用它们

如何能够利用到更多的 buffer pages ？

---

General External Merge Sort

将以上的 2-way external merge sort 泛化成 N-Way 的形式：

Pass #0

• 使用 B 个 buffer pages
• 产生 ceil(N/B) 个大小为 B 的 sorted runs

Pass #1,2,3,…

• 合并 B-1 runs

复杂度：

• number of passes： 1+ceil(logB−1 ceil(N/B))
• cost/pass： 2N
• total cost： 2N × (number of passes)

---

实例：Sort 108 pages file with 5 buffer pages：N = 108, B = 5

• Pass #0: ceil(108/5) = 22 sorted runs of 5 pages each
• Pass #1: ceil(22/4) = 6 sorted runs of 20 pages each
• Pass #2: ceil(6/4) = 2 sorted runs of 80 pages and 28 pages each
• Pass #3: sorted file of 108 pages

一共有 1+ceil(logB−1 ceil(N/B)) = 1+ceil(log4 22) = 4 passes

---

Using B+ Trees

如果被排序的表在对应的 attribute(s) 上已经建有索引，我们就可以用它来加速排序的过程，按照目标顺序遍历 B+ Tree 的 leaf pages 即可，但这里要注意有两种情况：

• Clustered B+ Tree
• Unclustered B+ Tree

case 1: Clustered B+ Tree

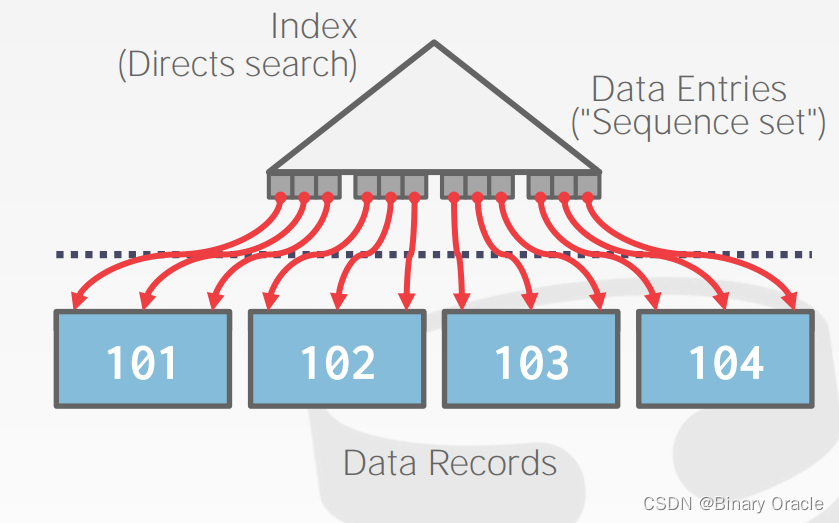
这种情况永远由于 external sorting。

case 2: Unclustered B+ Tree

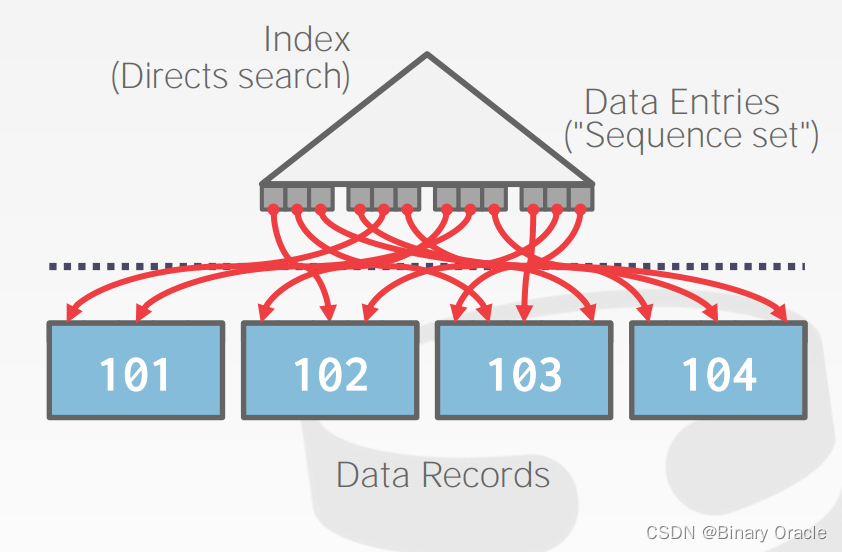
这是最糟糕的情况，因为获取每个 data record 的过程都可能需要一次 I/O。

其实就是聚集索引和非聚集索引的区别，非聚集索引涉及到回表查询，效率会低一些，但是占据空间大小少很多。

---

Aggregations

aggregation 就是对一组 tuples 的某些值做统计，转化成一个标量，如平均值、最大值、最小值等，aggregation 的实现通常有两种方案：

• Sorting
• Hashing

Sorting Aggregation

但很多时候我们并不需要排好序的数据，如：

• Forming groups in GROUP BY
• Removing duplicates in DISTINCT

在这样的场景下 hashing 是更好的选择，它能有效减少排序所需的额外工作。

---

Hashing Aggregation

利用一个临时 (ephemeral) 的 hash table 来记录必要的信息，即检查 hash table 中是否存在已经记录过的元素并作出相应操作：

• DISTINCT: Discard duplicate
• GROUP BY: Perform aggregate computation

如果所有信息都能一次性读入内存，那事情就很简单了，但如若不然，我们就得变得更聪明。

hashing aggregation 同样分成两步：

• Partition Phase: 将 tuples 根据 hash key 放入不同的 buckets
  • use a hash function h1 to split tuples into partitions on disk
    • all matches live in the same partition
    • partitions are “spilled” to disk via output buffers
  • 这里有个额外的假设，即每个 partition 能够被放到 memory 中
• ReHash Phase: 在内存中针对每个 partition 利用 hash table 计算 aggregation 的结果

如下图所示：

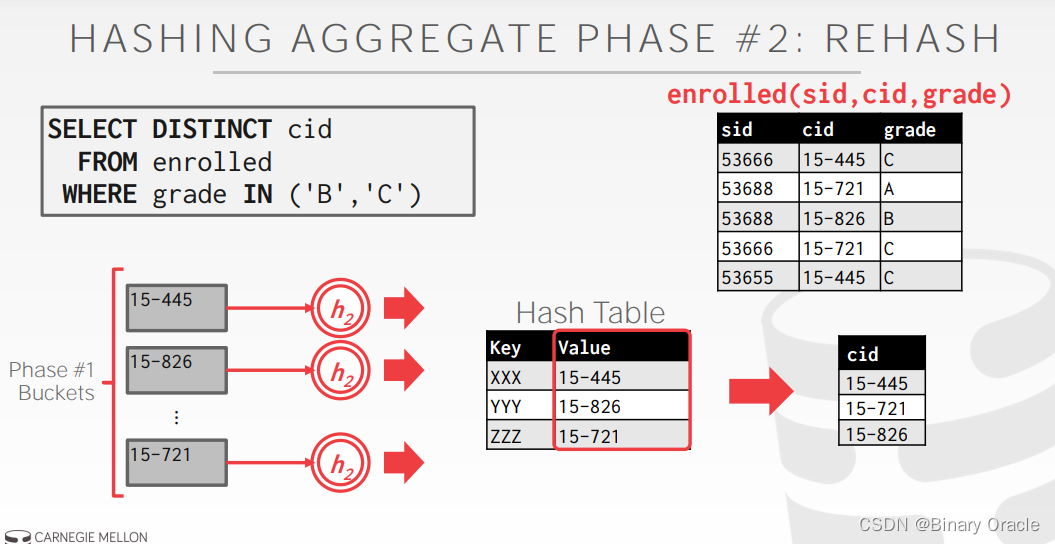
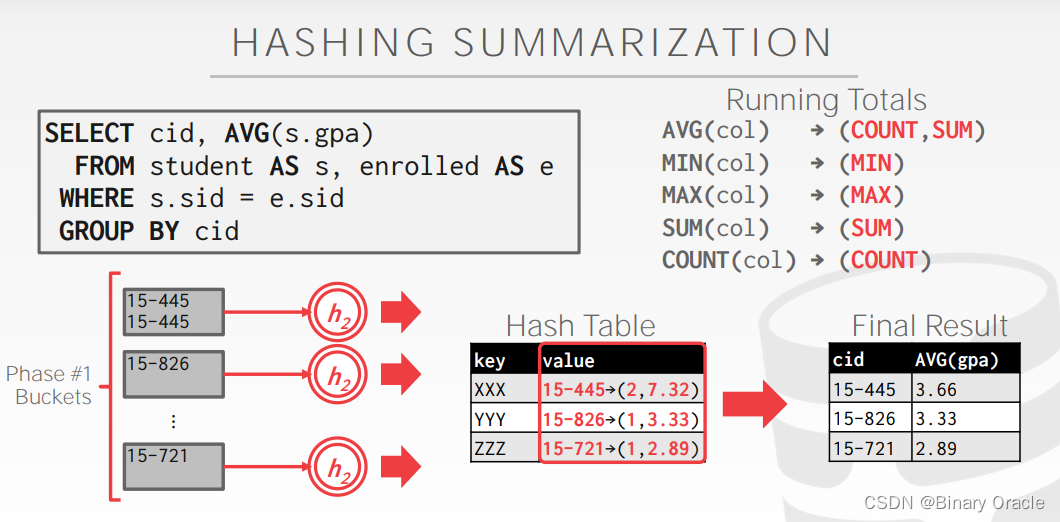
在 ReHash phase 中，存着 的键值对，当我们需要向 hash table 中插入新的 tuple 时：

• 如果我们发现相应的 GroupKey 已经在内存中，只需要更新 RunningVal 就可以
• 反之，则插入新的 GroupKey 到 RunningVal 的键值对

---

Cost Analysis

使用 hashing aggregation 可以聚合多大的 table ？假设有 B 个 buffer pages

• Phase #1：使用 1 个 page 读数据，B-1 个 page 写出 B-1 个 partition 的数据
• 每个 partition 的数据应当小于 B 个 pages

因此能够聚合的 table 最大为 B×(B−1)

• 通常一个大小为 N pages 的 table 需要大约根号N 个 buffer pages

---

小节

本节对应教材PDF