931. 下降路径最小和

题目描述：

给你一个 n x n 的方形整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

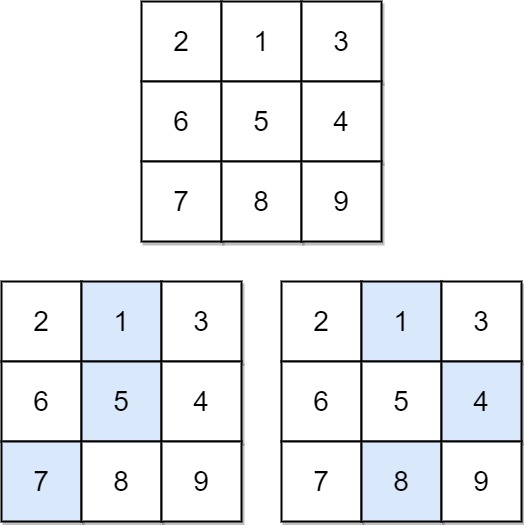
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

示例 2：

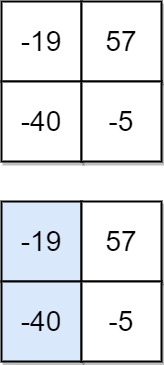
输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径

实现代码与解析：

动态规划

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) 
    {
        vector<vector<int>> f(matrix.size(), vector<int>(matrix.size(), 0));
        int n = matrix.size();
        for (int i = 0; i < n; i++) f[0][i] = matrix[0][i]; // 初始化
        for (int i = 1; i < n; i++)
        {
            for (int j = 0; j < n; j++)
            {
                if (j == 0) f[i][j] = min(f[i - 1][j], f[i - 1][j + 1]) + matrix[i][j]; // 上、右上
                else if (j == n - 1) f[i][j] = min(f[i - 1][j - 1], f[i - 1][j]) + matrix[i][j]; // 左上，上 
                else 
                {
                    //左上、上、右上
                    f[i][j] = min({f[i - 1][j - 1], f[i - 1][j], f[i - 1][j + 1]}) + matrix[i][j];
                }
            }
        }
        int res = 0x3f3f3f3f;
        for (int i = 0; i < n; i++)
        {
            res = min(res, f[n - 1][i]);
        }
        return res;
    }
};