LeetCode Java实现 222. 完全二叉树的节点个数

news2024/11/24 23:07:18

文章目录

- 题目
- 递归遍历左右子树个数实现
- - 思路
  - 具体代码实现
  - 缺点
- 根据完全二叉树性质优化
- - 思路
  - 具体代码实现
  - 优点
- 结语

题目

给你一棵完全二叉树的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

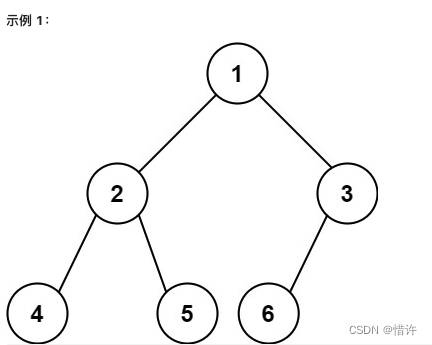
完全二叉树的节点个数

输入：root = [1,2,3,4,5,6]
输出：6

示例 2：
输入：root = []
输出：0

示例 3：
输入：root = [1]
输出：1

递归遍历左右子树个数实现

思路

采用递归分别获取左右子树结点数量+根结点个数1；

具体代码实现

  /**
     * 递归获取左右子树结点个数再加上根结点个数
     * @param node
     * @return
     */
    private static int getNodeNum(Node node) {
        if (node == null) {
            return 0;
        }
        return getNodeNum(node.left) + getNodeNum(node.right) + 1;
    }

缺点

时间复杂度为O(n)【每个结点都要遍历一次】；

根据完全二叉树性质优化

思路

根据完全二叉树性质可得如下结论：

如果左右子树高度相同，那其左子树一定是满二叉树，对应结点数量为2^h - 1，其中h表示左子树的高度
如果左右子树高度不相同，则其右子树一定是满二叉树，对应结点数量为2^h - 1，其中h表示右子树树的高度

因此，根据如上性质，我们可以对代码进行优化，如下：

具体代码实现

   private static int getNodeNum(Node root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        if (leftHeight == rightHeight) {
            //如果左子树高度等于右子树高度，说明左子树是满二叉树，需要1<<leftHeight 为 2^leftHeight 这里可以理解成算上了root结点
            return (1 << leftHeight) + getNodeNum(root.right);
        } else {
            //如果左右子树高度不相等，说明右子树是满二叉树
            return (1 << rightHeight) + getNodeNum(root.left);
        }
    }

    /**
     * 获取某个结点的高度
     *
     * @param node
     * @return
     */
    private static int getHeight(Node node) {
        int height = 0;
        while (node != null) {
            height++;
            node = node.left;
        }
        return height;
    }