一维DP数组的解法

背包最大重量为4。

物品重量和价值为：

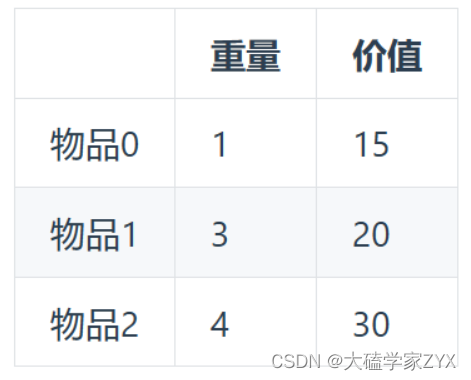
问背包能背的物品最大价值是多少？

在我们使用二维DP数组的时候，递推公式是dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]).

如果要降为一维DP数组，就是用dp[j]来表示递推。这里用j是为了j的含义和二维DP数组保持一致，下标含义都是背包的容量。

二维DP递推思路

原始的二维DP状态转移方程是：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])。

这个方程意味着，对于第i个物品和当前背包容量j，我们要么选择放入这个物品，要么不放。如果放入这个物品，就需要看在容量为j-weight[i]时，放入前i-1个物品的最大价值（也就是dp[i - 1][j - weight[i]] + value[i]），如果不放入这个物品，就是dp[i - 1][j]。然后取这两者之间的最大值。

二维背包DP数组情况示例如下图所示。

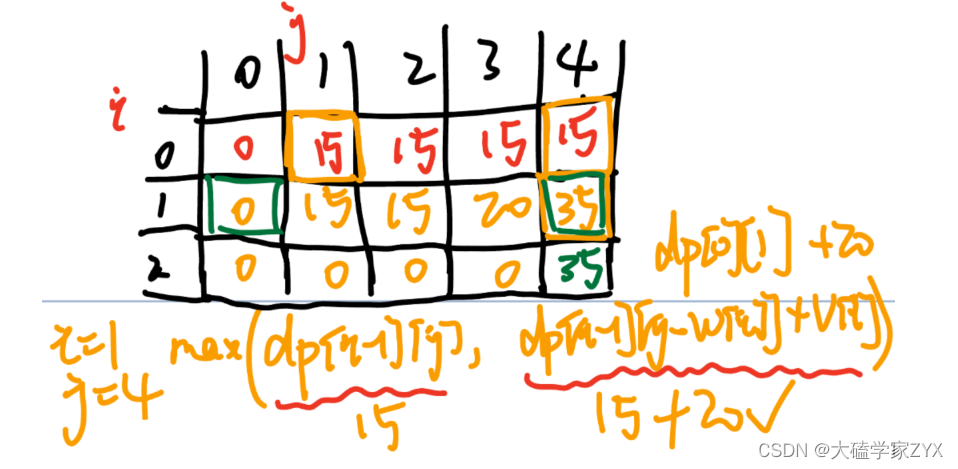
我们其实可以发现，如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);，与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。

滚动数组优化思路（重要）

leetcode题目343.整数拆分 里，其实有类似滚动数组的思想。整数拆分题目代码：

class Solution {
public:
    int integerBreak(int n) {
        //DP数组建立，注意数组本身容量赋值
        vector<int>dp(n+1,0);
        //初始化
        dp[2]=1;
        for(int i=3;i<=n;i++){
            for(int j=1;j<=i-1;j++){
                dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]));
            }
        }
        return dp[n];
    }
};

对于题目"整数拆分"来说，状态转移方程可以理解为：

dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]))

其中，dp[i]表示整数i能得到的最大乘积，j * (i - j)表示将i拆分为j和i-j两个数的乘积，j * dp[i - j]表示将i拆分为j和另一个数，另一个数可以继续拆分得到的最大乘积。

这里**dp[i]是通过遍历j来不断更新得到的，也就是说，dp[i]会在过程中不断地被自己更新，这种自我更新的思想就类似于滚动数组的思想**。

"滚动数组"是一种优化动态规划中空间复杂度的技术。它的主要思想是仅保留DP过程中需要的几个状态，而不是所有的状态，这样可以大大降低空间复杂度。

具体到背包问题，我们看到状态转移方程dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])，dp[i][j]仅仅依赖于上一层(i-1)的状态。这意味着在计算当前层状态时，我们实际上并不需要保留所有以前的状态，只需要保留上一层的状态即可。这就为使用滚动数组提供了可能。

那么，为何可以将dp[i - 1]这一层拷贝到dp[i]上，或者说使用一维数组代替二维数组？

我们可以将二维的dp数组理解为一个状态表格，其中行代表物品，列代表背包容量。如下图所示。

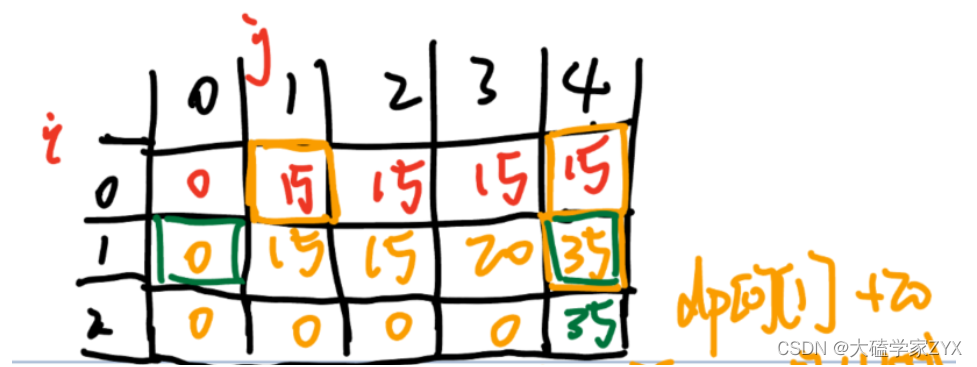
我们需要填满这个表格，每一个dp[i][j]都是由dp[i-1][j]或者dp[i-1][j-weight[i]]+value[i]转移过来的，也就是说**dp[i][j]只依赖于上一行(i-1)的状态。因此，我们实际上并不需要记住所有的行，只需要记住最后一行（也就是最新的一行）的状态就足够了**。

所以，我们将二维数组降维到一维数组，就是将dp[i][j]简化为dp[j]。在每一次迭代时，dp[j]在“滚动更新”：dp[j] = max(dp[j], dp[j - weight[i]] + value[i])，这个过程就像一个滚轮一样，不断地推进，并在这个过程中更新状态。因此，称之为"滚动数组"。

一维DP数组的含义

如果用一维数组优化这个问题，那么一维DP数组的含义是：dp[j]表示当前背包容量为j时的最大价值。

我们遍历所有的物品，对于当前的物品，如果我们选择放入，那么dp[j]就需要更新为dp[j - weight[i]] + value[i]，如果不放入，dp[j]就保持不变。然后我们取这两者之间的最大值，这样dp[j]就始终表示当前背包容量为j时的最大价值。

一维DP递推公式

一维DP的递推公式为：

dp[j]=max(dp[j],dp[j-weight[i]+value[i]]);//不放入i的情况，和放入i的情况

其中dp[j]表示容量为j时的最大价值，dp[j-weight[i]]+value[i]表示当放入特定物品i时的背包最大价值。递推公式遍历情况如下图所示：

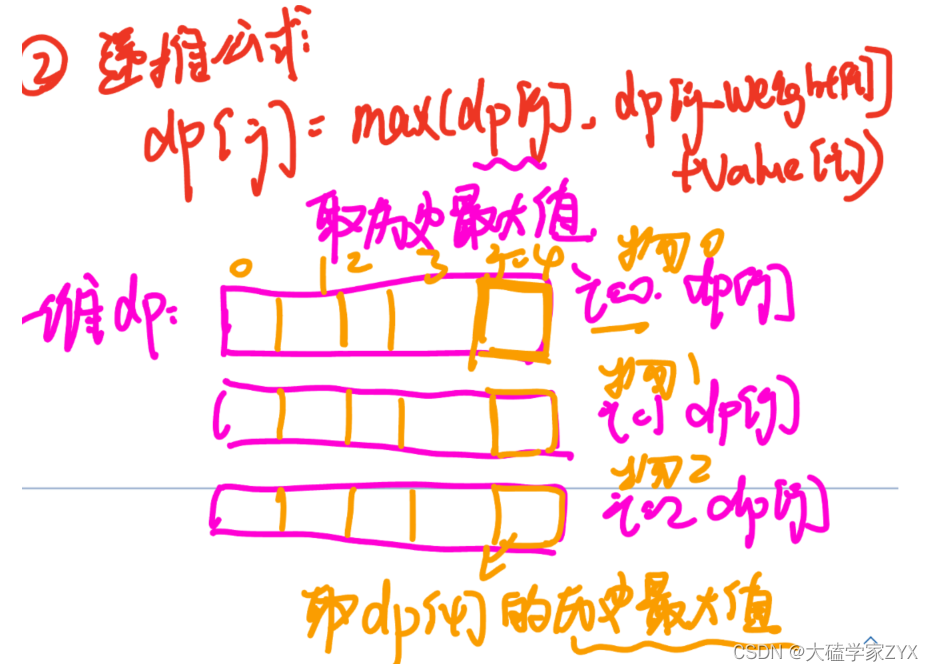
一维背包DP的递推思路就是，每遍历一个新的物品i，都从头遍历背包的所有容量j，得到每个i对应的dp[j]数组，并且不断更新历史最大值，确保dp[j]是容量为j时，背包的最大价值。（相当于压缩了二维DP数组中的i，只剩下了每个i对应的DP[j]，并且不断更新确保dp[j]最大。）

这就是滚动数组的思想：尽管我们在遍历的过程中，dp[j]的值会不断变化，但是每一次变化后，dp[j]都会保存当前为止遍历到的最大值。这样，在遍历完所有物品后，dp[j]就是我们的答案，即背包容量为j时的最大价值。这个过程中，dp[j]不断自我更新，就是滚动数组的关键所在。

一维DP的初始化

关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。

实际上一维背包问题直接全部初始化为0即可，因为不存在数组下标越界问题，且j<weight[i]的情况本来就是单独判断。

因为dp数组在推导的时要取价值最大的数，因此其余下标都初始化为0。

遍历顺序（重要）

一维背包问题的遍历顺序模板如下：

//最外层是物品，物品个数是weight.size()
for(i=0;i<weight.size();i++){
    //里层是背包容量，注意背包必须倒序遍历
    for(int j=bagWeight,j>=weight[i];j--){
        递推公式；
    }
}

这个遍历顺序需要注意两点：

• for的嵌套关系，最外层必须是物品，内层是背包，顺序不可颠倒；
• 内层for循环遍历背包的时候，需要倒着遍历，不能正序。

关于for内外嵌套和内层遍历顺序为什么不能改变的问题，在面试问题中进行了整理。

举例推导DP数组

一维DP，分别使用物品0，物品1和物品2来遍历背包所有容量，使得**dp[j]满足dp[j]是容量为j的最大价值**。

得到的DP数组结果如下：

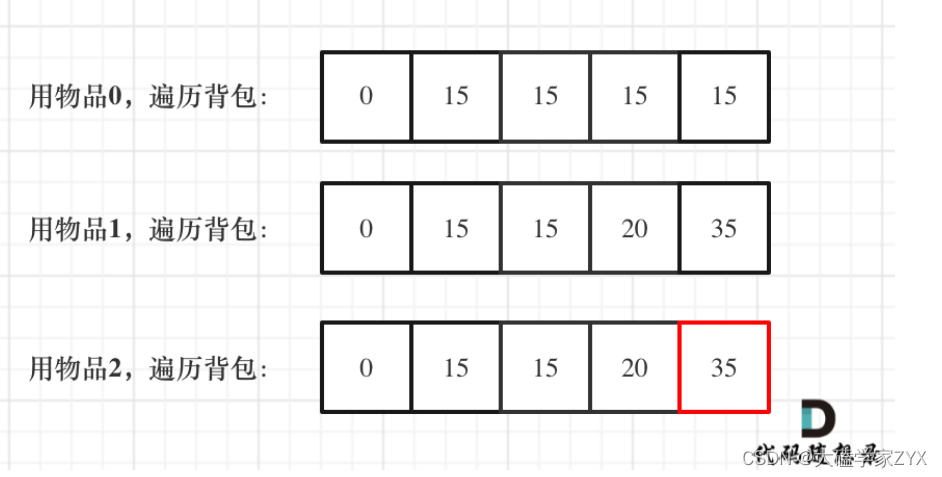
最后我们得到的结果，就是容量为4（背包最大容量就是4），且遍历完了最后一个物品的时候，dp[4]的数值。

结果在遍历完最后一个物品之后的原因是需要考虑所有备选的物品，这里需要结合dp[j]的含义进行理解。

一维DP数组完整版写法

• 题目描述：背包容量4，物品0{重量1,价值15}，物品1{重量3,价值20}，物品2{重量4,价值30}，求背包能装的最大价值
• 和前文二维DP数组的写法用了同一模板和样例，方便对比

#include <bits/stdc++.h>
using namespace std;


int knapsack(vector<int>& weight, vector<int>& value, int bagWeight) {
    int n=weight.size();//物品数量
    //初始化
    vector<int>dp(n+1,0);
    for(int i=0;i<n;i++){//遍历物品
        for(int j=bagWeight,j>weight[i];j--){//倒序遍历背包
            dp[j] = max(dp[j],dp[j-weight[i]]+value[i]);
        }
    }
    return dp[bagWeight];
}

void test_knapsack() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;

    cout << knapsack(weight, value, bagWeight) << endl;
}

int main() {
    test_knapsack();
}

一维DP的写法比二维DP写法简洁很多，且空间复杂度降了一个数量级。

因此遇到背包类问题，最好使用一维DP写法。

面试问题

面试有可能的情况，是要求先实现一个纯二维的01背包，如果写出来了，然后再问为什么两个for循环的嵌套顺序这么写？反过来写行不行？再讲一讲初始化的逻辑。

然后要求实现一个一维数组的01背包，最后再问，一维数组的01背包，两个for循环的顺序反过来写行不行？为什么？

为什么一维DP背包的for循环一定要倒序遍历

如果内层背包的for循环正序遍历的话，会出现物品被重复放置的情况。由于01背包每个物品只有一个，所以for循环必须倒序遍历，才能保证i的数值不变的情况下（也就是只有这一个物品的情况下），dp[j-weight[i]]不会被放进去很多次。

一旦正序遍历，例如i=0（物品0）的情况，物品0就会被放进去很多次！

例如下图所示的情况：

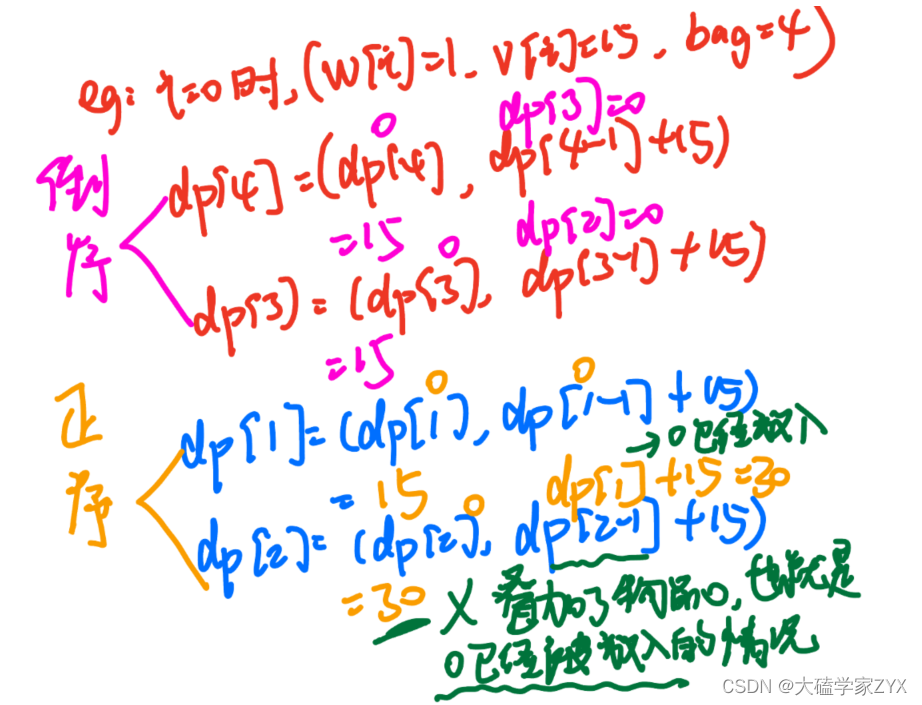
背包容量正序遍历的情况，对应的是完全背包的情况，在完全背包情况下，每个物品有无限个，因此物品自身的容量可以进行叠加。

而像上图的正序遍历情况，dp[2]的时候叠加了dp[1]的数值，而dp[1]的情况是放入了一个物品0。也就是说，dp[2]的情况是放入了两个物品0。不满足01背包问题每个物品只能有一个的要求。

为什么一维DP的for循环遍历，必须先遍历物品再遍历背包

从DP数组的含义来说：

物品的遍历顺序则必须在外层，这是因为我们需要对每一件物品进行处理，也就是每一件物品都需要有对应的DP[j]数组。dp[j]的含义是，考虑0–i所有物品情况下，背包的最大价值。因此每次处理一件新的物品时，我们都需要用到前面物品的信息（即dp数组），也就是说必须在处理新的物品前，就已经处理完前面的所有物品。因此，我们需要在外层循环中遍历物品。

如果将这两层循环的顺序进行调换，那么处理背包容量为j的情况时，很可能还没有处理完所有的物品，因此**dp[j]中存储的并不是在考虑了所有前面的物品后，背包容量为j时能取得的最大价值**，这与DP数组的含义不符合。

从背包放入物品的角度来说：

因为一维dp的写法，背包容量一定是要倒序遍历（原因在上面）。而如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。

倒序遍历的原因是，本质上还是一个对二维数组的遍历，并且右下角的值依赖上一层左上角的值，因此需要保证左边的值仍然是上一层的，从右向左覆盖。

我们还是以背包容量为4，物品有0 1 2三个并且分别有不同的value和weight的例子来举例。

一维DP背包问题是遍历所有的物品i，每个i都更新dp[j]的数组，使得dp[j]的值是容量为j且考虑0-i所有物品在内的最大价值。

例如下图所示，是物品在外的情况下dp[j]数组的例子。可以看出，遍历到i=1的时刻，dp[j]数组已经继承了i=0的所有状态。

但是，如果物品在内层for循环，背包容量在最外层，dp[j]的情况如下图所示：

（背包里只放入了一个物品）

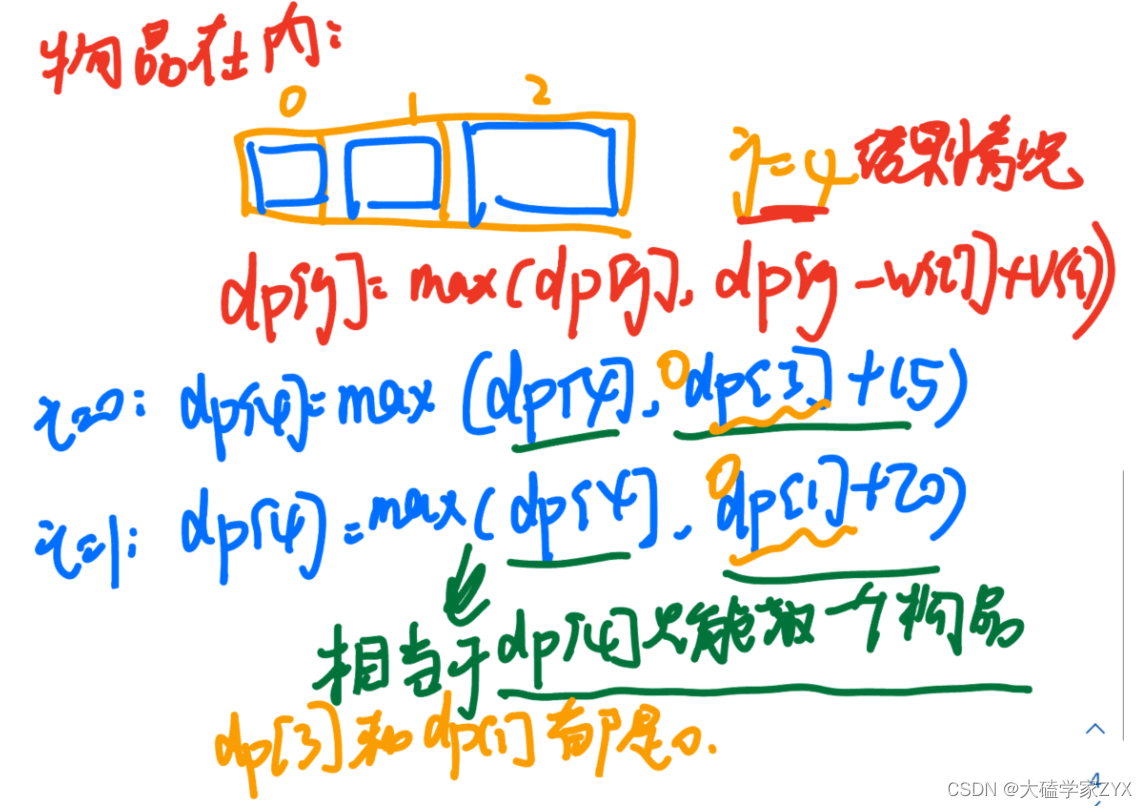
从这个例子中我们可以看到，每次处理一件新的物品时，都需要用到前面物品的信息。只有当我们已经处理完所有的前面的物品，以及背包容量较大的情况，我们才能正确地处理当前的物品和背包容量。因此物品的for循环必须在外层，而背包容量的for循环必须在内层，且背包必须从大到小进行遍历。