一、二分

1、二分易错点

1、循环变量

while(left < right) 还是while(left <=right)

2、判断条件

if(num[mid] > tar) mid = right 还是 mid = right -1

2、循环不变量

[left, right]
[left, right)
(left, right]

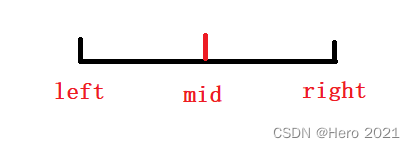
3、左闭右闭写法

当时左闭右闭时，while循环里面的条件，我们可以先假设，有等号即有left=right的情况，例如[1,1]这个区间，那么循环是要进入里面的，所以要取得等号。

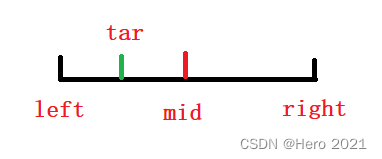
判断的时候，nums[mid]>tar，那么必然tar不在右半区间，所以right=mid-1

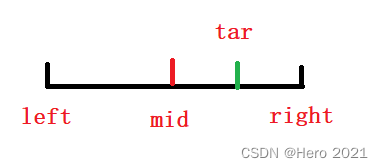
nums[mid]<tar，那么必然tar不在左半区间，所以left=mid+1

## 模板
left=0
right=size-1
while(left<=right)
{
	int mid=(left+right)/2;
	if(nums[mid]>tar)
	{
		right=mid-1;
	}
	else if(nums[mid]<tar)
	{
		left=mid+1;
	}
	else
	{
		return mid;
	}
}
return -1;

4、左闭右开写法

例如[1,1)，既包含1又不包含1，这是个合法的区间吗？所以while(left < right)即可。

判断的时候，因为nums[mid]>tar，所以下一次搜索的时候，区间中mid必然不会在这个左半区间，所以right=mid。
当nums[mid]<tar，因为是左闭右开，明确了tar是大于nums[mid]的，那么下一次搜索的区间的左边界必然是left=mid+1。

right的取值也要注意，因为咱的区间是不包含右边界的，但是还是要包含所有的数字，right相当于变大了1，所以right=size

## 模板
left=0
right=size
while(left<=right)
{
	int mid=(left+right)/2;
	if(nums[mid]>tar)
	{
		right=mid;
	}
	else if(nums[mid]<tar)
	{
		left=mid+1;
	}
	else
	{
		return mid;
	}
}
return -1;

二、题

704.二分查找

class Solution
{
public:
    int search(vector<int> &nums, int tar)
    {
        // 左闭右开
        int left = 0;
        int right = nums.size();
        while (left < right)
        {
            int mid = left + (right - left) / 2;
            if (nums[mid] > tar)
                right = mid;
            else if (nums[mid] < tar)
                left = mid + 1;
            else
                return mid;
        }
        return -1;
    }
};

27.移除元素

删除元素并不是删除，而是覆盖，erase这个操作是O(N)的时间复杂度。
暴力法：O(N²) 的时间复杂度，两层for循环。

// 暴力  n^2 超时了
class Solution
{
public:
    int removeElement(vector<int> &nums, int val)
    {
        int size = nums.size();
        for (int i = 0; i < nums.size(); i++)
        {
            if (nums[i] == val)
            {
                // 将整个剩余的数组，整体移动一位
                for (int j = i + 1; j < nums.size(); j++)
                {
                    nums[j - 1] = nums[j];// 从j -1 开始为了防止越界
                }
                i--;
                size--;
            }
        }
        return size;
    }
};

双指针解法：O(N)
fast快指针：用来获取新数组中的元素，新数组就是不含有目标元素的数组
slow慢指针：用来获取新数组中需要更新的位置

class Solution
{
public:
    int removeElement(vector<int> &nums, int val)
    {
        int fast = 0;
        int slow = 0;
        for (fast = 0; fast < nums.size(); fast++)
        {
        	// 不是我们需要找寻的元素，就更新原数组
            if (nums[fast] != val)
            {
                nums[slow] = nums[fast];
                slow++;
            }
            // 找到 nums[fast]==val 我们就不执行更新操作，而是直接变成fast++
        }
        return slow;
    }
};