一、LeetCode503. 下一个更大元素 II
1:题目描述(503. 下一个更大元素 II)
给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1 。

2:解题思路
class Solution:
def nextGreaterElements(self, nums: List[int]) -> List[int]:
# # 用两个nums数组,拼成一个nums_pin,然后再使用单调栈
# result = [-1] * (2*len(nums))
# res_stack = [0]
# nums_pin = nums[:]
# for item in nums:
# nums_pin.append(item)
# for i in range(1, len(nums_pin)):
# if nums_pin[i] <= nums_pin[res_stack[-1]]:
# res_stack.append(i)
# else:
# while len(res_stack)!=0 and nums_pin[i] > nums_pin[res_stack[-1]]:
# index = res_stack.pop()
# result[index] = nums_pin[i]
# res_stack.append(i)
# return result[:len(nums)]
# 循环遍历nums
result = [-1]*len(nums)
res_stack =[0]
for i in range(1, 2*len(nums)): # 遍历长度为两个nums
# 当前遍历的值i,除以nums的长度取余,就可以得到当前i对应在nums中的下标
if nums[i%len(nums)] <= nums[res_stack[-1]]:
res_stack.append(i%len(nums))
else:
while len(res_stack)!=0 and nums[i%len(nums)] > nums[res_stack[-1]]:
index = res_stack.pop()
result[index] = nums[i%len(nums)]
res_stack.append(i%len(nums))
return result二、LeetCode42. 接雨水
1:题目描述(42. 接雨水)
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
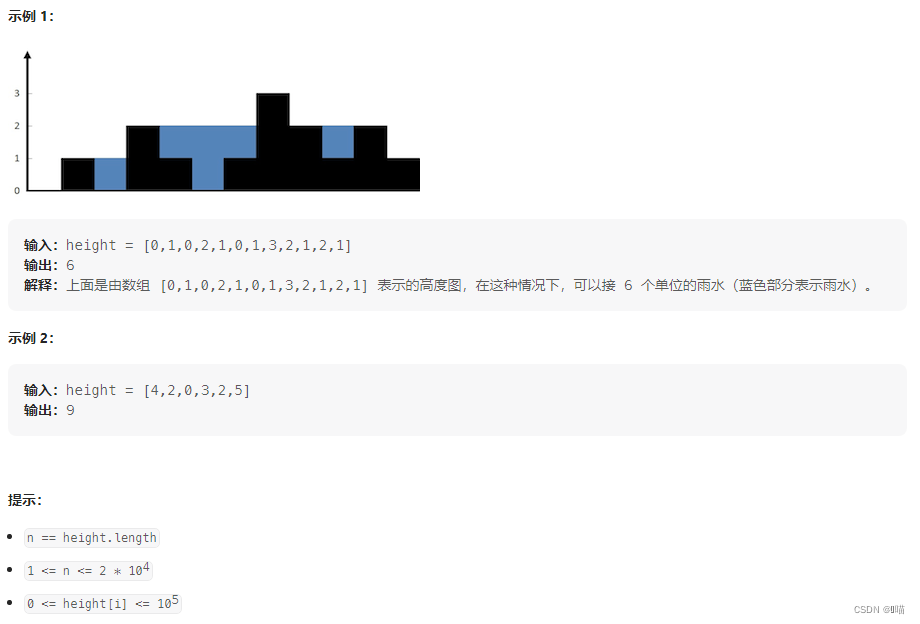
2:解题思路
解法一:双指针
class Solution:
def trap(self, height: List[int]) -> int:
# 按照列来计算雨水的高度,雨水的宽度均为1,求出每列雨水的体积,然后求和
# 双指针
# 遍历数组height,求每列柱子的左侧最高高度left_height,右侧最高高度right_height,
# 取两侧高度最小值 减去 柱子本身的高度,就是水滴的高度,min(left_height, right_height)-height[i]
height_sum = 0
for i in range(len(height)):
# 第一个柱子和最后一个柱子不接水
if i == 0 or i == len(height)-1:
continue
# 记录右边柱子的最高高度
right_height = height[i]
# 记录左边柱子的最高高度
left_height = height[i]
# 从当前遍历的下一个位置,开始遍历剩下的height,求当前遍历位置右边的最高高度
for r in range(i+1, len(height)):
if height[r] > right_height:
right_height = height[r]
# 从当前遍历的上一个位置,开始遍历前面的height,求当前遍历位置左边的最高高度
for l in range(i-1, -1, -1):
if height[l] > left_height:
left_height = height[l]
# 求当前位置能接水的高度,左右高度的最小高度 减去 当前位置本身的高度,
h = min(left_height, right_height) - height[i]
if h > 0:
height_sum += h
return height_sum解法二:动态规划
class Solution:
def trap(self, height: List[int]) -> int:
# 动态规划
if len(height) <= 2:
return 0
res = 0
maxleft = [0]*len(height)
maxright = [0]*len(height)
# 记录每个柱子左边柱子的最大高度
maxleft[0] = height[0]
for l in range(1, len(height)):
# 在前一个柱子左边的最大高度,和当前柱子的高度中取最大值
maxleft[l] = max(maxleft[l-1], height[l])
# 记录每个柱子右边柱子的最大高度,从后往前遍历
maxright[len(height)-1] = height[len(height)-1]
for r in range(len(height)-2, -1, -1):
# 在后一个柱子右边的最大高度,和当前柱子的高度中取最大值
maxright[r] = max(maxright[r+1], height[r])
# 求和
for i in range(len(height)):
h = min(maxleft[i], maxright[i]) - height[i]
if h > 0:
res += h
return res解法三:单调栈
class Solution:
def trap(self, height: List[int]) -> int:
# 单调栈
# 按照行的方向来计算雨水
# 从栈顶到栈底的顺序,从小到大
# 通过三个元素来接水:栈顶、栈顶的下一个元素,以及即将入栈的元素
# 雨水的高度是:min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度
# 即:min(栈顶下一个元素,即将入栈的元素) - 栈顶的元素
# 雨水的宽度是:凹槽右边的下标-凹槽左边的下标-1(只求中间宽度)
res = 0
res_stack = [0]
for i in range(1, len(height)):
# 情况一:即将入栈的元素小于栈顶元素,直接入栈
if height[i] < height[res_stack[-1]]:
res_stack.append(i)
# 情况二:即将入栈的元素小于栈顶元素,将栈顶元素弹出,入栈即将入栈的元素
# 因为,当前柱子高度和栈顶一致时,左边的一个是不可能存在雨水的,所以保留右侧新柱子
# 需要使用最右边的柱子来计算
elif height[i] == height[res_stack[-1]]:
res_stack.pop()
res_stack.append(i)
# 情况三:即将入栈的元素大于栈顶元素,出现凹槽了
else:
# 抛出所有较低的柱子
while res_stack and height[i] > height[res_stack[-1]]:
# 栈顶就是中间的柱子,就是凹槽底部的高度
mid_height = height[res_stack[-1]]
# 弹出栈顶元素
res_stack.pop()
if res_stack:
right_height = height[i]
left_height = height[res_stack[-1]]
# 两侧的最小高度 - 凹槽底部的高度
h = min(right_height, left_height) - mid_height
# 两侧柱子的中间宽度:右侧柱子的下标 - 左侧柱子的下标 - 1
w = i - res_stack[-1] -1
# 求体积
res += h*w
# 栈为空,将当前元素入栈
res_stack.append(i)
return res















![[附源码]Python计算机毕业设计SSM基于推荐算法的汽车租赁系统(程序+LW)](https://img-blog.csdnimg.cn/e1c2e6a5327248c4b919a4694816a836.png)