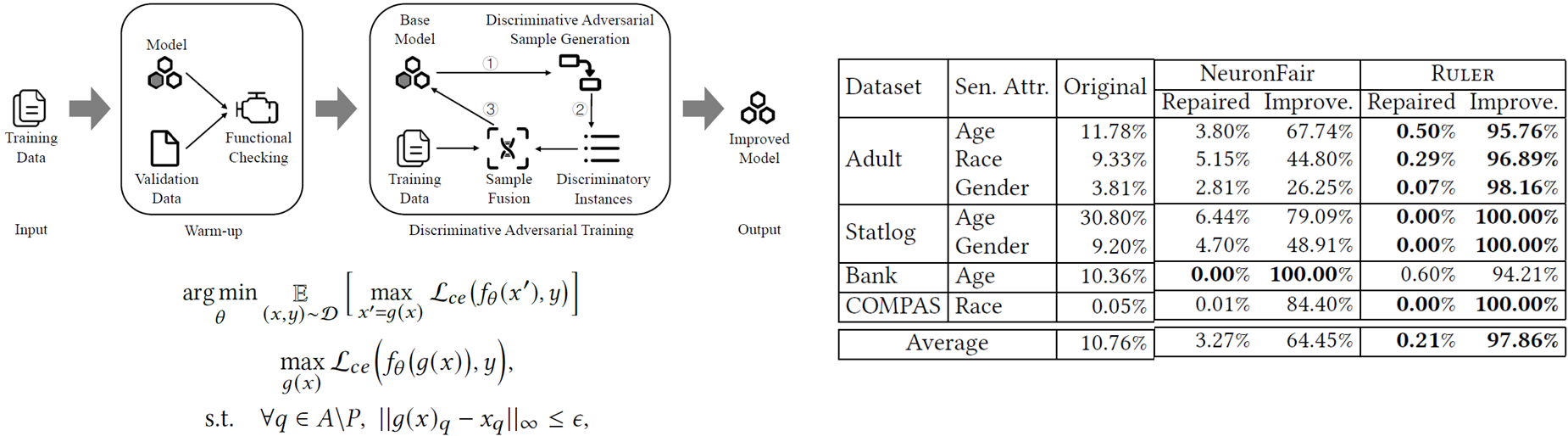
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
matlab学习笔记(八)
- 一、傅里叶变换的MATLAB求解
- 二、连续时间信号的频谱图
- 三、MATLAB分析LTI系统的频率特性
一、傅里叶变换的MATLAB求解
MATLAB的symbolic Math Toolbox 提供了直接求解傅里叶变换及逆变换的函数fourier()及ifourier()两者的调用格式如下。
Fourier 变换的调用格式F=fourier(f): 默认返回是关于w的函数。
F=fourier(f,v):它返回函数F是关于符号对象v的函数
傅里叶的逆变换 f=ifourier(F):
案例1:

syms t w
Fw=fourier(exp(-2*abs(t)))
运行结果:
Fw =
4/(w^2 + 4)
案例二:
>> syms t w
>> ft=ifourier(1/(1+w^2),t)
运行结果:
ft =
(pi*exp(-t)*heaviside(t) + pi*heaviside(-t)*exp(t))/(2*pi)
二、连续时间信号的频谱图
用MATLAB符号算法求傅里叶变换有一定局限,当信号不能用解析式表达时,会提示出错,这时用MATLAB的数值计算也可以求连续信号的傅里叶变换,计算原理是
当 足够小时,近似计算可满足要求。若信号是时限的,或当时间大于某个给定值时,信号已衰减的很厉害,可以近似地看成时限信号时,n的取值就是有限的,设为N,有
时间信号取样间隔 应小于奈奎斯特取样时间间隔,若不是带限信号可根据计算精度要求确定一个频率 W0为信号的带宽。
案例一:
syms t;
ft=sym(4*cos(2*pi*6*t)*(heaviside(t+1/4)-heaviside(t-1/4))')
Fw=simplify(fourier(ft))
subplot(121)
ezplot(ft,[-0.5 0.5]),grid on
subplot(122)
ezplot(abs(Fw),[-24*pi 24*pi]),grid on
运行结果:

案例二:运行如下命令,计算0~2pi频率范围内以间隔0.5取样的系统频率响应的样值
a=[1 2 1];
b=[0 1];
h=freqs(b,a,0:0.5:2*pi)
运行结果:
h =
Columns 1 through 4
1.0000 0.4800 - 0.6400i 0 - 0.5000i -0.1183 - 0.2840i
Columns 5 through 8
-0.1200 - 0.1600i -0.0999 - 0.0951i -0.0800 - 0.0600i -0.0641 - 0.0399i
Columns 9 through 12
-0.0519 - 0.0277i -0.0426 - 0.0199i -0.0355 - 0.0148i -0.0300 - 0.0113i
Column 13
-0.0256 - 0.0088i
案例二:求信号f(t)=u(t+1)-u(t-1) 的傅里叶变换
R=0.02;t=-2:R:2;
f=heaviside(t+1)-heaviside(t-1);
W1=2*pi*5;
N=500;k=0:N;W=k*W1/N;
F=f*exp(-j*t'*W)*R;
F=real(F);
W=[-fliplr(F),F(2:501)];
F=[fliplr(F),F(2:501)];
subplot(2,1,1);plot(t,f);
xlabel('t');ylabel('f(t)');
title('f(t)=u(t+1)-u(t-1)');
subplot(2,1,2);plot(W,F);
xlabel('w');ylabel('F(w)');
运行结果:

三、MATLAB分析LTI系统的频率特性
当系统的频率响应H(jw)是jw的有理多项式时,有

h:频率响应
w:角频率,0~π
freqs函数可直接计算系统的频率响应的数值解。其调用格式如下
H=freqs(b,a,w)
其中,a和b分别是H(jw)的分母和分子多项式的系数向量,w为形如w1:p:w2的向量,定义系统频率响应的频率范围,w1为频率起始值,w2为频率终止值,p为频率取样间隔。H返回w所定义的频率点上,系统频率响应的样值。
案例一:

w=0:0.025:5;
b=[1];a=[1,2,2,1];
H=freqs(b,a,w);
subplot(2,1,1);
plot(w,abs(H));grid;
xlabel('\omegq(rad/s)');
ylabel('|H(j|omega)|');
title('H(jw)的频幅特性');
subplot(2,1,2);
plot(w,angle(H));grid;
xlabel('\omega(rad/s)');
ylabel('pui(|omega)');
title('H(jw)的相频特性');
运行结果:

案例二:
w=0:0.025:5;
b=[1];a=[4/50,2/5,1];
H=freqs(b,a,w);
subplot(2,1,1);
plot(w,abs(H));grid;
xlabel('\omegq(rad/s)');
ylabel('|H(j|omega)|');
title('H(jw)的频幅特性');
subplot(2,1,2);
plot(w,angle(H));grid;
xlabel('\omega(rad/s)');
ylabel('pui(|omega)');
title('H(jw)的相频特性');
运行结果:















![[附源码]Python计算机毕业设计SSM基于推荐算法的汽车租赁系统(程序+LW)](https://img-blog.csdnimg.cn/e1c2e6a5327248c4b919a4694816a836.png)