👑作者主页:@进击的安度因
🏠学习社区:进击的安度因(个人社区)
📖专栏链接:有营养的算法笔记
文章目录
- 一、铺垫
- 二、整数二分模板分析
- 三、模板应用 —— 数的范围
- 四、浮点二分模板分析
- 五、模板应用 —— 数的三次方根
二分算法有时是一个很玄乎的算法,有时稀里糊涂就对了,有时不是死循环就是查找错误。其实就是边界问题处理不当,所以对于二分来说,很有必要有一定的模板,帮助我们快速解决问题。
今天,我们将围绕整数二分和浮点二分进行讲解。
一、铺垫
概念:二分算法,就是在一段 单调且有序 的区间中通过某些条件,不断对二分的起始边界和结束边界进行调整。从而让区间不断压缩,直至找出二分答案,在每次二分后,区间或多或少都会改变。
二分对于我们来说应该是不陌生的。二分查找 大家应该都听说过,这其实就是二分的一层演变拓展,变为更加精确的查找某些值。
概念部分对 单调性 略有提及。其实对于二分算法,区间具有单调性一定可以二分,但是二分的题目不一定有单调性。
对于二分算法来说,二分是一定会找到答案的。因为二分不断压缩区间,最后必定会分出一个值。
但是这个答案仅仅是对于二分这个算法求出的答案。答案是否正确,还是要结合题目判断。简约的说就是二分的答案不一定是题目的答案,但是二分一定会有答案,无解是对于问题的。
有了这些 铺垫 ,我们再看板子。
二、整数二分模板分析
整数二分有两个板子,这也是我觉得最好的板子,简洁,清晰明了。
我们的两个板子二分的最终结果为 边界值 。
模板1:区间 [l, r] 被划分成 [l, mid] 和 [mid + 1, r] 时使用
bool check(double x) {/* ... */} // 检查x是否满足某种性质
int binarySearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
模板2:区间 [l, r] 被划分成 [l, mid - 1] 和 [mid, r] 时使用
int binarySearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
这里的 check(mid) 函数是为了判断每次二分取的 中间点 mid 是否满足特定性质,从而对区间进行 正确压缩 。
接下来,我们对两个板子进行分析:
模板1:
假定一段区间单调递增,区间最左端为 l,区间最右端为 r,区间中点:mid = (l + r) / 2

对于 模板 1 ,二分找的是 蓝色区间的左边界点 。
mid 可能出现在两个区间中。 check(mid) 检查 mid 是否在 蓝色区间 中。
mid所在区间为 蓝色区间 :
此时 check(mid) 为 真 ,答案在 [l, mid] 区间内。这里取 mid 的原因是查找的是蓝色左端点,mid 在蓝色区间,mid 可能就 是答案 。由于查找的是 左端点 ,所以其他 大于 mid 的情况就 不可能 了。调整 r = mid,缩短右边,在左边找答案。
mid所在区间为 红色区间 :
此时 check(mid) 为 假 ,答案在 [mid + 1, r] 区间内。这里不取 mid 的原因是查找的是蓝色左端点,mid 在红色区间,所以答案肯定不会落在 mid 上,只有 mid + 1 才 有可能 。调整 l = mid + 1,缩短左边,在右边找答案。
区间划分情况为 [l, mid] 和 [mid + 1, r]。
模板 2:
假定一段区间单调递增,区间最左端为 l,区间最右端为 r,区间中点:mid = (l + r + 1) / 2(这里为什么这么取中点我们先不关心,马上会讲解)

对于 模板 2,二分找的是 红色区间的右边界点。
mid 可能出现在两个区间中。check(mid) 检查 mid 是否在 红色区间 中。
mid所在区间为 红色区间 :
此时 check(mid) 为 真 ,答案在 [mid, r] 区间内。mid 在红色区间中,答案 可能取到 mid ,所以区间包含 mid。由于查找的是 右端点,所以小于 mid 的无需考虑。调整 l = mid,缩短左边,在右边查找答案 。
mid所在区间 蓝色区间 :
此时 check(mid) 为 假 ,答案在 [l, mid - 1] 区间内。mid 在蓝色区间中,答案不可能取到 mid,所以区间不包含 mid ,只有 mid - 1 才 有可能 。右边的区间都不需要考虑了。调整 r = mid - 1,缩短右边,在左边查找答案 。
区间划分情况为 [l, mid - 1] 和 [mid, r] 。
讲到这,我们对二分的情况有一些了解后,我们解答一下,为什么 模板 2 的 mid = (l + r + 1) / 2 :
/ 是下取整的,如果 l = r - 1 ,二分取中点 mid 时,mid = (l + r) / 2 = (l + l + 1) / 2 = l
一旦 check(mid) 满足,那么 l = mid,由于 mid = l,那么 l 就被调整为了 l ,相当于没变,这就 死循环 了。+1 就可以避免掉这种情况。
总结一下 :模板 1 找 区间左边界点,模板 2 找 区间右边界点。

例如模板1在上图中找的就是 第一个 3,左端点 ;模板2找的是 最后一个3,右端点 。
三、模板应用 —— 数的范围
描述:
给定一个按照升序排列的长度为 n 的整数数组,以及 q 个查询。
对于每个查询,返回一个元素 k 的起始位置和终止位置(位置从 0 开始计数)。
如果数组中不存在该元素,则返回 -1 -1。
输入格式:
第一行包含整数 n 和 q,表示数组长度和询问个数。
第二行包含 n 个整数(均在 1 ∼ 10000 范围内),表示完整数组。
接下来 q 行,每行包含一个整数 k,表示一个询问元素。
输出格式:
共 q 行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回 -1 -1。
数据范围:
1 ≤ n ≤ 100000
1 ≤ q ≤ 10000
1 ≤ k ≤ 10000
输入样例:
6 3
1 2 2 3 3 4
3
4
5
输出样例:
3 4
5 5
-1 -1
思路:
这道题就是模板的经典应用,例如查找的是这样一段区间:

我们查找的是 3 出现的范围,那么返回的就是 3 出现位置的 左端点 和 右端点 。
这就很简单了,左端点就套用模板1,右端点套用模板2。
需要注意的就是 二分结果是否正确 的判断,以及 check(mid) 的写法。
并且二分结束时,l 是必定等于 r的,所以到时候输出 l 和 r 任意一个即可。
小技巧:如果拿捏不准该使用哪个模板,那么就现根据题意写出
check后的区间调整状况,根据这个选择模板。
让我们看看代码怎么写:
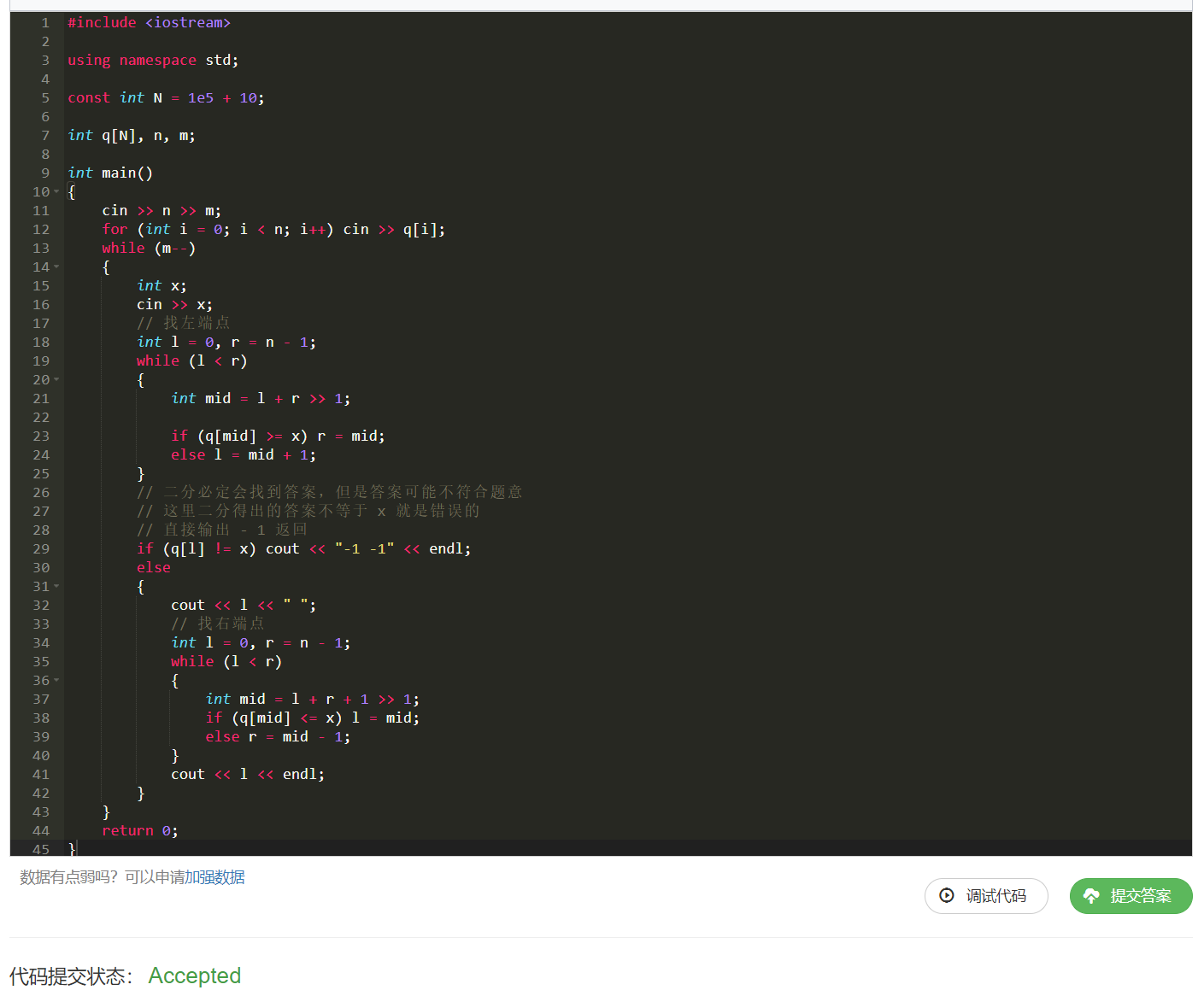
AC,没问题
四、浮点二分模板分析
相较于整数二分,浮点二分更加简单:
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double binarySearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}
浮点二分 不需要 考虑 向上取整 或 向下取整 。
对于浮点二分来说,调整区间的时候甚至不需要 +1 或 -1。因为是浮点数,+1, -1就可能会错过答案,所以让其等于 mid 自行调整即可。
接下来写道浮点二分题目来练练手。
五、模板应用 —— 数的三次方根
描述:
给定一个浮点数 n ,求它的三次方根。
输入格式:
共一行,包含一个浮点数 n 。
输出格式:
共一行,包含一个浮点数,表示问题的解。
注意,结果保留 6 位小数。
数据范围:
−10000 ≤ n ≤ 10000
输入样例:
1000.00
输出样例:
10.000000
思路:
数据范围为 [-10000, 10000],所以左右边界 l 和 r 就给定这个范围。
另外需要考虑一下精度问题,题目要求保留 6 位小数,一般我们总结的规律是这样的:精度总是比输出位数多2位,输出6位小数,那么精度就给8位小数。
这里取中的话 (l + r) / 2必须写成 / 的形式,因为是浮点数,无法使用 >> 操作符,不要用错了。
然后再考虑一下 check 函数写法:
- 如果
mid^3 >= x,说明答案肯定不在右半区间,到左半区间[l, mid]找,r = mid - 如果
mid^3 < x,说明答案肯定不在左半区间,到右半区间[mid, r]找,l = mid
同理,check 函数也可以写成 mid^3 <= x ,处理情况相似,自己推一下就明白了。
让我们看看代码怎么写:
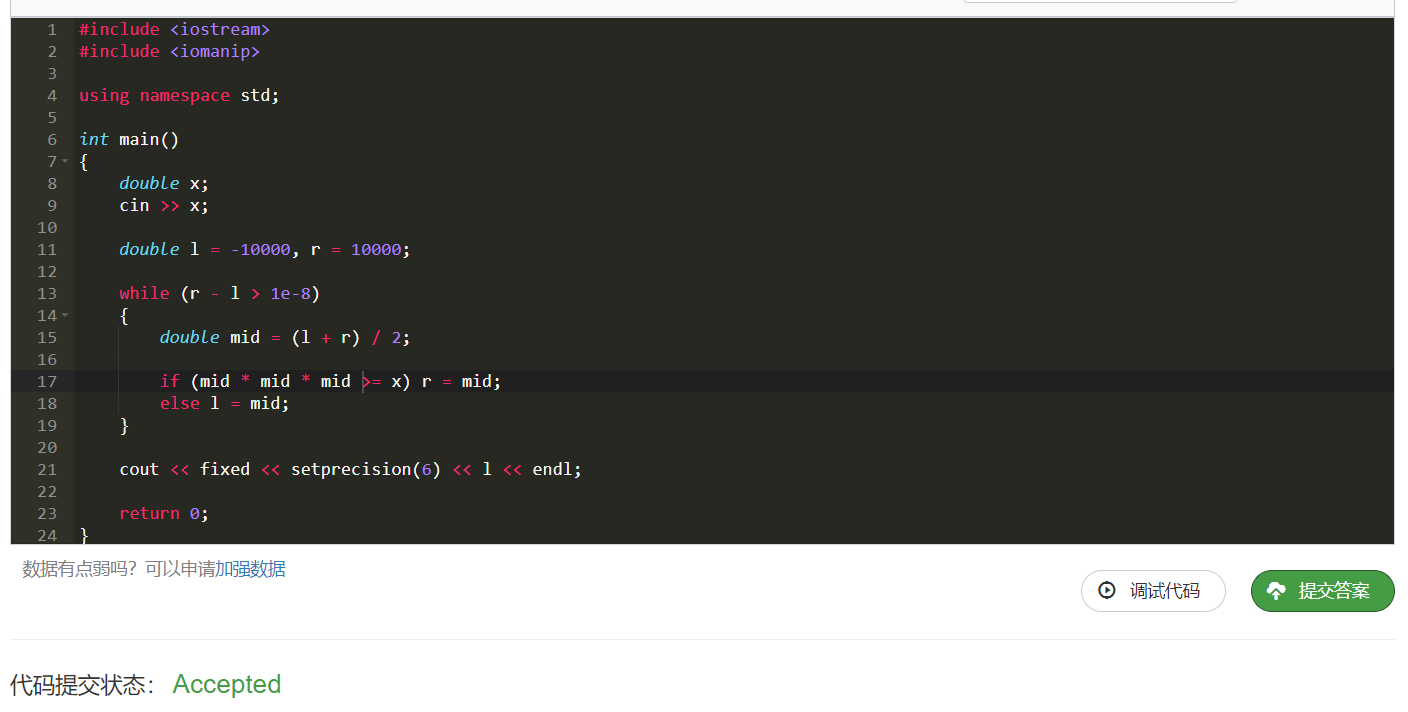
AC,没问题
到这里,本篇博客就到此结束了。一般情况下,二分的题型是都可以使用今天模板解答的。
所以看懂看明白就很重要,一定要多画图推导和多写。
如果觉得anduin写的还不错的话,还请一键三连!如有错误,还请指正!
我是anduin,一名C语言初学者,我们下期见!


![[附源码]JAVA毕业设计翔隆生鲜超市进货管理系统(系统+LW)](https://img-blog.csdnimg.cn/2a112239172e4c31b023ff003f8d29fd.png)