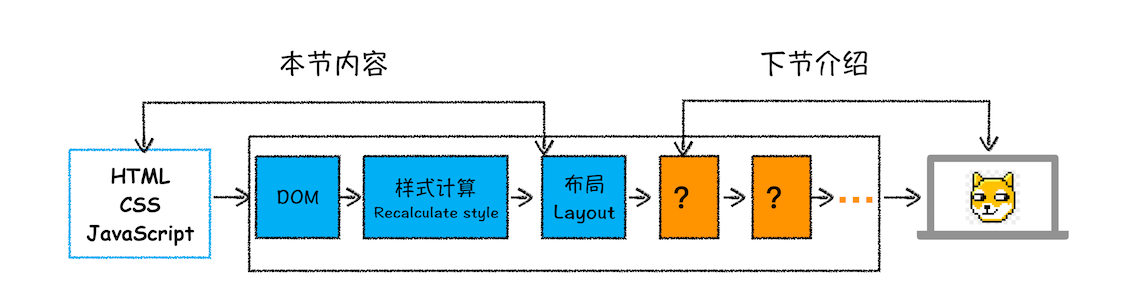
三维重建以及神经渲染中的学习
公众号AI知识物语
本文内容为参加过去一次暑期课程学习时的笔记,浅浅记录下。
显示表征:
点云points:由一组离散三维点表征物体表面
+推理速度快,容易获取
-离散表征,无拓扑关系

[Fan et al,CVPR 2017]
网格(Meshes):
由离散点和面表征物体表面
+推理速度快,具备拓扑关系
-离散表征,拓扑关系难优化

[Groueix et al,CVPR 2018]
栅格(Voxels):
整个场景表征为离散化
+推理速度快,可表征拓扑关系
-栅格分辨率受限,可视化的时候要转化为显示表征

[Maturana et al IROS 2015]
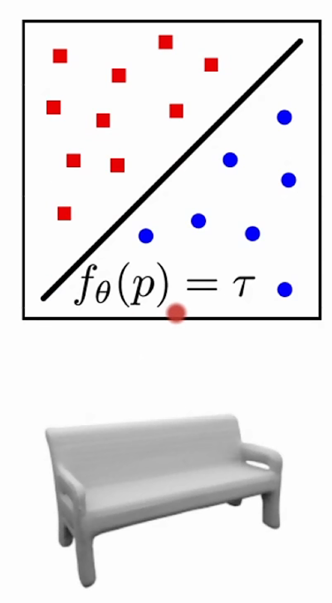
神经隐式表征(Neural Implicit Representation)
+可表征拓扑关系,不受分辨率限制
-推理速度慢,可视化的时候要转为显示表征
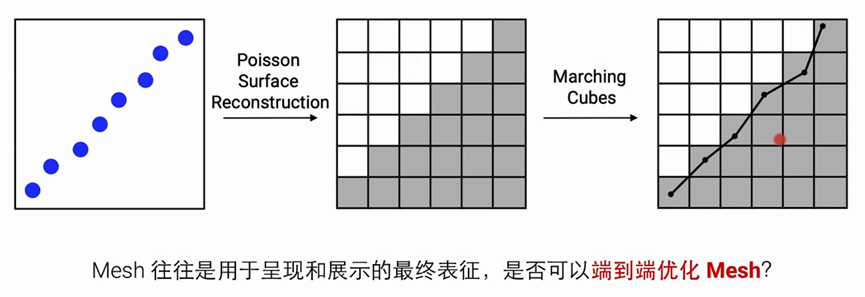
在三维重建的过程中,不管是否以点云开始,最终我们都想用Mesh网格来呈现其最终表征
那是否可以端到端来优化Mesh?
什么是端到端学习参考:https://www.zhihu.com/question/349900338
接下来一个工作:
如何优化隐式表征,把 marching Cubes变成可导,这样我就可以去优化任意拓扑结构的一个mesh
第二个工作是:
如何优化点云,把pine变成可导,最终还是可以服务于端到端的优化最终的mesh
Marching Cubes是一种用于三维体数据的表面重建算法。它将体数据分割成小的立方体单元,然后根据每个单元内部的数值来确定表面的位置和形状。
简单来说就是遍历每一个栅格,根据每一个栅格的状态去决定其使用的拓扑的结构。
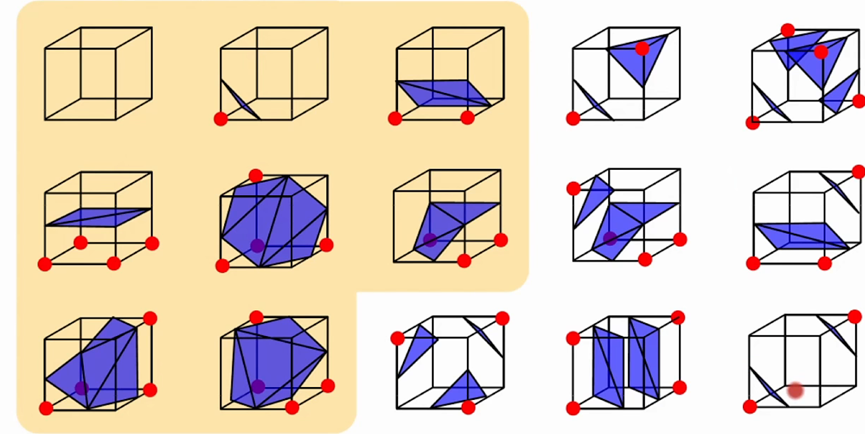
一个立方体有8个点,状态的话有2^8次方个种类,Marching Cubes算法中把种类大概分为上面几种,然后根据状态去选取对应的拓扑结构。
现在目的想要将Marching Cubes方法变成可导的,这样就可以直接从marching cues 提取出来的mesh把它梯度传回前面的这个隐式的表征。
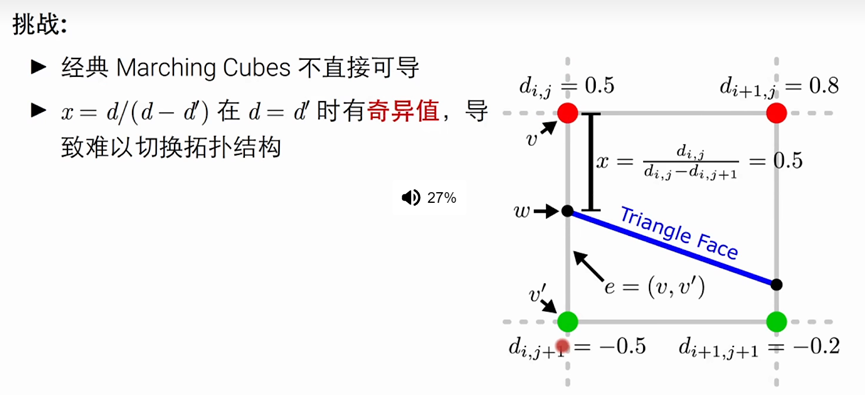
上面提到的Marching Cubes有以上2个困难。
右图中,红色点是表示被占用的,绿色的点是空的。
根据其相邻被占用的状态,我们可以决定不同的topology拓扑取值,然后我们一般通过线性插值来得到其位置
-----公式可以表达为 x=d/(d-d’)
以图中0.5 和-0.5 为例子, x= 0.5/ 1 =0.5,举例d_i_j 0.5单位距离
但是在 d=d’的时候会产生奇异值,导致难以变化拓扑结构
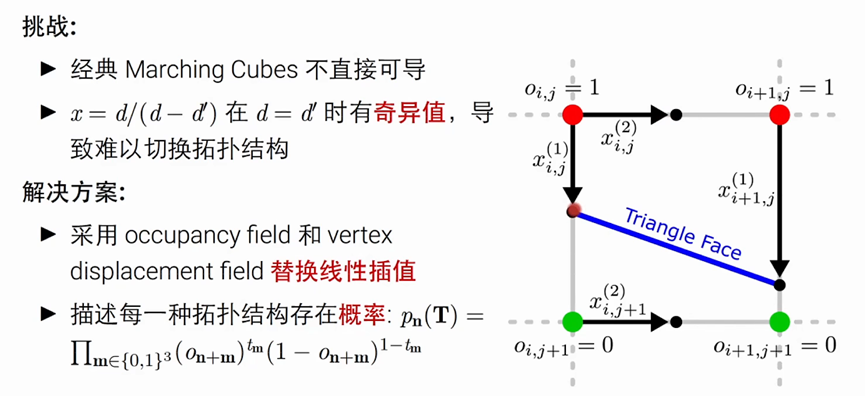
使用 vertex displacement field 替换线性插值
具体解释就是在每一条边都放一个可能交点的位置,再根据occupancy field得到一个概率值
网络结构
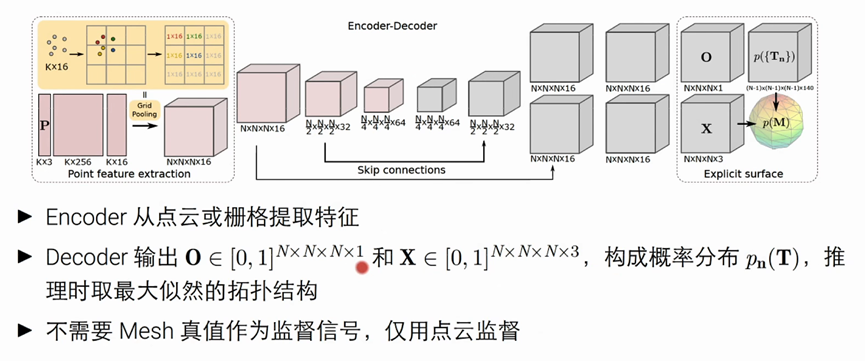
代价函数
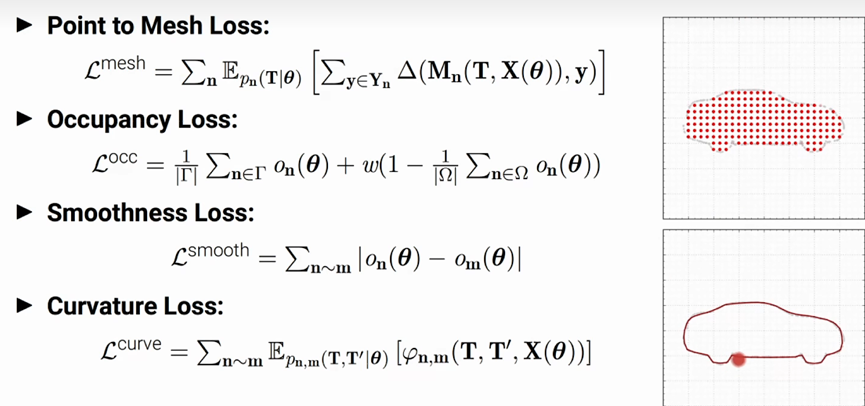
point to mesh loss
occupancy loss:使得场景(车)中间 有一部分是被占用, 四个角是空的
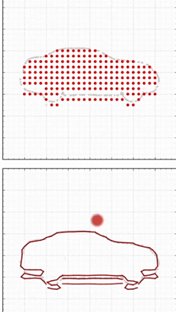
smoothness loss:约束occupancy,让其更平滑
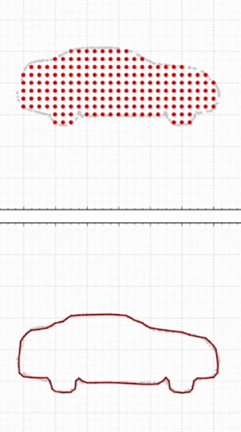
curvature loss: 约束相邻两个车轮间,得到这个面的法向量应该是平滑的,来避免一些崎岖的表面
重建结果

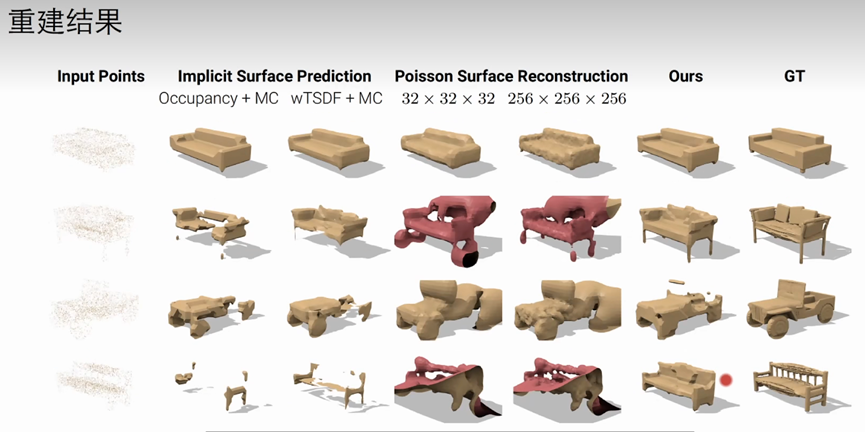
Deep Marching Cubes:Learning Explicit Surface Representations CVPR2018
后续工作
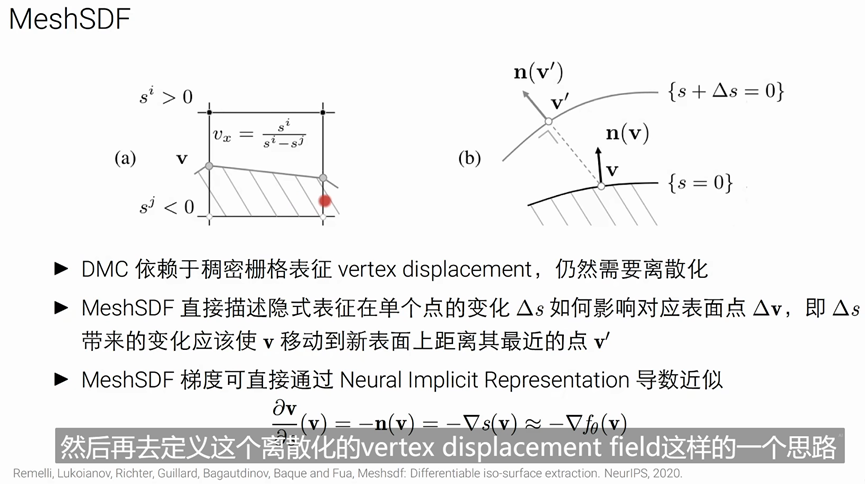
论文: Shape as points : A differentiable poisson solver NeurIPS 2021

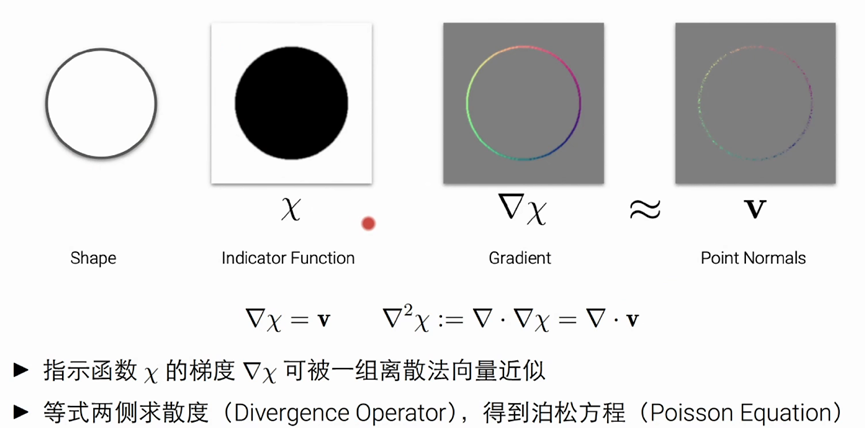
该算法的一个核心思想就是泊松重建:
其indicate function的梯度可以被这个表面的点的法向量来近似,方程如上图(但很难计算)
改进

把泊松方程转换到频域上来求解。
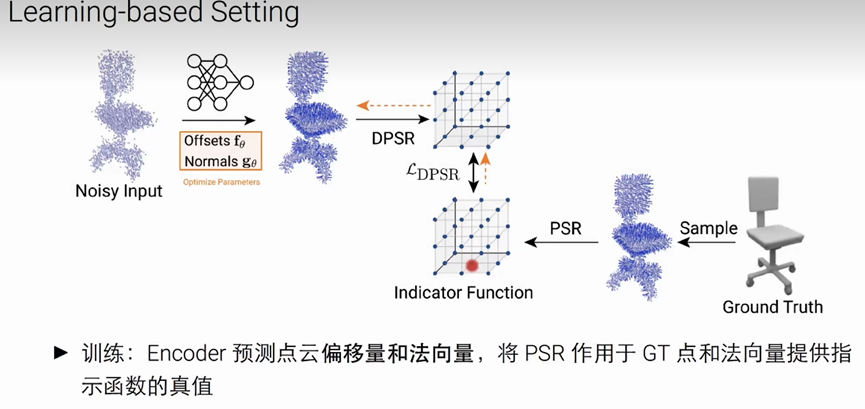
优化过程
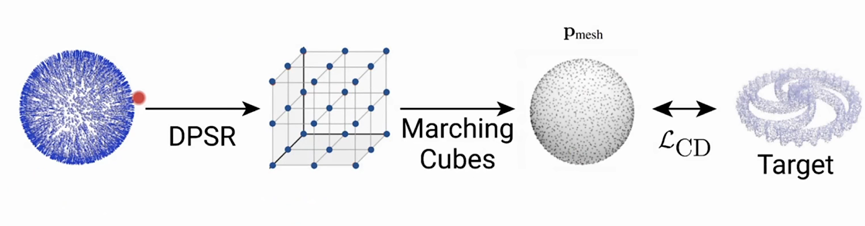
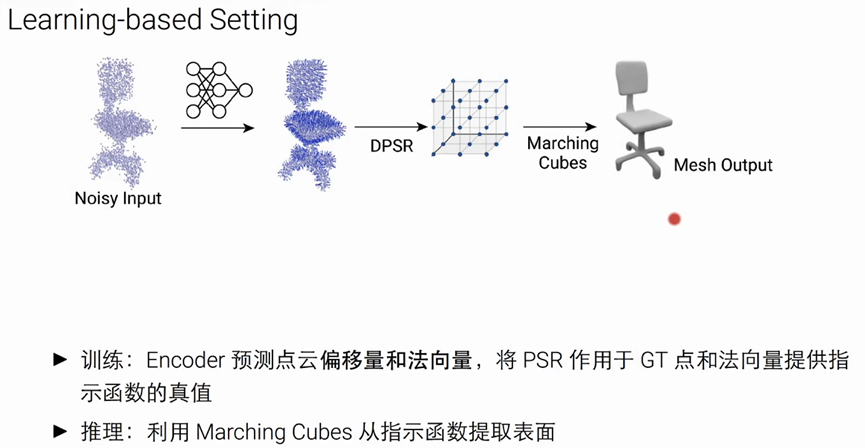
前向传播过程:
采用点云球来初始化(一组点及其法向量)-----使用在频率求解DPSR算法来得到indicator Function(左2图)------通过marching cubes得到指示函数且提出表面------在这个点上去采样,并构造distance loss
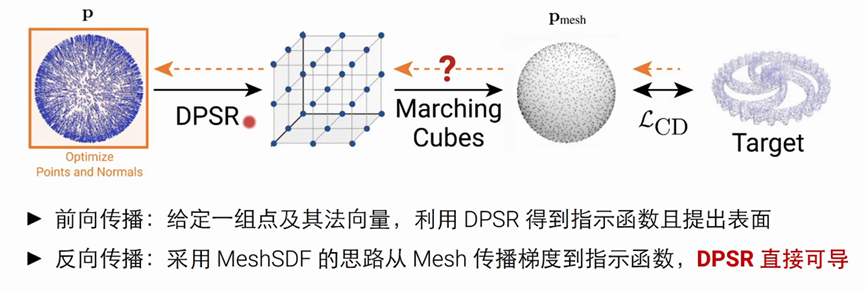
基于learning的方法来重建