代码展示：

class Solution {
    public int rob(int[] nums) {
        int n=nums.length;
        return Math.max(nums[0]+childRob(nums,2,n-2),childRob(nums,1,n-1));
    }
    public int childRob(int[]nums,int left,int right){
        if(left>right){
            return 0;
        }
        int n=nums.length;
        //创建数组
        int[]f=new int[n];  //偷num[i]时所得的最大金额
        int[]g=new int[n];  //不偷num[i]时所得的最大金额
        //初始化
        f[left]=nums[left];
        //填充数组
        for(int i=left+1;i<=right;i++){
            f[i]=nums[i]+g[i-1];
            g[i]=Math.max(f[i-1],g[i-1]);
        }
        //返回值
        return Math.max(f[right],g[right]);
    }

}

        该题其实是Java 动态规划 面试题 17.16. 按摩师的变种，增加了一个首尾是相邻的条件，而我们解决该题也要用到链接的这道题的思想，可以先去看一下上面这篇博客

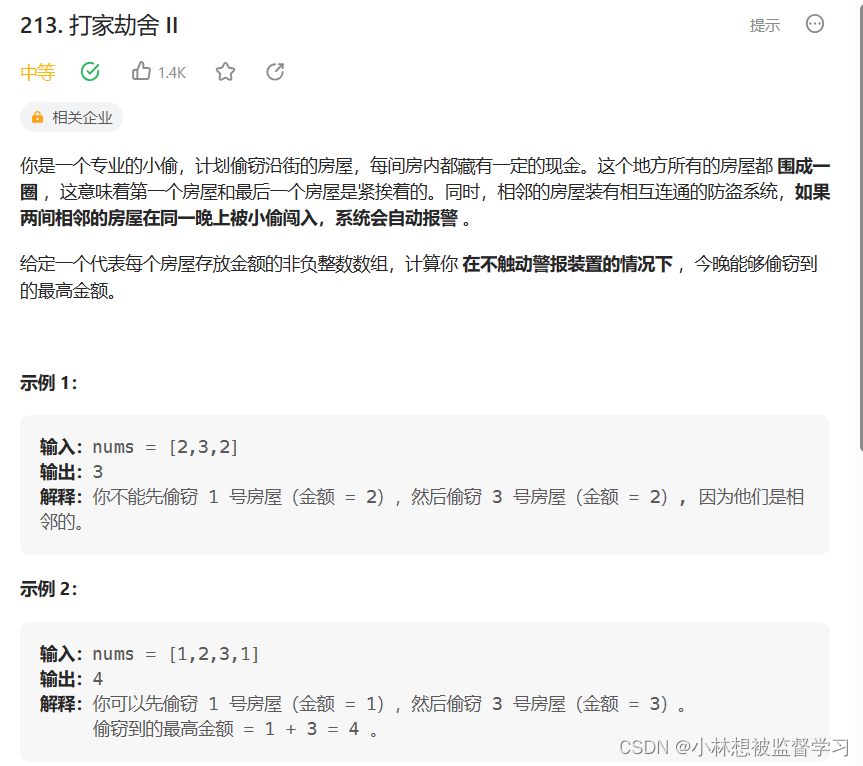
此题可以采用动态规划的方法进行解决，根据解决动态规划题目的5大步骤进行逐步分析

        1.状态表示

                对于一个环形的题目，我们一般要进行分析，根据条件来将环形的问题分解成线性的问题

                由于是首尾之间的联系导致了环形问题的出现，所以我们可以分为两种情况

                        （1）.偷nums[0]

                                此时我们便不能偷nums[1]和nums[n-1],所以此时我们能偷的就只有下标2至n-2，而在2至n-2中便没有了环形关系，此时对数组中2至n-2下标的处理便和Java 动态规划 面试题 17.16. 按摩师的处理一模一样，即此时能偷得的最大金额为nums[0]+childRob(nums,2,n-2)

                        （2）.不偷nums[0]

                                此时对于num[1]和num[n-1]我们可以选择偷或者不偷，说明在1至n-1范围是线性关系，所以我们对数组nums中的下标1至n-1位置进行线性关系的处理即可，即childRob(nums,1,n-1)

        2.状态转移方程

                在childRob中是线性关系，对于i位置我们可以选择偷或者不偷，偷num[i]位置得到的最大金额我们存入f[i]，不偷num[i]位置得到的最大金额我们存入g[i]

                        （1）.偷num[i]位置，偷了num[i]位置我们便不能num，所以我们此时得到的最大金额为 f[i]=nums[i]+g[i-1];

                        (2).不偷num[i]位置，不偷num[i]位置我们可以选择偷num[i-1]的位置，或者不偷，哪种方法得到的金额最大用那种，所以我们此时得到的最大金额为g[i]=Math.max(f[i-1],g[i-1]);

        3.初始化

                由于计算i位置需要依靠i-1位置，所以0下标会越界，初始化0下标即可

        4.填充数组

                根据推出的状态转移方程对数组进行填充

        5.返回值

                由于对于环形的问题我们分为l两种情况，而两种情况中的最大值才是我们需要返回的答案