LRU 算法的淘汰策略是 Least Recently Used,也就是每次淘汰那些最久没被使用的数据;而 LFU 算法的淘汰策略是 Least Frequently Used,也就是每次淘汰那些使用次数最少的数据。
LRU 算法的核心数据结构是使用哈希链表 LinkedHashMap(HashMap + LinkedList),首先借助链表的有序性使得链表元素维持插入顺序,同时借助哈希映射的快速访问能力使得我们可以在 O(1) 时间访问链表的任意元素。
从实现难度上来说,LFU 算法的难度大于 LRU 算法,因为 LRU 算法相当于把数据按照时间排序,这个需求借助链表很自然就能实现,你一直从链表头部加入元素的话,越靠近头部的元素就是新的数据,越靠近尾部的元素就是旧的数据,我们进行缓存淘汰的时候只要简单地将尾部的元素淘汰掉就行了。
而 LFU 算法相当于是把数据按照访问频次进行排序,这个需求恐怕没有那么简单,而且还有一种情况,如果多个数据拥有相同的访问频次,我们就得删除最早插入的那个数据。也就是说 LFU 算法是淘汰访问频次最低的数据,如果访问频次最低的数据有多条,需要淘汰最旧的数据。
所以说 LFU 算法是要复杂很多的,而且经常出现在面试中,因为 LFU 缓存淘汰算法在工程实践中经常使用,也有可能是应该 LRU 算法太简单了。不过话说回来,这种著名的算法的套路都是固定的,关键是由于逻辑较复杂,不容易写出漂亮且没有 bug 的代码。
那么本文就带你拆解 LFU 算法,自顶向下,逐步求精,就是解决复杂问题的不二法门。
一、算法描述
要求你写一个类,接受一个 capacity 参数,实现 get 和 put 方法:
class LFUCache {
// 构造容量为 capacity 的缓存
public LFUCache(int capacity) {}
// 在缓存中查询 key
public int get(int key) {}
// 将 key 和 val 存入缓存
public void put(int key, int val) {}
}
get(key) 方法会去缓存中查询键 key,如果 key 存在,则返回 key 对应的 val,否则返回 -1。
put(key, value) 方法插入或修改缓存。如果 key 已存在,则将它对应的值改为 val;如果 key 不存在,则插入键值对 (key, val)。
当缓存达到容量 capacity 时,则应该在插入新的键值对之前,删除使用频次(后文用 freq 表示)最低的键值对。如果 freq 最低的键值对有多个,则删除其中最旧的那个。
// 构造一个容量为 2 的 LFU 缓存
LFUCache cache = new LFUCache(2);
// 插入两对 (key, val),对应的 freq 为 1
cache.put(1, 10);
cache.put(2, 20);
// 查询 key 为 1 对应的 val
// 返回 10,同时键 1 对应的 freq 变为 2
cache.get(1);
// 容量已满,淘汰 freq 最小的键 2
// 插入键值对 (3, 30),对应的 freq 为 1
cache.put(3, 30);
// 键 2 已经被淘汰删除,返回 -1
cache.get(2);
二、思路分析
一定先从最简单的开始,根据 LFU 算法的逻辑,我们先列举出算法执行过程中的几个显而易见的事实:
- 调用 get(key) 方法时,要返回该 key 对应的 val。
- 只要用 get 或者 put 方法访问一次某个 key,该 key 的 freq 就要加一。
- 如果在容量满了的时候进行插入,则需要将 freq 最小的 key 删除,如果最小的 freq 对应多个
key,则删除其中最旧的那一个。
好的,我们希望能够在 O(1) 的时间内解决这些需求,可以使用基本数据结构来逐个击破:
- 使用一个 HashMap 存储 key 到 val 的映射,就可以快速计算 get(key)。
HashMap<Integer, Integer> keyToVal; - 使用一个 HashMap 存储 key 到 freq 的映射,就可以快速操作 key 对应的 freq。
HashMap<Integer, Integer> keyToFreq; - 这个需求应该是 LFU 算法的核心,所以我们分开说。
3.1. 首先,肯定是需要 freq 到 key 的映射,用来找到 freq 最小的 key。
3.2. 将 freq 最小的 key 删除,那你就得快速得到当前所有 key 最小的 freq 是多少。想要时间复杂度 O(1) 的话,肯定不能遍历一遍去找,那就用一个变量 minFreq 来记录当前最小的 freq 吧。
3.3.可能有多个 key 拥有相同的 freq,所以 freq 对 key 是一对多的关系,即一个 freq 对应一个 key 的列表。
3.4. 希望 freq 对应的 key 的列表是存在时序的,便于快速查找并删除最旧的 key。
3.5. 希望能够快速删除 key 列表中的任何一个 key,因为如果频次为 freq 的某个 key 被访问,那么它的频次就会变成 freq+1,就应该从 freq 对应的 key 列表中删除,加到 freq+1 对应的 key 的列表中。
HashMap<Integer, LinkedHashSet> freqToKeys;
int minFreq = 0;
介绍一下这个 LinkedHashSet,它满足我们 3.3,3.4,3.5 这几个要求。你会发现普通的链表 LinkedList 能够满足 3.3,3.4 这两个要求,但是由于普通链表不能快速访问链表中的某一个节点,所以无法满足 3.5 的要求。
LinkedHashSet 顾名思义,是链表和哈希集合的结合体。链表不能快速访问链表节点,但是插入元素具有时序;哈希集合中的元素无序,但是可以对元素进行快速的访问和删除。
那么,它俩结合起来就兼具了哈希集合和链表的特性,既可以在 O(1) 时间内访问或删除其中的元素,又可以保持插入的时序,高效实现 3.5 这个需求。
综上,我们可以写出 LFU 算法的基本数据结构:
class LFUCache {
// key 到 val 的映射,我们后文称为 KV 表
HashMap<Integer, Integer> keyToVal;
// key 到 freq 的映射,我们后文称为 KF 表
HashMap<Integer, Integer> keyToFreq;
// freq 到 key 列表的映射,我们后文称为 FK 表
HashMap<Integer, LinkedHashSet<Integer>> freqToKeys;
// 记录最小的频次
int minFreq;
// 记录 LFU 缓存的最大容量
int cap;
public LFUCache(int capacity) {
keyToVal = new HashMap<>();
keyToFreq = new HashMap<>();
freqToKeys = new HashMap<>();
this.cap = capacity;
this.minFreq = 0;
}
public int get(int key) {}
public void put(int key, int val) {}
}
三、代码框架
LFU 的逻辑不难理解,但是写代码实现并不容易,因为你看我们要维护 KV 表,KF 表,FK 表三个映射,特别容易出错。对于这种情况,labuladong 教你三个技巧:
-
不要企图上来就实现算法的所有细节,而应该自顶向下,逐步求精,先写清楚主函数的逻辑框架,然后再一步步实现细节。
-
搞清楚映射关系,如果我们更新了某个 key 对应的 freq,那么就要同步修改 KF 表和 FK 表,这样才不会出问题。
-
画图,画图,画图,重要的话说三遍,把逻辑比较复杂的部分用流程图画出来,然后根据图来写代码,可以极大减少出错的概率。
下面我们先来实现 get(key) 方法,逻辑很简单,返回 key 对应的 val,然后增加 key 对应的 freq:
public int get(int key) {
if (!keyToVal.containsKey(key)) {
return -1;
}
// 增加 key 对应的 freq
increaseFreq(key);
return keyToVal.get(key);
}
增加 key 对应的 freq 是 LFU 算法的核心,所以我们干脆直接抽象成一个函数 increaseFreq,这样 get 方法看起来就简洁清晰了对吧。
下面来实现 put(key, val) 方法,逻辑略微复杂,我们直接画个图来看:
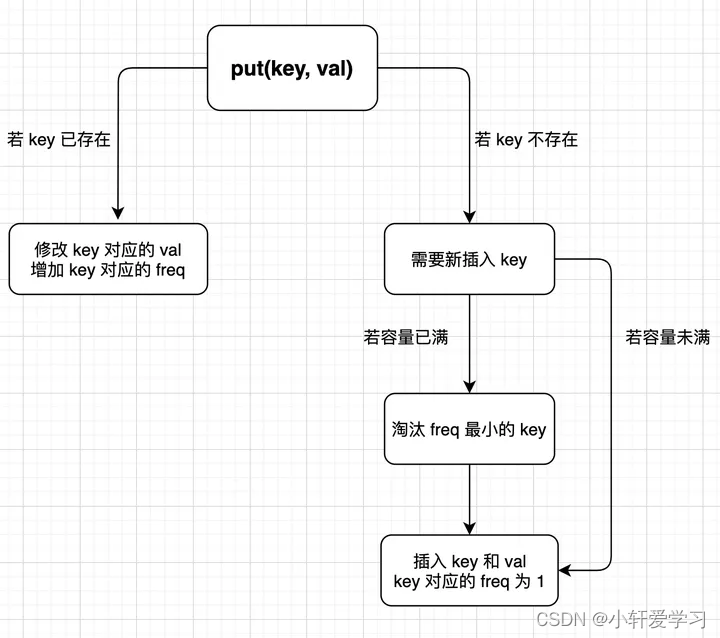
这图就是随手画的,不是什么正规的程序流程图,但是算法逻辑一目了然,看图可以直接写出 put 方法的逻辑:
public void put(int key, int val) {
if (this.cap <= 0) return;
/* 若 key 已存在,修改对应的 val 即可 */
if (keyToVal.containsKey(key)) {
keyToVal.put(key, val);
// key 对应的 freq 加一
increaseFreq(key);
return;
}
/* key 不存在,需要插入 */
/* 容量已满的话需要淘汰一个 freq 最小的 key */
if (this.cap <= keyToVal.size()) {
removeMinFreqKey();
}
/* 插入 key 和 val,对应的 freq 为 1 */
// 插入 KV 表
keyToVal.put(key, val);
// 插入 KF 表
keyToFreq.put(key, 1);
// 插入 FK 表
freqToKeys.putIfAbsent(1, new LinkedHashSet<>());
freqToKeys.get(1).add(key);
// 插入新 key 后最小的 freq 肯定是 1
this.minFreq = 1;
}
increaseFreq 和 removeMinFreqKey 方法是 LFU 算法的核心,我们下面来看看怎么借助 KV 表,KF 表,FK 表这三个映射巧妙完成这两个函数。
四、LFU 核心逻辑
首先来实现 removeMinFreqKey 函数:
private void removeMinFreqKey() {
// freq 最小的 key 列表
LinkedHashSet<Integer> keyList = freqToKeys.get(this.minFreq);
// 其中最先被插入的那个 key 就是该被淘汰的 key
int deletedKey = keyList.iterator().next();
/* 更新 FK 表 */
keyList.remove(deletedKey);
if (keyList.isEmpty()) {
freqToKeys.remove(this.minFreq);
// 问:这里需要更新 minFreq 的值吗?
}
/* 更新 KV 表 */
keyToVal.remove(deletedKey);
/* 更新 KF 表 */
keyToFreq.remove(deletedKey);
}
删除某个键 key 肯定是要同时修改三个映射表的,借助 minFreq 参数可以从 FK 表中找到 freq 最小的 keyList,根据时序,其中第一个元素就是要被淘汰的 deletedKey,操作三个映射表删除这个 key 即可。
但是有个细节问题,如果 keyList 中只有一个元素,那么删除之后 minFreq 对应的 key 列表就为空了,也就是 minFreq 变量需要被更新。如何计算当前的 minFreq 是多少呢?
实际上没办法快速计算 minFreq,只能线性遍历 FK 表或者 KF 表来计算,这样肯定不能保证 O(1) 的时间复杂度。
但是,其实这里没必要更新 minFreq 变量,因为你想想 removeMinFreqKey 这个函数是在什么时候调用?在 put 方法中插入新 key 时可能调用。而你回头看 put 的代码,插入新 key 时一定会把 minFreq 更新成 1,所以说即便这里 minFreq 变了,我们也不需要管它。
下面来实现 increaseFreq 函数:
private void increaseFreq(int key) {
int freq = keyToFreq.get(key);
/* 更新 KF 表 */
keyToFreq.put(key, freq + 1);
/* 更新 FK 表 */
// 将 key 从 freq 对应的列表中删除
freqToKeys.get(freq).remove(key);
// 将 key 加入 freq + 1 对应的列表中
freqToKeys.putIfAbsent(freq + 1, new LinkedHashSet<>());
freqToKeys.get(freq + 1).add(key);
// 如果 freq 对应的列表空了,移除这个 freq
if (freqToKeys.get(freq).isEmpty()) {
freqToKeys.remove(freq);
// 如果这个 freq 恰好是 minFreq,更新 minFreq
if (freq == this.minFreq) {
this.minFreq++;
}
}
}
更新某个 key 的 freq 肯定会涉及 FK 表和 KF 表,所以我们分别更新这两个表就行了。
和之前类似,当 FK 表中 freq 对应的列表被删空后,需要删除 FK 表中 freq 这个映射。如果这个 freq 恰好是 minFreq,说明 minFreq 变量需要更新。
能不能快速找到当前的 minFreq 呢?这里是可以的,因为我们刚才把 key 的 freq 加了 1 嘛,所以 minFreq 也加 1 就行了。
至此,经过层层拆解,LFU 算法就完成了。