代码：VoxelNet: https://github.com/skyhehe123/VoxelNet-pytorch
论文：VoxelNet End-to-End Learning for Point Cloud Based 3D Object Detection

1. 解决了什么问题？

对点云做 3D 检测是许多应用得以落地的关键，如自动驾驶和扫地机器人等。与图像检测相比，LiDAR 能提供可靠的深度信息，准确地定位目标，描述物体的形状。但由于多种因素，如 3D 空间的非均匀采样、传感器的有效范围、遮挡和相对位姿，LiDAR 点云一般是非常稀疏的，点云密度也会剧烈变化。为了解决上述问题，我们要人为设计一种特征表示。

2. 提出了什么方法？

本文摒弃了 3D 点云的特征工程，提出了 VoxelNet，该 3D 检测网络以端到端的形式，同时学习提取点云的特征和预测 3D 边框。VoxelNet 将 3D 点云划分为相同空间大小的 3D 体素，然后通过体素特征编码层（VFE）将每个体素内的点云变换成统一的特征表示。通过多个 VFE 层，就能学到复杂的特征来描述局部的 3D 形状信息。最后，再将该特征输入 RPN，生成预测结果。

2.1 VoxelNet 架构

如下图所示，VoxelNet 包括三个功能模块：特征学习网络、卷积中间层和 RPN。特征学习网络的输入是原始点云，将空间划分成体素，将每个体素内的点变换成向量表示，以此描述物体的形状信息。该空间用稀疏的 4D 张量表示。然后，将稀疏的 4D 张量输入卷积中间层，聚合空间上下文信息。最终，用一个 RPN 输出 3D 检测结果。

2.1.1 特征学习网络

Voxel Partition

给定点云，将 3D 空间划分为相同体积大小的体素。假设点云包括的是大小为 $D,H,W$ 的 3D 空间，分别对应 $Z,Y,X$ 轴。定义每个体素的大小是 $v_D,v_H,v_W$。则 3D 体素网格的大小是$D^{\prime }=D/v_D,H^{\prime }=H/v_H,W^{\prime }=W/v_W$。这里，我们假设 $D,H,W$ 是 $v_D,v_H,v_W$ 的倍数。

Grouping
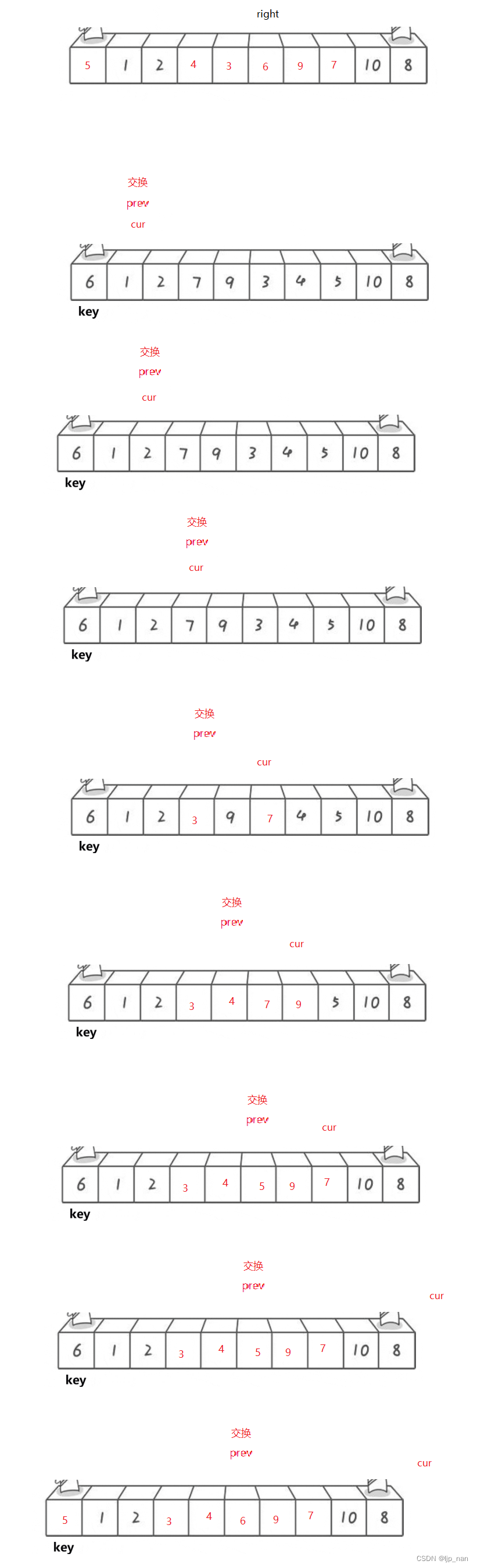
根据点云所在的体素，将它们分组。由于距离、遮挡、目标姿态以及非均匀采样，LiDAR 点云会非常稀疏，点云的密度也会剧烈变化。因此，分组后，一个体素可能包含不同个数的点。如上图所示，体素-$1$里面的点个数明显多于体素-$2$和体素-$4$，体素-$3$里面没有点。

Random Sampling
通常，一个高清晰度的点云会包括约 $10$ 万个点。直接处理所有的点会带来极高的计算成本，而且空间中点云密度差异大也会使检测结果带有偏见。因此，如果某体素内的点的个数超过了$T$，我们就随机采样 $T$ 个点。该策略既可以节约计算成本，也可缓解体素内点云数量的不均衡性，减轻采样偏见的问题。

Stacked Voxel Feature Encoding
本文关键的创新就是 stacked VFE 层。上图展示了每个体素的层级特征编码过程。本文在后续部分用 VFE Layer-1 来介绍。下图展示了 VFE Layer-1 的结构。

用 $\mathbf{V}={\left\{{\mathbf{p}}_i=[x_i,y_i,z_i,r_i{]}^T\in {\mathbb{R}}^4\right\}}_{i=\mathrm{1...}t}$ 表示一个包含了 $t\le T$ 个 LiDAR 点的非空体素，${\mathbf{p}}_i$ 为第 $i$ 个点的 $XYZ$ 坐标，$r_i$ 是反射率。

• 首先计算 $\mathbf{V}$ 内所有点的 centroid，作为局部均值，记作 $(v_x,v_y,v_z)$。
• 然后用相对于 centroid 的偏移量来增广每个点 ${\mathbf{p}}_i$，得到输入特征的集合 ${\mathbf{V}}_{in}={\left\{{\hat{\mathbf{p}}}_i=[x_i,y_i,z_i,r_i,x_i-v_x,y_i-v_y,z_i-v_z{]}^T\in {\mathbb{R}}^7\right\}}_{i=\mathrm{1...}t}$.
• 然后，用全连接网络将 ${\mathbf{V}}_{in}$ 里的每个 ${\mathbf{p}}_i$ 变换到特征空间，在特征空间内从点特征 ${\mathbf{f}}_i\in {\mathbb{R}}^m$ 聚合信息，编码每个体素的表面形状。该全连接网络包括一个线性层、BN 层和 ReLU 层。得到点特征表示后，对所有的 ${\mathbf{f}}_i$ 做 $\text{MaxPool}$ 操作，得到 $\mathbf{V}$ 的局部聚合特征 $\tilde{\mathbf{f}}\in {\mathbb{R}}^m$。最后，用 $\tilde{\mathbf{f}}$ 来增强每个 ${\mathbf{f}}_i$，得到 ${\mathbf{f}}_i^{out}=[{\mathbf{f}}_i^T,{\tilde{\mathbf{f}}}^T{]}^T\in {\mathbb{R}}^{2m}$，该操作是 pointwise concat。因此，我们就得到了输出特征集合 V o u t = { f i o u t } i . . . t \mathbf{V}_{out}=\left\{\mathbf{f}_i^{out}\right\}_{i...t} Vout​={fiout​}i...t​。

所有的非空体素的编码方式都一样，共享全连接网络的参数。

使用 VFE-$i(c_{in},c_{out})$ 来表示第 $i$ 个 VFE 层，它将维度为 $c_{in}$ 的输入特征变换到维度是$c_{out}$的输出特征。线性层学习一个大小是 $c_{in}\times (c_{out}/2)$ 的矩阵，pointwise concat 操作输出的维度就是 $c_{out}$。

由于输出特征结合了点特征和局部聚合特征，stacking VFE 层就编码了体素内各点之间的关系，最终的特征表示就能描述形状的信息。通过将 VFE-$n$ 的输出变换到${\mathbb{R}}^C$空间，得到体素特征，然后使用逐元素的$\text{MaxPool}$操作，其中$C$是体素特征的维度。

Sparse Tensor Representation
只对非空体素做处理，我们得到一组体素特征，每个特征都关联着唯一的非空体素。该组体素特征可用一个稀疏的 4D 张量表示，大小是$C\times D^{\prime }\times H^{\prime }\times W^{\prime }$。尽管点云包含约$10$万个点，但超过$90\%$的体素通常是空的。将非空体素表示为稀疏的张量，极大地降低了内存占用和计算成本，实现起来效率就比较高。

2.1.2 卷积中间层

我们用$\text{Conv}M\mathbf{D}(c_{in},c_{out},\mathbf{k},\mathbf{s},\mathbf{p})$来表示$M$维的卷积操作，$c_{in},c_{out}$是输入和输出通道数，$\mathbf{k},\mathbf{s},\mathbf{p}$是$M$维向量对应的卷积核大小、步长和 padding 大小。这里$M=3$。如果对于 $M$ 维向量，卷积核大小都是一样的，则用一个标量$k$ 来表示，即 $\mathbf{k}=(k,k,k)$。
假设输入的张量形状是 $(N,C_{in},D_{in},H_{in},W_{in})$，输出的张量形状是 $(N,C_{out},D_{out},H_{out},W_{out})$，计算过程如下：
$$D_{out}=\lfloor \frac{D_{in}+2\times \text{padding}[0]-\text{dilation}[0]\times (\text{kernel\_size}[0]-1)-1}{\text{stride}[0]}+1\rfloor$$
$$H_{out}=\lfloor \frac{H_{in}+2\times \text{padding}[1]-\text{dilation}[1]\times (\text{kernel\_size}[1]-1)-1}{\text{stride}[1]}+1\rfloor$$
$$W_{out}=\lfloor \frac{W_{in}+2\times \text{padding}[2]-\text{dilation}[2]\times (\text{kernel\_size}[2]-1)-1}{\text{stride}[2]}+1\rfloor$$

每个卷积中间层都包括 3D 卷积、BN 层和 ReLU 层。卷积中间层的感受野是逐渐增大的，在形状描述信息内增加上下文信息，以此聚合体素特征。

2.1.3 RPN

RPN 已经成为先进的目标检测方法必备的构建模块。本文，作者对 RPN 做了几点改进，将它和特征学习网络与卷积中间层结合，以端到端的方式训练。

RPN 的输入是卷积中间层的特征图，结果如下图所示。网络有三个全卷积模块。每个模块的第一层会通过步长$2$的卷积来下采样特征图，后面是步长为$1$的一组卷积。每个卷积层后面跟着一个 BN 层和 ReLU 操作。然后将每个模块的输出上采样到固定大小，然后 concat 到一起，得到高分辨率的特征图。最后，将特征图映射到概率得分图和回归图。

2.2 损失函数

{ a i p o s } i = 1... N p o s \left\{a_i^{pos}\right\}_{i=1...N_{pos}} {aipos​}i=1...Npos​​表示 $N_{pos}$个正的 anchors，${\left\{a_j^{neg}\right\}}_{j=\mathrm{1...}{N}_{neg}}$表示$N_{neg}$个负的 anchors。用$(x_c^g,y_c^g,z_c^g,l^g,w^g,h^g,{\theta }^g)$表示一个 ground-truth 3D 框，其中$x_c^g,y_c^g,z_c^g$表示中心位置，$l^g,w^g,h^g$表示边框的长度、宽度和高度，${\theta }^g$是围绕$Z$轴的偏航角。用$(x_c^a,y_c^a,z_c^a,l^a,w^a,h^a,{\theta }^a)$ 表示一个正的 anchor，定义残差向量${\mathbf{u}}^{\ast }\in {\mathbb{R}}^7$包含7个回归目标，分别对应中心位置$\Delta x,\Delta y,\Delta z$，三个尺寸$\Delta l,\Delta w,\Delta h$，以及旋转角度$\Delta \theta$，计算如下：

$$\Delta x=\frac{x_c^g-x_c^a}{d^a},\Delta y=\frac{y_c^g-y_c^a}{d^a},\Delta z=\frac{z_c^g-z_c^a}{h^a}$$
$$\Delta l=\log \frac{l^g}{l^a},\Delta w=\log \frac{w^g}{w^a},\Delta h=\log \frac{h^g}{h^a}$$
$$\Delta \theta ={\theta }^g-{\theta }^a$$

其中，$d^a=\sqrt{(l^a{)}^2+(w^a{)}^2}$ 是 anchor box 的对角线长度。这里，我们目的是直接预测带朝向的 3D 框，用对角线$d^a$来归一化$\Delta x$和$\Delta y$。损失函数如下：

$$L=\alpha \frac{1}{N_{pos}}\sum _i{L}_{cls}(p_i^{pos},1)+\beta \frac{1}{N_{neg}}\sum _j{L}_{cls}(p_j^{neg},0)+\frac{1}{N_{pos}}\sum _i{L}_{reg}({\mathbf{u}}_i,{\mathbf{u}}_i^{\ast })$$

其中，$p_i^{pos}$和$p_j^{neg}$表示正负样本 $a_i^{pos}$ 和 $a_i^{neg}$ 的 softmax 输出，而 ${\mathbf{u}}_i\in {\mathbb{R}}^7$ 和 ${\mathbf{u}}_i^{\ast }\in {\mathbb{R}}^7$ 表示正样本 $a_i^{pos}$ 的回归预测和 ground-truth。前两项损失是归一化的分类损失，$L_{cls}$ 是二元交叉熵损失，$\alpha >0,\beta >0$ 用于平衡正负样本。$L_{reg}$是回归损失，使用的是 SmoothL1 函数。

2.3 高效实现

GPU 对于密集张量做了特殊优化，但要想直接应用到点云上有个问题，即点云是稀疏分布的，每个体素内的点云个数都不一样。作者设计了一个方法将点云转换为密集张量的结构，从而 stacked VFE 操作可以做到对点云和体素的并行计算。

在下图中，作者介绍了该方法。首先，初始化一个$K\times T\times 7$的张量，存储体素输入特征缓存，$K$是非空体素的最大个数，$T$是每个体素内点的最大个数，$7$是每个输入点的编码维度。在开始处理前，随机化这些点。对点云内的每个点，检查它对应的体素是否存在。这个查询操作实现起来很高效，复杂度为 $O(1)$。在哈希表中，哈希 key 是每个体素的坐标。如果一个体素已经初始化过了，如果它有$<T$个点，就将点插入到该体素位置。如果体素没有初始化，则初始化一个新的体素，将体素坐标存储在体素坐标缓存里面，并把点插入到这个体素位置。过一遍所有的点表就可以构建出体素的输入特征和坐标缓存，因此复杂度是 $O(n)$。为了进一步提升效率，我们可以忽略掉那些点较少的体素，只存储有限个数的体素（$K$）。

体素输入缓存构建完成后，stacked VFE 只涉及了点操作和体素操作，可以在 GPU 上并行实现。最后，通过存储的坐标缓存，我们将稀疏的体素结构重新组织成密集的体素网格。后续卷积中间层和 RPN 就在这个密集的体素网格上操作，可以用 GPU 高效实现。

3. 训练细节

3.1 网络细节

在 KITTI 数据集上做的实验。

Car Detection

对于该任务，点云的范围是 $[-3,1]\times [-40,40]\times [0,70.4]$ 米，分别对应$Z,Y,X$轴。舍弃那些投影到图像边界以外的点云。体素大小设置为$v_D=0.4,v_H=0.2,v_W=0.2$ 米，这样就有 $D^{\prime }=10,H^{\prime }=400,W^{\prime }=352$。在每个非空体素内，随机选取 $T=35$ 个点。使用两个 VFE 层 VFE-1($7,32$) 和 VFE-2($32,128$)。最后全连接网络将 VFE-2 的输出映射到 ${\mathbb{R}}^{128}$ 空间。因此，该特征学习网络就产生一个稀疏张量，大小是 $128\times 10\times 400\times 352$。为了聚合体素特征，使用三个卷积中间层，$\text{Conv3D}(128,64,3,(2,1,1),(1,1,1)),\text{Conv3D}(64,64,3,(1,1,1),(0,1,1)),\text{Conv3D}(64,64,3,(2,1,1),(1,1,1))$，输出一个 4D 张量，形状是 $64\times 2\times 400\times 352$。

Reshape 后，输入 RPN 的特征图大小是 $128\times 400\times 352$，维度分别是 3D 张量的通道数、高度和宽度。上图展示了细节信息。本文只使用了一个 anchor 大小，$l^a=3.9,w^a=1.6,h^a=1.56$ 米，中心点高度是 $z_c^a=-1.0$ 米，有两个偏航角 $0$ 和 $90$ 度。Anchor 匹配策略如下：如果它和某个 ground-truth 框的 IoU 是最大的，或者它们的 IoU $>0.6$，则它就是正样本。如果它和所有的 ground-truth 框的 IoU 都 $<0.45$，则它就是负样本。忽略那些与任何 ground-truth 都 $0.45<\text{IoU}\le 0.6$的样本。另外，在 $L=\alpha \frac{1}{N_{pos}}{\sum }_i{L}_{cls}(p_i^{pos},1)+\beta \frac{1}{N_{neg}}{\sum }_j{L}_{cls}(p_j^{neg},0)+\frac{1}{N_{pos}}{\sum }_i{L}_{reg}({\mathbf{u}}_i,{\mathbf{u}}_i^{\ast })$ 中，$\alpha =1.5,\beta =1$。

Pedestrian and Cyclist Detection

输入范围是$[-3,1]\times [-20,20]\times [0,48]$ 米，分别对应$Z,Y,X$轴。使用与 Car 相同的体素大小，就有 $D=10,H=200,W=240$。设置 $T=45$ 以获取更多的 LiDAR 点，更好地描述形状信息。特征学习网络和卷积中间层和 Car 检测任务用的是一样的。在 RPN 中，修改了 $\text{block 1}$，将第一个 2D 卷积的步长大小从$2$改为了$1$。这样在样本匹配时，分辨率就更细致一些，对于行人和骑车人来说更必要。Anchor 大小为 $l^a=0.8,w^a=0.6,h^a=1.73$ 米，中心点高度是 $z_c^a=-0.6$ 米。Anchor 匹配策略如下：如果它和某个 ground-truth 框的 IoU 是最大的，或者它们的 IoU $>0.5$，则它就是正样本。如果它和所有的 ground-truth 框的 IoU 都 $<0.35$，则它就是负样本。忽略那些与任何 ground-truth 都 $0.35<\text{IoU}\le 0.5$的样本。

训练时，使用 SGD 优化器，前$150$个 epochs，它的学习率是 $0.01$，后面的 $10$ 个 epochs 学习率衰减至 $0.001$。Batch size 为 $16$。

3.2 数据增强

因为只有不足$4000$个点云，从头训练的话会造成过拟合。于是，作者引入了三种数据增强方法。增强训练数据非常快，所以无需存储在磁盘上。

$\mathbf{M}={\left\{{\mathbf{p}}_i=[x_i,y_i,z_i,r_i{]}^T\in {\mathbb{R}}^4\right\}}_{i=1,...,N}$ 是所有的点云，包括$N$个点。将 3D 框${\mathbf{b}}_i$记作 $(x_c,y_c,z_c,l,w,h,\theta )$，其中$x_c,y_c,z_c$是中心位置，$l,w,h$是长宽高，$\theta$是偏航角。${\mathbf{b}}_i$ 内所有的 LiDAR 点记作 Ω i = { p ∣ x ∈ [ x c − l / 2 , x c + l / 2 ] , y ∈ [ y c − w / 2 , y c + w / 2 ] , z ∈ [ z c − h / 2 , z c + h / 2 ] , p ∈ M } \Omega_i=\left\{\mathbf{p}|x \in [x_c-l/2, x_c + l/2], y\in [y_c-w/2, y_c+w/2], z\in [z_c-h/2, z_c+h/2], \mathbf{p\in M}\right\} Ωi​={p∣x∈[xc​−l/2,xc​+l/2],y∈[yc​−w/2,yc​+w/2],z∈[zc​−h/2,zc​+h/2],p∈M}，其中$\mathbf{p}=[x,y,z,r]$ 表示 $\mathbf{M}$ 里面某个 LiDAR 点。

第一种数据增强就是对每个 3D 框及其里面的 LiDAR 点做扰动。以随机变量 $\Delta \theta \in [-\pi /10,+\pi /10]$，关于 $(x_c,y_c,z_c)$ ，围绕$Z$轴旋转 3D 框 ${\mathbf{b}}_i$，以及 ${\Omega }_i$。然后对 ${\mathbf{b}}_i$ 和 ${\Omega }_i$ 里的点都分别增加一个偏移量 $\Delta x,\Delta y,\Delta z$。$\Delta x,\Delta y,\Delta z$ 是从均值为$0$，标准差为 $1.0$的高斯分布中随机选取的。如果两个边框在做了扰动后，发生了相互碰撞，则回退到原来的情形。因为扰动是独立地作用在每个 ground-truth 框和关联的 LiDAR 点上的，网络可以更有效地学习。

第二种方法就是全局缩放所有的 ground-truth 边框 ${\mathbf{b}}_i$ 以及所有的点云 $\mathbf{M}$。将 $XYZ$ 坐标系、 ${\mathbf{b}}_i$ 的三个维度以及所有点的坐标都乘以一个来自于 $[0.95,1.05]$ 均匀分布的随机数。这个增强方法提升了网络的鲁棒性，可以检测不同大小的目标。

最后一个方法就是对所有的 ground-truth 框 ${\mathbf{b}}_i$ 和整体点云 $\mathbf{M}$ 使用全局旋转。沿着 $Z$ 轴在原点位置旋转。从均匀分布 $[-\pi /4,+\pi /4]$ 随机选取全局旋转的偏移量。通过旋转点云，我们可以模拟车辆转弯的样子。