Differentially Private Compressive K-means
Differentially Private Compressive K-means | IEEE Conference Publication | IEEE Xplore
摘要:
介绍
在过去的几十年中,数据集的大小和可用性呈指数级增长。虽然这些数据有望取得重大进展,但其庞大的规模带来了挑战,需要新的机器学习方法能够在时间和内存上有效处理大型数据集。除了可处理性问题之外,使用和发布这些数据还引发了严重的隐私问题,因此需要机器学习算法来保证用户的隐私。
在压缩学习框架[1]中,数据集被压缩为广义随机矩向量(有时称为草图),然后可以使用大大减少的计算资源来执行学习阶段。在本文中,我们提出了一种基于这种方法的机制,通过计算数据集子样本的噪声时刻,从具有可证明隐私保证的压缩数据集中学习。该机制被证明可以提供差异隐私[2],这是 Dwork 等人提出的一种流行的隐私定义。非正式地说,它确保机器学习算法的输出不依赖于数据集中某个人的存在。
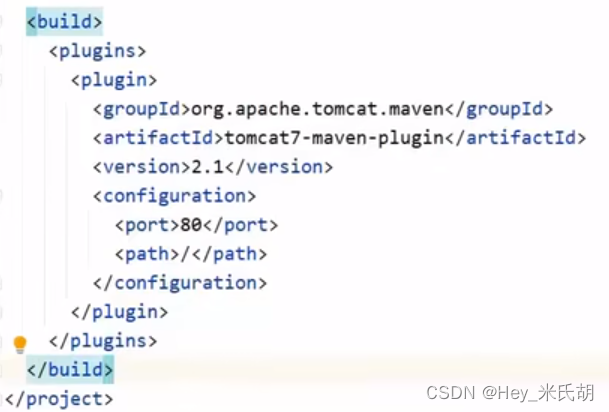
我们的方法在分布式环境中运行,其中数据集在多个设备之间共享,每个设备一劳永逸地公开发布和公开发布其有权访问的数据的混乱草图。这可以即时完成,并且内存消耗低。然后,中央分析师将每台设备的草图平均化为一个全局乱序草图,稍后将其用于机器学习任务。学习任务被表述为传统压缩学习中的逆问题。虽然本文重点关注k-意味着聚类,我们的方法是通用的,可以很容易地应用于其他学习任务,例如高斯混合建模或主成分分析。在聚类的情况下,我们证明了噪声草图的效用,即其后续学习的质量,可以通过信噪比来衡量;我们用这个量来解释隐私和实用性之间存在的权衡,并激励我们选择参数。
我们在第 2 节中给出了k均值聚类、压缩学习和差分隐私的一些背景知识,并在第 3 节中介绍了我们的攻击模型和数据发布机制。第4节和第5节分别提供了隐私保证和效用措施,第6节讨论了两者之间的权衡,第7节介绍了相关工作。
符号和背景

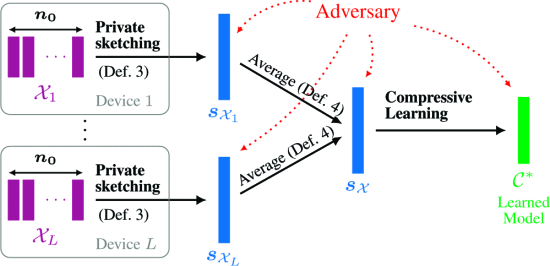
 差异隐私被广泛认为是一种强有力且特别保守的隐私定义。根据定义,它可以保护记录的隐私,即使对手知道数据集中的所有其他记录。此外,它已被证明可以抵抗多种类型的攻击[9]。形式上,我们的定义提供了事件级 DP [10],如果每个人在数据集中只有一条记录,则相当于用户级。然而,为通用分析实施差异化私有机制仍然是一个公开的挑战[11]。尽管无法再从(乱序的)草图计算一些统计数据,但我们的机制仍然允许解决多个学习任务[1]。
差异隐私被广泛认为是一种强有力且特别保守的隐私定义。根据定义,它可以保护记录的隐私,即使对手知道数据集中的所有其他记录。此外,它已被证明可以抵抗多种类型的攻击[9]。形式上,我们的定义提供了事件级 DP [10],如果每个人在数据集中只有一条记录,则相当于用户级。然而,为通用分析实施差异化私有机制仍然是一个公开的挑战[11]。尽管无法再从(乱序的)草图计算一些统计数据,但我们的机制仍然允许解决多个学习任务[1]。
4. 实现差异化隐私
我们现在正式证明,所提出的计算扰乱草图的本地和全局机制是有差别的私有的。


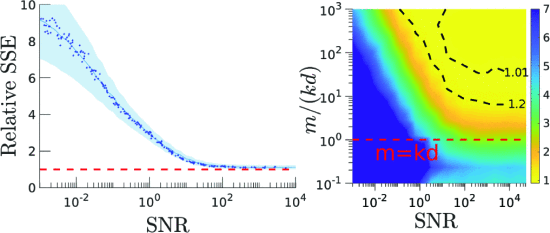
实用性的实验测量
定义了我们的机制并证明它实现了差异隐私后,我们现在展示噪声和屏蔽如何影响效用,为k均值定义为 SSE。为此,我们定义了平均草图的信噪比 (SNR),并通过实验证明 SSE 直接由该 SNR 和草图大小m 驱动。这些结果是针对任意噪声方差制定的σΨ2和掩蔽参数r。在第 6 节中,我们将使用第 4 节中的理论值来研究ε -DP 如何影响效用。


隐私与实用性的权衡
在本节中,我们研究第 4 节和第 5节分别提出的隐私保证和效用措施之间存在的权衡。当将获得-DP(命题1)所需的σ ψ值代入SNR(6)时,我们得到后者由ε和机构的其他参数参数化的表达式:
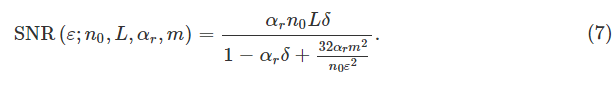
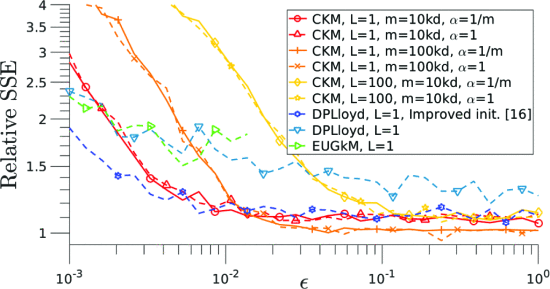
我们在图 3中显示了隐私-效用曲线,即相对 SSE 作为 ε 的函数,是针对n 0、L、α r和m的不同值获得的,并且我们使用 SNR ( 7 ) 的这个表达式来解释结果。
我们还将我们的方法与 DPLloyd [15](Lloyd 迭代算法的噪声变体)和 EUGkM [16](构建数据的噪声直方图)进行比较。DPLloyd 根据[17]在 matlab 中实现,按照作者的建议使用 5 次迭代。初始化要么统一执行,要么使用[16]中提出的方法执行。我们使用了作者的python EUGkM 实现1 ,以及建议的初始化。
当使用L = 1 设备(集中数据集)时,我们获得了良好的聚类结果,即相对 SSE 低于 1.2,前提是 ε>10 -2。参数α r不会对结果产生太大改变,因为子采样操作(即使用α r < 1)引起的方差项与( 7 )中的加性噪声引起的方差项相比较小。因此,我们可以自由地使用α r < 1 来降低计算成本,而不会降低实用性。与我们的方法相比,标准 DPLloyd 似乎表现不佳,但使用改进的初始化[16]确实有很大帮助。对于 EUGkM,由于算法基于直方图的性质,只能计算与较低 ε 值相对应的点,箱的数量变得很大;此类方法最适合中等大小的低维数据集。因此,我们得出的结论是,我们的方法至少与以前开发的方法一样好,同时需要较少的计算,具有受控的内存使用,并且可在分布式设置中使用。
相关工作
差分私有k均值已经在文献中受到关注。例如,拉普拉斯噪声的添加已在 SuLQ 框架[15]中使用,该框架提出了劳埃德迭代算法 (DPLloyd) 的噪声版本,或者在非交互式方法中使用,例如 EUGkM,它释放数据的噪声直方图[18],[16]。噪声水平有时会适应算法执行的实例,例如在样本和聚合方法中[13]。指数机制是选择用户定义的效用度量的输出概率的另一种标准方法,也已与遗传算法一起使用[19]。Feldman 等人对私有核心集进行了研究。[20]、[21]。流行的 k-means++ 播种方法也已推广到私有框架[22]。巴尔坎等人。使用基于 Johnson-Lindenstrauss 降维的方法研究了大规模高维设置[23]。已经提出了许多其他基于随机投影的嵌入作为数据的隐私保护编码,参见例如[24],通常假设对手不知道投影矩阵。
与我们的工作更接近的是,Balog 等人。最近提议发布内核均值嵌入[25],要么作为输入空间中的合成数据点集,要么使用特征图(就像我们所做的那样)。他们的工作依赖于高斯机制,导致差分隐私的定义较弱,附加项δ > 0。据我们所知,研究基于均值嵌入的机制的实用性是文献中的新内容。
结论
压缩数据集不仅减少了学习所需的资源,而且本质上有助于构建私有算法。我们提出了一种基于添加拉普拉斯噪声的草图方法,与子采样机制相结合以提高效率,该方法被证明是差分隐私的。
尽管我们专注于k均值聚类,但其他学习任务可以通过压缩方式解决,并且应该进行研究,例如高斯混合拟合或主成分分析。我们将使用量化草图[26](隐私量化已被考虑[27]、[28])并利用快速变换来加速过程[29]的想法留给未来的工作。在数据样本本身上使用加性噪声也是一种应该研究的可能性。