---

Outline

1. Motivation

2. Geometry

3. Algebraic manipulation

4. Observations

------------------------------

1. Motivation

Twin SVM的基本出发点是做二分类时，为什么我们只用1个分割超平面，为什么不能用两个呢？

这里是想用两个超平面来处理，一类点A围绕在超平面A旁边，一类点B围绕在超平面B旁边。得到两个non-parallel SVM hyperplane, 新来的点，离哪个超平面比较近，就属于哪一类。Twin SVM比较接近clustering的观念。

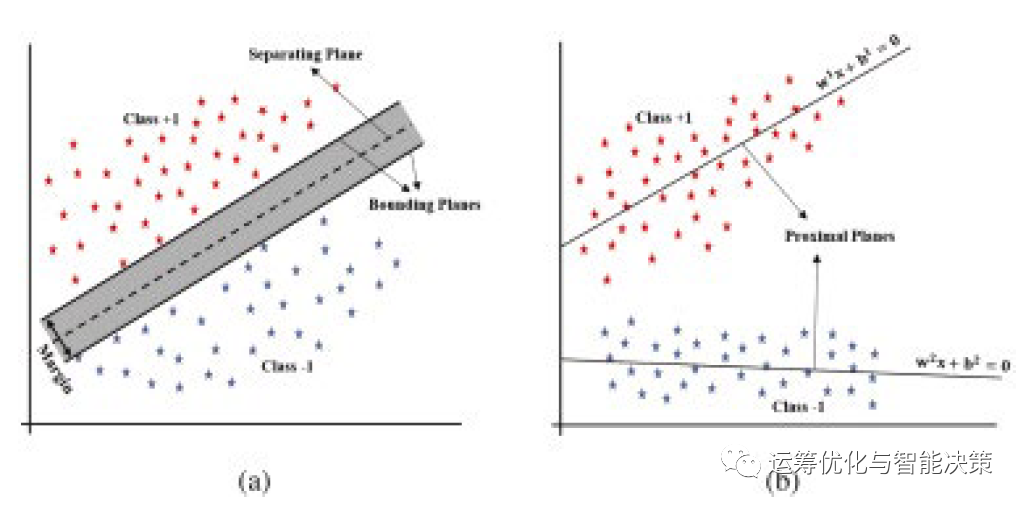
对比(a)与(b)的判断方式

• (a)是传统的SVM，新来一个点，要么在separation hyperplane上面，+1那一侧；要么在hyperplane的下面，-1那一侧。

• (b)是Twin SVM，新来一个点，either离hyperplane 1比较近，or 离hyperplane 2比较近。

------------------------------

从结论的角度来先说为什么要折腾Twin SVM

是因为Twin SVM的东西表现不比SVM差，而且计算快。虽然需要做两个SVM model, 但是每个SVM model的constraints要比传统的SVM少很多。从computational experiments上来看，效果不差，而且时间只要传统SVM的1/4 on average.

至于这个1/4是怎么的出来的，其实是计算复杂度理论，整个计算过程与约束条件数量的三次方有关。约束条件数量减半，就是1/8, 然后再乘2（两个SVM model），所以大体上就是的1/4耗时。

===================

2. Geometry 

这个图很明确，上面的蓝色小方块是一类，下面的红色小星号是一类。

更直观的理解，这个Twin SVM的东西就像两个管子tube.

一类在一个管子里，尽量聚集，越密越好；

另一类要在这根管子的外面，与这个管子保持足够的距离。

======================

3. Algebraic manipulation

==========================

4. Observations

-----------------------------

这里的TWSSVM是用来做二分类的，bi-classification的。

类似，LSSVM可以求dual，TWSSVM肯定也可以，求dual的procedure都是一样的。只是更加复杂一些而已。

-----------------------------

LSSVM当面对高度nonlinear的dataset时，可以变为KSSVM.

类似的，TWSSVM处理nonlinear dataset时，也可以升级成kernel-based TWSSVM.

甚至不升维时，TWSSVM也可以类比那些nonlinear的SVM的处理方式。

-----------------------------

学习一个东西，最重要的是思路，思路对了，站在道路上来看，每个方向都是通的。Twin的东西是另外一个思路，one separation hyperplane可以做的事情，twin的东西都可以做。