A. Rudolph and Cut the RopeA. Rudolph and Cut the Rope

题目大意

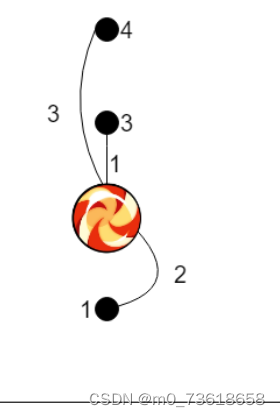
有 n 个钉子钉在墙上，第 i 个钉子被钉在离地面 ai 米高的位置，一根长度为 bi 米的绳子的一端被绑在它上面。所有钉子都悬挂在不同的高度上。糖果同时被绑在所有绳子的末端，而这些绳子又没有被绑在任何一个钉子上。
为了拿到糖果，你需要将它放到地面上。为了做到这一点，Rudolph 可以一次剪断一根绳子。帮助 Rudolph 找出至少需要剪断多少根绳子才能获得糖果。
在这里插入图片描述

思路分析

为了使糖果能够落到地上，需要所有的绳子都触及地面。这意味着所有绳子的长度必须大于或等于它们所连接的钉子的高度。也就是说，需要剪断那些长度小于其所连接钉子高度的绳子。然后答案就等于满足ai>bi的元素数量。

时间复杂度

O(n)

题解代码

#include <iostream>

using namespace std;


int main() {
	int test_cases;
	cin >> test_cases;

	for (int test_case = 0; test_case < test_cases; test_case++) {
		int n;
		cin >> n;
		int ans = 0;
		for (int i = 0; i < n; i++) {
			int a, b;
			cin >> a >> b;
			if (a > b)
				ans++;
		}
		cout << ans << endl;
	}

	return 0;
}

B. Rudolph and Tic-Tac-Toe

题目大意
Rudolph 发明了一个三人玩的井字游戏。它具有经典规则，但第三个玩家使用加号。Rudolph 有一个 3×3 的场地，代表已完成的游戏结果。每个方格中可能包含叉、圈、加号、或者为空。游戏的目标是使任意一名玩家以其符号在水平、垂直或对角线方向上连成三个。
Rudolph 想要找出游戏的结果。结果可能是仅有一名玩家赢得了比赛，或者是平局。确保不会有多名玩家同时获胜。
输入
第一行包含一个整数 t(t≥1，t≤104) - 测试案例的数量。
每个测试案例由三行组成，每行包含三个字符。符号可以是四种之一：“X” 表示叉，“O” 表示圈，“+” 表示加号，“.” 表示空白格子。
输出
对于每个测试案例，打印字符串 “X” 如果叉获胜，“O” 如果圈获胜，“+” 如果加号获胜，“DRAW” 如果平局。

思路分析

只需要检查每行、每列和每条对角线的三个元素是否相等。如果所有三个元素都相等且不为".“，则这些元素的值就是答案。需要注意的是，连续三个为空白格子(”.“)并不会给出答案”."。题目没有规定玩家走棋的次数相同，这意味着一个玩家可能会有多个获胜的行

时间复杂度

O(1)

题解代码

#include <iostream>
#include <vector>
#include <string>


using namespace std;

int main() {
	int test_cases;
	cin >> test_cases;
	for (int test_case = 0; test_case < test_cases; test_case++) {
		vector<string> v(3);
		for (int i = 0; i < 3; i++)
			cin >> v[i];
		string ans = "DRAW";
		for(int i = 0; i < 3; i++) {
			if (v[i][0] == v[i][1] && v[i][1] == v[i][2] && v[i][0] != '.')
				ans=v[i][0];
		}
		for (int i = 0; i < 3; i++) {
			if (v[0][i] == v[1][i] && v[1][i] == v[2][i] && v[0][i] != '.')
				ans=v[0][i];
		}
		if (v[0][0] == v[1][1] && v[1][1] == v[2][2] && v[0][0] != '.')
			ans=v[0][0];
		if (v[0][2] == v[1][1] && v[1][1] == v[2][0] && v[0][2] != '.')
			ans=v[0][2];
		cout << ans << endl;
	}
	return 0;
}

C. Rudolf and the Another Competition

题目
Rudolf报名参加了一场遵循ICPC规则的编程竞赛。根据规则，每解决一个问题，参赛者将获得11分，并且会承担从比赛开始到解决问题的时间所对应的罚时。在最终的排行榜中，分数最高的参赛者排名靠前，如果分数相同，则罚时较低的参赛者排名靠前。
总共有n个参赛者报名参加比赛。Rudolf的索引为1。已知将提出m个问题。比赛将持续h分钟。
一款强大的人工智能预测了ti,j的值，表示第i个参赛者解决第j个问题需要的时间。Rudolf意识到解决问题的顺序会影响最终的结果。例如，如果h=120，并且解决问题的时间是[20,15,110]，那么如果Rudolf按照以下顺序解决问题：
3,1,2，那么他只能解决第三个问题，获得11分和110的罚时。
1,2,3，那么他将在比赛开始后20分钟解决第一个问题，在20+15=35分钟后解决第二个问题，而没有时间解决第三个问题。因此，他将获得22分和55的罚时。
2,1,3，那么他将在比赛开始后15分钟解决第二个问题，在15+20=35分钟后解决第一个问题，而没有时间解决第三个问题。因此，他将获得22分和50的罚时。
Rudolf想知道如果每个参赛者按照人工智能的预测以最优顺序解决问题，他将在比赛中获得的名次。假设如果分数和罚时相同，Rudolf将获得最好的名次。

思路分析

时间复杂度

O(t * m * (m + log m))。

代码

#include <bits/stdc++.h> 
#define int long long 

using namespace std;

signed main() {  
    ios::sync_with_stdio(false);  // 关闭输入输出流同步，提高输入输出效率
    cin.tie(nullptr);  // 解除 cin 与 cout 的绑定
    cout.tie(nullptr);
    int t; 
    cin >> t;  
    while(t--){ 
        int n, m, h;  
        cin >> n >> m >> h; 
        pair<int, long long> rud;  // 创建一个 pair 对象 rud，存储问题数量和罚时
        int ans = 1;  // 初始化答案 ans 为 1
        for(int i = 0; i < n; i++){  
            vector<int> cur(m);  
            for(int j = 0; j < m; j++){  
                cin >> cur[j];  
            }
            std::sort(cur.begin(), cur.end());  // 对 cur 进行升序排序
            int task_cnt = 0;  task_cnt 为 0
            long long penalty = 0, sum = 0;
            for(int j = 0; j < m; j++){ 
                if (sum + cur[j] > h) break; 
                sum += cur[j]; 
                penalty += sum; 
                task_cnt++; 
            }
            if (i)
            { 
                if (make_pair(-task_cnt, penalty) < rud) ans++;  
            } else rud = {-task_cnt, penalty};  // 更新 rud 的值为当前问题数量和罚时的负数
        }
        cout << ans << '\n'; 
    }
    return 0;  
}