A小红的基环树

题目描述
定义基环树为n个节点、n条边的、没有自环和重边的无向连通图。
定义一个图的直径是任意两点最短路的最大值。
小红想知道，n个节点构成的所有基环树中，最小的直径是多少？

思路分析

特判n=3时为1，其他时候都为2

知识点

定义一个图的直径是任意两点最短路的最大值。

时间复杂度

O(1)

代码

#include<iostream>
using namespace std;

int main() {
    int n;
    cin >> n;
    
    if (n == 3) {
        cout << 1 << endl;
    } else {
        cout << 2 << endl;
    }
    
    return 0;
}

B小红的回文串

思路分析

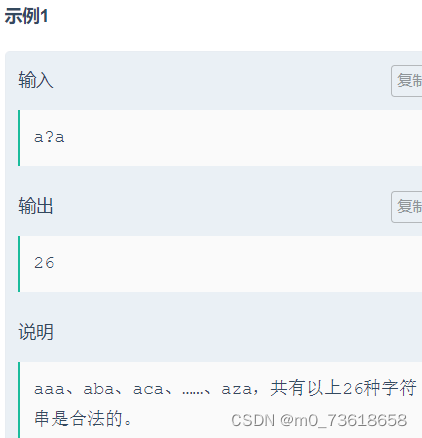
遍历字符串的前半部分，从左右两边向中间比较对应位置的字符。如果两个字符都是’?‘，则可以选择26种不同的字母进行替换；如果两个字符相同，则无需替换；如果两个字符不同，则无法构成回文串，方案数为0。需要注意的是，如果字符串长度为奇数且中间字符是’?'，则也可以选择26种不同的字母进行替换。
根据上述判断条件，累乘合法方案数，并对结果取模。

时间复杂度

O(n/2)

代码

#include<iostream>
#include<string>
using namespace std;
const long long mod = 1e9 + 7;

int main() {
    string s;
    cin >> s;
    int n = s.length();
    
    long long ans = 1;
    for (int i = 0; i < n / 2; i++) {
        char c1 = s[i];
        char c2 = s[n - i - 1];
        
        if (c1 == '?' && c2 == '?') {
            ans = (ans * 26) % mod;
        } else if (c1 != '?' && c2 != '?' && c1 != c2) {
            ans = 0;
            break;
        }
    }
    
    if (n % 2 == 1 && s[n / 2] == '?') {
        ans = (ans * 26) % mod;
    }
    
    cout << ans << endl;
    
    return 0;
}

C小红的数组操作(easy version)

题目大意

给定一个数组，通过对数组中的元素进行增减操作，使得操作后的数组的平均数成为整数。要求找出最小的总代价。

思路分析

读取输入的数组大小N、操作费用P、增加量X、操作费用Q、减少量Y以及数组元素。
计算数组元素之和sum，并对sum取模N，得到余数。
初始化最小代价ans为一个较大的值1e18。
遍历从0到N的每一个位置i：
计算当前方案的总代价cost，根据给定的公式计算：iQ + (N - ((sum - iY) % N + N) % N) % N * P。
更新最小代价ans为cost和ans中的较小值。

时间复杂度

O(N)

代码

#include <iostream>
#include <vector>
using namespace std;

void solve() {
    int N, P, X, Q, Y;
    cin >> N >> P >> X >> Q >> Y;
    vector<int> a(N + 1);
    int sum = 0;
    for (int i = 1; i <= N; i++) {
        cin >> a[i];
        sum += a[i];
    }
    sum %= N;
    int ans = -1;
    for (int i = 0; i <= N; i++) {
        ans = min(ans, i * Q + (N - ((sum - i * Y) % N + N) % N) % N * P);
    }
    cout << ans << "\n";
}

int main() {
   solve();
    return 0;
}