文章目录
- 前言:符号位、原码、补码、反码
- 1.是什么
- 2.各种码转换
- 一.二进制高低位
- 1.1.什么是高低位
- 1.2.高低位交换
- 二.位逻辑运算符
- 位与运算 &
- 位或运算 |
- 异或运算 ^
- 取反运算 ~
- 三.位移运算符
- 左位移运算符 <<
- 右位移运算符 >>
- 1.正数右移:
- 2.负数右移(带符号右移)
- 3.无符号右移>>>
- 四.复合位赋值运算符
- 五.总结
前言:符号位、原码、补码、反码
1.是什么
首先 我们看到的数,都是以二进制的形式在计算机下操作的。并且位运算符的操作对象是补码。
符号位 :如8位数,左边第一位是符号位,剩余7位表示数据大小(
1为负,0为正)
正数: 原码=反码=补码
负数: 原码 ---->反码 (取反) ---->补码 (+1)
- 原码:将一个整数,转换成
二进制,就是其原码。 - 反码:正数的反码就是其原码;
负数的反码是将原码中,除符号位以外,每一位取反。 - 补码:正数的补码就是其原码;
负数的反码+1就是补码
2.各种码转换
1.负数原码转反码
- 符号位不变,数值位按位取反。
原码:1(符号位不变)000 1100 反码:1(符号位不变)111 0011
2.负数原码转补码的
-
先转换为反码(符号位不变,数值位按位取反)
-
在反码的基础上末位加一
原码:1(符号位不变)010 0101 反码:1101 1010 补码:1101 1011
3.负数原码转补码的
- 符号位不变,数值位按位取反,末位加一
补码: 1110 1011 补码取反: 1001 0100 原码: 1001 0101
4.负数反码相互补码
- 负数的反码转换为补码:末位加一
java 反码:1100 1110 补码:1100 1111
负数的补码转换为反码(源码的反码):末位减一补码:1100 1110 反码:1100 1101 (借位减)
5.正数取反
- 先将正数原码按位取反,得到一个负数,由于负数以补码形式存在,再转换为负数的反码,最后末位加一得到补码。
0000 1100 #原码
1111 0011 #正数取反得到负数的原码
1000 1100 #负数的原码取反后得到反码
1000 1101 #反码加一得到补码
一.二进制高低位
1.1.什么是高低位
二进制是一种数字编码方式,由0和1两个数字组成。在二进制中,每一位都有一定的权值,从右往左依次为1、2、4、8、16、32、64、128...依次递增(都是2的整数倍)。
- 最右边的第1位称为
二进制的低位,第2位称为次低位,以此类推,第n位称为第n-1 位。 - 最左边的第1位称为
二进制的高位。
举个例子,二进制数 10110的低位是 0,次低位是1,第3位是1,第4位是0,第5位是1,因此它的高位是1。
- 如果用内存中的2个字节表示一个
16位的数,那么其中的一个字节将存放最低的8位有效位,而另一个字节将存放最高的8位有效位。如图所示。 - 通俗一点讲,就是从左向右,越左位权越高

1.2.高低位交换
x= 10000110 11011000
称这个二进制数的前8位为“高位”,后8位为“低位”。现在写一程序将它的高低位交换。
- x执行右移 8 位,右移时会执行逻辑右移即高位补0,因此x右移8位将得到
00000000 10000110 - x左移8位将得到
11011000 00000000 - 两者 在
|就的实现了交换
00000000 10000110
11011000 00000000
//当相同位上的数字至少有一个为1时,结果为1 最终结果实现高低位呼唤
11011000 10000110
a = (a >> 8) | (a << 8);
二.位逻辑运算符
位逻辑运算符包含 4 个:&(与)、|(或)、~(非)和 ^(异或)。除了 ~(即位取反)为单目运算符外,其余都为双目运算符。
位与运算 &
- 按二进制形式,低位对齐,高位不足的补零。
当相同位上的两个数字都为1时,结果为1;否则为0

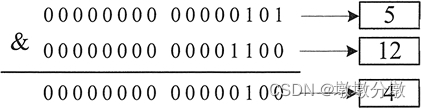 ``
``
位或运算 |
- 按二进制形式,低位对齐,高位不足的补零
。当相同位上的数字至少有一个为1时,结果为1;否则为0
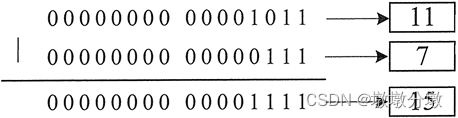
异或运算 ^
- 按二进制形式,低位对齐,高位不足的补零,
当相同位上的两个数字不同时,结果为1;相同时为0

取反运算 ~
- 当相同位上的为1时结果为0,反之。相同位上的为0时结果为1

三.位移运算符
左位移运算符 <<
按二进制形式把所有的数字向左移动对应的位数,高位舍弃,低位的空位补零。即:将二进制数字向左移动,移动几位就在最右侧补多少个0。
11 << 1 =22

- 原来数的所有二进制位都向左移动 1 位。原来位于左边的
最高位 0 被舍弃,再向尾部追加 0 补位。最终到的结果是 22,相当于原来数的 2 倍。- 左移n位相当于乘以2的n次方
- 11 << 1 等于
11x2的1次方 等于 22、11 << 2 等于11x2的2次方 等于 44
- 11 << 1 等于
- 左移n位相当于乘以2的n次方
右位移运算符 >>
1.正数右移:
按二进制形式把所有的数字向右移动对应的位数,低位舍弃,高位的空位补零。即:将二进制数字向右移动,移动几位就在最左侧补多少个0。
11 >> 1 = 5
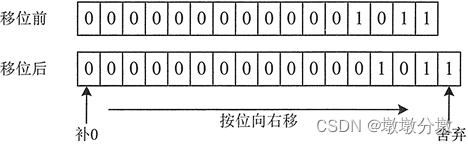
- 原来数的所有二进制位都向右移动 1 位。原来位于右边的
最低位 1被移出舍弃,再向最高位追加 0 补位。最终到的结果是 5,相当于原数整除 2 的结果。- 正数右移n位相当于原数除2的n次方
- 11 >> 1 等于
11/1的2次方取整等于6、11 >> 2 等于11/2的2次方4取整等于2
- 11 >> 1 等于
- 正数右移n位相当于原数除2的n次方
2.负数右移(带符号右移)
高位补1,等价于对绝对值除以2的n次方,再加上负号
-100 >>4 : -100带符号右移4位 =等于100/16
-100原码:
10000000 00000000 00000000 01100100
1. -100补码: 保证符号位不变,其余位置取反加1
11111111 11111111 11111111 10011100
2. 右移4位: 在高位补1(11111111 11111111 11111111 1001高位补4个1)
补码形式的移位完成后,结果不是移位后的结果,要根据补码写出原码才是我们所求的结果。其方法如下:
3.保留符号位,然后按位取反
11111111 11111111 11111111 11111001
//按位取反
10000000 00000000 00000000 00000110
4.然后加1,即为所求数的原码:
10000000 00000000 00000000 00000110
//+1
10000000 00000000 00000000 00000111
结果为:-7
3.无符号右移>>>
不考虑符号位,统一补0,用于移动无符号数,不会改变符号位的值,等价于对无符号数除以2的n次方。
-100 >>>4
-100原码: 10000000 00000000 00000000 01100100
1. -100补码:保证符号位不变,其余位置按位取反加1
10000000 00000000 00000000 01100100
11111111 11111111 11111111 10011100
2.无符号右移4位 :: 在高位补0
11111111 11111111 11111111 10011100
00001111 11111111 11111111 11111001
即为所求:268435449
四.复合位赋值运算符
- &= 按位与赋值 num1 &= num2 等价于 num 1=num 1 & num2
- |= 按位或赋值 num1 |= num2 等价于 num 1=num 1 | num2
- ^= 按位异或赋值 num1 ^= num2 等价于 num 1=num 1 ^ num2
- -= 按位取反赋值 num1 -= num2 等价于 num 1=num 1 - num2
- «= 按位左移赋值 num1 «= num2 等价于 num 1=num 1 « num2
- »= 按位右移赋值 num1 »= num2 等价于 num 1=num 1 » num2
五.总结
-
正数的左移与右移,负数的无符号右移,就是相应的
补码移位所得,在高位补0即可。 -
负数的右移,就是
补码高位补1,然后按位取反加1即可。