内容：二叉树的前、中，后序遍历，层序遍历，二叉树节点个数，叶子节点个数，二叉树高度，第k层节点的个数，查找某个节点，二叉树销毁，判断是否为完全二叉树

目录

 前序遍历：

中序遍历：

后序遍历：

层次遍历：需要借助队列

 二叉树节点个数：

 二叉树叶子节点的个数：

二叉树的高度：

二叉树第k层的节点个数：

查找某个节点并返回其地址：

二叉树销毁：

判断是否为完全二叉树：借助队列

---

事前准备：

typedef int BTDataType;
typedef struct BinaryTreeNode//二叉树节点
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode*right;
}BTNode;

BTNode* BuyNode(BTDataType x)//创建一个节点
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;
	return node;
}

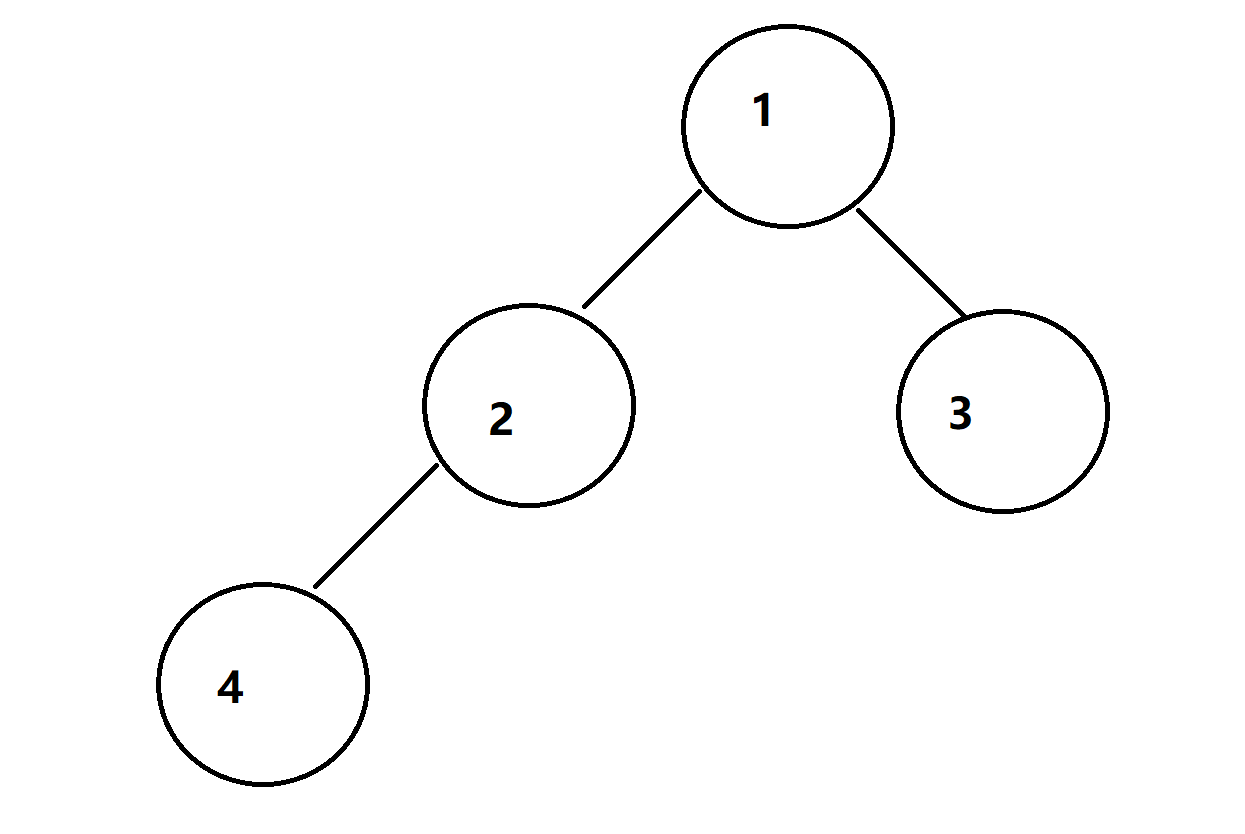
手动构造一个二叉树，用以验证：图示如下

BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);

	node1->left = node2;
	node1->right = node3;
	node2->left = node4;

	return node1;
}

 前序遍历：

void PrevOrder(BTNode* root)
{
	if (root == NULL)//进入一个空树
	{
		printf("N ");
		return;
	}

	printf("%d ", root->data);//访问根节点的值
	PrevOrder(root->left);//访问左子树
	PrevOrder(root->right);//访问右子树
}

  

中序遍历：

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	InOrder(root->left);//访问左子树
	printf("%d ", root->data);//访问根节点
	InOrder(root->right);//访问右子树
}

 

后序遍历：

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	PostOrder(root->left);//访问左子树
	PostOrder(root->right);//访问右子树
	printf("%d ", root->data);//访问根节点
}

层次遍历：需要借助队列

借助队列先进先出的性质，一个节点出队，带入它不为空的左右孩子入队

相关队列功能的所需函数及队列结构的定义：

typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode//队列中的节点
{
	QDataType data;
	struct QueueNode* next;
}QNode;

typedef struct Queue//队列
{
	QNode* phead;//指向队头的指针
	QNode* ptail;//指向队尾的指针
	int size;
}Queue;

void QueueInit(Queue* pq);//初始化
void QueueDestroy(Queue* pq);//销毁
void QueuePush(Queue* pq, QDataType x);//插入
void QueuePop(Queue* pq);//删除
QDataType QueueFront(Queue* pq);//获取队头元素
bool QueueEmpty(Queue* pq);//判空

 

void QueueInit(Queue* pq)
{
	assert(pq);//断言，pq一定不为空
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
}

void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->phead;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}

	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}

void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		return;
	}
	newnode->data = x;
	newnode->next = NULL;

	if (pq->ptail == NULL)//第一次插入，链表中没有节点
	{
		assert(pq->phead == NULL);
		pq->phead = pq->ptail = newnode;
	}
	else//尾插
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}
	pq->size++;
}

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	if (pq->phead->next == NULL)//链表中仅有一个节点
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;
	}
	else//多个节点，头删
	{
		QNode* next = pq->phead->next;
		free(pq->phead);
		pq->phead = next;
	}
	pq->size--;
}

QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->phead->data;
}


bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->size == 0;
}

层序遍历：

void LeverOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);

	if (root)//将根节点入队
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))//一个节点出队，带入它的左右孩子
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);

		if (front->left)//左孩子不为空，入队
		{
			QueuePush(&q, front->left);
		}

		if (front->right)//右孩子不为空，入队
		{
			QueuePush(&q, front->right);
		}
	}

	printf("\n");
	QueueDestroy(&q);
}

 二叉树节点个数：

空树返回0 

非空树返回：左子树节点的个数+右子树节点的个数+1

int BTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BTreeSize(root->left)
		                    + BTreeSize(root->right) + 1;
}

 二叉树叶子节点的个数：

进入一个空树返回0

非空树：若本身是叶子，返回1，否则返回左子树叶子的个数+右子树叶子的个数

int BTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	if (root->left == NULL && root->right == NULL)//本身是叶子
	{
		return 1;
	}

	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);//非叶子
}

二叉树的高度：

 进入一个空树，返回0

非空树：找出左右子树高度更高的一个，返回其+1

int BTreeHeight(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	int leftHeight = BTreeHeight(root->left);
	int rightHeight = BTreeHeight(root->right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

二叉树第k层的节点个数：

 进入空树，返回0

非空树：若它的k==1，则求的就是它这一层，返回1

              否则，返回它左子树第k-1层的节点个数+右子树第k-1层的节点个数

int BTreeLevelKSize(BTNode* root,int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}

	if (k == 1)
	{
		return 1;
	}

	return BTreeLevelKSize(root->left, k - 1)
		+ BTreeLevelKSize(root->right, k - 1);
}

如求其第2层的节点个数：

查找某个节点并返回其地址：

BTNode* BTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}

	if (root->data == x)//根节点就是，直接返回
	{
		return root;
	}

	BTNode* ret1 = BTreeFind(root->left, x);//去左子树找
	if (ret1)//找到了，返回
	{
		return ret1;
	}

	BTNode* ret2 = BTreeFind(root->right, x);//去右子树找
	if (ret2)//找到了，返回
	{
		return ret2;
	}

	return NULL;//根，左子树，右子树全都找不到，返回NULL
}

二叉树销毁：

void BTreeDestroy(BTNode* root)
{
	if (root == NULL)//进入空树，返回
	{
		return;
	}

	BTreeDestroy(root->left);//销毁左子树
	BTreeDestroy(root->right);//销毁右子树
	free(root);//销毁根节点
}

判断是否为完全二叉树：借助队列

一个节点出队，让它的左右孩子进队，不管左右孩子是否为空

若是完全·二叉树，则出到第一个NULL时，这个NULL后面的所有队列元素都是NULL

若不是完全二叉树，则出到第一个NULL时，这个NULL后面的所有队列元素中有元素不是NULL

bool BTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);

	if (root)//根节点入队
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))//出队列元素
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)//出到第一个NULL，结束循环，进行判断它后面的所有处在队列中的元素是否都为NULL
		{
			break;
		}

		QueuePush(&q, front->left);//不管是否为空，左右孩子都进队
		QueuePush(&q, front->right);
	}

	while (!QueueEmpty(&q))//判断第一个NULL出队后，队中所有元素的情况
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front)//如果队中有非空节点，则不是完全二叉树
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;//第一个NULL出队后，队中所有元素均为NULL
}

完结撒花~