一、阴影

• 判断一个点是否被遮住，可以从该点像光源方向发射射线（P + tL），若射线被与物体发生相交，则说明它在阴影中。而这个物体由于要在 P 和 光源之间，在方向光场景下， t 的取值范围是 0 < t < +∞（因为光源无限远），而在点光下， t 的取值范围是 0 < t < 1。

二、光栅化三角形

光追的简单性的代价是性能。而光栅化渲染模型是追求性能，而不是数学纯度。它的思维方式和光追相反。

• 光追：思考画布上的每个像素，场景中的哪个物体在这里是可见的？

• 光栅化：思考场景中的物体，在画布上的哪个像素这个物体是可见的？

• 绘制任意斜率的直线
  当线趋于水平时（abs(dx) > abs(dy)）使用 y = f(x) ，确保能画出水平线
  当线趋于垂直时（abs(dy) > abs(dx)）使用 x = f(y) ，确保能画出垂直线

• 线性插值函数
  是基于绘制任意斜率中提取的公共部分，为 Interpolate() ，它计算两点之间线段上的点的 x 或 y 值，放置到一个数组中。当线趋于水平时，使用 Interpolate(x0,y0, x1,y1) 返回这些值是 y（因变量），当线趋于垂直时，使用Interpolate(y0,x0, y1,x1) 返回的这些值是 x
  这并不是最好的算法，目前比较好的直线算法是布兰森汉姆算法

• 三角形的绘制方式
  给定三角形， 找出长边和短边，通过长边和两条短边的 x 坐标并集，找出左边的边和右边的边，自底向上从左边的点绘制到右边的点

• 三角形的边缘着色
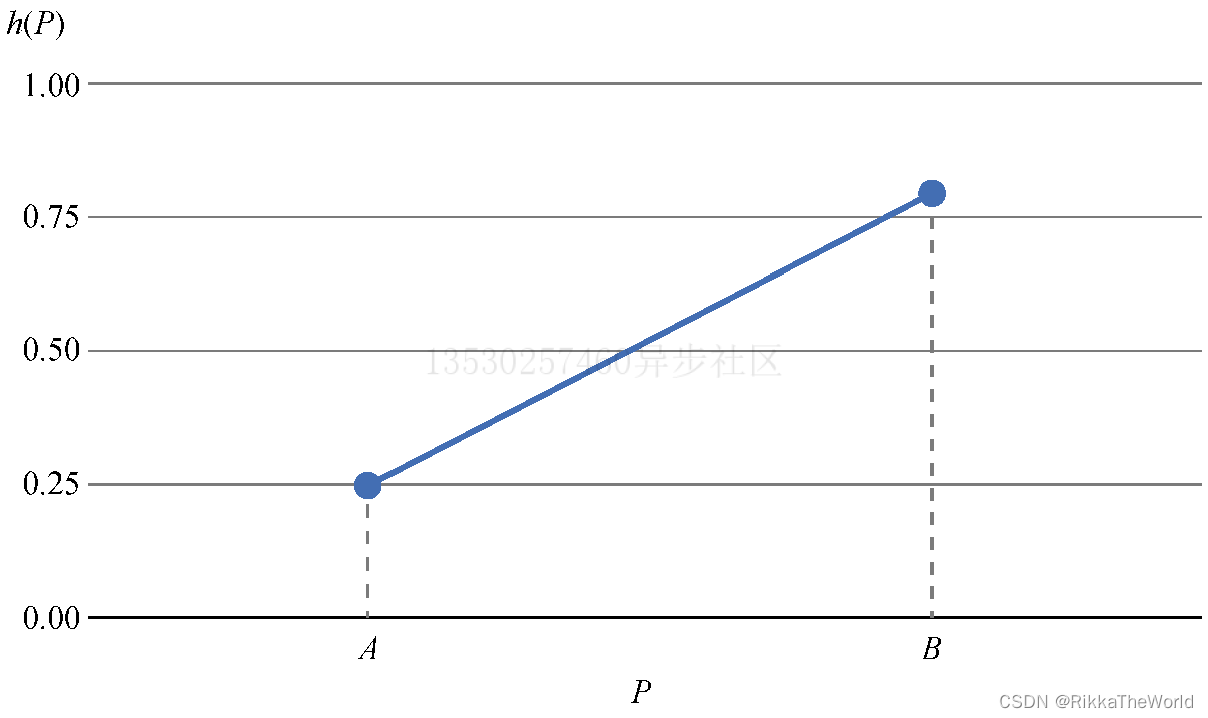
  三角形颜色基色为 C，已知三个顶点的颜色强度为 h（取值范围为 [0,1]，0表示黑色，1表示原色），那么每个点的颜色为 Ch = (Rc h, Gc h, Bc h)
  其次，边缘两点之间的点的颜色，可以用 h = f(P) 来计算，但是我们不知道它们的关系，所以可以先悬着一条兼容的函数，如下面的线性函数。
  和三角形绘制的方式一样，我们通过线性插值函数，来计算每条边的上 h 的取值范围：
  h01 = Interpolate(y0,h0, y1,h1) h12 = Interpolate(y1,h1, y2,h2) h02 = Interpolate(y0,h0, y2,h2)
  然后跟随 x 取值找出每个水平线上的最左值和最右值
  

• 三角形内部着色
  在获取到条水平线上的 hl 和 hr 之后，我们可以通过 xl 和 xr，来使用线性插值器计算这个线段上每个点的 h 值，这样就可以获取到每个像素的颜色了

三、 透视投影

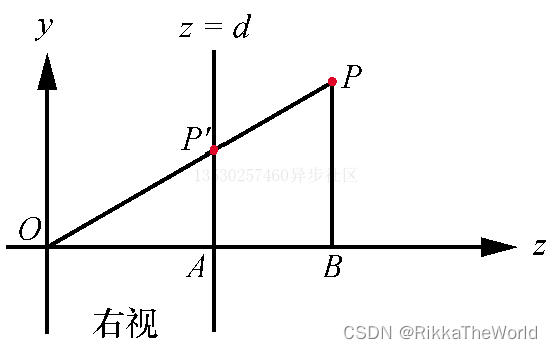
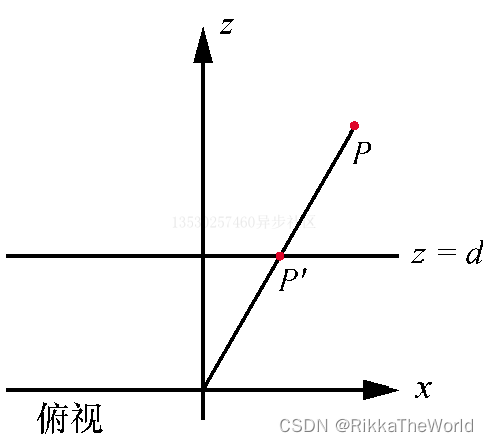
• 查找视口上的 P’ 点
  通过右视，可以用相似三角形的方法，确定 P'y = Py·d / Pz
  通过俯视，确定 P'z = Px·d / Pz
  
• 透视投影方程
  将上述整合在一起，给定场景中的一个点 P 以及相机位置和视口的设置，我们可以计算 P 在视口上的投影，我们称之为 P’，那么 P’ 的坐标就是 (Px·d/Pz， Py·d/Pz， d)，在前面章节中学习了 画布 - 视口转化方程，这里需要反过来，编程 视口 - 画布转化方程，因此视口上 P’ 对应的 画布坐标为：

// Cw、Ch 为画布长宽， Vw Vh 为视口长宽
Cx = P'x · Cw / Vw
Cy = P'y · Ch / Vh

• 表示一个立方体
  一个立方体可以看出是 8 个顶点，组成的 12 个三角形，因此可以使用绘制三角形的方式来绘制一个立方体。从而实现二维到三维的转化
• 模型变换
  可以使用三个元素来定义模型变化，分别是：缩放、旋转、平移，无论是先平移后旋转，还是旋转后平移，都可以达成一样的效果，而在计算中，我们采用：先缩放，后旋转，最后平移 来计算模型最后的形态。
  在固定场景中旋转和平移相机，与固定相机而旋转和平移场景是没有区别的。但是如如果固定相机，并指向 Z+，我们的透视投影方程就不用做出任何修改。这种坐标系也被称为相机空间。
  假设相机也附加了变化，包括平移、旋转，为了从相机的视野去渲染场景，我们需要对场景中的每个顶点应用相反的变化，计算如下：

Vtranslated = Vscene - camera.translation    // 世界平移程度（每个坐标的移动距离） = 每个场景的坐标 - 相机的平移距离
Vcam_space = inverse(camera.roation) · Vtranslated    // 相机的位置 = 旋转后平移位置， 这里的旋转角度是相机本身的旋转角度的相反数
Vprojected = perspective_projection(Vcam_space)    // 此时可以使用投影透视方程，算出场景中每个物体在平面上的坐标

• 变换矩阵
  现在考虑在移动相机时，模型空间中的顶点 Vmodel 所发生的事情，直到它被投影到画布点 (cx， cy）。我们首先应用模型从模型空间到世界空间：

Vmodel_scaled = instance.scale · Vmodel  // 模型缩放后的模型 = 实例的缩放因子 * 模型原始大小
Vmodel_roated = instance.roation · Vmodel_scaled  // 模型旋转后的模型 = 实例的旋转因子 * 模型缩放后的模型
Vworld = Vmodel_rotated + instance.translation   // 世界空间的每个点 = 模型旋转后的模型 + 实例的平移距离

然后应用相机变化，从世界空间变换到相机空间：

Vtranslated = Vworld - camera.translation                  // 世界平移坐标 = 世界原位置 - 相机移动位置
Vcamera = inverse(camera.roation) · Vtranslated      // 相机位置 = 相机反方向旋转然后平移 

接下来，应用透视方程获得视口坐标：

vx = Vcamera.x · d / Vcamera.z
vy = Vcamera.y · d / Vcamera.z

最后将视口坐标映射到画布坐标：

cx = vx · cw / vw
cy = vy ·  ch / vh

下面来简化这个方程，函数的输入是场景中的任意顶点，返回的是变化之后的顶点位置。设 Ct、Cr 为相机平移函数和旋转函数，IR、IS、IT 为模型实例的旋转函数、缩放函数、平移函数，P 为透视投影函数，M为视口-画布转换函数。V 表示原始顶点位置，V’ 表示画布上的坐标，我们可以使用下面这样表示以上所有方程：

V' = M(P(CR%^-1(CT^-1(IT(IR(IS(V)))))))        // 新顶点坐标 = 模型上的原始坐标被缩放、旋转、平移后，再经过被相机自身平移、缩放，被投影到视口上，再转化到画布上
F = M · P ·CR^-1 · CT^-1 · IT ·IR · IS     // 定义函数
V' = F(V)

• 齐次坐标
  由于 A = （x, y, z） 可以表示为一个点（笛卡尔坐标系），也可以表示为一个向量，因此为了更好的区分它们，我们引入 w 值，w = 0 时表示它为向量，w = 1时表示它为点， 我们称 A=（x,y, z, w） 为齐次坐标 。 处理齐次坐标与处理向量是一致的，例如：

(8, 4, 2, 1) - (3, 2, 1, 1) = (5, 2, 1, 0)

当 w 既不为0 也不为1时，它依然表示点，而 w 则是坐标个 w 值之间的比率，例如 (1,2,3,1) 和 (2,4,6,2) 表示的是同一个点，我们可以使用下面公式，将齐次坐标转化为笛卡尔坐标

(x, y , z , w) = (x/w, y/w, z/w, 1) = (x/w, y/w, z/w)